山区低等级公路弯坡组合路段安全性仿真
2022-03-16王宪彬陈思远
王宪彬,陈思远
(东北林业大学 交通学院,哈尔滨 150040)
山区公路的线形设计往往受到地理环境的限制,尤其是在山区低等级公路的弯坡组合路段,由于地形复杂,车速控制较难,经常出现汽车失控问题,进而引发事故。目前,国内外关于山区公路弯坡组合路段的安全性研究主要分为以下3类:
一是从汽车行驶稳定性入手,以不同条件为基础建立弯坡组合路段安全模型,分析汽车在行驶中的稳定状态与道路设计安全性的相关性。Glaser等[1]通过分析汽车纵向和横向动力学极限,设计了一种汽车转弯时的道路偏离报警装置。Shin等[2]建立了以汽车不发生侧滑和侧翻为约束条件的弯道安全评价方法,并设计了不同弯道的安全半径。Himers等[3]通过建立基于侧滑稳定性的可靠度评价模型,得到不同设计速度和超高下的弯道最小安全半径。Easa等[4]用计算机模拟了竖曲线对最小安全半径的影响,并用其建立了设计半径所需的数学模型。王芊[5]选取汽车稳态侧向加速度和稳态车身侧倾角为指标,运用Carsim软件进行仿真,并评价了不同情况下的汽车转向对汽车操纵稳定性的影响。杨俊儒等[6]建立了更高精度的汽车在不同因素影响下弯道行驶时失稳的临界车速计算模型。阎莹等[7]利用TruckSim进行仿真,得到了不同弯坡组合路段重载车的失稳临界车速。Tian等[8]利用TruckSim建立三维道路模型和力学模型,分析了大客车在弯道段侧滑和侧翻的关键参数和指标。岳雷等[9]以事故临界状态为限制,计算了汽车实际运行车速下的弯坡组合路段设计指标阈值。
二是从驾驶员角度进行数据调查及分析,通过大量试验建立人-车-路协同仿真,研究驾驶员的实际反应数据与道路设计指标安全性之间是否存在规律。如Lusetti等[10]设计出了一种通过综合计算临界安全速度来控制汽车在坡道转弯时速的模型。Guo等[11]基于对不同道路半径和坡度的驾驶员反应轨迹研究,建立了基于垂直和水平曲线组合的轨迹预测模型。胡立伟等[12]通过实际道路数据,采集心率变异性来表征驾驶负荷,并通过建模仿真确定事故多发路段与弯坡组合道路数据之间的规律。王宏鹏等[13]通过建模仿真定量分析了驾驶员的驾驶负荷与公路弯坡路段数据之间的变化关系。Shi等[14]分析了平曲线半径、坡度和视距三者与运行速度的关系,构建了关于视距和各线形要素的运行速度预测模型。万远航[15]通过构建人-车-路协同仿真系统,研究了不同驾驶模式下汽车在山区坡路的行驶特性。
三是以现有道路线形为基础,对其采集的道路数据进行模型设计、仿真及计算,从不同角度得到更安全的线形设计方法。Bucchi等[16]在以纵坡和弯坡路段为对象的运行速度预测模型中引入超高和坡度角,对其进行道路安全性研究。Ambrož等[17]设计了收集路面数据而形成的3D模型系统,可用于模拟驾驶动力学。Rusdi等[18]通过收集马来西亚山区公路数据,采用了多种建模技术,计算了车辆事故和山区公路线形之间的函数关系。Varunjikar[19]通过建立不同车辆计算模型,对特殊路段弯坡组合线形进行分析,得出安全合理的弯坡组合形式。刘姣[20]利用八自由度驾驶模拟器实验采集了汽车在山区高速公路平纵组合线形上的运行数据,建立了道路平纵组合线形设计对驾驶行为的影响仿真模型。梁士帅[21]通过建立运行速度预测模型与车路耦合安全模型,得出了不同车型在山区低等级公路不同线形的弯坡组合路段安全设计指标阈值,及其随设计参数变化的规律。李春生[22]基于运行速度设计方法通过对实际道路数据的采集及计算,对山区低等级公路线形安全性进行了改进。
以上对于山区公路弯坡路段的研究大多局限在对山区较高等级的高速公路弯坡组合路段,其中多是通过驾驶员生理反应或路段线形、汽车速度、载重或外界影响条件来对现有道路进行道路通行能力的安全性分析、仿真实验,相关领域的国内外学者对低等级公路弯坡组合路段的设计也少有研究,大部分研究集中在纵坡设计和平曲线设计方面[23]。文中考虑中小型汽车的非线性动力学特征,通过建立五自由度汽车动力学模型,对低等级山区弯坡组合路段道路安全性进行研究,并分析山区低等级公路的超高、坡度及圆曲线半径对汽车安全性的影响。研究结果可为山区公路设计提供更完整的非线性汽车动力学依据。
1 汽车动力学模型建立
由于主要考虑汽车的平面运动稳定性,所以文中研究不考虑车身俯仰和侧倾运动产生的垂直载荷变化对系统稳定性的影响,根据右手定则建立的六自由度汽车坐标系建立单轨汽车模型,汽车在车架坐标系内沿不同方向的受力情况如图1所示。
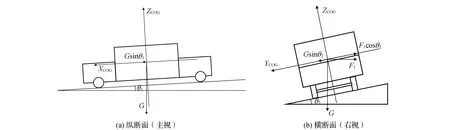

图1 弯坡组合路段汽车受力三视
以五自由度汽车动力学模型[24]为基础,考虑车速、道路坡度值和超高值对汽车动力学的影响,加入以地面附着力为最大制动力矩,建立汽车转向制动稳定性的非线性动力学分析模型为
(1)
滑移率方程为
(2)
轮胎侧偏角表达式为
(3)
魔术公式为
F=Dsin(Carctan(Bα-E(Bα-arctanBα)))
(4)
式中:m为整车质量,Iz为绕z轴的转动惯量,lf为汽车前轮到质心的距离,lr为汽车后轮到质心的距离,θ1为汽车坐标系纵方向汽车下坡坡面的坡度角,θ2为汽车坐标系侧方向平曲线超高的侧向坡度角,FI为惯性力,R为道路圆曲线半径,ih为道路超高值,iy为道路纵坡值,Cair_x为纵向空气阻力系数,Cair_y为侧向空气阻力系数,AL_x为纵向迎风面积,AL_y为侧向迎风面积,ρ为空气密度,Re为车轮转动半径,vx为汽车纵向速度,vy为汽车侧向速度,ω为汽车横摆角速度,ψ为车身横摆角。
2 汽车动力学模型验证
为验证模型准确性,本次采取的试验条件根据现有规范《公路工程技术标准》(JTG B01-2014)及《公路项目安全性评价规范》(TG/T B05-2015)设定为在三级、四级山区公路弯坡组合路段情况下,选取3种公路设计时速40 km·h-1、30 km·h-1、20 km·h-1作为最大车速设计实验进行验证。道路采用双车道模型,每条单车道路路幅宽度均为4 m,轨迹半径偏差值不超过道路路幅宽度限制,汽车稳定速度范围不超过规定速度,也不可小于最大车速减去1 km·h-1。汽车横摆角速度不超出非线性动力学求得的不稳定平衡点0.4 rad·s-1限定范围。坡度值设定为3%和9%,超高值设定为4%,找出3种标准情况下的最小极限半径。文中全程采用MATLAB软件进行仿真实验,如图2、图3所示。
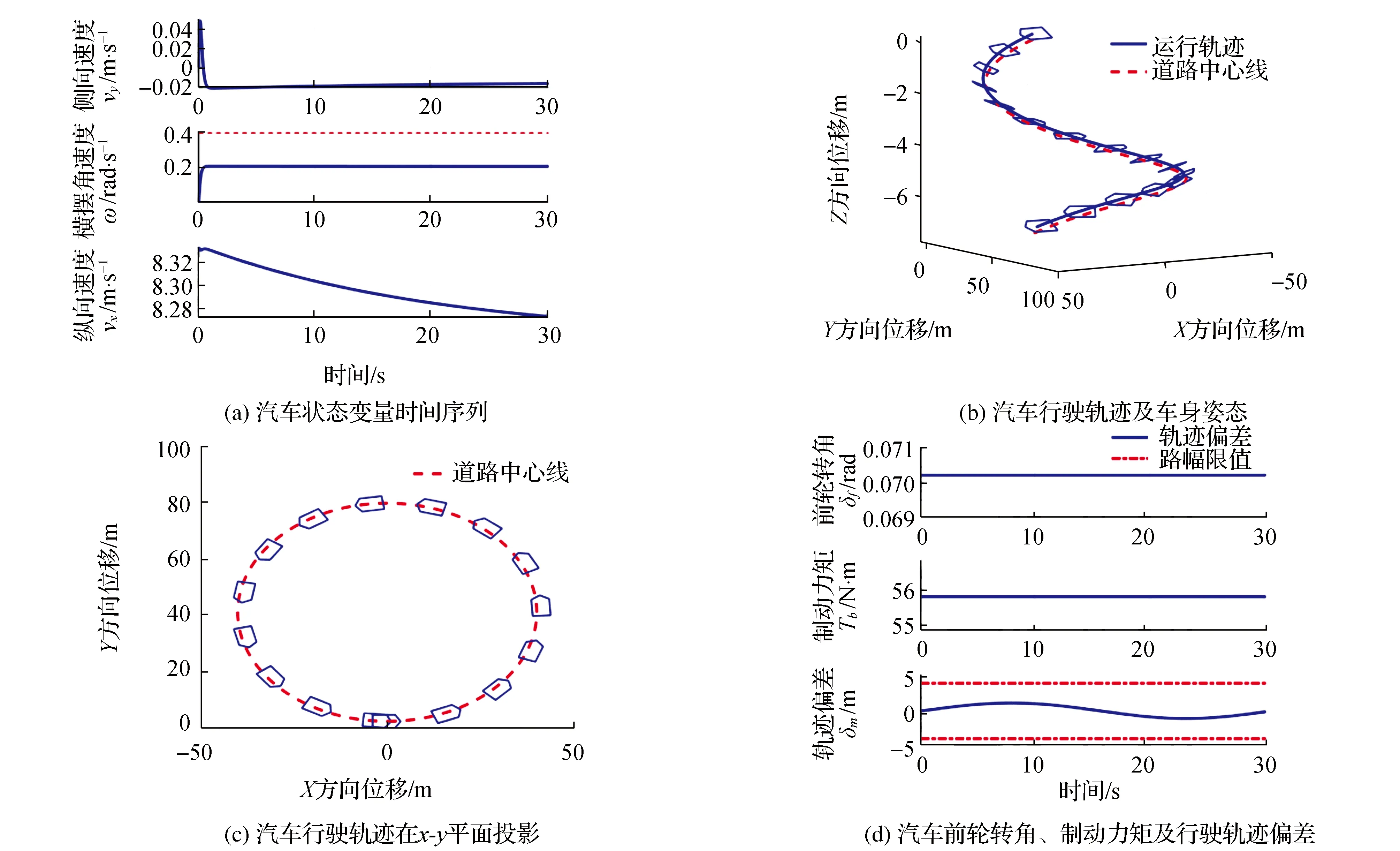
图2 纵向速度30 km·h-1,圆曲线半径40 m,纵坡3%,超高4%的仿真结果
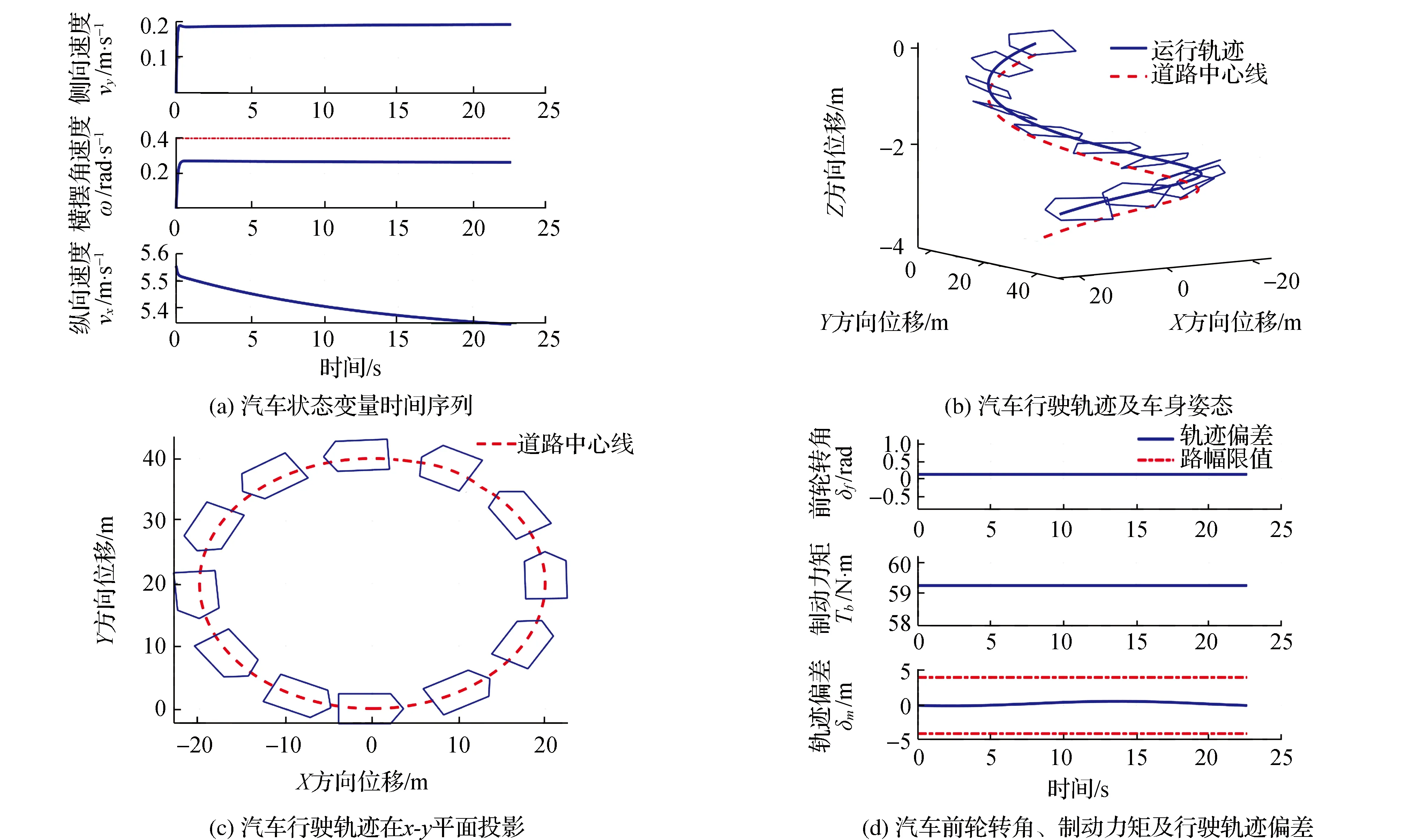
图3 纵向速度20 km·h-1,圆曲线半径20 m,纵坡3%,超高4%的仿真结果
由于篇幅限制,仅列出当纵坡值为3%、超高值为4%,速度为30 km·h-1、圆曲线半径为40 m以及速度为20 km·h-1、圆曲线半径为20 m时的仿真实验结果。从仿真结果可以看出,当汽车在这两种条件下行驶时,纵向、侧向速度及横摆角速度均可呈现稳定状态,横摆角速度不超出非线性动力学求得的不稳定平衡点0.4 rad·s-1限定范围,通过调节驱动及制动力矩,可使车速最后稳定在限定时速内。实验结果证明所建立的非线性分析模型能够体现汽车的运动学和动力学特征,可以分析山区低等级公路弯坡组合路段汽车转向制动稳定性。
3 弯坡组合路段安全性仿真
3.1 实验设计
本次实验将从低等级公路弯坡组合路段不同道路圆曲线半径角度入手,用非线性汽车动力学结果来分析山区低等级公路在已存在坡度和超高的情况下,不同纵坡超高组合下保证公路安全性的圆曲线半径极限值。实验条件及目的如表1所示。

表1 实验设计条件
3.2 实验结果
由图4中第1组实验结果可知,当纵坡为3%,超高值为4%,圆曲线的半径为34 m,最大时速为40 km·h-1时,汽车在山区低等级公路弯坡组合路段行驶,此时可以看出汽车的纵向、侧向速度及横摆角速度呈现稳定状态,横摆角速度在0.3 rad·s-1左右,不超出非线性动力学求得的不稳定平衡点0.4 rad·s-1限定范围,由于能量存在耗散,车速略有减小,通过调节驱动及制动力矩,可使车速最后稳定在39~40 km·h-1之间。汽车质心轨迹半径偏差在道路等级限制路幅宽度内。当纵坡、超高及时速不变,圆曲线半径缩小至33 m时,汽车的纵向、侧向以及横摆角速度出现突变,为存在较大波动的不稳定状态,汽车质心轨迹半径偏差超出道路等级限制路幅宽度。由此可判断汽车在纵坡为3%,超高为4%,最大时速为40 km·h-1时,根据非线性汽车动力学,道路圆曲线半径最小值为34 m。
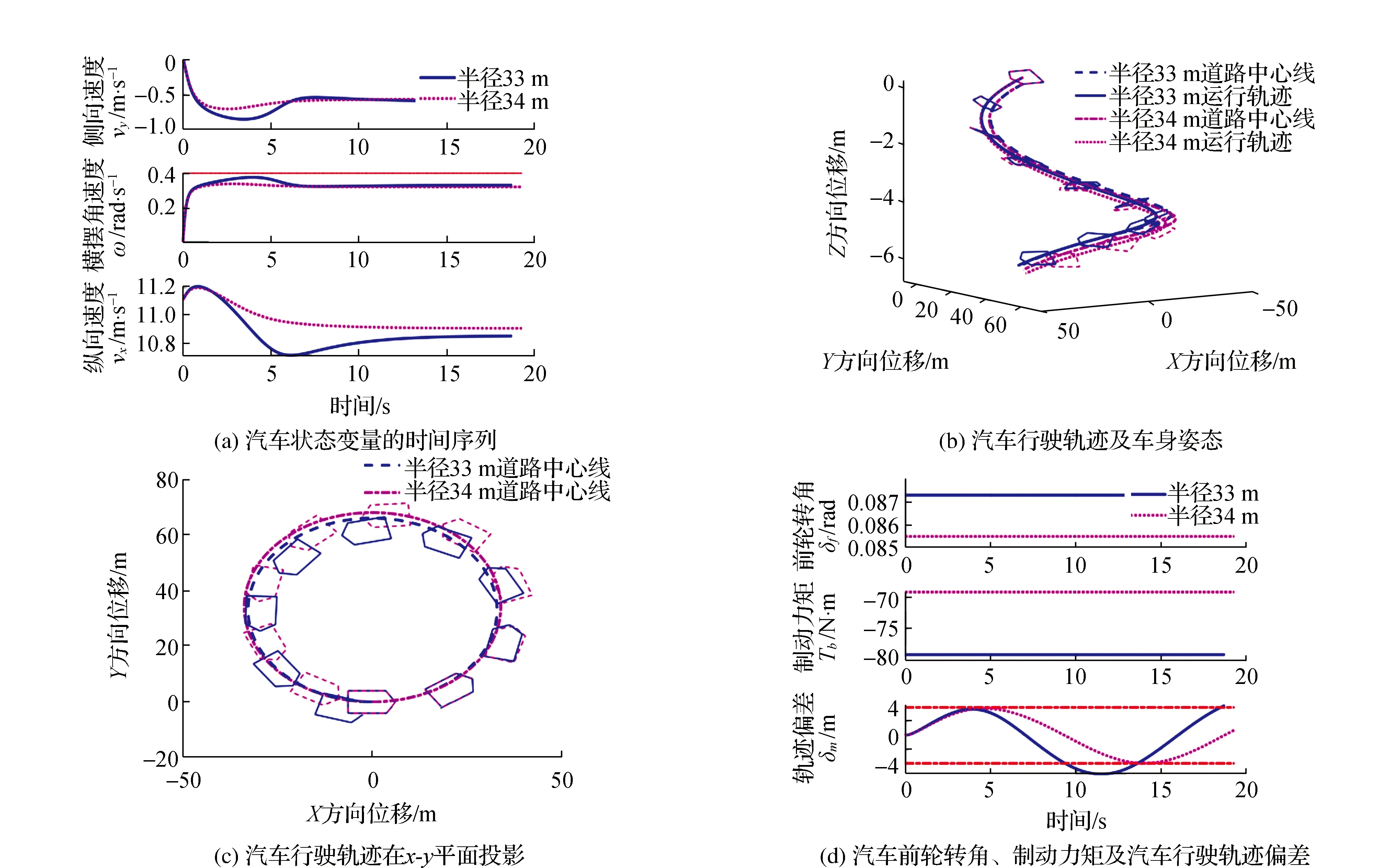
图4 纵向速度40 km·h-1,圆曲线半径33 m,34 m,纵坡3%,超高4%的仿真结果(实验1)
由图5中第2组实验结果可知,当上组实验稳定结果34m结果中其他限制条件不变,纵坡变为4%时,汽车的纵向、侧向以及横摆角速度未存在较大波动,仍为稳定状态,但汽车运动质心轨迹半径偏差超出等级限制路幅宽度。由此可判断汽车在纵坡值为4%,超高值为4%,最大时速为40 km·h-1时,根据非线性汽车动力学,道路圆曲线半径最小值不能取34 m,应至少增大至35 m。可得出结论为,随着纵坡坡度增加,圆曲线半径的可取最小值也会相应增加。

图5 纵向速度40 km·h-1,圆曲线半径34 m,纵坡3%,4%,超高4%的仿真结果(实验2)
由图6中第3组实验结果可知,当纵坡为3%,超高值为4%,圆曲线的半径为33 m,最大时速为40 km·h-1时,此时可以看出汽车的纵向、侧向以及横摆角速度出现突变,为存在较大波动的不稳定状态,汽车质心轨迹半径偏差超出等级限制路幅宽度。当超高值由4%增至6%时,汽车的纵向、侧向速度及横摆角速度变得更稳定,横摆角速度在0.3~0.35 rad·s-1左右,不超出非线性动力学求得的不稳定平衡点0.4 rad·s-1限定范围,由于能量存在耗散,车速略有减小,通过调节驱动及制动力矩,可以使最后稳定车速在39~40 km·h-1之间,汽车质心轨迹半径偏差在等级限制路幅宽度内。可得出结论:在弯坡组合路段,随着超高的增加,圆曲线半径可取的最小极限值也将相应减小。

图6 纵向速度40 km·h-1,圆曲线半径34 m,纵坡3%,超高4%,6%的仿真结果(实验3)
综上:当汽车速度相同,随着半径的减小,汽车的动力学状态将发生突变,运行轨迹将超过路幅宽度;在不发生失稳的情况下,随着纵坡坡度值的增大,弯坡组合路段可取的最小极限值圆曲线半径也随之增大;而随着超高值的增大,弯坡组合路段可取的最小极限值圆曲线半径随之减小。
3.3 弯坡组合路段安全性分析
根据不同等级公路的设计车速和公路弯坡组合路段坡度超高限制,可通过此方法得到汽车在高附着路面下不同等级公路车速上安全运行的最小极限转弯半径,如表2所示。
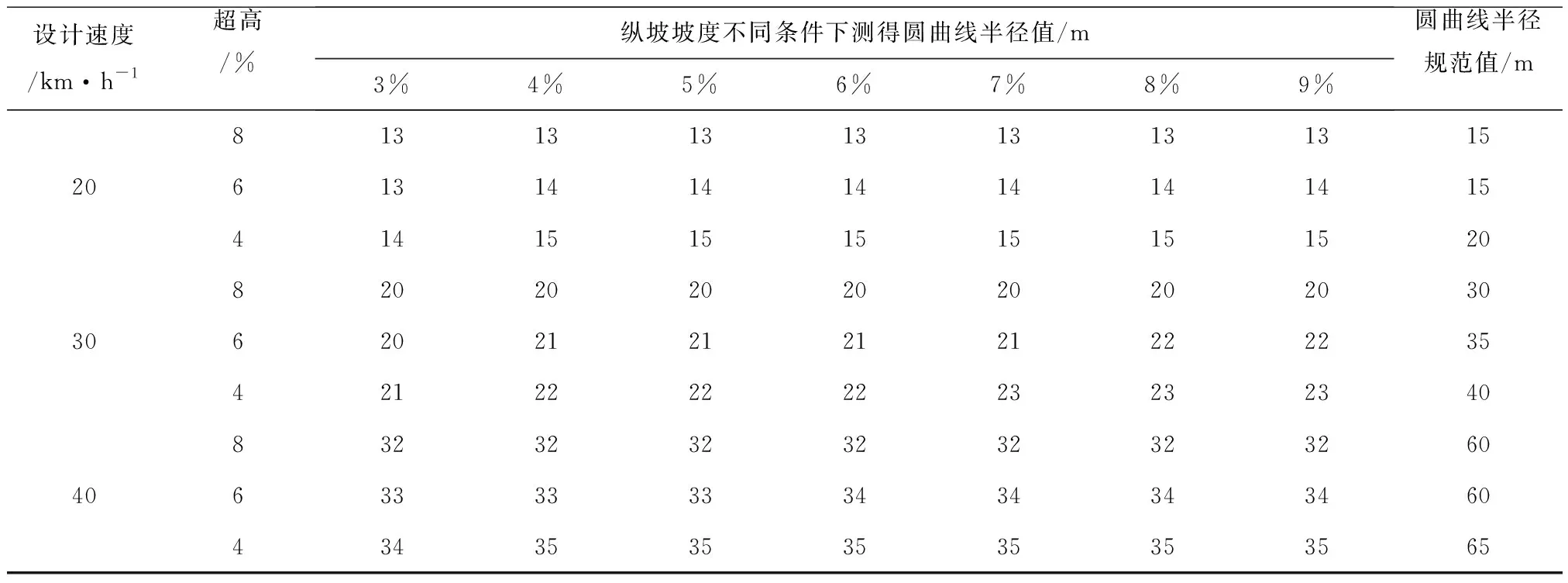
表2 实验结果
在相同速度条件下,当超高值为4%和6%时,随着纵坡坡度的增加,圆曲线半径最小值也会相应增加,但增加趋势不明显。当超高增大为极限值8%时,纵坡变化对应圆曲线半径极限值不变。但此时制动力矩会出现急剧增大,前轮转角变化范围减小。
在相同速度条件下,当纵坡坡度值相同,超高值由4%增加到8%,不同速度对应的公路圆曲线半径最小极限值相应减小。
在超高值和纵坡值相同的条件下,随着速度的增加,不同速度对应的公路圆曲线半径最小极限值相应增大。
4 结 论
针对山区低等级公路弯坡组合路段汽车转向制动工况,建立了汽车转向制动稳定性的非线性分析模型,以不同等级公路车速、超高及纵坡坡度为条件进行仿真分析,从非线性汽车动力学角度对弯坡组合路段的安全性规律进行分析,得到以下结论。
1)随着车速的减小、公路超高值增大或纵坡值减小,汽车稳定安全行驶最小半径极限值均会随之减小。
2)当超高值达到8%时,纵坡值无论变大或变小,圆曲线半径极限值均保持不变。
3)通过非线值提供非线性动力学判断依据。
在未来的工作中,将研究低附着路面以及实际道路的应用情况,通过混合算法得到非线性系统的平衡点求解。
