地铁换乘站客流滞留模型

何 君，雷爱国，吴翊恺，李陈洋

(南京理工大学 自动化学院，南京 210094)

随着城市轨道交通的高速发展，多条地铁线路穿梭在城市的各个区域，通过换乘站的衔接编织成一张通达各地的地下交通网络[1]。地铁换乘站使得乘客在不同路线之间，在不离开车站付费区及不另行购买车票的情况下便可进行跨线乘车，是交通网络的关节所在，也是地铁线路客流最为集中之地[2-4]。由于工作日早高峰换乘乘客和进站乘客的大量汇入，列车往往无法将候车乘客及时疏散而导致换乘站台的乘客滞留[5]。同时，到站下车的乘客将对站台形成脉冲式的客流冲击，会导致站台更加拥挤，影响车站的安全运营[6-7]，如何缓解乘客滞留现象成为一个亟待解决的问题。

为提高换乘站的运营效率，国内外的专家学者已经组织开展了较多的理论研究。王婵婵等[8]以上海地铁江苏路站为例验算了不同行车密度下的换乘站客流疏解与滞留情况；结合列车运行条件的影响，傅晨琳[9]等提出了不同滞留程度下的地铁侧式站台的人数计算模型；SERIANIS[10]等通过实际规模的实验探究了列车行车间隔、上下车人数等因素对站台人群密度的影响，但缺乏对乘客滞留现象的分析。在缓解乘客滞留方面，李艺[11]等从客流分配的方向构建了最优换乘路径模型；赵保锋[12]等提出了获取客流滞留分级预警关键控制点的方法；ANSARIE研究[13]表明，缩短发车间隔时间可以有效减少乘客的候车时间和滞留人数。为提高换乘站的换乘效率，杨楠[14]通过AnyLogic仿真找出了人流的瓶颈，并验证了优化措施的可行性；Svistunova[15]利用AnyLogic软件建立离散事件模型，实现客运交通建模程序，用于寻找车站客流组织和旅客服务的最优解。

综上所述，目前对于大客流条件下乘客滞留现象的定量分析尚存在一定的局限性。因此，文中在分析地铁换乘站早高峰客流特征和发车间隔对滞留现象影响的基础上提出一种考虑站台设施布局的滞留人数计算模型。同时，在实际数据集的基础上在Anylogic中搭建仿真环境，并对模型进行验证。实验结果表明，模型在滞留人数预测方面表现优异，可以有效地反映客流的滞留情况，研究成果可为缓解换乘站的滞留现象提供思路与灵感。

1 工作日早高峰客流滞留模型

由于地区间的交通出行量不平衡，城市轨道交通全日客流量会形成两个高峰时期[16]。调查发现，工作日的早高峰是换乘站乘客滞留情况最为严重的时期且持续时间相对较长，滞留现象的严重程度主要取决于地铁线路的行车计划与客流分布之间的供需关系。

1.1 早高峰客流特征

南京城市轨道交通的早高峰定义为07:00—09:00，但在地铁客流方面的研究中通常以1 h作为研究对象，将一天24 h中客流量最高的某段时间记为高峰时段，在此期间存在10～15 min的时间客流达到峰值，即超高峰时期。与节假日不同之处在于，工作日早高峰的客流量更加稳定，不易受重大活动等突发因素的影响。工作日早高峰时段多为工作上班人员和学生，时间限制没有晚高峰时期那么宽裕，对上车的期望相对较高，因此造成地铁车厢内部异常拥挤。在乘客大规模涌入的同时，车门乘降区的立席密度过大，这将导致部分乘客滞留在站台，同时到达站点下车的乘客将会对站台形成脉冲式的客流冲击，将会进一步导致站台乘客密度骤增，因而对车站的疏散能力提出了更高的要求。在客流特征分析之前，做出以下两项假设：

假设1：每位乘客视为相互独立的个体，滞留决断互不影响；

假设2：每位乘客不作长时间逗留，最多滞留3次。

1.1.1 候车客流特征

工作日早高峰换乘站的客流主要由进站客流Q1(人·h-1)和换乘客流Q2(人·h-1)组成，则早高峰乘车总客流为Q=Q1+Q2。由于早高峰客流具有时变性和不确定性等特点[17]，选取整点1 h作为研究对象存在一定的误差，文中选取早高峰连续客流最大的60 min作为高峰小时。然而客流在高峰小时内仍具有波动性，通常采用超高峰系数Pmax来作为衡量超高峰时段客流的标准。《地铁设计规范》(GB 50157—2013)规定超高峰系数取值一般为1.1～1.4，且在换乘站中取值相对较高。Pmax计算方法为

(1)

式中：Qmax为超高峰时期客流，人·h-1;Q为高峰小时客流，人·h-1。

如图1所示，设高峰小时内客流到达规律满足分段一次函数关系式

图1 高峰小时内客流到达规律示意图

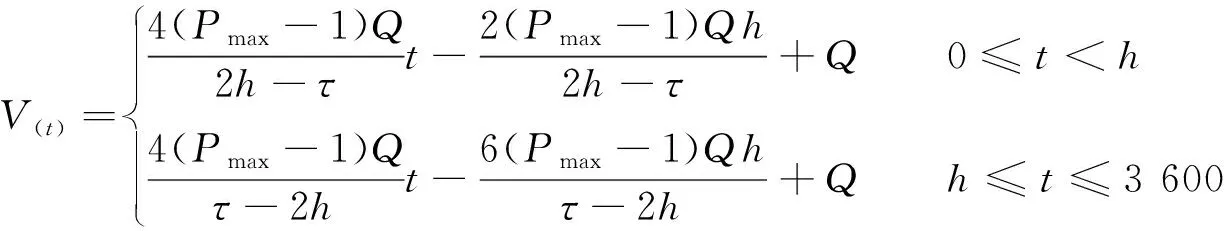
(2)

式中：V(t)为t时刻客流到达的速度，人·h-1；τ为超高峰时期持续时间，取值为10～15 min；h为超高峰时刻，即客流最大时刻，s。

若早高峰开始时站台的初始滞留人数为K0、高峰时期列车开行对数为Z(pcu·h-1)、发车间隔时间为T(s)，则可将高峰小时划分为Z个时间长度为T的候车周期,第i个周期内(i=1,2,3,…,Z)候车乘客的数量随时间t的变化满足

(3)

式中：S(t,i)为第i周期内t时刻站台的候车人数，人；L(i-1)为上一周期末滞留的乘客数量，人；L(i)为第i周期末滞留的乘客数量，人。

第i个周期内，候车人数随着乘客的涌入而不断增加，列车到达站台时刻候车人数达到该周期内的峰值。乘客上车后列车开始启动，由于客流量较大将出现乘客滞留现象，滞留乘客的数量便成为下一候车周期的初始候车人数，于是站台候车人数在每次车辆到达时会表现出脉冲式的下降趋势，并在下一候车周期逐渐恢复，其变化趋势具有一定的周期性。由此可统计出高峰小时内最大候车人数为

Smax=maxS(t,i)

(4)

进而可以得到站台最大人群密度以及疏散压力。

1.1.2 乘客滞留特征

客流量较大会提高候车乘客滞留的可能性，由于乘客在各个车门前的排队长度有所差异，因此各车门前滞留情况的严重程度也不尽相同。城市地铁线路中的列车通常采用固定编组，线路上各站点的站台车门数量相同。设换乘站台的车门数量为M，则列车到达时单车门前滞留乘客的数量L(m,i)(m=1,2,3,…,M)受该车门前的候车人数S(m,t)和车门乘降区立席密度ρ(m)的影响，立席密度是指城市轨道交通车厢有效站立面积内，单位面积平均站立的乘客人数。候车人数和车门乘降区立席密度过大会导致滞留人数增加。

各车门候车区的候车乘客数量受车门的位置以及与扶梯口的距离等因素影响而各有所异。研究发现，站台中部以及靠近扶梯口的车门前更容易吸引乘客聚集，因此滞留现象也更为严重。为研究乘客在各车门前的分布情况，构建车门吸引子模型，如式(5)所示，设站台的扶梯口数目为J，则t时刻车门m对j号扶梯口处乘客的吸引力为

(5)

式中：F(m,j,t)为t时刻车门m对j号扶梯口处乘客的吸引力向量；k为引力系数，取值依站台设施布局而定；Cm为车门m前候车区域的乘客容量，人；R(m,j)为车门m和j号扶梯口间的距离，m；S(m,t)为t时刻车门m前候车乘客的数量，人。

则t时刻车门m对乘客的吸引子为

(6)

当t时刻某乘客经由扶梯j到达站台后，将前往最具有吸引力既吸引子最大的车门前进行候车。结合客流到达站台的速度可得t时刻车门m前的候车人数为

(7)

式中：L(m,i-1)为上一候车周期的滞留人数，人。

单车门前的滞留人数与候车人数[18]符合线性关系式(8),单车门前的滞留人数与车门乘降区立席密度满足二次多项式(9)。

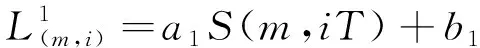
(8)

(9)

式中：a，b，c均为常数；ρ(m,t)为t时刻m车门乘降区的立席密度，人·m-2。

由此可得第i个周期结束时列车开走后站台的总滞留人数为

(10)

站台两端处的车门由于与各扶梯口的距离相对较远、乘降区立席密度不高、候车区域的乘客较少等因素，通常只产生轻微的滞留。研究表明，进入早高峰伊始站台的各车门前便出现不同程度的乘客滞留现象，并随着时间的推移愈发严重，在超高峰时期站内的候车人数和滞留人数均达到顶峰，直至早高峰结束滞留现象才得以缓解。

1.2 发车间隔对滞留情况的影响

发车间隔是指前后两班次列车驶离始发站的时距，是编制行车时刻表的重要指标[19]。工作日早高峰的换乘站具有候车人数多、乘客滞留现象严重、站台人群密度高等特征。若高峰小时内发车间隔过大，线路中的滞留客流将迅速上升，列车内的立席密度也会随之增加，乘客难以上车的同时站台的候车人数继续堆积，导致站台的乘客难以疏散。而减小发车间隔势必造成轨道交通运营成本的增加和一定的资源浪费。因此，合理地调整发车间隔是制定列车开行计划的前提。

由于列车在运行过程中受行驶速度、乘降时间等不确定因素影响，高峰小时内到达换乘站的列车数量N(pcu·h-1)并非固定值。如图2所示，N的取值有两种可能。若第1趟及第Z+1趟列车均能在高峰小时内到达站台，则N的取值为Z+1，否则取值为Z。

图2 到站列车数与间隔时间的关系

N的取值概率服从Bernoulli分布，其概率质量函数为

(11)

由式(7)、式(11)可知，当发车间隔为T时，高峰小时平均滞留人数和最大候车人数分别为

(12)

maxS(Z+1)

(13)

减小早高峰发车时间间隔可以疏解换乘压力，降低候车区的人群密度和滞留人数；发车间隔时间过大时，轨道交通线路的服务水平很难满足运营管理的需求。

2 参数配置

选取南京地铁大行宫站为例对模型进行仿真分析。南京地铁3号线工作日单日客流量在65万人次以上，2号线则高达70万人次以上，大行宫站位于南京市秦淮区中山东路与太平北路、太平南路交叉路口北侧，是地铁2号线和3号线的换乘车站，也是南京地铁交通网络中客流最为集中的站点之一。选取3号线往2号线油坊桥方向换乘作为研究主线并在AnyLogic软件中进行仿真。

2.1 大行宫站设施布局

在对滞留模型进行仿真之前，需搭建乘客的交通环境[20]。大行宫站地下部分共3层，站厅位于地下一层，2号线站台为东西向地下二层岛式站台，3号线站台为南北向地下三层岛式站台。通过对大行宫站实地调查，整理得到大行宫站站台基本情况如表1所示。

表1 大行宫站站台基本情况

在站层图的基础上，结合实地考察数据，在AnyLogic软件中绘制的大行宫站设施布局三维模型如图3所示，其中模型比例为1 m=7像素。

图3 大行宫站设施布局三维模型

2.2 客流流线及行为流程

根据规划和现场调研的大行宫站运营组织管理信息，结合该站的站层图，按方向、目的地等属性依次获取客流流线，同时标记出乘客在客流流线中可能访问的设施、禁行区域[21]等。如图4所示，客流流线主要包括进站客流流线以及换乘客流流线。

图4 客流组织形式

进站客流从各出入口进入大行宫站后选择使用交通卡或购买单程票后由进站闸机进入站厅，并乘坐下行扶梯到达2号线站台候车。换乘客流从3号线站台搭乘上行扶梯至站厅后乘坐下行扶梯至2号线站台候车，也可直接通过便捷换乘通道到达2号线站台。

在获取客流流线后，对乘客的行为流程进行建模。乘客的行为是指乘客在出行过程中，受交通环境、生理和心理因素影响而表现出来的一系列与交通相关的交通活动。AnyLogic行为建模的基础理论是离散事件建模(以过程为中心的建模方法)[22]，将乘客在交通环境中的活动划分为不同的行为过程，并连接成乘客的行为链[23-24]，绘制乘客行为流程图如图5所示。

图5 AnyLogic乘客行为流程图

乘客来源为大行宫站各出入口以及三号线站台，在智能体面板中创建参数Speed、事件Event等组件,并按式(2)编写相应程序控制乘客到达速度。乘客行为主要包括：步行、购票、安检、检票、搭乘扶梯、候车等。

2.3 交通特性数据

为了准确模拟站台的滞留情况，必须确定车站的交通特性数据，主要包括客流量、乘客到达时间分布规律、乘客步行速度、安检及购票等待时间、乘客在各车门前的分布规律等，通过实地调查获取以上数据。选取2021年4月连续10个工作日的大行宫站交通卡数据进行分析，得平均早高峰进站客流变化规律如图6所示。

图6 大行宫站工作日早高峰进站客流时间分布

以15 min作为分析单元，超高峰时期为07:45—08:00时间段，高峰时段均出现在07:30—08:30。本次调查采用人工计数法和视频录像法[25]，每日固定调查大行宫站高峰时段的滞留情况，记第一趟列车所滞留的乘客数量为初始滞留人数；客流的平均观测数据如表2所示。

表2 大行宫2号线车站油坊桥方向平均客流统计

由表2可知，工作日早高峰时期客流规模庞大，且大部分是换乘客流，发车间隔难以满足客流需求，站台的初始滞留比例为10.04%。调查发现每日的08:00左右客流达到峰值，超高峰系数为1.3，购买单程票的比例为9.85%。按年龄、性别等属性依次统计乘客的正常步行速度情况如表3所示，乘客上、下楼梯的速度分别为正常步速的0.5、0.9倍，乘客在自动扶梯上时保持站立。

表3 乘客步行速度统计 m·s-1

大行宫站环境设施及行人模块仿真参数如表4所示。

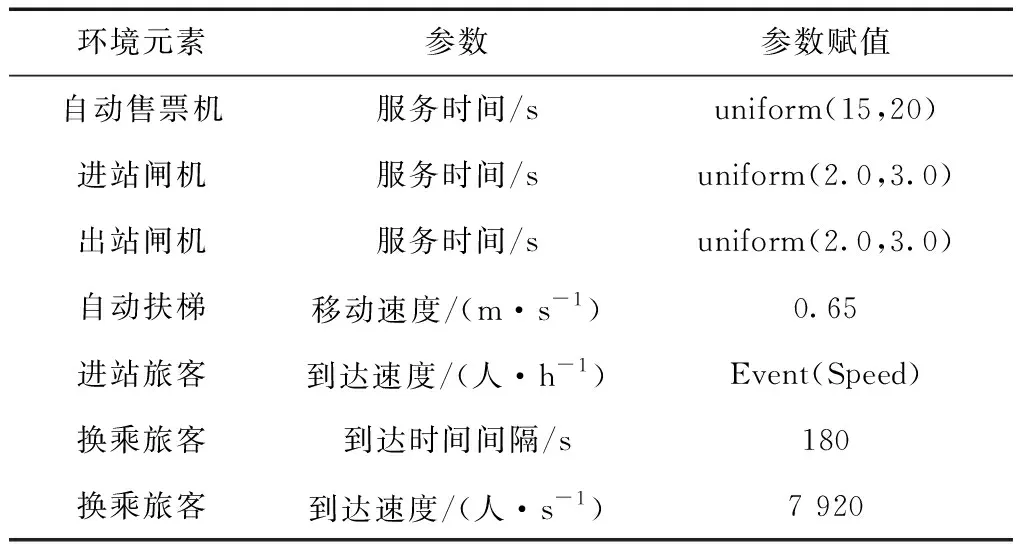
表4 Anylogic仿真参数

2号线采用6节A型列车编组，每节车厢5个车门，共计30个车门，自西向东从1至30依次编号，统计各车门前平均候车人数、乘降区平均立席密度、平均滞留人数情况如图7所示。

由图7可知，各车门前的乘客数量分布并不均衡，单个候车区容量为25人左右，其中站台中部的车门前排队的候车人数相对较高，各车门前均存在不同程度的滞留现象，而立席密度差别并不明显。

图7 大行宫2号线车站各车门客流情况统计

3 结果分析

为探究单车门前滞留人数与候车人数、立席密度的关系，将观测数据在Matlab中进行拟合。

1)将站台的滞留人数与候车人数进行相关性分析，二者符合线性关系式(8)，拟合结果及曲线如图8(a)所示；

2)将站台的滞留人数与乘降区立席密度进行相关性分析，结果符合二次多项式(9)，拟合结果及曲线如图8(b)所示。

图8 大行宫站工作日早高峰观测数据拟合结果

表5 拟合结果

由拟合结果可知，置信区间为95%时拟合优度均在0.9以上。结合以上数据，在Matlab中循环仿真10次并取结果的平均值，得2号线站台平均滞留情况与实际观测数据对比情况如图9所示。

图9 乘客滞留人数计算值与观测值对比

在AnyLogic中进行仿真实验，仿真时长60 min，统计高峰小时内站台候车乘客数量变化情况如图10所示。

由图10知，在实际过程中乘客的到来以及是否滞留均具有随机性的前提条件下，模型能够有效地模拟出乘客的滞留情况。大行宫站早高峰2号线站台出现大量乘客滞留，08:00左右滞留情况最为严重，滞留人数由初始的52人迅速上升至160人左右，滞留比例上涨6.44%，站台候车人数增长十分明显。由于08:00之后乘客到站的速度开始下降，滞留情况得以逐渐缓解，但速度缓慢，直至高峰小时结束也无法完全消除滞留；高峰小时结束时，站台滞留人数仍维持在110人左右，滞留比例约为3.28%，站内候车乘客数量高达600余人。

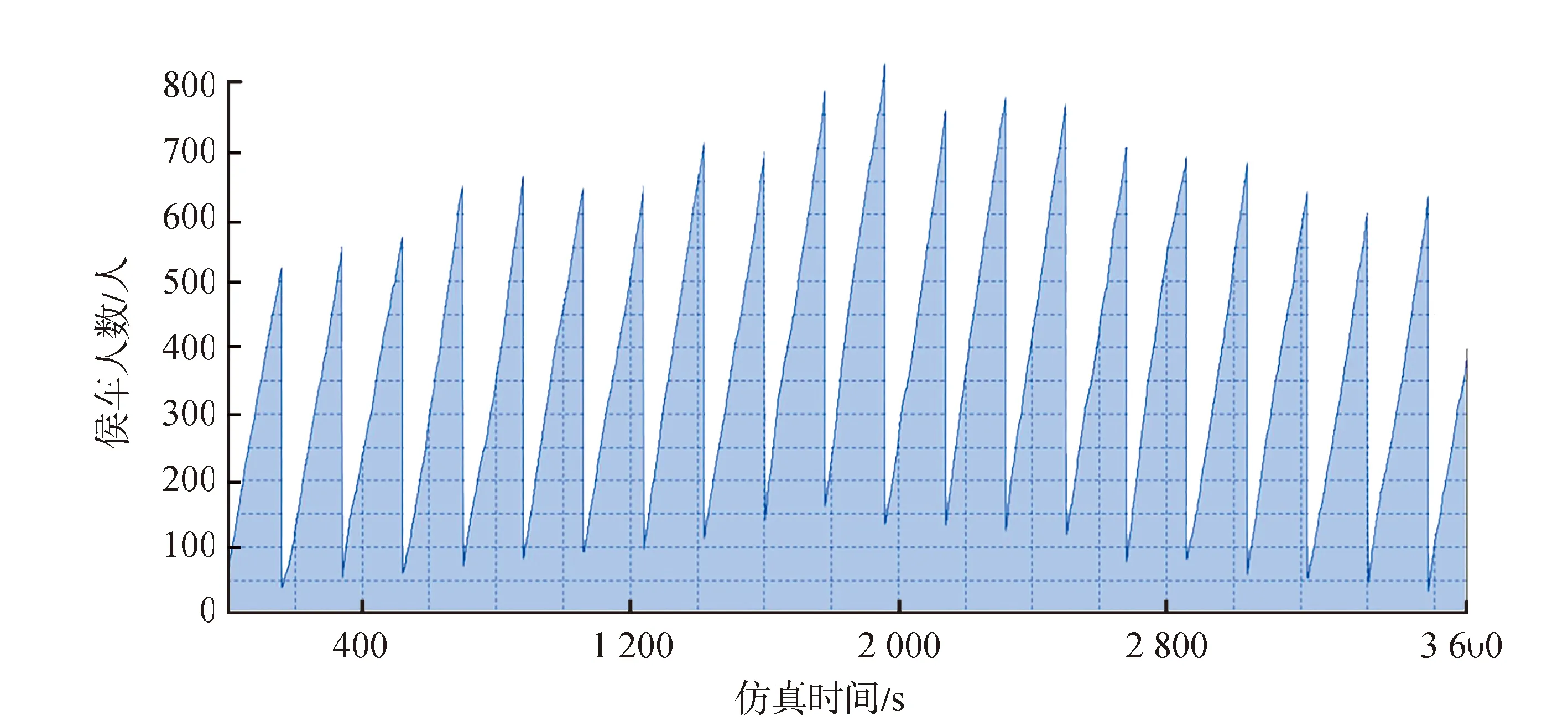
图10 07:30—08:30站台候车人数变化

AnyLogic仿真表明2号线站台滞留乘客主要集中在图11中的A、B、C、D、E 5处区域，占全站台滞留人数的64.8%，各区域的位置及滞留影响因素如表6所示。

表6 滞留区域位置及原因

图11 超高峰时刻站台滞留人群密度(单位：人·m-2)

结合各区域的滞留原因，提出如下优化措施：

1)对于客流量过大，在采取限制进站客流措施的同时，综合2号线运行情况适当减少发车间隔,增加运行车辆；

2)对于各滞留严重区域，建议安排站务人员引导乘客前往候车人数低的车门前候车，将客流均匀分布在各车门前；

3)对于各扶梯口及换乘通道出口，建议安排站务人员指挥乘客快速通行，尽量避免乘客拥堵在出口处。

AngyLogic仿真发现，当模拟加入站务人员指导、限制进站客流至4 000人·h-1、调整2号线发车间隔为160 s时，站台的滞留情况得到了初步缓解。如图12所示，优化后虽仍存在若干个滞留相对严重的区域，但滞留人数和站台整体的人群密度都明显降低；优化前后滞留人数随列车到达次数的变化情况对比如图13所示；取5次仿真数据并求取各区域的平均值与优化前对比情况如表7所示。

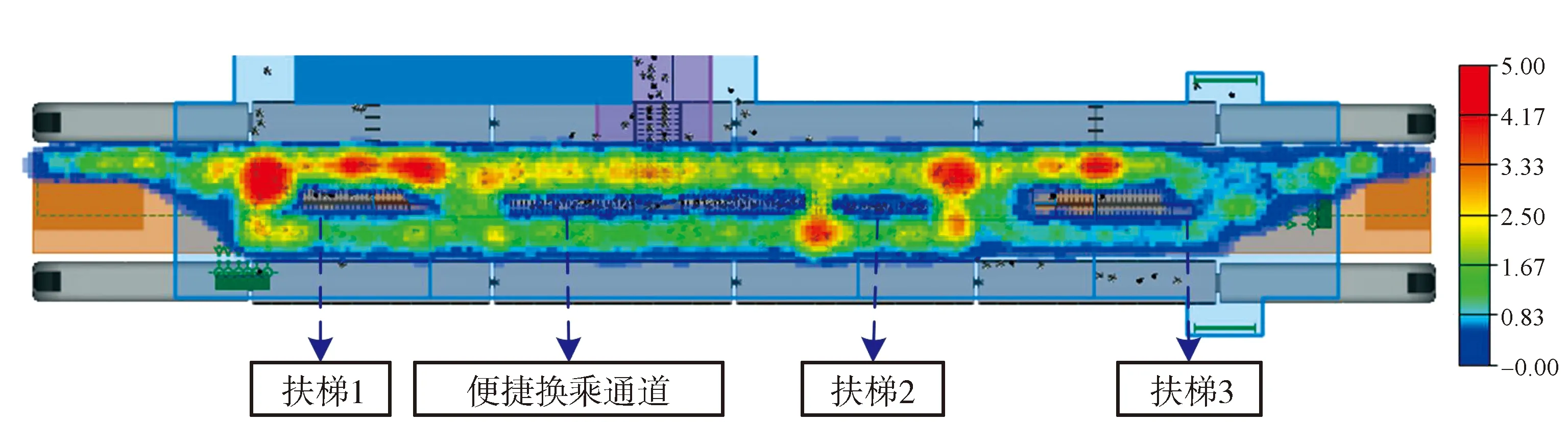
图12 超高峰时期滞留人群密度

图13 优化前后站台滞留人数对比

表7 重点区域平均滞留情况对比

优化后A、B、C、D 4个区域的滞留情况得到了有效缓解，其中B、C区域的优化效果最佳，主要原因是换乘客流被引导分散至其余区域候车，降低了B、C区域的候车人数，疏散压力明显减轻。然而分摊客流必然导致部分车门前的滞留现象加重，如E区域优化后平均滞留人数增加了0.12人，但站台整体滞留人数还是有较大幅度的降低。缩短发车间隔使得线路的运力大幅度提升,乘客得到了有效的疏散，高峰小时内到达站台的车次由20趟增加至22或23趟，高峰小时结束时站台的滞留人数相比于优化前下降50%，缩短滞留现象的持续时长。

4 结 语

文中主要研究了地铁换乘站早高峰客流滞留问题，基于大行宫站交通卡及现场调研数据提取了候车客流的到达及滞留特征，在此基础上构建地铁换乘站客流滞留模型，并提出候车区吸引子的概念，将站台设施布局对乘客分流的影响进行量化。通过Anylogic搭建大行宫站三维环境及行人流线开展仿真实验：一方面，验证所提出滞留模型的合理性；另一方面，分析站台滞留乘客的分布特征及滞留的原因并提出改善措施。研究结果表明：1)模型在各个候车周期结束时都能计算出可靠的滞留人数，能够真实地反映客流的滞留情况；2)站台内滞留乘客的分布并不均匀，靠近扶梯口的候车区滞留现象较为突出；3)采取减小发车间隔、适当限流、派遣站务人员分散候车客流的方式能够在一定程度上降低滞留的比例。

文中目前解决了换乘站早高峰的滞留分析问题，但发车间隔对滞留程度影响的定量分析问题还需要进一步的研究。另外，基于站台密度及滞留比例的滞留程度评价方法是后续的研究对象。