带有恶化效应的松弛工期窗口排序问题
2022-03-16骆思雯王吉波
黄 雪,骆思雯,王吉波
(沈阳航空航天大学 理学院,沈阳 110136)
传统的排序问题通常假设任务的加工时间是常数。但在现实中,很多任务的加工时间往往随着开始时间的变化而变化[1]。如果任务的开始时间晚,那么它的加工时间就可能变长,这就是常说的恶化效应。比如火灾救援中,消防人员到达火灾现场的时间越晚,抢救火灾的时间就会越长。钢铁生产中,如果钢件处理有延误就会导致加工时间变长。目前已经有很多文献研究带有恶化效应的排序问题,如Gupta等[2]、Huang等[3],Wang 等[4],Li等[5],Sun等[6]。
近年来,准时制(JIT)已经广泛应用于现代制造业和供应链中。而在准时制策略中,企业向客户交付产品或服务时,通常企业被允许有一个时间间隔,这个时间间隔被称为工期窗口。一般用窗口的位置和长度来确定工期窗口。工期窗口过大,顾客不能接受,可能会导致顾客的流失;工期窗口过小,缺少生产弹性,企业不能接受。所以为了权衡双方的利益,非常有必要确定每个任务合理的工期窗口。在工期窗口前完工的工件要受到提前惩罚,在工期窗口后完工的工件也要受到延误惩罚,这就是工期窗口分配问题[7]。工期窗口一般可分为共同工期窗口、松弛工期窗口和不同工期窗口。Kramer等[8]研究了共同工期窗口排序问题。Liu等[9]研究了具有简单恶化的共同工期窗口问题;Huang等[10]研究了具有一般恶化效应的共同工期窗口问题;Wang等[11]研究了既有学习效应又有恶化效应的松弛工期窗口和不同工期窗口问题;Yue等[12]研究了简单线性恶化的松弛工期窗口和不同工期窗口问题;Wang等[13]研究了与位置有关的加权窗口问题;Zhang等[14]研究了简单线性恶化下两个目标函数的共同工期窗口和松弛工期的窗口问题。
本文将工件加工时间具有一般线性恶化效应的共同工期窗口指派问题[10]推广到松弛工期窗口上。目标是确定工件的排列顺序、窗口的开始时间和结束时间,使得两种目标函数达到最优。一个目标函数为提前时间、延误时间、窗口开始时间和窗口长度的加权和;另一个目标函数为提前任务数、误工任务数、窗口开始时间以及窗口长度的加权和。同时对所提出的问题给出多项式时间算法。
1 问题的描述

(1)
(2)
其中系数α≥0,β≥0,γ≥0,δ≥0,利用三元组记号法,以上两个问题可以表示成
其中SLKDW(Slack Due Date Window)表示松弛工期窗口。
研究分两部分解决上述两个目标函数问题。
2.1 基本结论
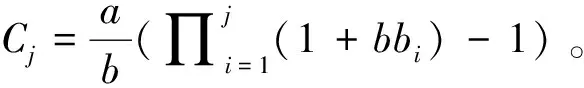
易知,此问题一定存在着一个所有工件被连续加工而没有空闲时间的最优顺序。
由文献[16]可知,下面两个引理成立。
引理2 对于任何指定的工件顺序φ,一定存在最优的q1,q2值,即q1=C[l*-1],q2=C[k*-1],其中l*=min{max{0,|(n(δ-γ))/α|},n},k*=min{max{0,「(n(β-δ))/β⎤},n},[l]代表工件被排在第l个位置,这里C[0]=0(此处,由q1≤q2可知l*≤k*)。

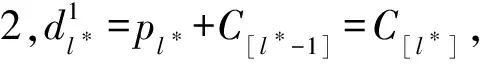
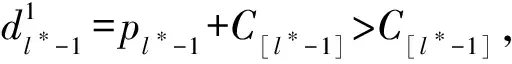
由引理1可知,{J[1],…J[l*-1]}∈E,J[k*]∈O,{J[k*+1],…J[n]}∈T,{J[l*+1],…J[k*-1]}∈W。若l*=0,则无提前工件;如果l*=k*,则窗口里无工件;如果k*=n,则无延误工件。

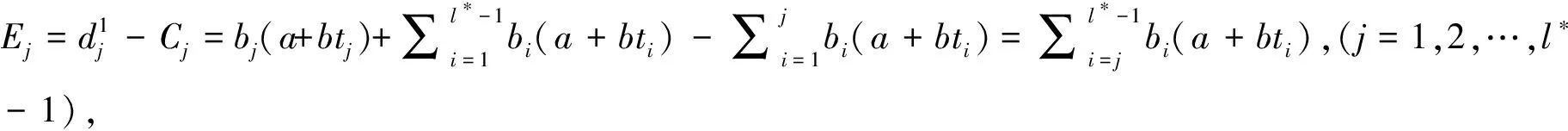

而Tj=0,(j=1,2,…,k*-1),那么有


由此可整理出
2.2 最优的工件加工顺序
引理3 最优顺序中必满足:
(1)各个集合内部顺序为:
①集合E里的工件按照LDR顺序排列;
②集合O∪T中工件按SDR排列;
③集合F∪W中工件按任意顺序排列。
(2)集合之间的顺序为:
①集合F∪W中工件的恶化率要小于集合E和集合O∪T中工件的恶化率;
②集合E和集合O∪T中工件需要进一步按照引理4进行判断。
证明:运用反证法和相邻交换法易证,具体可参见文献[12]。
引理4 假定工件Ju和Jv分别排在x和y的位置(1≤x≤l*-1,k*+1≤y≤n),
(1)如果Txy≥0,那么Ju和Jv的恶化率满足bu (2)如果Txy<0,那么Ju和Jv的恶化率满足bu≥bv, 其中 证明:设最优顺序φ中Ju和Jv分别排在x和y的位置(1≤x≤l*-1,k*+1≤y≤n),将工件Ju和Jv交换位置而不改变其他工件的位置得到新加工顺序记为φ′。对于顺序φ和φ′,总目标函数值的不同之处仅在于Ju和Jv之间的目标函数值。不妨设φ中工件Ju的开始时间为t,G1(φ)和G1(φ′)分别为顺序φ和φ′下Ju和Jv之间工件的目标函数值,那么 (1+bbt),pj(φ′)=bj(a+bt)(1+bbv) 因此可计算出 G2(φ′)-G2(φ)=(bv-bu)(a+bt)Txy 那么当Txy≥0,必有bu 最优算法: 步骤1 将所有工件按照恶化率不减的顺序重新标号:b[1]≤b[2]≤…≤b[n]。 步骤2 计算l*,k*的值,将J[1],…,J[k*-l*]排在集合F∪W中,并确定E有l*-1个工件,O∪T有n-k*个工件。 步骤3 按照引理4计算Txy,并根据Txy的值来具体确定哪些工件排在集合E中哪些工件O∪T在中。 步骤4 对于集合E里的工件按照LDR顺序排列;集合O∪T中工件按SDR排列; 并计算q1和q2,以及D=q2-q1和最优目标函数值。 显然算法1对所有工件进行排序,所以它的时间复杂度为O(nlogn)。 引理5 对于任何指定的工件顺序,一定存在最优的松弛窗口满足q1=C[l*-1],q2=C[k*-1]其中1≤l*≤k*≤n,[l]代表工件被排在第l个位置。 证明:利用反证法易证,可以参见文献[12]。 根据以上分析,方程(2)可以整理为式(3) (3) 根据文献[10]中引理3~5,得到下面几个结论。 引理6 在最优排序中,集合E、F∪W和O∪T中的工件可以任意排序。 引理7 在最优排序中,集合E和F∪W中的工件的恶化率需要满足以下条件: (1)如果γ≥δ,那么集合E中工件的恶化率都要小于集合F∪W中工件的恶化率; (2)如果γ<δ,那么集合E中工件的恶化率都要大于集合F∪W中工件的恶化率。 引理8 在最优排序中,集合F∪W中的工件的恶化率要小于集合O∪T中工件的恶化率;集合E中工件的恶化率要小于集合O∪T中工件的恶化率。 推论1:在最优排序中,集合E、F∪W和O∪T中工件的恶化率满足: (1)如果γ≥δ,集合间恶化率顺序为E→F∪W→O∪T; (2)如果γ<δ,集合间恶化率顺序为F∪W→E→O∪T。 最优算法: 步骤1 按照恶化率的大小重新对工件进行标号b[1]≤b[2]≤…≤b[n],令开始时间为t0=0。 步骤2 先令E、F∪W、O∪T为空集。再令l*从1到n进行取值,k*从l*到n进行取值,对于每一个组合(l*,k*),如果γ≥δ,将转到步骤3,如果γ<δ,将转到步骤4。 步骤3 将J[1],…,J[l*-1]排入E中,将J[l*],…,J[k*-1]排入F∪W中,将剩余的工件加入O∪T,再按照公式(3)计算出目标函数值。 步骤4 将J[1],…,J[k*-l*]加入F∪W中,将J[k*-l*+1]…J[k*-1]加入E中,再将剩余的工件加入O∪T,最后按照公式(3)计算出目标函数值。 步骤5 选择目标函数值最小的组合(l*,k*)即可,并计算q1、q2和D值。 由于考虑(l*,k*)的所有可能组合,显然算法2的时间复杂度为O(n3)。 本文研究单机更一般线性恶化的松弛窗口排序问题,给出解决问题的多项式时间算法。可以将本文的结果进一步拓展到不同工期窗口排序问题,并可以考虑将单机问题推广到平行机问题中。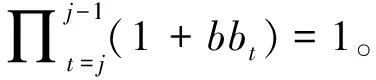

2.3 最优求解算法

3.1 基本结论

3.2 最优的工件加工顺序
3.3 最优求解算法
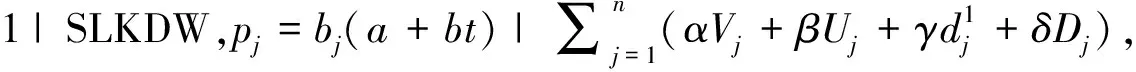
4 结论
