基于K-means算法的故障电弧检测方法

张 帅，曲 娜，郑天芳，胡从强,李玮祯

(沈阳航空航天大学 安全工程学院，沈阳 110136)

作为最便捷的能源,电能在生产生活中起着至关重要的作用。近年来，随着电能在各领域的广泛应用，因电气设备或输电线路发生故障而引起的火灾等事故给人们的生命财产造成了极大的损失。据统计，此类事故中由于故障电弧引发的火灾占了近30%，传统的低压断路器和剩余电流断路器对故障电弧的识别能力较差，在故障电弧发生时不能及时切断电路。因此对于故障电弧的检测和其断路器的研究有着重要的意义。

人们对故障电弧的研究以改进模型、改变故障特征值的提取和算法优化为主，但低压电力系统中负载类型的复杂性会很大程度上影响特征提取和检测。本文对Cassie电弧模型下不同负载进行了仿真研究，使用快速傅里叶算法分析了不同负载条件下电弧故障的时频特点，并使用K-means算法，以单相桥式整流电路这一常见非线性电路为例，对正常与故障下电流频谱的相关特征值进行了聚类分析，实现了电弧故障检测。

国外学者对于故障电弧的研究主要是基于电弧产生时的光、热等物理特性，目前常用的有Cassie和Mayr电弧模型[1-2]。在复杂负载和电压环境下两种模型有各自的局限性，文献[3]提出了一种可以弥补经典电弧模型在感性负载下特性缺失的改进Mayr电弧模型。文献[4]引进遗传算法提出遗传优化的高斯混合模型(GA-GMM)。故障电弧检测研究的问题主要集中于故障特征的提取和检测算法的优化。电流和电压的时域波形在故障发生时通常会产生不规则的振荡，检测时难以提取固定的特征值，因此特征值通常取频域的相关参数。傅里叶变换和小波变换是常用的时频变换方法，文献[5]对大量的线性和非线性负载进行试验,提出了快速傅里叶分析法(FFT)和小波变换法检测故障电弧。文献[6]对常用的传统快速傅里叶分析法(FFT)无法同时保证时频精度的问题进行了改进，提出了Cassie故障电弧模型的小波分析检测方法。文献[7]进行了Cassie模型下的快速傅里叶分析和小波分析，并使用神经网络对特征值进行了提取。文献[8]提出了一种基于单片机和Mayr电弧模型的平稳小波变换法，提取电弧波形的平肩比例和奇异值为特征值对故障电弧进行检测。文献[9]在快速傅里叶变换和小波变换的基础上提出了一种深度特征优化方法并使用增强型自动编码器从大量的数据中提取特征。近年来模式识别和深度神经网络的兴起将特征提取与检测进行了融合。文献[10]开发了一种基于时间序列分解和长期短期记忆网络(LSTM)的独特方法并设计了一种架空导体上放电现象的模式识别方式。文献[11]采用小波变换与信息熵相结合的方式提取了故障电弧的特征，并使用三层BP神经网络进行训练与测试。文献[12]利用基于 L3/4 范数正则化的稀疏算法对小波分析下提取的故障电弧特征值进行训练和测试。文献[13]采用集合经验模态分解(Ensemble Empirical ModDecomposition，EEMD)对故障电弧本征模态进行了提取，用Levenberg-Marquard(LM)算法优化的BP神经网络来进行故障电弧识别的研究，并应用于航空故障电弧的检测。文献[14]提出了一种基于 AlexNet 深度学习网络的低压串联故障电弧检测方法。通过以上文献分析，目前对于故障电弧的研究以改进模型、改变故障特征值的提取和算法优化为主，但低压电力系统中负载类型的复杂性会很大程度上影响特征提取和检测。本文对Cassie电弧模型下不同负载进行了仿真研究，使用快速傅里叶算法分析了不同负载条件下电弧故障的时频特点，并使用了K-means算法以单相桥式整流电路这一常见非线性电路为例，对正常与故障下电流频谱的相关特征值进行了聚类分析，实现了电弧故障检测。

1 Cassie电弧模型

当电弧故障发生时，电路的某些时域和频域特性通常会发生改变，通过仿真实验可以对其进行探究。

电弧的产生与环境的物理因素有着必然的联系，在电弧产生时电极之间的空间会由绝缘的空气突变为带电等离子体。

Cassie通过研究发现电弧的变化与电极间隙气体等离子柱的能量平衡有关，并通过大量实验总结出一阶常微分方程形式的电弧模型,如式(1)所示。

(1)

式(1)中：g是电弧电导，u是电弧电压，τ是电弧常数，UC是电弧电压常量。

根据式(1)所示的微分方程建立仿真模型如图1所示。

图1 Cassie电弧仿真模型

其中微分方程编辑器用于模拟Cassie电弧的数学模型，阶跃输入为1，控制电流源的初始值设置为1 A。

将图1所示的电弧模型分别与100 Ω纯电阻电路，100 Ω、0.002 2 H阻感串联电路，两个30 Ω电阻并联电路串联。以100 Ω纯电阻为例，建立电弧仿真测试电路如图2所示。

图2 串联电弧故障测试电路

其中交流电压源参数为220 V、50 Hz,将采样时间设置为0.08 s，运行仿真可以得到3组测试电路的电流输出波形如图3～图5所示。

图3 100 Ω纯电阻串联电弧故障仿真电流波形

图4 300 Ω、0.022 H阻感串联电弧故障仿真电流波形

图5 530 Ω并联电阻串联电弧故障仿真电流波形

从3组测试电路的电流波形中不难看出，加入了Cassie电弧模块后电流波形在过零处出现了明显的平肩现象，与电路正常运行时的平滑正弦波形有着明显的区别，这种现象被称为“零休”现象，是判断线性负载电弧故障的一个重要依据。

将3组测试电路分别进行快速傅里叶变换分析可以得到3组测试电路的频谱如图6～图8所示。

图6 100 Ω电阻测试电路电流频谱

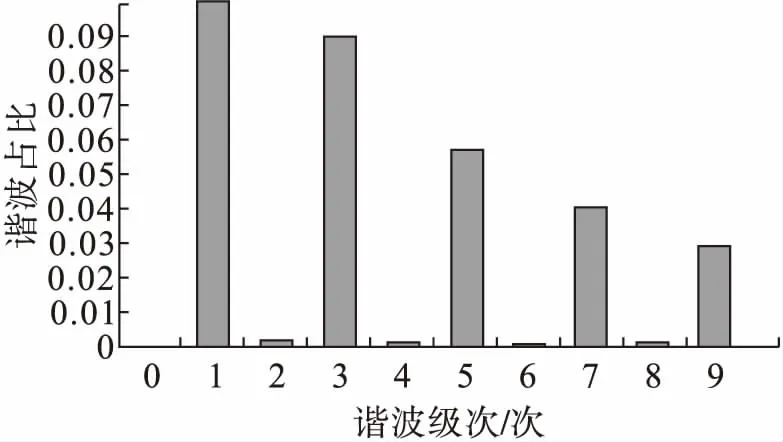
图7 300 Ω、0.022 H阻感测试电路频谱

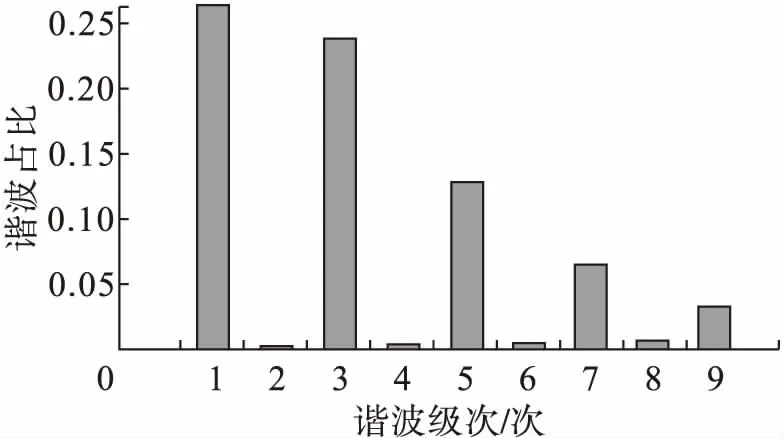
图8 30 Ω、30 Ω电阻并联测试电路电流频谱

从3组测试电路的频谱可以看出，与正常工作时只存在基波相比，在加入故障模块后3组测试电路的电流均出现了一定的奇数高次谐波。这种现象也可以作为判断线性负载是否产生电弧故障的一种依据。

2 单相桥式整流电路电弧故障仿真

对白炽灯、加热设备、变压器等阻抗不变的线性负载电弧故障检测相对容易，而为了实现更复杂的功能民用电气设备往往会加入复杂的非线性电路负载。本文对非线性负载举例进行了仿真研究，探究其在发生电弧故障时是否具有和线性负载相同的性质。

电力电子电路是常见的非线性电路，近年来随着电力电子技术的发展，越来越多的电力电子电路被广泛应用到电气工程的各个领域。整流电路是电力电子技术中发展最早、技术最成熟的一种，它的作用是将交流电转换为直流电用以供应直流电气设备。在生活和生产中整流电路无处不在，如充电器、LED灯、电脑的电源适配器等，工业生产中直流电机、发电机励磁及路由器等通信设备的供电都需要进行交流与直流的转换。整流电路按器件与原理可分为全控、半控、不可控、相位控制和斩波控制等。本文以常用的单相桥式全控整流为例仿真研究其发生电弧故障时的检测。

根据单相桥式全控整流电路的原理设计了如图9所示的仿真电路，并在变压器二次相输入端加入电弧模型[15]。

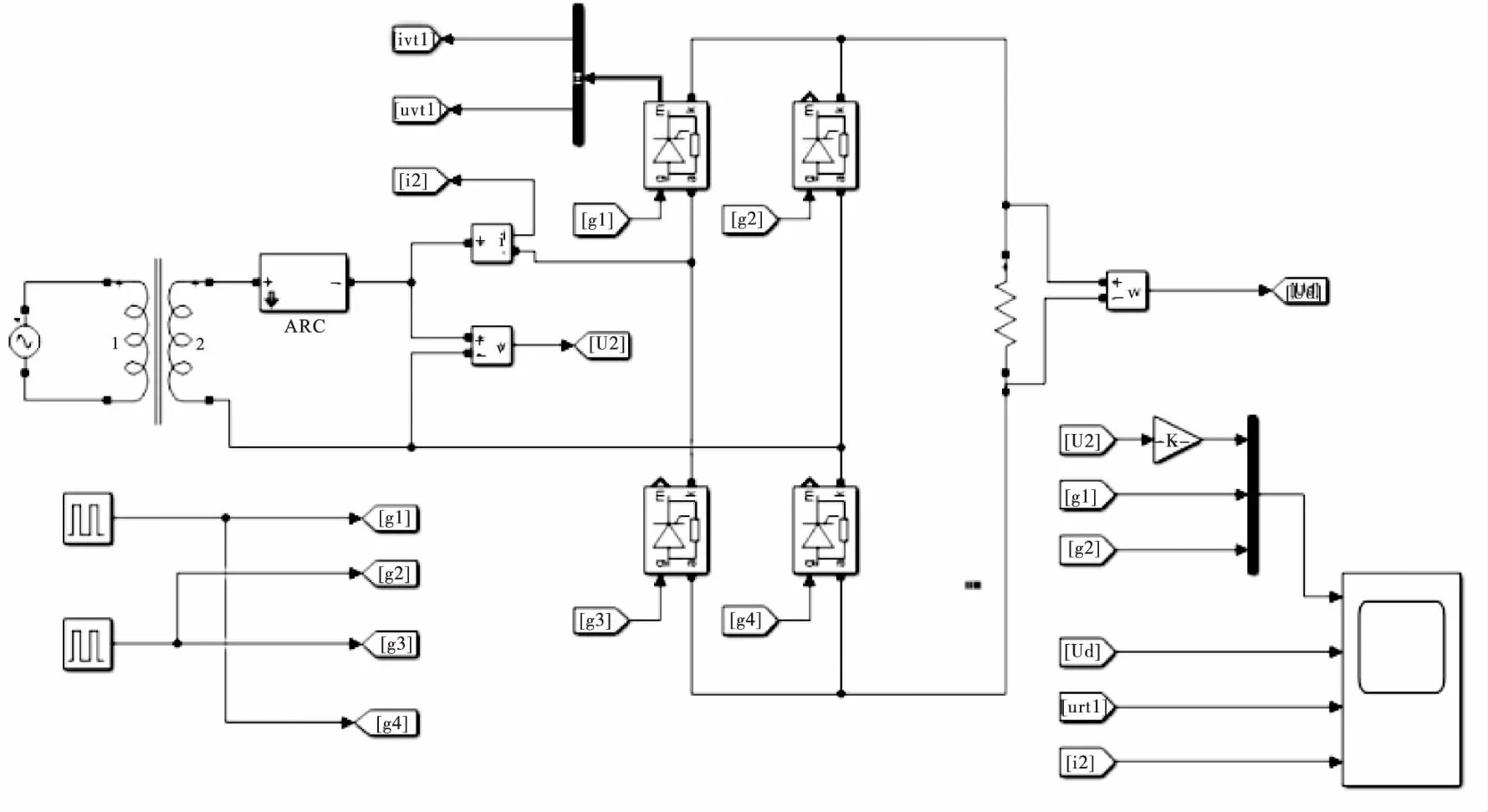
图9 单相桥式全控整流电路故障仿真

通过改变脉冲触发器相位将整流电路的延迟触发角设置为60°，将晶闸管缓冲电路内阻设置为500 Ω，电容0.25 μF，负载侧选择使用1 000 Ω的电阻。变压器二次项电压有效值220 V，频率50 Hz，采样时间0.08 s，可以得出整流电路正常运行时的交流输入端电流以及负载两端的电压波形和晶闸管电压，如图10所示。

图10 正常工作下的整流电路波形

对单相桥式整流电路进行快速傅里叶分析可以得到如图11所示的频谱图。

图11 正常工作时整流电路频谱

通过正常工作时的频谱可以看出，频谱中存在奇数高次谐波，因此频谱不能再作为判断整流电路这种非线性电路发生电弧故障的依据。在加入Cassie电弧故障模型后输入端电流波形如图12所示。

图12 单相桥式整流电路电弧故障电流波形

从电流波形看，故障波形与正常运行波形之间不能看出明显的“零休”现象，因此“零休”现象也不能作为判断整流电路发生电弧故障的依据。

3 基于K-means算法的电弧故障检测

生活中的电气设备负载类型同时包含了线性和非线性两种，而两种类型的负载在发生电弧故障时有着不同的时频特性，因此对于电弧故障的检测不能一概而论。机器学习算法在数据分类、预测、函数的线性拟合等领域有着很好的表现，检测电路的正常运行与发生故障可以视为分类问题的一种。将故障发生时的某类特征与机器学习算法相结合为实现非线性负载的电弧故障检测提供了可能。

3.1 无监督学习

无监督学习是机器学习的一种，用于解决那些因缺乏先验知识而导致的数据难以进行人工标注类别或人工标注类别成本较大的问题。聚类算法作为一种使用较多的无监督学习算法，其作用是将数据通过运算分为若干种类，其本质是寻找无标签数据的特征以区别样本数据的不同种类[16]。

3.2 K-means算法原理

K均值聚类算法(K-means Clustering Algorithm)是一种常见的无监督学习。其原理是首先随机设置K个样本为K个类别的聚类中心，将其称为质心，通过计算样本中的每个数据与这K个样本的欧氏距离判断与质心的相关度，进而将其隶属于相关度最高的质心，该质心也会随着新样本的加入重新计算直至迭代完成或到达设置好的迭代次数结束[17]。其中样本间的欧氏距离见式(2)。

(2)

式中Di表示欧氏距离，Ci,j表示样本中数据的位置，xj表示质心位置。聚类的目标函数J见式(3)。

(3)

由质心ci求导可得到新的质心如式(4)所示。

(4)

式中mk是质心数，新的质心坐标迭代至设定的最小值时迭代结束，所得的质心坐标即为最终结果。

3.3 特征值提取和参数设置

由于正常与故障情况下的电流波形均为离散序列，因此采用离散傅里叶变换(DFT)进行数据处理。由于正常使用中的电流数据量较大，为保证电弧故障的检测具有一定的实时性，采用了快速傅里叶变换(Fast Fourier Transform，FFT)进行仿真波形的时域频域变换，以提高变换效率。本文使用快速傅里叶算法对采集的电流信号频谱进行分析，并提取奇数高次谐波的幅值作为电流信号的特征值。

本文选取整流电路正常和故障情况在不同负载阻值下的奇数高次谐波幅值占基波百分比为特征值。其中负载电阻设置为30～1 000 Ω之间的随机35个阻值，得出故障和正常情况下共70组数据。数据组成为5维数组[X1,X2,X3,X4,X5]，其中X1～X4分别表示每一组数据的3次、5次、7次、9次谐波幅值的基波百分比。X5为数据的标签位，正常工作的数据设置为normal，故障的数据设置为fault，用于后续检测分类精度[18]。

3.4 算法设计和精度测试

为了便于直观观察分类的效果，将4维谐波幅值数据分别两两组合、三三组合制成二维坐标系和三维坐标系，可得二维坐标系6个，三维坐标系4个，如图13～14所示。通过K-means算法分类后可将原数组分类为故障或正常信号并生成新的标签位。精度测试的原理是对比输入数据的标签位与算法计算后的数据标签位，若相同则返回1，不同则返回0。通过计算返回数据中0的比例计算每一个坐标系下的数据分类精度。本文以此方法进行测试，试图找出以某两维或某三维奇数高次谐波占基波幅值分量为特征带入K-means算法可得出的最高聚类精度，并将其作为K-means算法检测电弧故障的最终数据特征。

图13 二维坐标系下的K-means分类结果

图14 三维坐标系下的K-means分类结果

经过精度测试后得出，70组数据在所有的坐标系下分类的精度均为100%，但从图中可以看出有一些数据偏离了聚类质心，这说明分类存在一定的误差。由于K-means聚类算法对于数据的离群点和孤立点较为敏感，在迭代过程中对于离群点，存在无法识别即输入与输出相同的情况，从而影响了精度算法的判别。在算法的编写时设置了随机的样本作为初始点，这可能会导致初始点被设置为离群样本，使聚类结果出现偏差。K-means算法面对凸样本集具有较好的聚类效果，在面对有较多离群点的样本时尚存在改进空间。

4 结论

Cassie电弧模型在串联线性负载时可以通过“零休”现象和高次谐波分量的变化来判断电路是否有故障发生，在负载为非线性负载时谐波分量和“零休”现象不再可以作为判断电弧故障的依据。K-means算法可以对非线性负载电弧故障与正常运行的电流特征值数据进行分类以达到故障准确检测的目的。以3次至9次的奇数高次谐波占基波百分比分别两两组合、三三组合作为数据特征，在70组测试数据的情况下分类准确率均为100%。这表明以上组合方式具有相同的测试精度，均可以作为K-means算法聚类检测的特征值，且在高频和低频下具有一定的普适性和实时性。