空间站空空支架天线抗力学环境设计与仿真分析*
2022-03-16师雪丽刘建坤南江红唐启敬
师雪丽,刘建坤,南江红,唐启敬,罗 鹏
(上海航天电子技术研究所,上海 201100)
引 言
建设空间站是中国载人航天工程的重要目标之一,核心舱是中国空间站的控制和管理中心,来访飞行器在核心舱统一调度下相互协同工作,完成空间站承担的各项任务。空空支架天线作为测控与通信分系统的重要组成部分,担负着核心舱与来访飞行器之间的通信任务,发射时处于收拢状态,固定在核心舱舱壁上,核心舱入轨飞行稳定后,在地面控制中心遥控下展开到位并锁定。
空间机构产品在发射、入轨后展开及在轨运行期间将经受各种严酷的力学环境考验,其抗力学环境设计直接影响航天器的总体设计,是决定航天任务成败的关键因素,因此结构设计时必须充分考虑力学环境条件的要求[1-2]。文献[3]研究了静态星载电子设备在加速度过载、振动、冲击等工况下的结构响应和受力情况,保证结构设计满足环境要求;文献[4]对空间站柔性展开机构进行了仿真研究,为我国空间站大型柔性太阳电池翼的设计提供分析参考;文献[5]对空间大型可展开天线展开机构进行了设计分析,得出了理想的结构形式。目前对空间机构产品从发射到在轨运行全任务段的载荷分析较少。
空空支架天线全行程段载荷工况包含发射段、入轨段、交汇对接段和分离段4个任务剖面。在发射段,产品为收拢状态,主要承受核心舱发射时的振动、冲击载荷;入轨后,产品展开,将承受展开到位时的冲击载荷;核心舱与来访飞行器对接、分离时,产品将承受对接分离时的冲击载荷。本文根据每个任务剖面的力学环境条件完成其全任务段的载荷分析,确定空空支架天线结构方案的可行性和力学环境适应性,对其后续详细结构设计提供依据。
1 仿真模型的建立
利用有限元分析计算锁紧态下空空支架天线的固有频率及各振动工况下的应力,对其结构刚强度予以验证。进行有限元计算时,根据空空支架天线的结构特点,对其模型的一些细节做了适当的简化,忽略小孔、圆角、倒角、凹槽等结构细节。网格划分时,展开臂采用壳单元,其余零部件采用3D四面体单元。计算时,X,Y,Z坐标系定义与核心舱本体坐标系保持一致。空空支架天线锁紧态有限元模型如图1所示。

图1 空空支架天线锁紧态有限元模型
空空支架天线选用的主要材料及其特性参数如表1所示。

表1 空空支架天线结构零件材料表
2 全任务段载荷分析
2.1 发射段载荷分析
在发射段,空空支架天线收拢锁紧在核心舱的舱壁上,承受发射时的振动、冲击、加速度等载荷[6-8]。
2.1.1 模态分析
模态分析是动力学分析的基础,目的是识别出系统的模态参数,得到结构固有的动态特性,包括固有频率、模态振型和阻尼比等,找出结构的薄弱环节,为结构系统的振动分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。本文采用振型叠加法,使用Lanczos法提取特征值,计算空空支架天线的固有频率及相应的振型。
模态分析时对固定压紧释放装置与舱体及展开锁定机构与舱体连接的2个安装表面不加任何载荷。锁紧态空空支架天线系统结构的前6阶模态固有频率见表2,系统前6阶模态振型如图2所示。

表2 空空支架天线前6阶固有频率

图2 空空支架天线前6阶模态振型图
从表2可知,空空支架天线的前6阶固有频率较高,第1阶固有频率为127.6 Hz,满足系统研制中规定的整机基频不小于100 Hz的要求。有效避开了外界激励的频率,避免了与核心舱的共振。从图2可知,在约束模态下,前2阶模态对应的振型为通信天线端部的弯曲变形,第3、4阶模态对应的振型为展开臂的弯曲变形,第5、6阶模态对应的振型为天线内导体的弯曲模态。
2.1.2 正弦振动仿真分析
正弦振动分析是用来计算结构在稳态振动激励下响应的方法。在正弦振动分析中,激励载荷在频域中以显式方式定义,对应于每一个加载频率,外载荷都是已知的[9]。外载荷可以是力,也可以是强迫运动(位移、速度或加速度)。将表3所列的条件作为输入,为便于分析,将频率范围为4~10 Hz时的位移幅值转换为加速度幅值,将加速度幅值作为正弦振动的输入。

表3 正弦振动试验条件
图3为空空支架天线在X,Y,Z三轴向正弦振动载荷作用下的Von-Mises峰值应力及变形云图。在X向正弦振动载荷作用下,结构的最大应力为13.64 MPa,出现在展开锁定机构轴承安装支架处,最大变形为0.065 mm,出现在展开臂中部;在Y向正弦振动载荷作用下,结构最大应力为47.32 MPa,峰值应力出现在天线安装支架与压紧释放装置连接处,最大变形为0.578 mm,出现在天线头部;在Z向正弦振动载荷作用下,结构最大应力为23.74 MPa,最大变形为0.284 mm,峰值应力与最大变形发生位置与Y向相同。

图3 正弦振动下空空支架天线的刚强度响应
设备的结构部件应具有正的安全裕度,安全裕度Ms的计算如下:

式中:Fs为安全系数,本文取1.5;Sa为许用破坏应力,这里取钛合金的屈服极限900 MPa;Se为等效使用应力。
根据式(1),空空支架天线在X,Y,Z三轴正弦振动载荷作用下,对应的安全裕度分别为[Ms]X ≥42.9,[Ms]Y ≥11.7,[Ms]Z ≥24.3,安全裕度满足设计要求,说明空空支架天线结构设计的刚强度满足正弦振动环境要求。
2.1.3 随机振动分析
随机振动试验条件见表4。在模态分析的基础上,运用模态叠加法,取临界阻尼0.03,将表4所示的试验条件作为载荷输入,计算空空支架天线在X,Y,Z向随机振动激励下的响应。

表4 随机振动试验条件
图4为3个方向随机振动激励下的Von-Mises峰值应力和变形云图。在随机振动激励下,X向Von-Mises均方根应力最大值为11.94 MPa,出现在展开锁定机构轴承安装支座处;Y向Von-Mises均方根应力最大值为13.48 MPa,出现在天线安装支架与压紧释放装置连接处;Z向Von-Mises均方根应力最大值为14.26 MPa,也发生在天线安装支架与压紧释放装置连接处。X向的最大位移分别为0.150 mm,出现在展开臂中部;Y,Z两个方向的最大位移分别为0.455 mm和0.320 mm,均出现在天线头部。

图4 随机振动下空空支架天线的刚强度响应
根据式(1),空空支架天线在X,Y,Z三轴随机振动载荷作用下,对应的安全裕度分别为[Ms]X ≥49.3,[Ms]Y ≥43.5,[Ms]Z ≥41.1,安全裕度满足设计要求,说明空空支架天线结构设计满足随机振动环境要求。
2.1.4 加速度响应分析
加速度过载是空间设备在发射过程中需承受的重要动力学环境之一。空空支架天线的加速度过载试验条件见表5。由于加速度激励载荷维持时间较长,而且其变化符合线性规律,因此可将加速度过载看成一个近似准稳态过程,直接采用静力分析法进行分析[10-11]。

表5 加速度试验条件
进行加速度分析时,在空空支架天线展开锁定机构及压紧释放装置安装底板处分别输入X,Y,Z向的加速度载荷,空空支架天线的变形及应力云图如图5所示。从图5可以看出,当加速度沿3个方向过载时得到的变形分别为0.204 mm,0.094 mm和0.038 mm,都小于天线到舱壁的距离15 mm。Z向过载时的Von-Mises应力最大,为44.32 MPa,出现在压紧释放装置的座块上(该零件材料为钛合金)。根据公式计算,在该工况下结构的安全裕度Ms=12.5>0,表明系统在此工况下是安全的。

图5 加速度过载下空空支架天线的刚强度响应
2.2 入轨段载荷分析
核心舱入轨飞行稳定后,地面控制中心遥控空空支架天线展开到位并锁定。展开过程为无源展开,依靠转轴处的扭簧为机构展开提供动力,锁紧装置中的压簧又提供一定的阻尼,以减缓展开速度,使展开过程平稳,如图6所示。这个阶段承受的载荷为展开到位时的冲击载荷。

图6 展开锁定机构展开到位图
将空空支架天线的模型导入Adams中,按表1对运动零件赋予材料属性,所有转动副和滑动副的摩擦系数取0.1(运动面均喷涂二硫化钼固体润滑),主要接触定义为刚体之间的接触。设置重力为0,对展开过程进行机构动力学仿真,扭簧刚度为17.6 N·mm/(°),初始扭转角为114°,初始扭矩为2 006.4 N·mm;锁定压簧刚度为1.73 N/mm,初始压缩距离为10.7 mm,初始预紧力为18.5 N。展开到位时凸轮与挡块的冲击力变化曲线见图7(a),最大撞击力约为2 600 N,接触面积为100 mm2,计算应力为26 MPa,远小于铝合金的破坏强度极限。凸轮与锁定滚轮之间的冲击力变化曲线见图7(b),最大撞击力约为280 N,小于滚轮轴承的额定负荷(额定动负荷为1 080 N,额定静负荷为440 N),因此在整个展开过程中设备是安全的。

图7 凸轮与挡块、滚轮的碰撞力随时间变化曲线
2.3 交汇对接段、分离段载荷分析
在交汇对接段和分离段,空空支架天线将承受空间站与来访飞行器交汇对接、分离时产生的冲击载荷(表6),其安装位置见图8。

图8 空空支架天线安装位置图

表6 交汇对接、分离冲击载荷
产品转动部分的质量m= 2.62 kg,转动惯量J= 1.12 kg·m2,质心与转轴中心的距离L=0.557 m。逆时针扭矩为负,顺时针扭矩为正。展开到位时,扭簧的剩余扭转角度为15°,则剩余的保持力矩Ma= 0.264 N·m。X轴上的角加速度载荷和Y轴、Z轴上的加速度载荷将会在转轴上产生扭转载荷,当扭转载荷大于扭簧的剩余扭矩时,支架天线将会发生摆动。
X轴角加速度载荷在转轴处产生的扭矩M1为:

式中,ε为X轴角加速度。
代入数据得M1=-1.12×1.221 5=-1.368 N·m。Y轴、Z轴上的加速度载荷在转轴上产生的扭矩M2为:
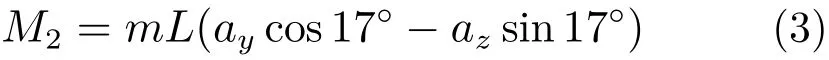
式中:ay为Y轴上的加速度;az为Z轴上的加速度。
代入数据得M2= 2.62× (1.023 1× cos 17°+0.148 4×sin 17°)×0.557 = 1.491 N·m。因此,由对接、分离载荷产生的转轴处的扭矩M=M1+M2=-1.368+1.491=0.123 N·m。
由以上分析可知,对接、分离载荷产生的转轴处的扭矩与扭簧剩余保持力矩方向相同,因此核心舱与来访飞行器对接、分离时,空空支架天线均不会发生摆动。
3 结束语
本文对空空支架天线进行了全任务段载荷分析,通过有限元分析、机构动力学仿真和计算校核,对每个任务段的载荷进行了充分论证,并已完成试验验证和工程应用,结构设计满足力学环境要求。
从对发射段的加速度过载、正弦振动和随机振动进行的仿真分析可知,结构强度足够,安全裕度最小为11.7,远大于指标要求。在下一步研究中将进行轻量化设计。
通过对在轨展开过程进行机构动力学仿真,得出凸轮与挡块、滚轮轴承的碰撞应力,满足安全裕度要求。在下一步研究中将通过合理匹配、多轮迭代,找出驱动扭簧和阻尼压簧的最佳初始值,使展开过程平稳、冲击小。
通过对交汇对接、分离段载荷进行计算校核,得知空空支架天线在核心舱与来访飞行器对接、分离时姿态稳定,不会发生摆动。在下一步研究中,将结合全行程段载荷分析,使扭簧剩余保持力矩最大化。
