警用防暴盾牌低能量冲击数值模拟与试验研究

2022-03-16王希阔周克栋任海钺

兵器装备工程学报 2022年2期

李硕，王希阔，周克栋，赫雷，陆野，任海钺

(1.南京理工大学机械工程学院，南京 210094； 2.吉林白城平台108信箱，吉林白城 137001)

1 引言

警用防暴盾牌主要是用来压制暴徒、掩护后排、抵御非爆炸性投掷物和尖锐器械冲击的单兵护体防御器具[1-2]。本文中选取的警用防暴盾牌的外形如图1所示，该警用防暴盾牌主要是用聚碳酸酯(PC)注塑成型，这种高分子材料具有良好的冲击韧性，稳定性好，绝缘性能也很好，不易燃烧，能够有效承受外界载荷。另外，盾牌外包橡胶包边条，背面装有双握把，方便双手握持，以此抵抗外界冲击。防暴盾牌的抗冲击性能要求是保证防暴人员安全的重要前提。

目前防暴盾牌的研究只局限于材料方面的本构模型研究[3-7]，对于防暴盾牌本身的结构的冲击力学响应性能的研究较少。本文中基于ABAQUS软件进行防暴盾牌的建模与仿真，研究其在不同条件下的冲击动力学特性[8]并通过试验验证仿真结果的准确性。

图1 警用防暴盾牌

2 低能量冲击理论及材料本构模型

2.1 低能量冲击理论

冲击试验的机理是在极短时间内将外力通过预计途径施加到受力件上，使其状态发生突变并产生冲击响应，此过程中的最大加速度和最大受力体现了受力件的力学性能。冲击类型根据冲击速度可分为低能量冲击、高能量冲击以及超高能量冲击，当冲击速度小于25 m/s时，则属于低能量冲击[9]。

基于落锤冲击试验机对警用防暴盾牌进行低能量冲击是一个瞬态的动力变化过程[10]。在此过程中，盾牌产生应力波的传播和结构动态响应，引发结构非线性与材料非线性等问题。而ABAQUS/Explicit模块能很好地解决各种非线性问题，并能很好地求解结构的动态响应以及冲击过程中相关能量的变化[11-12]。

根据有限单元法基本理论可知[13]，系统的动力学特性方程为：

(1)

2.2 聚碳酸酯(PC)的本构模型

根据聚碳酸酯(PC)的应力应变关系可知，其满足Johnson-Cook本构模型[6，14]，也是冲击问题中常用的模型，其简化了本构模型的形式，基本表达式为：

(2)

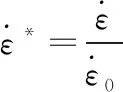
聚碳酸酯(PC)的Johnson-Cook本构模型的基本参数如表1所示[14]。

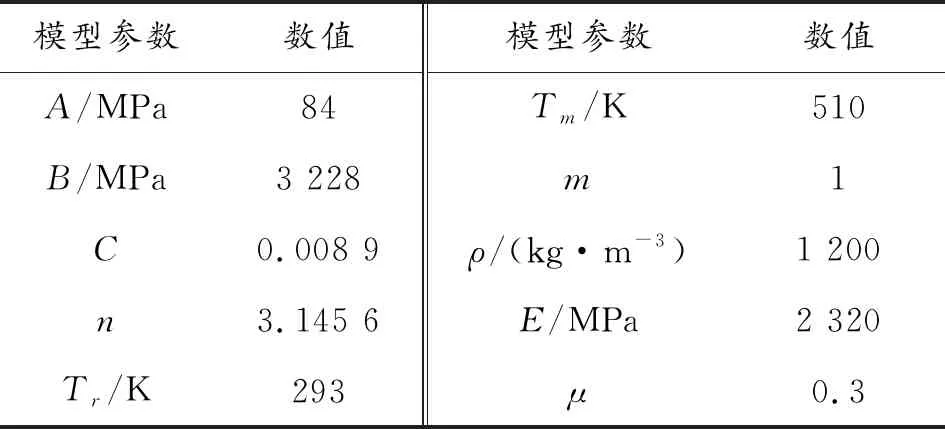
表1 聚碳酸酯(PC)材料参数

3 有限元模型

防暴盾牌为曲面造型，可在SolidWorks中建立冲击组件与防暴盾牌的装配体，然后将.x_t格式文件导入到ABAQUS的部件。坐标系如图2所示，全局施加沿着y轴负方向的重力加速度，大小为9.8 m/s2，对防暴盾牌划分网格，网格类型为六面体网格，单元类型为C3D8。锤头和防暴盾牌之间建立通用接触。防暴盾牌在冲击试验时，水平放置在冲击试验台上，因此防暴盾牌的两侧平板设置为固定约束。冲击总时间设置为0.05 s[15]。冲击指定点为盾牌的正中间。建立的警用防暴盾牌的数值分析模型如图2所示。

图2 警用防暴盾牌的数值分析模型示意图

根据GA 422—2019[16]可知，警用防暴盾牌的冲击试验主要使用直径为45 mm、质量为10 kg的半球型钢柱，自1.5 m跌落，提供147J的能量冲击防暴盾牌的指定冲击点。为了提高计算效率，忽略落锤与导轨间的摩擦和空气阻力等因素，根据能量守恒定律，有：

(3)

式(3)中：M为下落物体总质量10 kg；v为落锤第一次与防暴盾牌接触时的初速度；h为锤头的下落高度1.5 m。代入计算可得v=5.422 m/s，以初速度为预定义场初始条件。

4 仿真计算结果与分析

4.1 不同冲击能量的冲击力时程曲线

为研究不同冲击能量作用下盾牌的冲击响应，数值模型中用落锤的初速代替落锤的下落高度，将锤头分别以对应于下落高度1.0 m、1.5 m以及2.0 m的速度4.427 m/s、5.422 m/s、6.261 m/s，冲击曲率半径为450 mm，厚度为4 mm的盾牌，冲击力定义为锤头与试件之间的接触力，因此可得不同冲击能量的冲击力时程曲线如图3所示，其曲线分析如表2所示。

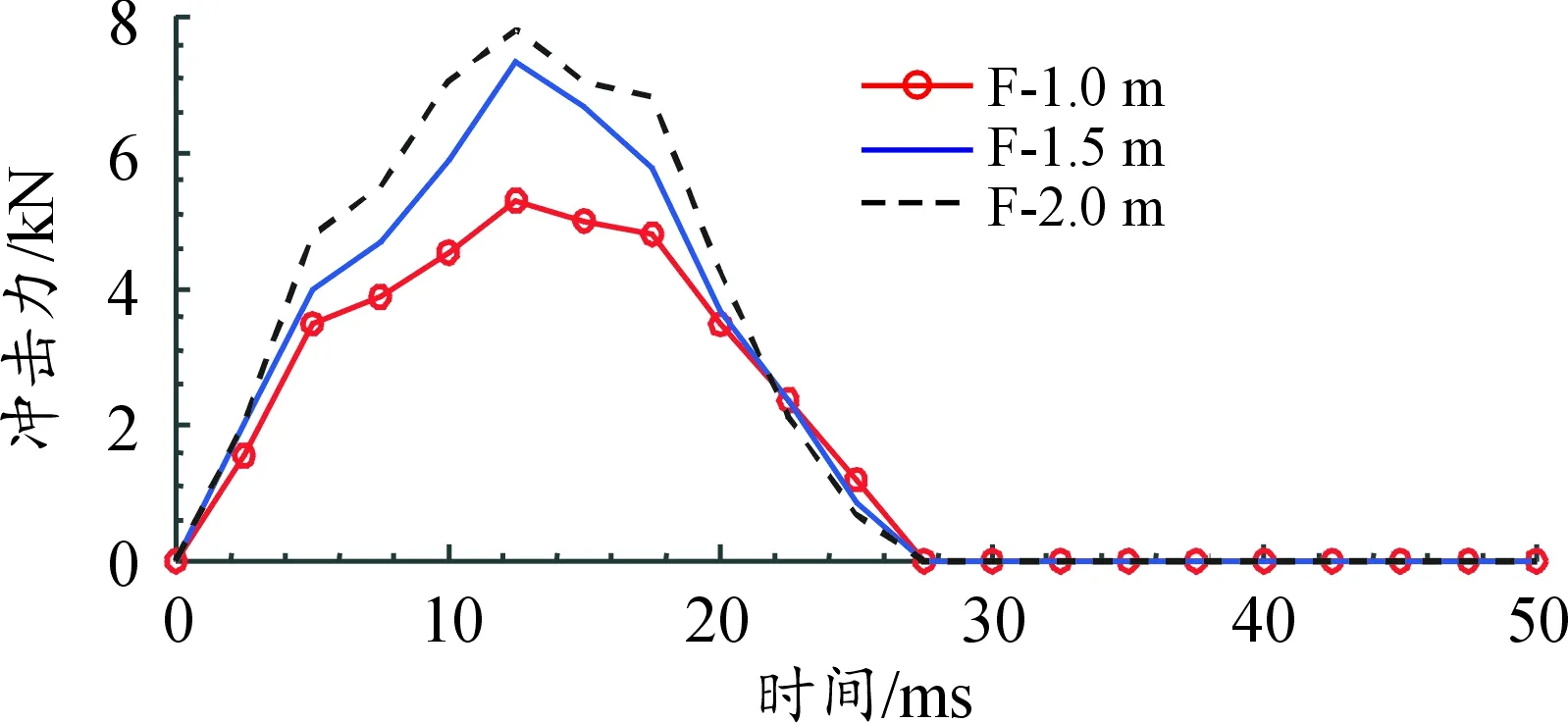
图3 不同下落高度的F-t曲线

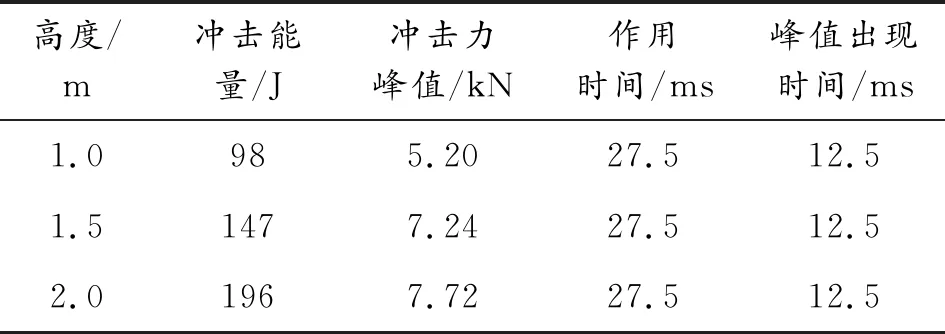
表2 不同下落高度的F-t曲线分析

根据图3、表2可知，随着下落高度增加，冲击能量增大，冲击力峰值增大，但冲击力的作用时间相近，最大峰值出现的时间相近。但在恢复阶段的后期(22～27 ms)，下落高度对冲击力几乎没有影响。

4.2 不同曲率半径的防暴盾牌

为研究不同曲率半径对盾牌的冲击响应的影响，将盾牌的曲率半径分别设置为430 mm、450 mm、470 mm以及平板盾牌，建立不同曲率半径的防暴盾牌的冲击数值分析模型，根据GA 422—2019[16]可知，锤头需要以下落高度1.5 m对应的速度5.422 m/s，冲击厚度为4 mm的盾牌，可得不同曲率半径的防暴盾牌与锤头间的冲击力时程曲线如图4所示，其曲线分析如表3所示。

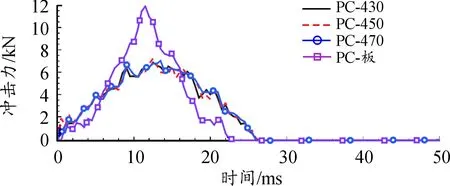
图4 不同曲率半径的盾牌的F-t曲线

根据图4、表3可知，曲面的防暴盾牌PC- 430变为PC- 450以及由PC- 450变为PC- 470，冲击力峰值分别由6.87 kN增加到7.03 kN以及由7.03 kN增加到7.24 kN，增幅分别为2.3%、3.0%。可见，在小范围内改变防暴盾牌的曲率半径，不能有效地改变冲击力峰值。但平板盾牌与曲面盾牌受到冲击后特性差异较大，比如曲面盾牌PC- 470变为平板，冲击力峰值由7.24 kN显著增加到11.90 kN，增幅达64.4%，除了冲击力峰值有显著增加外，冲击接触时间由原来的25.5 ms缩短至22.5 ms，缩短了11.8%。

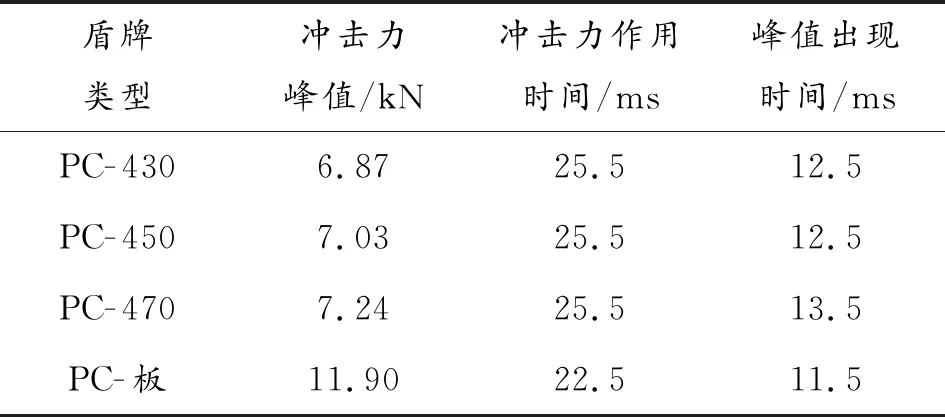
表3 不同曲率半径的盾牌的F-t曲线分析

4.3 不同厚度的防暴盾牌

为研究不同聚碳酸酯厚度对防暴盾牌抗冲击性能的影响，以450 mm曲率半径的盾牌为前提，分别将盾牌的厚度设置为2 mm、4 mm、6 mm，同样以下落高度1.5 m对应的速度5.422 m/s冲击盾牌，可得冲击力时程曲线如图5所示，其曲线分析如表4所示。

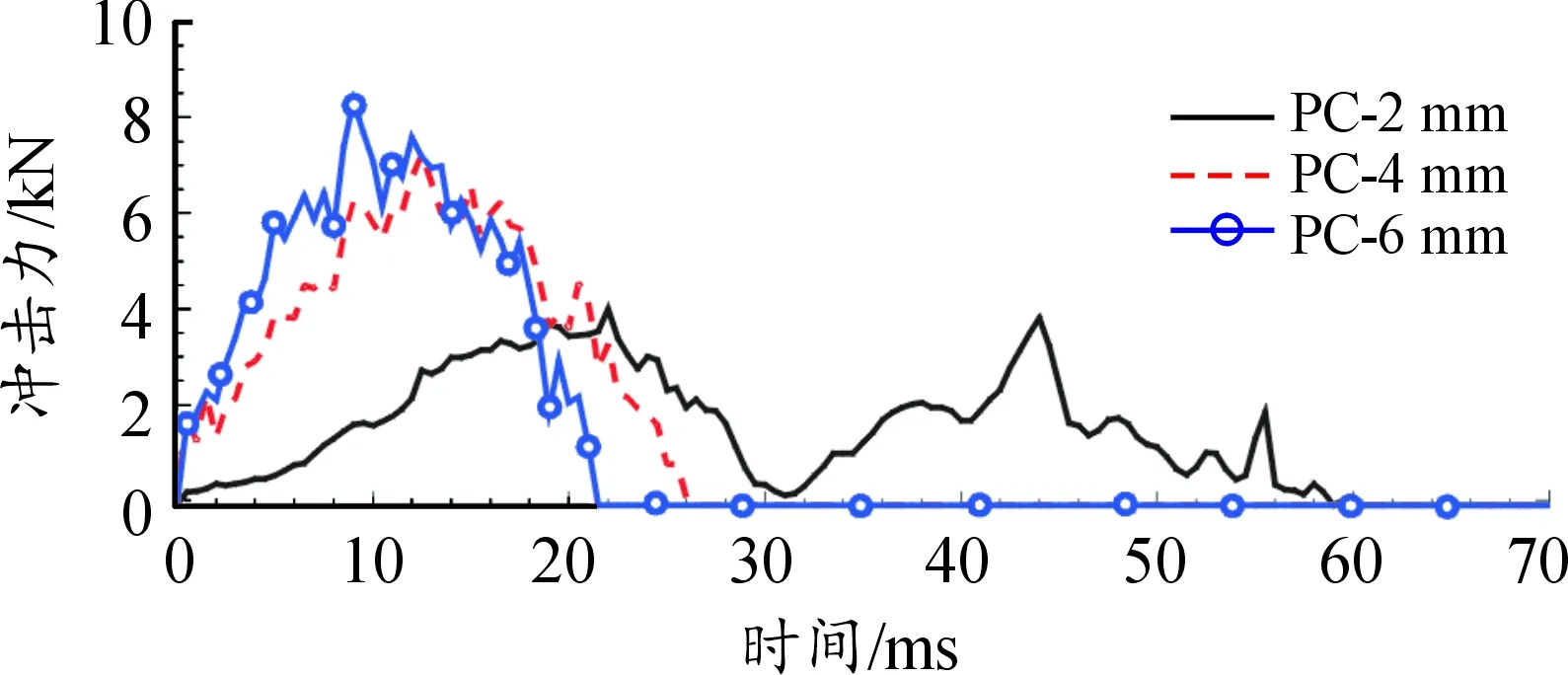
图5 不同厚度的盾牌的F-t曲线

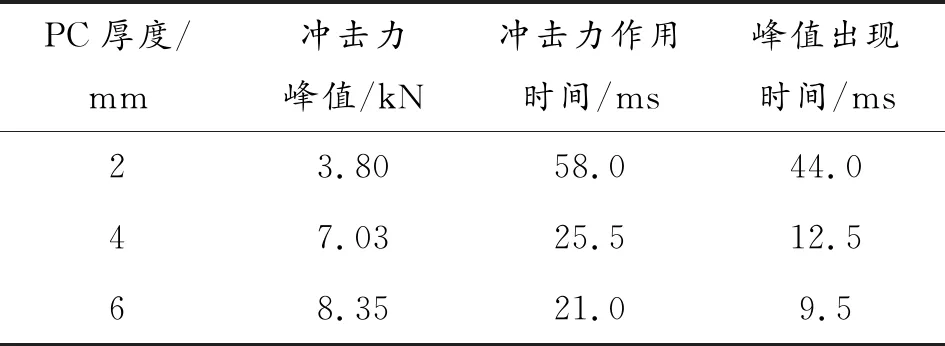
表4 不同厚度的盾牌的F-t曲线分析

根据图5、表4可知，冲击力峰值随着防暴盾牌的加厚而增大，但冲击力作用时间随着防暴盾牌厚度的加厚而减小。因为随着防暴盾牌厚度的增大，等效动力学模型中的等效刚度增大，阻尼系数减小，因此冲击力增大，冲击力作用时间缩短。当PC厚度为2 mm时，盾牌的刚度明显较小，将发生较大的弹性变形，因此PC-2 mm时的曲线出现2次明显峰值。

5 冲击试验结果与分析

5.1 测试系统搭建

为了验证上述数值仿真模型的正确性，利用总质量为10 kg的冲击组件，对材料为聚碳酸酯(PC)、曲率半径为450 mm、厚度为4 mm的警用防暴盾牌进行冲击试验。冲击试验的测试系统如图6所示。锤头被提升到指定高度自由下落，冲击试件时，锤头尾部的力传感器测得实时数据传递给电荷放大器，再经数据采集箱传递给计算机后，经过计算可得锤头与试件间的实际冲击力。

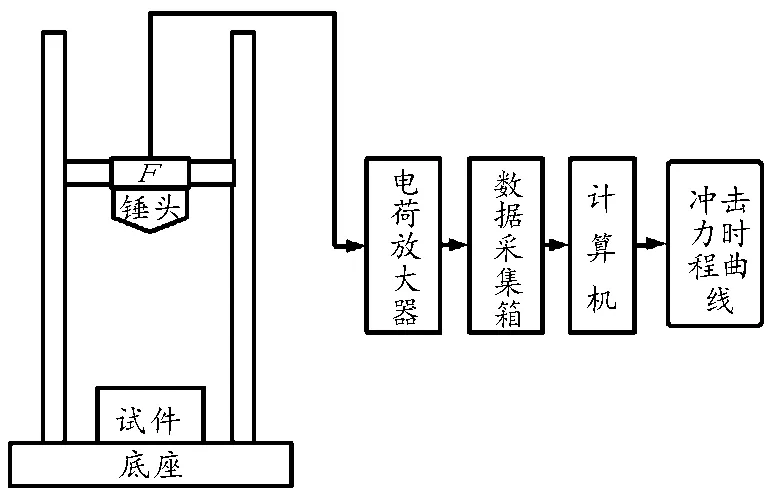
图6 冲击试验测试系统示意图

根据图6可知，冲击试验测试系统的设备主要包括：① 落锤冲击试验机；② DH5922N数据采集箱；③ DH5857-1电荷适调器；④ 美国Dytran公司1060C系列压电式力传感器；⑤ 试件—警用防暴盾牌等。

利用上述设备，搭建的试验现场如图7所示。试验中需要将10 kg的冲击组件分别提升到1.0 m、1.5 m、2.0 m，让其自由下落，冲击防暴盾牌。

1—冲击组件；2—电荷放大器；3—数据采集箱

5.2 冲击力时程曲线分析

冲击组件自1.0 m、1.5 m以及2.0 m自由下落，力传感器可测得不同的力的时程曲线。但力传感器测得的数据并不是锤头和盾牌的实际冲击力，因此需通过受力分析获得。冲击组件和锤头的受力分析如图8所示。

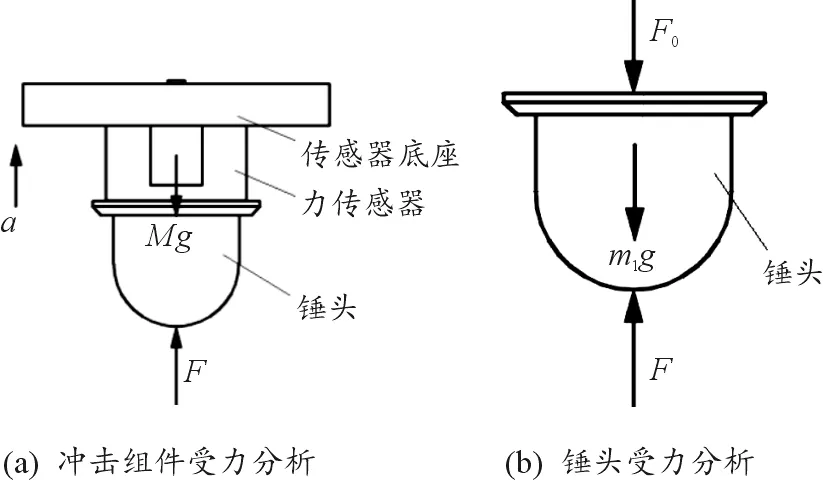
图8 冲击组件和锤头的受力分析

以冲击组件为受力分析对象可知：

F-Mg=Ma

(4)

以锤头为受力分析对象可知：

F-F0-m1g=m1a

(5)

联立式(3)与式(4)，可得落锤与试件间实际冲击力为：

(6)

式(4)～(6)中：F为锤头与试件之间的实际冲击力；a为冲击组件运动时的加速度；M为冲击组件总质量10 kg；F0为为力传感器测得的锤头与传感器之间的相互作用力；m1为锤头的质量0.5 kg。

对比试验和仿真中不同下落高度下的冲击力时程曲线如图9。

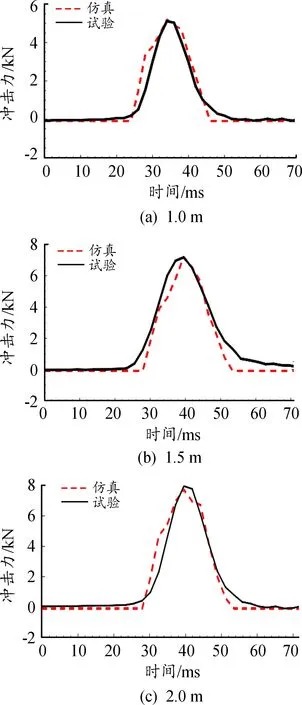
图9 仿真与试验冲击力时程曲线

根据图9仿真与试验的冲击力峰值，制定峰值误差曲线如表5所示。

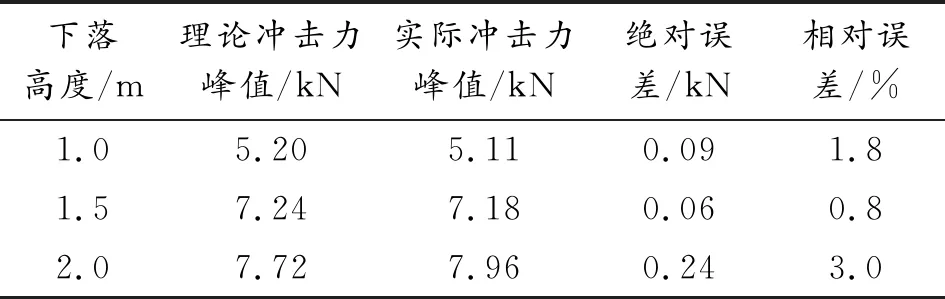
表5 仿真与试验冲击力时程曲线峰值误差

在冲击问题分析中，冲击力峰值和冲击时间是2个主要指标，根据图9、表5分析可得，冲击力峰值的相对误差小于5%，在允许的范围内。仿真和试验的冲击力的持续时间大约均在25 ms。因此利用该模型进行防暴盾牌的抗冲击性能分析是可靠的。

不同下落高度的试验冲击力时程曲线对比如图10所示，其曲线分析如表6所示。

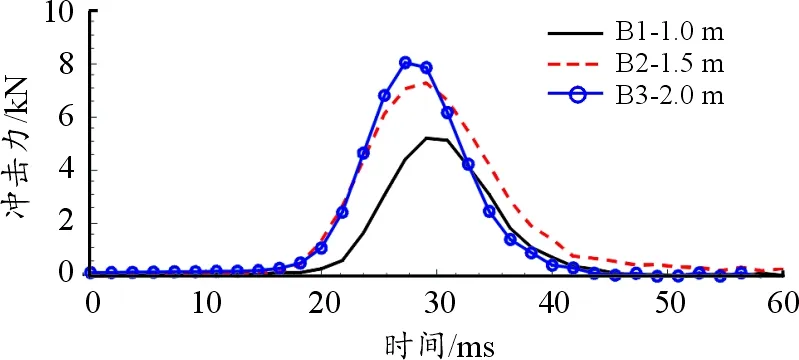
图10 试验的冲击力时程曲线

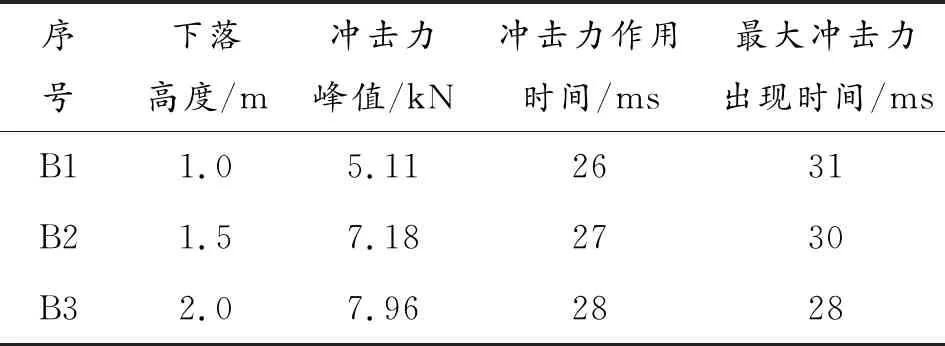
表6 不同下落高度试验的冲击力时程曲线分析

根据图10、表6可知，随着落锤下落高度的增加，落锤与防暴盾牌间冲击力峰值增大，冲击力作用时间增加，最大冲击力出现的时间提前。但B1曲线到B2曲线落锤下落高度由1.0 m增加到1.5 m，冲击能量增加了49 J，冲击力峰值由5.11 kN增加到7.18 kN，增加了40.6%。而B2曲线到B3曲线落锤下落高度由1.5 m增加到2.0 m，冲击能量同样增加了49 J，而冲击力峰值由7.18 kN增加到7.96 N，仅增加了10.9%。相同的冲击能量增量引起的冲击力变化增幅的百分比并不相同。这是由于防暴盾牌的材料为聚碳酸酯，具有很好的冲击韧性，在冲击过程中会发生大变形来吸收锤头的冲击能量，但出现冲击力峰值以后的变形速率小于冲击力峰值出现前的变形速率，因此冲击力峰值增幅会随着冲击能量的增大而减小，故B2到B3的冲击力峰值增幅比B2到B1的冲击力峰值增幅小。

5.3 落锤运动特性分析

根据牛顿第二定律，将锤头所受的合力除以锤头的质量，可得锤头的加速度时程曲线。以锤头和防暴盾牌首次接触时刻为时间起点，两者分离时刻为时间终点，首次接触点为坐标原点，向下运动方向为正方向。针对加速度时程曲线的数据，采用四阶龙格库塔法进行处理，得到图11不同下落高度的锤头的速度曲线，对速度时程曲线进行二次处理，可得图12不同下落高度的锤头位移曲线。

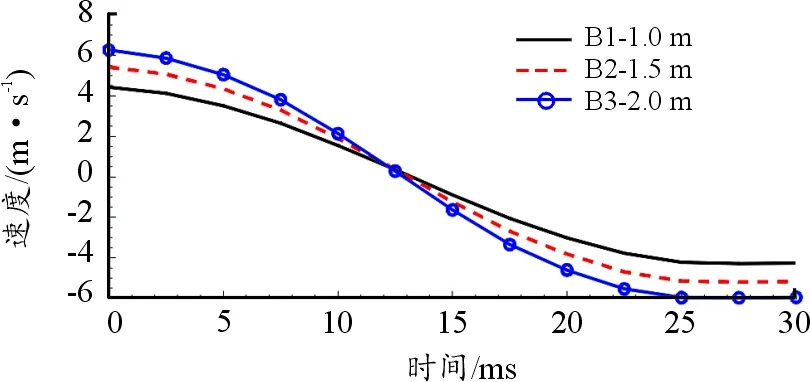
图11 锤头速度曲线

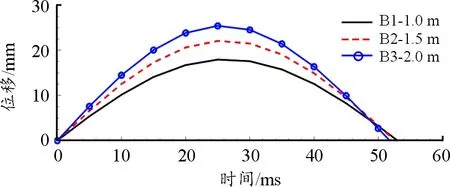
图12 锤头位移曲线

根据图11、图12，分析可得锤头运动特性如表7所示。

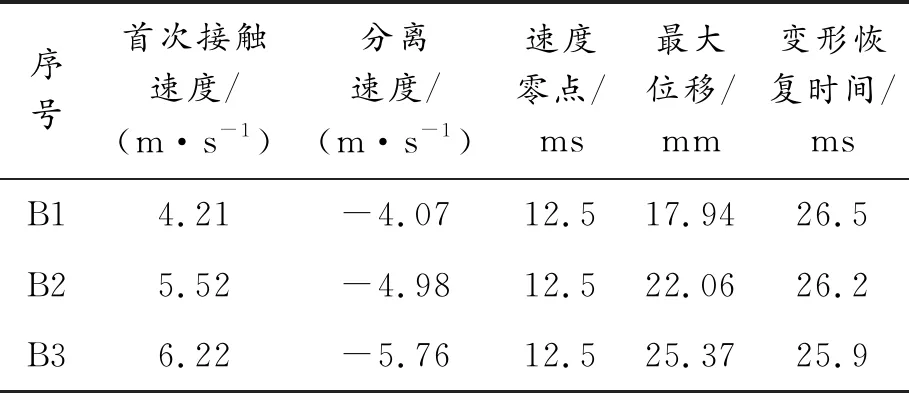
表7 锤头运动特性分析

根据表图11、图12、表7分析可得，随着下落高度的增加，锤头与防暴盾牌首次接触速度增大，分离速度绝对值增大，最大位移增大，防暴盾牌变形恢复时间缩短。由图11可知，锤头的速度零点均为12.5 ms左右，说明防暴盾牌具有较好的冲击韧性，对不同冲击能量的变形时间以及恢复时间基本相同。由表7可知，锤头与盾牌分离的速度绝对值小于首次接触速度，主要是由于在冲击过程，防暴盾牌发生塑性变形、锤头与盾牌摩擦等会消耗一部分能量。防暴盾牌的位移时程曲线几乎是关于t=12.5 ms对称的，原因是防暴盾牌的材料为聚碳酸酯，具有很好的冲击韧性，在冲击过程中以弹性变形为主，因此加载和卸载阶段的时间相近。

5.4 低速冲击能量响应分析

5.4.1冲击能量时程曲线

冲击能量公式为

(7)

式(7)中：M为冲击组件质量；v为冲击过程中冲击组件的瞬时速度大小。可得冲击能量时程曲线如图13。

根据图13可知，防暴盾牌加载过程和卸载过程曲线关于t=12.5 ms近似对称。锤头在与试件接触后12.5 ms，锤头的冲击能量达到全程的最小值0。12.5 ms后锤头在防暴盾牌弹性势能的作用下，反向运动，25 ms时弹性势能转变为锤头的动能，25 ms后锤头在重力的作用下减速，锤头冲击能量开始下降，但此时只受重力作用，因此变化较慢。

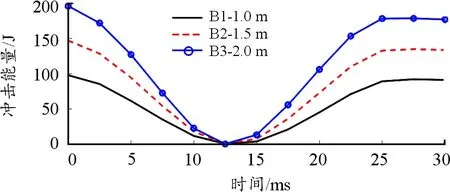
图13 冲击能量时程曲线

5.4.2防暴盾牌的吸收能量时程曲线

将上述锤头速度v和位移s时程曲线数据代入吸收能量公式，有：

(8)

式(8)中，vmax为锤头与盾牌首次接触速度，也是冲击过程的最大速度。

将上述锤头的速度v和位移s时程曲线数据以及表8中首次接触速度代入式(8)，可得试件吸收能量时程曲线如图14所示，其曲线分析如表6所示。

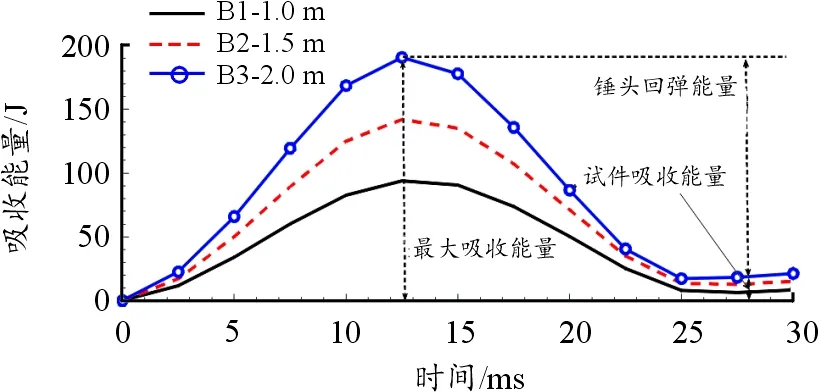
图14 试件吸收能量时程曲线

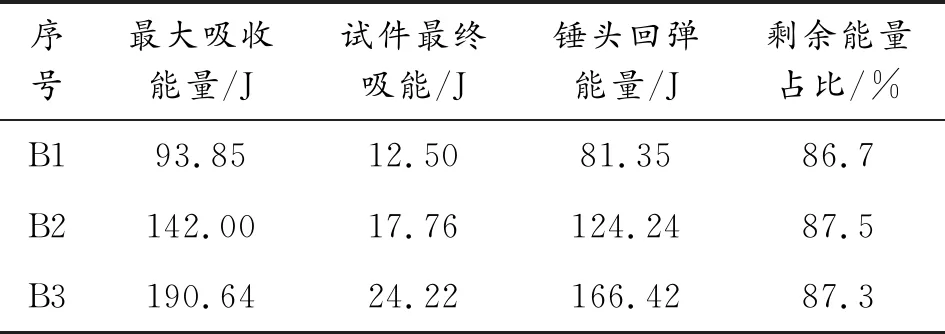
表8 试件吸收能量时程曲线分析

根据图14和表8可知，随落锤下落高度的增加，防暴盾牌最大吸收能量增加，锤头回弹的能量增大，防暴盾牌最终吸收的能量增加，但差别很小，试件最终吸收能量仅仅为冲击能量的一小部分，这一部分为防暴盾牌的塑性变形提供能量，因此盾牌塑性变形不明显。锤头回弹能量较大，这一部分回弹能量主要来自试件的弹性变形，因此试验中锤头回弹较高。剩余能量占比定义为锤头回弹能量与盾牌最大吸收能量的比值，比值大则以弹性变形为主，比值小则以塑性变形为主。试验研究表明，试验中盾牌在1.0 m、1.5 m、2.0 m等3个不同下落高度时，剩余能量占比都超过了86%，因此防暴盾牌在冲击过程中主要依靠弹性变形吸收、储存与释放能量。