断层几何形态和自发破裂的动力学参数对地震波场的影响

吴永祺，张海明

北京大学地球与空间科学学院地球物理系,北京 100871

0 引言

通过观测仪器记录的地面震动蕴含了有关地球介质和震源过程的信息，因此通过对比理论地震图与实际观测结果，可以了解地球内部结构和震源破裂过程.理论地震图的计算需要设定震源的运动情况.早期的研究大多考虑均匀破裂的平面断层模型，都做出了震源时间函数在断层上各点一致(Hartzell,1978;Bouchon,1980)的假设.但是这种简单的震源模型在很多情况下不能很好地描述震源的复杂性.例如实际的地震过程中，在断层面上的滑动分布是不均匀的，它们可能由复杂的断层几何形状、初始应力和摩擦系数等复杂性导致(Zhang et al.,2019).近二十年来，有很多基于复杂的震源模型的实际震例研究，例如1992年的Landers地震(Aochi and Fukuyama,2002;Wollherr et al.,2019)，2008年的汶川地震(Wen et al.,2012；Zhang et al.,2019)和2010年的海地地震(Douilly et al.,2015).基于符合物理规律的震源破裂过程计算得到理论地震图，并通过分析掌握波场的特征，是进一步进行反演获得发震区域的应力场等信息的基础.

地震波场与发震断层上的破裂过程密切相关，而影响断层破裂的因素之一是断层的几何复杂性.地震断层不同的几何形态，甚至平面断层上微小的几何扰动，都会导致不同的动态破裂过程，进而产生不同的地震波场(Madariaga,1983).断层的几何复杂性包括阶跃(袁杰和朱守彪，2014；Hu et al.,2016)，弯折(张丽芬等，2016)，分叉(Kame et al.,2003;Bhat et al.,2007)和断层面上的粗糙度(Shi and Day,2013;Luo and Duan,2018).多数破坏性的地震往往都发生在几何形态复杂的断层系统上，由于断层空间延展尺度较大，断层的几何形状会对破裂过程产生重要的影响(马瑾等，1996).例如2008年的汶川地震，Zhang等(2019)考虑了断层为平面断层和非平面断层的情形，非平面断层的破裂会造成映秀县和北川县附近有明显的地面运动，但平面断层的破裂对北川县附近没有明显的影响,汶川地震断层的几何复杂性极大地影响了震源的动态破裂和地震波场的分布.又例如1992年的Landers地震，该地震的一个特征是在几个断层之间的破裂转移，基于动力学破裂的相关研究都能很好的重现该特征，并且都能给出与观测结果拟合较好的地震波场结果(Aochi and Fukuyama,2002;Wollherr et al.,2019).

除了断层的几何形状以外，初始破裂区位置、滑动弱化位移和初始应力等动力学参数也是影响地震波场的重要因素.初始成核区的不同位置，会导致不同的破裂过程，进而激发不同的地震波场.对于弯折断层，在足够的距离以积累能量的情况下，当破裂到达拐角处后，破裂方向的变化会辐射出强烈的地震波(Zhang et al.,2017).改变断层上的滑动弱化位移大小，初始应力大小也会改变断层的破裂过程.当滑动弱化距离较小，初始应力较大的情况下，往往容易产生超剪切破裂.超剪切破裂是研究人员重点关注的课题之一，在超剪切破裂过程中，断层不同时刻辐射的剪切波互相干涉、叠加，形成马赫波，使得地震波振幅更大，辐射范围更广，往往造成更严重的地震灾害(Bernard and Baumont,2005;Dunham and Archuleta,2005;Dunham and Bhat,2008).超剪切地震的能量可以大幅度地传播到更远的地方，但是它在断层附近的地震动要比亚剪切地震引起的地震动要弱(Huang et al.,2018).

复杂断层系统的自发破裂过程模拟对计算方法提出较高的要求.目前常用的有两类方法.一类为域方法，包括有限差分法(Madariaga et al.,1998;Day et al.,2005;Zhang et al.,2006,2014)、有限元方法(Aagaard et al.,2001a,b;Oglesby et al.,2003;Barall,2009).域方法在计算过程中会同时获得破裂过程和地震波场.由于方法本身对于处理复杂断层的情况有技术困难，因此采用这两种方法研究三维的弯折和分叉断层的研究相对较少.另一类方法是半解析的边界积分方程方法(BIEM,Aochi et al.,2000;Chen and Zhang,2006;Zhang and Chen,2006a,b)，将问题归结到断层平面上，因此相比于域方法，在处理复杂几何断层问题时(如弯折、分叉)更为简便.

本文将基于三维空间非结构化的BIEM计算的自发破裂结果作为震源输入，利用分层介质中的广义反透射系数方法(Chen,1999)计算地震波场.针对弯折和分叉的情况，分别研究断层几何形状的改变、初始成核区位置的不同以及超剪切破裂对地震波场的影响，最后讨论介质模型对地震波场的影响.

1 研究方法

1.1 动力学破裂及位移场计算

本文通过BIEM计算断层上的自发破裂过程，断层应力与滑动速率的关系(Das and Aki,1977)为：

(x∈Γ)

(1)

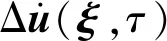
在断层自发破裂模拟的过程中，需要通过摩擦准则控制其破裂行为.而在同震破裂过程的模拟中，通常采用滑动弱化摩擦准则(Ida,1972)：

(2)

其中，τ是当前时刻单元的剪切应力值，τu和τf分别是破裂强度和残余应力，Dc为临界滑动弱化位移，D为当前时刻的单元累积滑动量.

本文以自发破裂的结果作为输入，运用广义反透射系数法(Chen,1999)计算每个单元的地震波场，通过点源叠加的方式计算整个断层系统的地震波场.当断层距离地表几公里以上时，地表的效应基本上可以忽略(Zhang and Chen,2006b)，全空间介质模型与半空间模型的破裂过程基本一致.因此，本文的数值模拟中自发破裂过程采用无限空间模型，而计算地震波场采用半空间和分层半空间模型.

1.2 正确性检验

Bouchon(1980)利用离散波数法计算了半空间走滑断层的位移场.本文与该结果进行比较，来验证计算方法的正确性.计算模型如图1所示，其中直立的断层长30 km，宽5 km，埋深2 km，断层破裂速度2.2 km·s-1，初始破裂位置在断层最左侧，从左向右均匀破裂.震源时间函数为斜坡函数，上升时间0.5 s.P波和S波波速分别为6.0 km·s-1和3.5 km·s-1，介质密度2.8×103kg·m-3.一共5条测线，在每条测线上各取10个观测台站，分别距离断层迹线0,1,2,3,4,6,8,10,15,20 km.计算得到的位移场结果如图2所示.通过比较可以发现，本文计算的结果和Bouchon的结果基本一致，在一定程度上验证了本文用于计算地震波场的方法的可靠性.

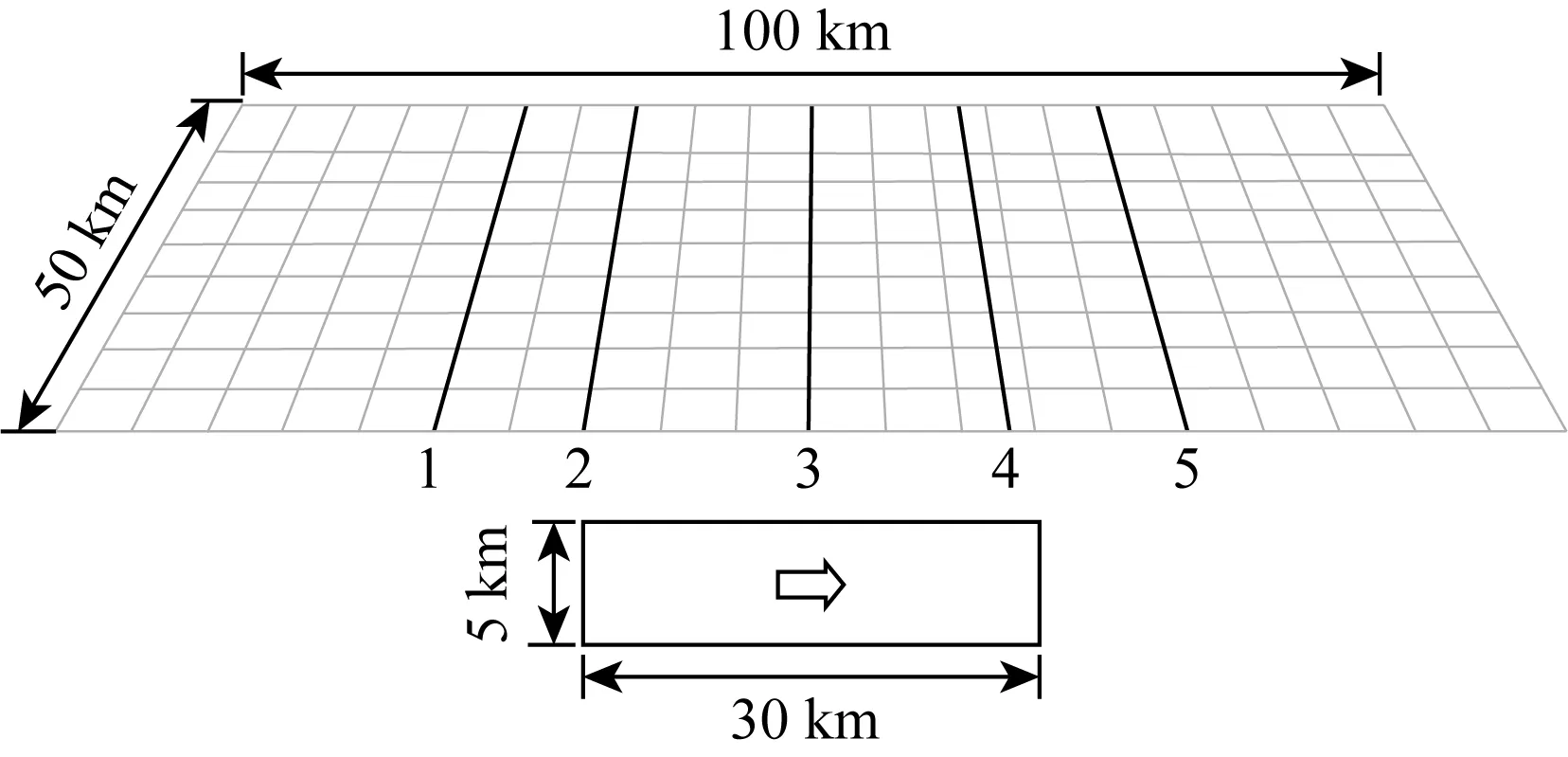
图1 Bouchon(1980)计算模型示意图粗线表示接收点所在观测线，观测线共5条，测线1距断层左侧10 km，测线2穿过断层左侧，测线3距断层左侧15 km，测线4距断层左侧28 km，测线5距断层左侧50 km.每条测线上分布10个台站，分别距离断层迹线0,1,2,3,4,6,8,10,15,20 km.Fig.1 Geometry of the model in Bouchon (1980)The bold line indicates the observation line where the receiving point is located.There are 5 observation lines.Lines 1 is 10 km away from the left side of the fault,line 2 passes through the left side of the fault,line 3 is 15 km from the left side of the fault,line 4 is 28 km from the left side of the fault,and line 5 is 50 km from the left side of the fault.There are 10 stations on each survey line,which are 0,1,2,3,4,6,8,10,15,20 km away from the fault trace.

2 数值结果及讨论

实际地震的几何形状非常复杂，如1992年兰德斯MW7.3地震，2016年凯库拉MW7.9地震.为了研究复杂的断层模型，可以将断层复杂的几何形态抽象不同几何模型的组合，如弯折、分叉、阶跃.这样便可以针对每一类几何模型，研究其如何影响地震波场.其中弯折断层是一种最为典型的断层几何结构，因此研究不同形态的弯折断层，可以进一步理解弯折断层会对地震波场产生何种影响.相较于弯折断层，分叉断层具有更加复杂的几何形态，其产生的地震波场也将具有更加复杂的特征，同时考虑到边界积分方法在处理复杂几何模型的优势，我们也将对分叉断层模型进行考察.因此，本文将基于弯折断层和分叉断层进行地震波场性质的研究.本文以下的数值计算，均采用相同的半空间介质模型，P波和S波波速分别为6.0 km·s-1和3.5 km·s-1，介质密度2.8×103kg·m-3.断层为走向90°的走滑断层.

2.1 弯折断层不同弯折角对地震波场的影响

对于弯折断层，不同的弯折角会影响破裂的传播和停止.通常，过大的弯折角将抑制破裂的传播，因此我们考察在其他动力学参数不变的情况下，弯折断层不同弯折角对于地表地震波场分布的影响.断层宽10 km，主平面长30 km，分支平面长15 km，如图3所示.考虑弯折角分别为0°、20°和30°的情况，初始破裂位置在距离主平面左侧20 km处.断层上破裂强度为60 MPa，成核区内初始应力为72 MPa，成核区外初始应力为48 MPa，静摩擦系数为0.6，动摩擦系数为0.1，成核区半径2.5 km.图4为不同弯折角的弯折断层的破裂速度快照，随着弯折角的增大，分支平面的破裂速度变小.图5和图6分别为地表峰值位移(PGD)分布和地表峰值速度(PGV)分布.如图所示，对于东西(EW)分量和竖直(UD)分量，当弯折角为0°时(即平面断层)，PGD和 PGV都关于断层对称分布；当断层弯折角增加为20°后，由于断层角度的改变，PGD和PGV最大值出现在弯折平面断层的走向方向(即东南方向)上，而东北方向上的地震波场减弱；当断层弯折角增加到30°后，由于弯折断层弯折角的增大会抑制破裂的传播，对应方向上地震波场会减弱，能观察到断层右侧地表地震波场明显被削弱.对于南北(NS)分量，当弯折角为0°时，如图5a2和图6a2 所示，地震波场的NS分量表现出明显的方向性效应，即在沿着破裂的方向上，垂直于主断层平面走向方向的地震波场分量表现出最大值.而随着弯折角的增大，由于弯折断层的阻碍效应，如图5c2和图6c2 所示，在断层右侧的地震波南北分量会被削弱.由于初始破裂位置位于主平面断层上，破裂向两侧传播，因此过初始破裂位置且垂直于主平面断层的位置，地震波场的PGD和PGV值最小.在固定其他计算参数的情况下，改变弯折平面断层的弯折角，会使得PGD(或PGV)的最大值沿着弯折方向移动；同时，由于弯折断层的阻碍效应，当弯折角过大时，会对该方向上的地震波场起到抑制作用(张丽芬等，2016).

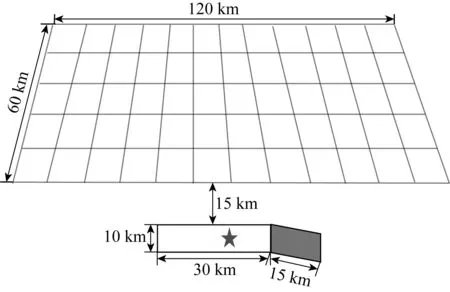
图3 弯折断层模型断层宽10 km，主平面(白色)长30 km，弯折平面(灰色)长15 km，断层上沿距地表15 km.五角星表示初始破裂位置，距断层左侧20 km.Fig.3 Geometry of the bending faultThe width of the fault is 10 km,the length of main plane (white)is 30 km,and the length of bend plane (gray)is 15 km,the upper edge of the fault is 15 km from the surface.The star represents the initial rupture position and is 20 km from the left side of the fault.

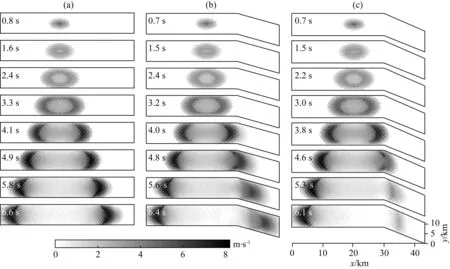
图4 不同弯折角的弯折断层滑动速率快照每个子图左侧数字表示断层破裂的不同时刻.(a)弯折角0°;(b)弯折角20°;(c)弯折角30°.Fig.4 Snapshots of the slip rate of bending faults with different bending anglesThe numbers on the left indicate different moment in the fault rupture process.(a)Bending angle 0°;(b)Bending angle 20°;(c)Bending angle 30°.

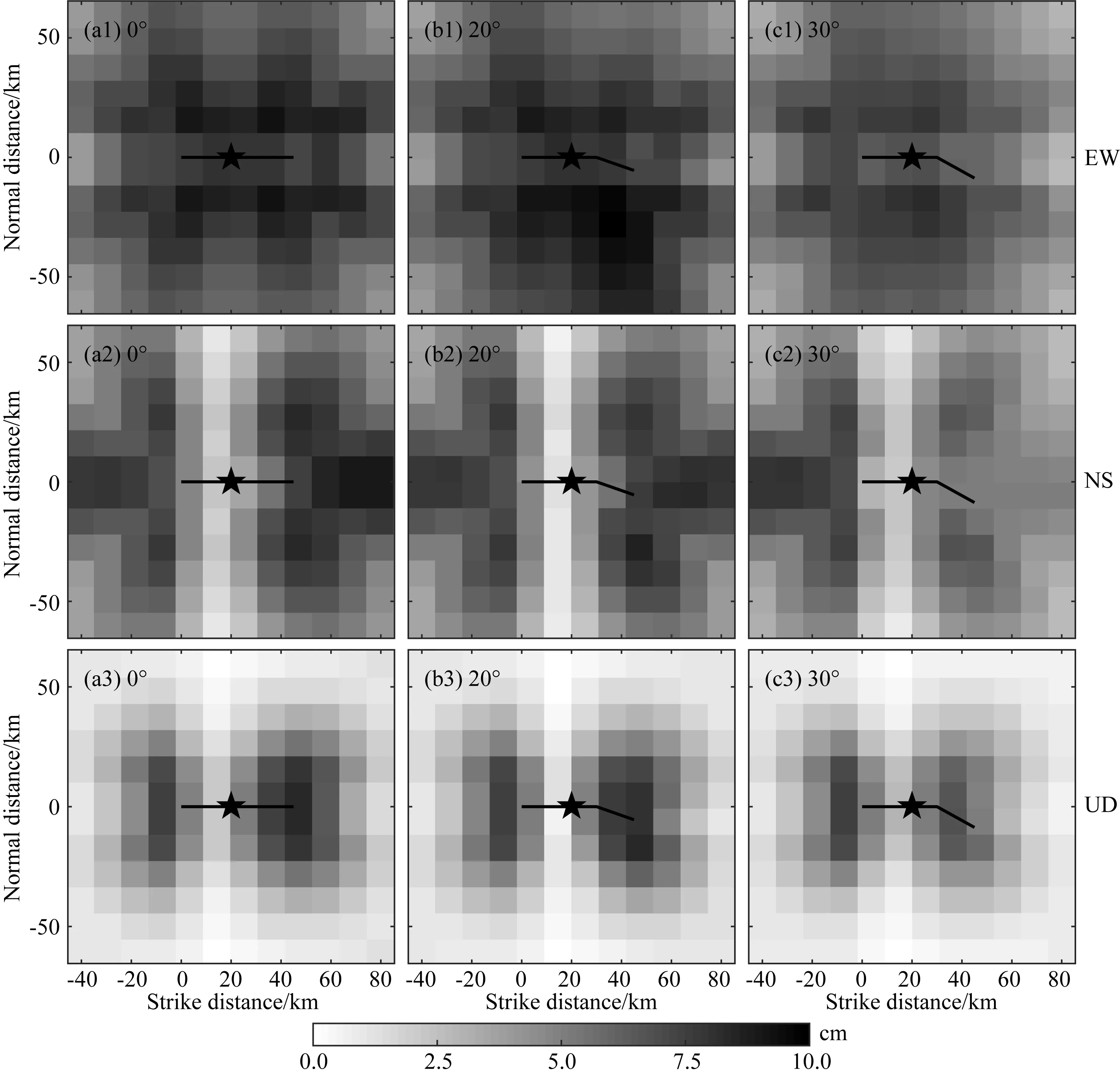
图5 不同弯折角的弯折断层引起的地表峰值位移场(PGD)分布图从上到下分别为东西(EW)分量，南北(NS)分量和竖直(UD)分量的PGD分布图.五角星为初始破裂位置，黑色实线为断层在地表投影.(a)弯折角0°;(b)弯折角20°;(c)弯折角30°.Fig.5 Distribution map of the peak ground displacement (PGD)caused by bending faults with different bending anglesFrom top to bottom are the PGD distribution diagrams of the east-west (EW)component,the north-south (NS)component and the vertical (UD)component.The star is the initial rupture position,and the solid black line is the projection of the fault on the surface.(a)Bending angle 0°;(b)Bending angle 20°;(c)Bending angle 30°.

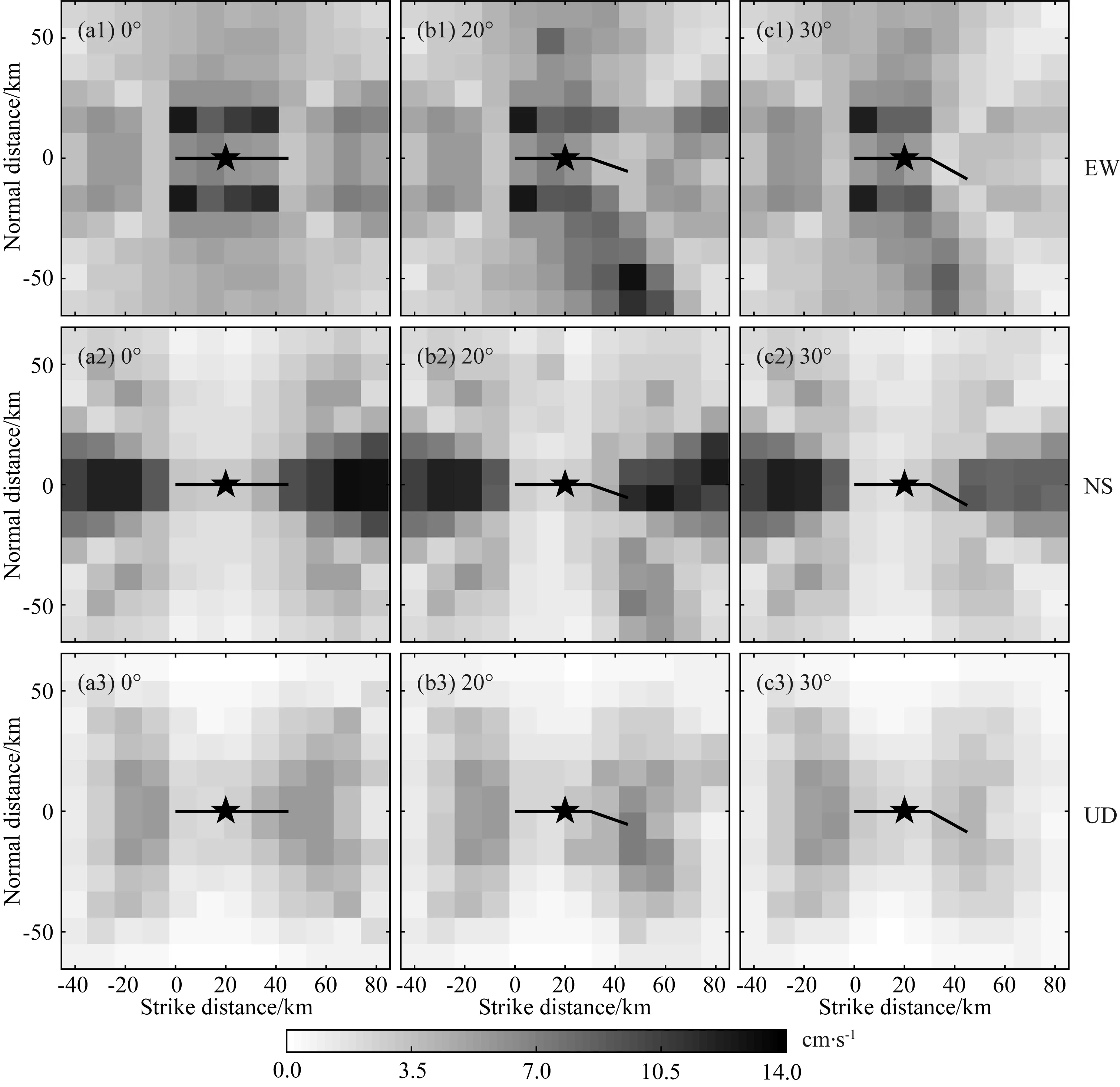
图6 不同弯折角的弯折断层引起的地表峰值速度(PGV)分布图(a)弯折角0°;(b)弯折角20°;(c)弯折角30°.其余图例说明同图5.Fig.6 Distribution of peak ground velocity (PGV)caused by bending faults with different bending angles(a)Bending angle 0°;(b)Bending angle 20°;(c)Bending angle 30°.The rest of the illustrations are the same as Fig.5.

2.2 不同成核区位置对地震波场的影响

在同一种几何模型下，其他动力学参数相同，成核区位置的不同也会造成不同的破裂过程，进而导致不同的地震波场.因此，需要考虑不同成核区位置对地震波场的影响.计算模型参考图3，断层为弯折角30°的弯折断层，主断层长30 km，分支断层长15 km.选取成核区位置位于距离主断层左侧5 km，10 km和15 km处.图7和图8分别为计算得到的PGD和PGV三分量结果.可以看到，无论是PGD还是PGV，成核区距断层左侧距离从5 km到15 km变化时，破裂从以从左向右破裂为主变化为双侧破裂，地震波场峰值分布也呈类似的变化.当初始破裂位置在断层左侧时，对地表地震波场的影响主要集中在右侧，同时，在地震波场的南北分量上表现出明显的方向性效应，即沿着断层破裂方向上地震波场峰值最大，而逆破裂方向上地震波场峰值最小.随着初始破裂位置的右移，断层左侧的地震波场逐渐变大，在断层两侧的地表都会出现较大的破坏.值得注意的是，当初始破裂区距离弯折断层的弯折处最远，如图7a 和图8a 所示，断层破裂在沿破裂方向上产生的地震波场造成的破坏也最大，这是因为距离越远，破裂具有更大的能量，断层将在地表产生更大的地震波场 (Xu et al.,2019).因此，在其他参数相同的情况下，对于弯折断层，不同成核区位置的地震，会对地表造成截然不同的破坏，当破裂在断层上的破裂距离越长，破裂具有更大的能量，地震在地表造成的破坏也越大.

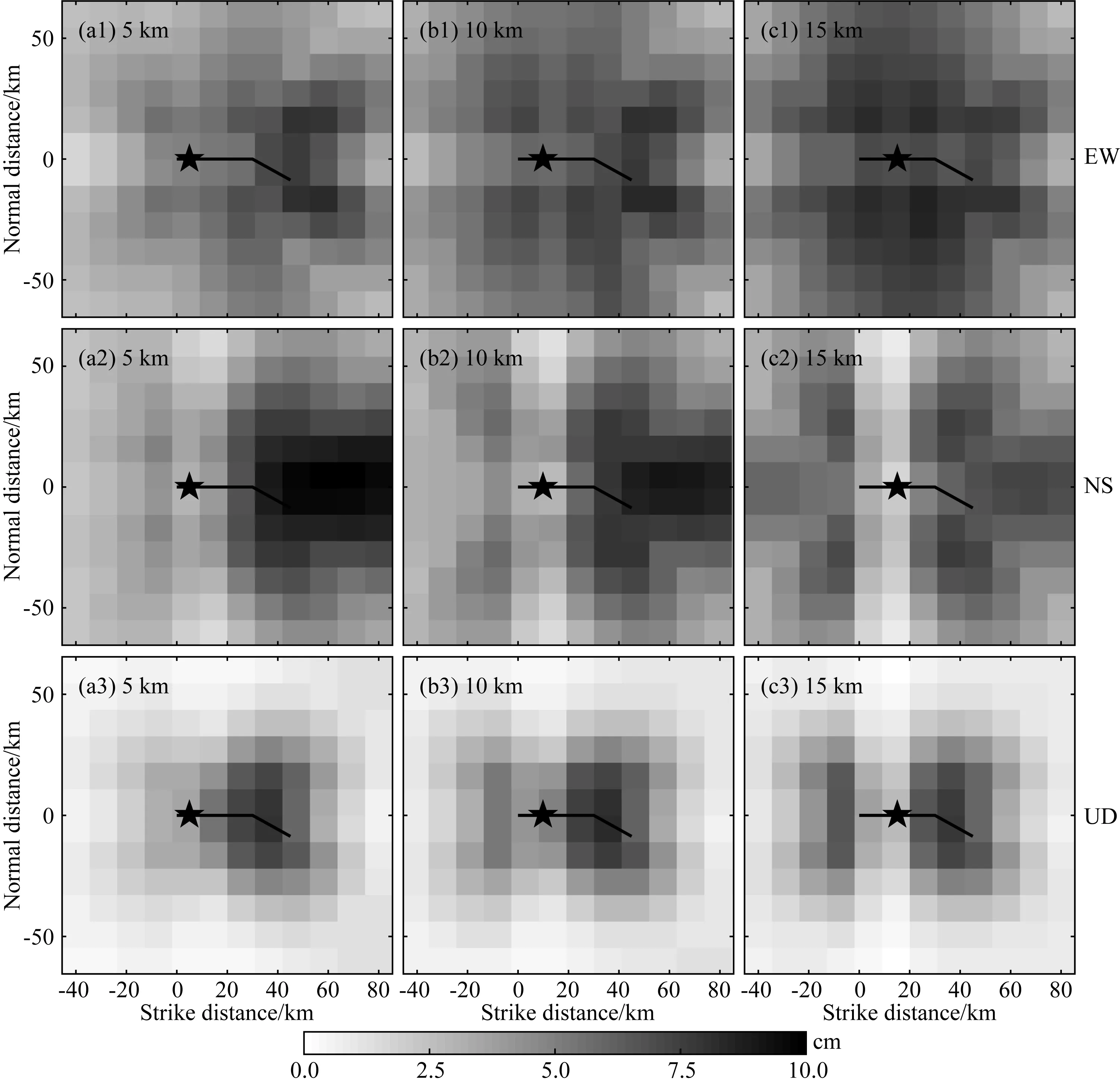
图7 弯折断层不同初始成核区位置地表峰值位移场(PGD)分布图(a)初始破裂位置距断层左侧5 km;(b)初始破裂位置距断层左侧10 km;(c)初始破裂位置距断层左侧15 km.其他图例说明同图5.Fig.7 Distribution of peak ground displacement (PGD)at different initial nucleation areas of bending faults(a)The initial rupture location is 5 km away the left side of the fault;(b)The initial rupture location is 10 km from the left side of the fault;(c)The initial rupture location is 15 km from the left side of the fault.Other legends are the same as Fig.5.

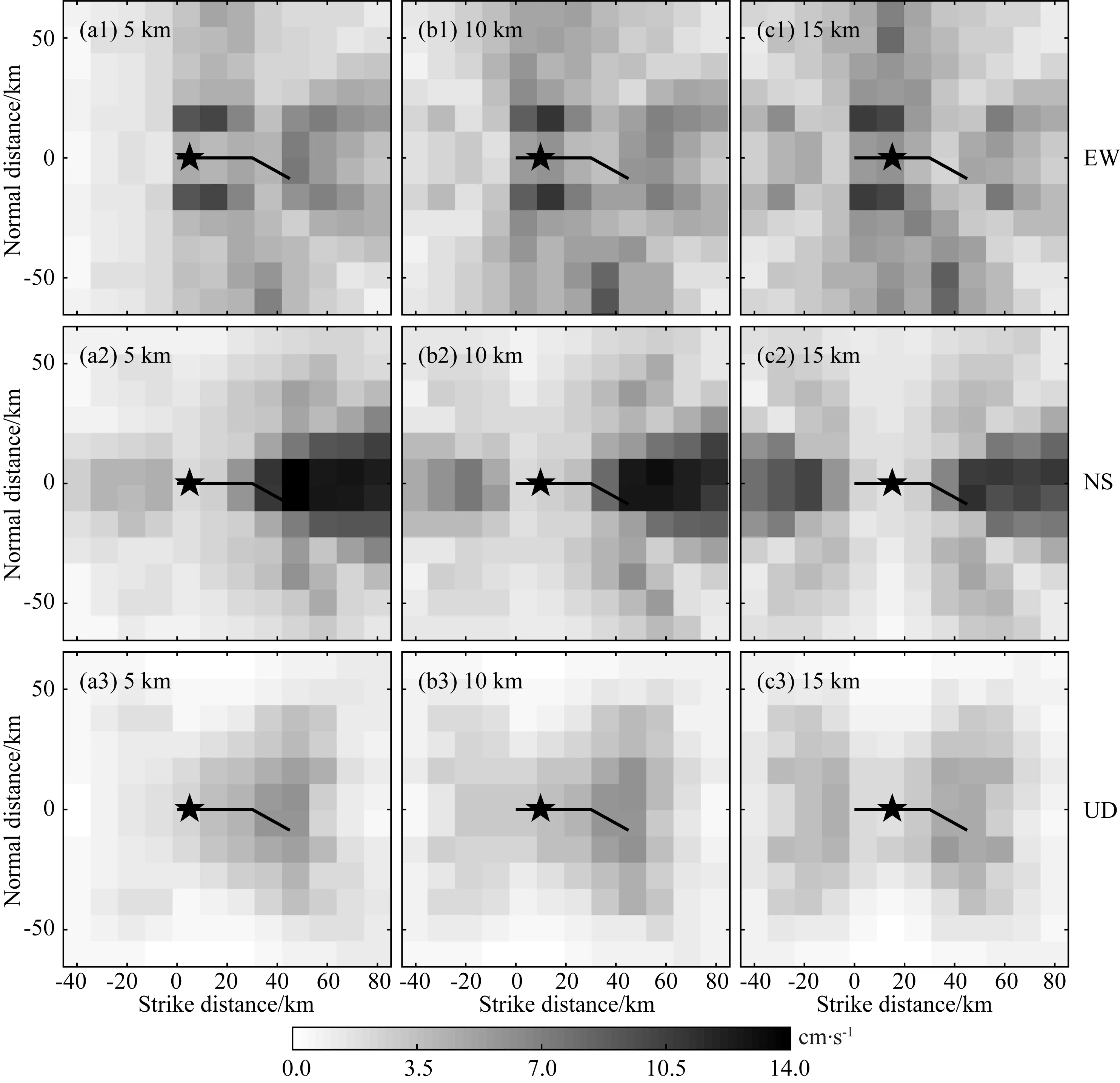
图8 弯折断层不同初始成核区位置地表峰值速度(PGV)分布图(a)初始破裂位置距断层左侧5 km;(b)初始破裂位置距断层左侧10 km;(c)初始破裂位置距断层左侧15 km.其他图例说明同图5.Fig.8 Distribution of peak ground velocity (PGV)at different initial nucleation areas of bending faults(a)The initial rupture location is 5 km away the left side of the fault;(b)The initial rupture location is 10 km from the left side of the fault;(c)The initial rupture location is 15 km from the left side of the fault.Other legends are the same as Fig.5.

2.3 超剪切对地震波场的影响

在同一种几何模型下，其他动力学参数相同，改变初始应力大小或者滑动弱化距离会得到不同的破裂过程，其中，当初始应力较大或者滑动弱化距离较小的情况下可能产生超剪切现象，而断层上超剪切破裂的发生往往会导致地表严重的破坏.因此，我们需要重点关注超剪切破裂对地表位移场的影响.我们使用无量纲化公式(Xu et al.,2015；郑玲珑等，2021)模拟平面断层的动态破裂过程:

(3)

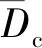
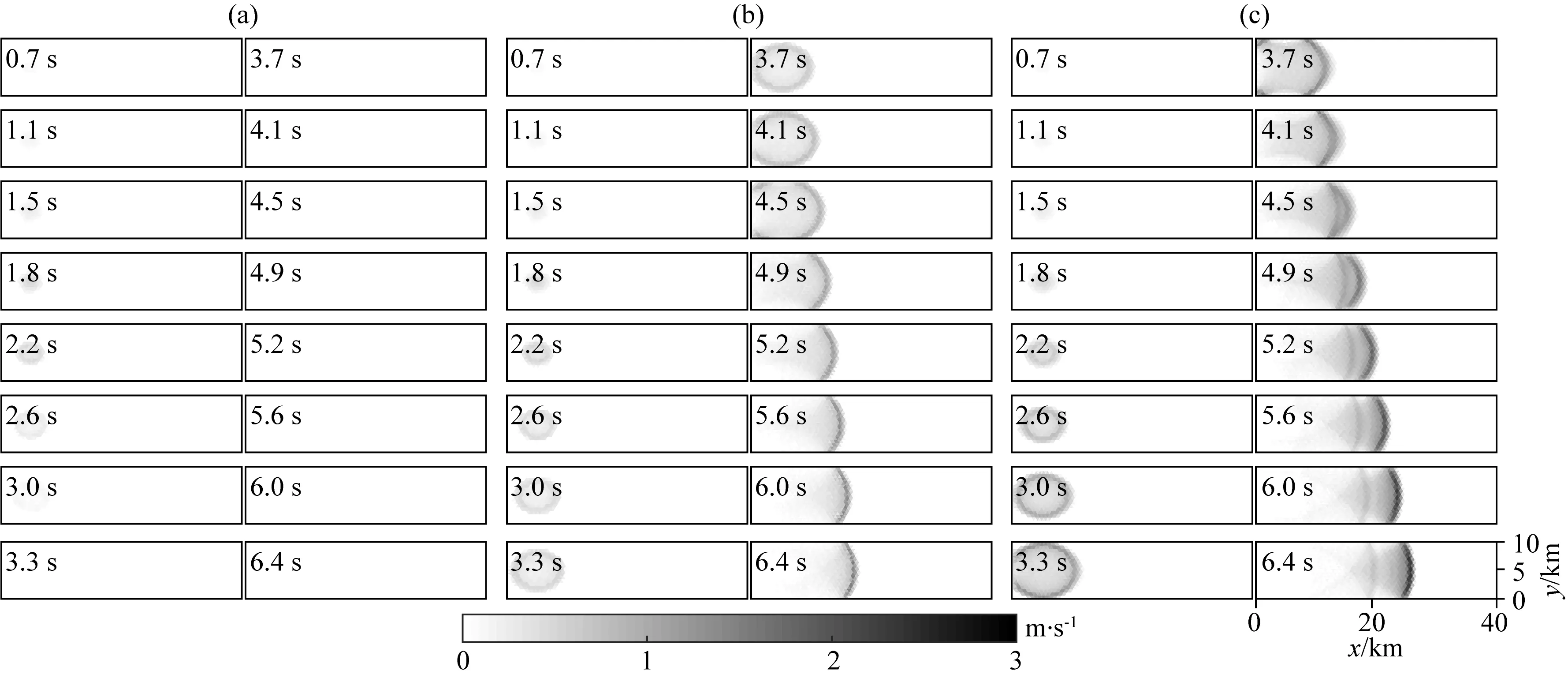
图9 平面断层自发破裂滑动速率快照每个子图左侧数字表示断层破裂的不同时刻.(a)模型S1破裂自发停止；(b)模型S2亚剪切破裂；(c)模型S3超剪切破裂.Fig.9 Snapshot of the spontaneous rupture slip rate on the plane faultThe numbers on the left indicate different moment in the fault rupture process.(a)Model S1;(b)Model S2 with subshear rupture;(c)Model S3 with supershear rupture.

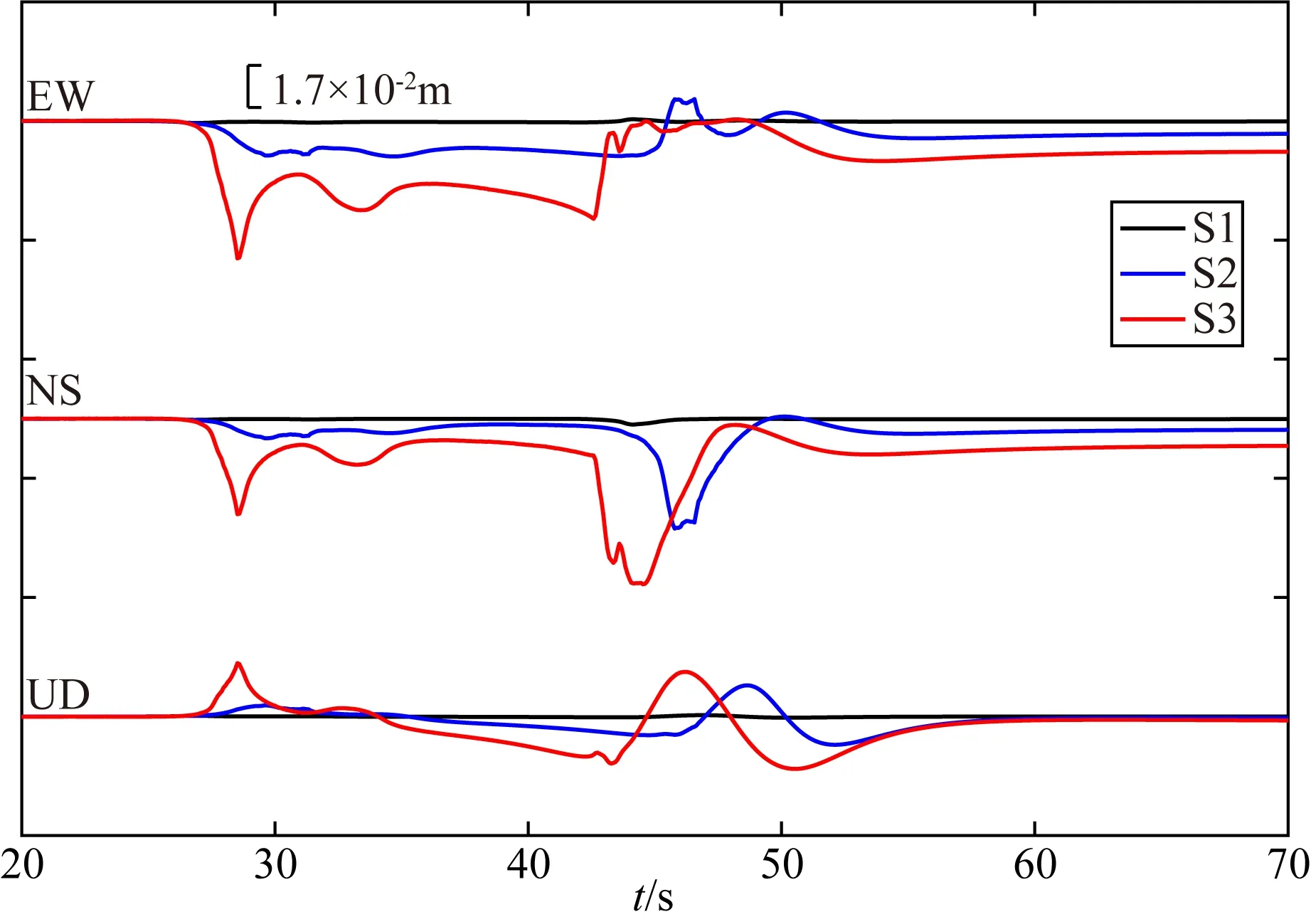
图10 平面断层地表位移场从上到下分别为东西(EW)分量，南北(NS)分量和竖直(UD)分量.黑线、蓝线和红线分别表示断层模型S1，S2和S3的位移场三分量.Fig.10 Surface displacement field of the plane faultFrom top to bottom are the east-west (EW)component,the north-south (NS)component and the vertical (UD)component.The black line,blue line and red line represent three components of displacements of the fault models S1,S2 and S3,respectively.

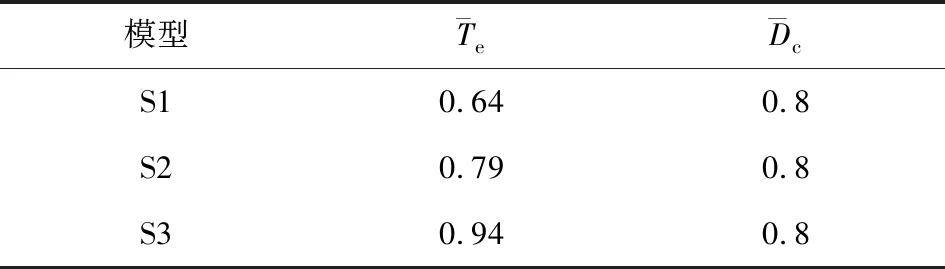
表1 不同初始应力平面断层模型Table 1 Plane fault models with different initial stresses

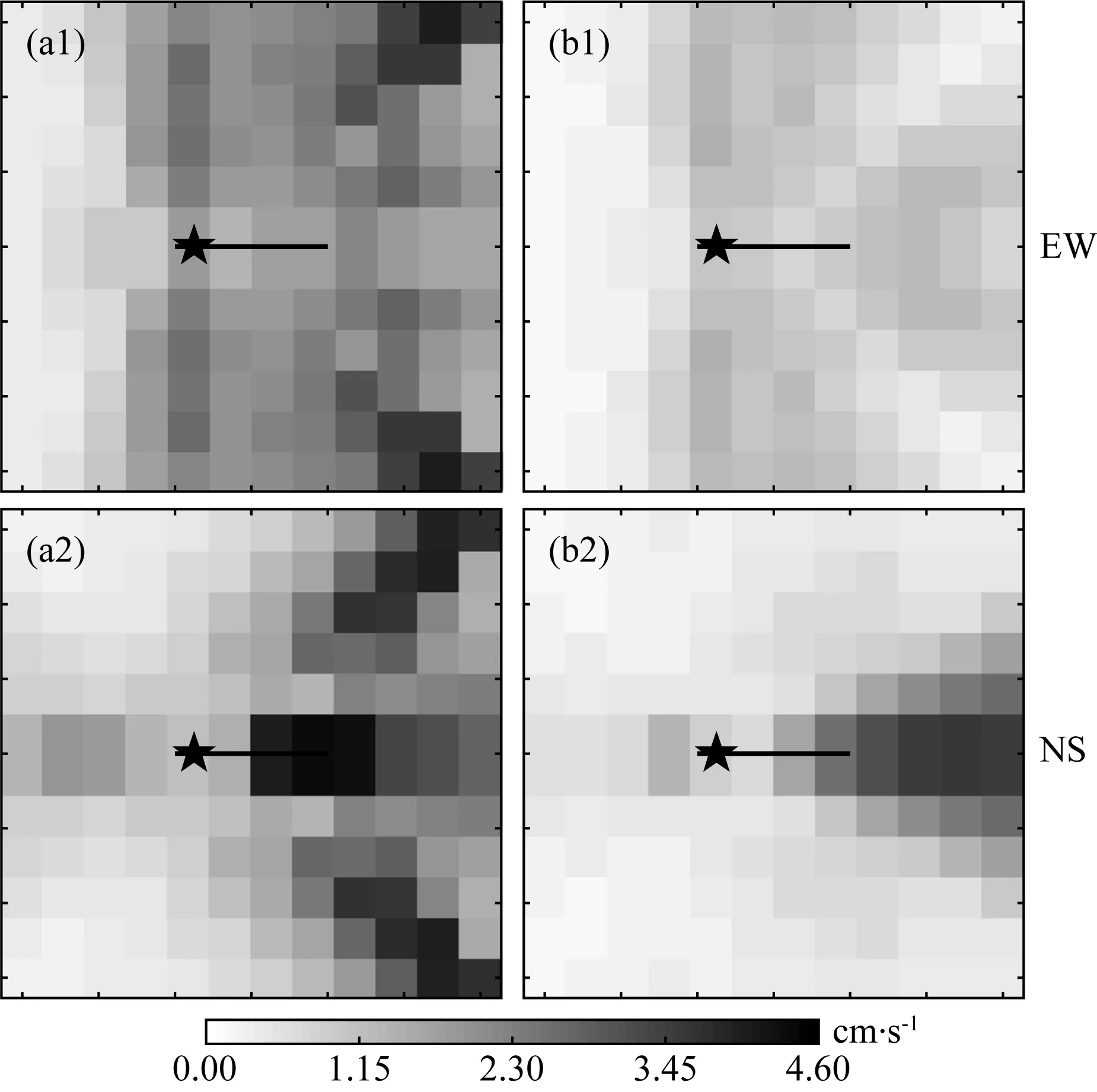
图11 平面断层地表峰值速度(PGV)分布从上到下分别为东西(EW)分量，南北(NS)分量.(a)发生超剪切破裂的模型S3 地表PGV分布;(b)发生亚剪切破裂的模型S2 地表PGV分布.其他图例说明同图5.Fig.11 Distribution of peak ground velocity (PGV)of the plane fault From top to bottom are the east-west (EW)component,the north-south (NS)component.(a)Model S3 PGV with supershear rupture;(b)Model S2 PGV with subshear rupture.Other legends are the same as Fig.5.

2.4 30°夹角的分叉断层

考察夹角为30°的不同形状的分叉断层对位移场的影响.如图12所示，主断层长30 km，两个分支断层长20 km.断层模型B1,B2,B3,B4各分支的张角(即与主平面的夹角，逆时针为正)由表2给出.动力学参数如2.1节所述.图13显示了各个模型中过断层中心线上的位置处的滑动速率随时间的变化.可以观察到模型B1和模型B2分叉面A破裂占优，而模型B3和模型B4分叉面B破裂占优.随着分叉面A角度越来越大，破裂从分叉面A逐渐转移到分叉面B.同时，无论是在哪个分叉面破裂，优势分支的角度越小，滑动速率越大.计算的地表位移场如图14所示，地表位移场的波形特征与断层破裂结果有着明确的对应关系.在接收点a，位移场结果如图14a 所示，由于模型B1和模型B2的破裂时间更长，因此，能观测到更长的波形.同时对于模型B4，由于其在断层分支上的破裂速度最大，破裂最强烈，故该断层对应的位移场峰值在几个模型中也是最大的.在接收点b的位移场如图14b所示，能看到在南北和竖直分量上，几个断层模型计算得到的位移场十分接近.这是由于将接收点沿着南北方向做投影，投影点会落在断层的两个分支上，考虑上文所提到的方向性效应，因此分叉断层的两个分支平面在南北分量和竖直分量的位移场值贡献很小，位移场主要由相同的主平面主导，几个模型得到位移结果相近.增大震中距，让观测点的投影落在断层外，不同断层模型的位移场差别将变大，结果如图14c 所示.

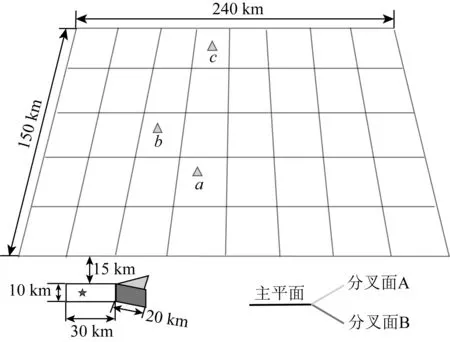
图12 分叉断层模型断层宽10 km，主平面长30 km，两个分支平面长20 km，断层上沿距地表15 km.五角星表示初始破裂位置，三角形表示接收点.接收点a震中距71 km，方位角56.0°；接收点b震中距75 km，方位角25.5°；接收点c震中距145 km，方位角26.7°.Fig.12 Branching fault modelThe width of the fault is 10 km,the length of main plane is 30 km,and the length of two branching planes is 20 km.The upper edge of the fault is 15 km from the surface.The star represents the initial rupture position.The triangle represents the receiver.The epicenter distance of receiver a is 71 km and the azimuth is 56.0°;the epicenter distance of receiver b is 75 km and the azimuth is 25.5°;the epicenter distance of receiver c is 145 km and the azimuth is 26.7°.

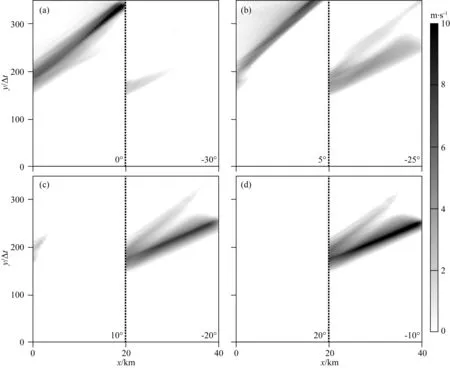
图13 分叉断层分支滑动速率时空分布图虚线左侧为分叉面A，右侧为分叉面B.(a)模型B1；(b)模型B2；(c)模型B3；(d)模型B4.Fig.13 Space-time diagrams of the slip rate along the branch planes of the branching faultsThe left side of the dashed line is surface A,and the right side is surface B.(a)Model B1;(b)Model B2;(c)Model B3;(d)Model B4.

表2 不同分叉断层模型Table 2 Different branching fault models

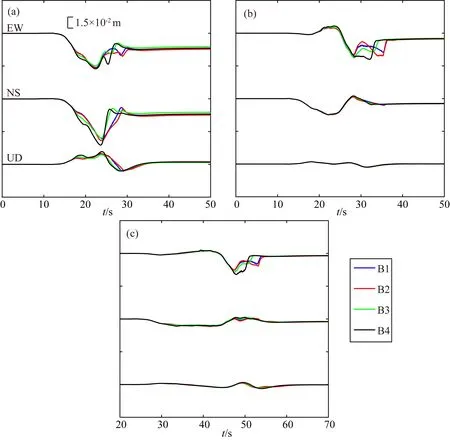
图14 不同的分叉断层模型上自发破裂导致的地表位移随时间的变化每个子图中从上到下分别为东西(EW)分量，南北(NS)分量和竖直(UD)分量.B1，B2，B3，B4为四个断层模型.(a)接收点a计算结果；(b)接收点b计算结果；(c)接收点c计算结果.Fig.14 Displacement caused by spontaneous rupture on different branching faultsFrom top to bottom are the east-west (EW)component,the north-south (NS)component and the vertical (UD)component in the subplot.B1,B2,B3 and B4 are four fault models.(a)The result of receiver a;(b)The result of receiver b;(c)The result of receiver c.

3 讨论与结论

除了上述各种因素以外，介质模型也是一个可能影响地表位移场的因素.考虑如表3、表4、表5所示的介质模型半空间模型L1，两层介质模型L2，含低速层的三层介质模型L3.考虑如上文所示弯折角20° 的弯折断层，断层深度15 km.位移场计算结果如图15所示.相较于其他介质模型，由于低速层速度更小，L3模型对应各震相到达更迟.同时，由于低速层对位移场的放大效应，能观察到L3模型下的位移场振幅更大.

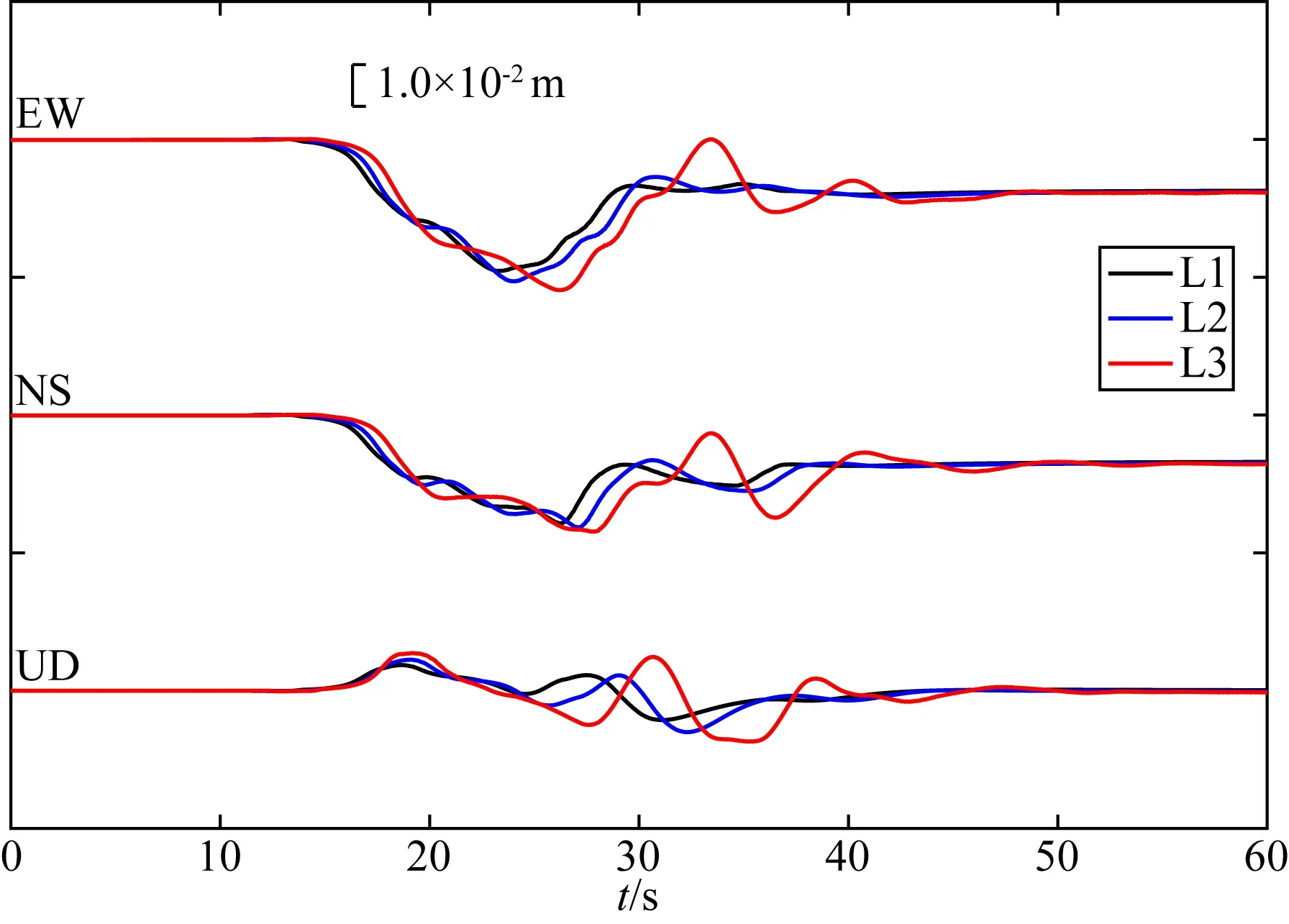
图15 不同介质模型下的位移场从上到下分别为东西(EW)分量，南北(NS)分量和竖直(UD)分量.蓝线、红线和绿线分别表示半空间介质模型L1，两层介质模型L2和含低速层的三层介质模型L3.Fig.15 Displacement field under different media modelsFrom top to bottom are the east-west (EW)component,the north-south (NS)component and the vertical (UD)component.The black line,the blue line and the red line represent the half-space medium model L1,the two-layer medium model L2,and the three-layer medium model L3 with low velocity layers,respectively.

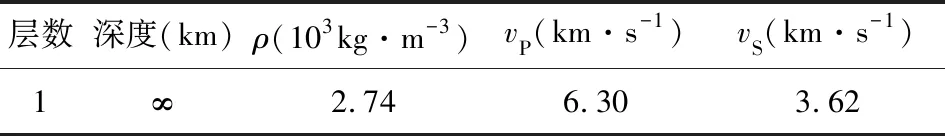
表3 半空间介质模型L1Table 3 Half-space medium model L1

表4 两层介质模型L2Table 4 Two-layer medium model L2

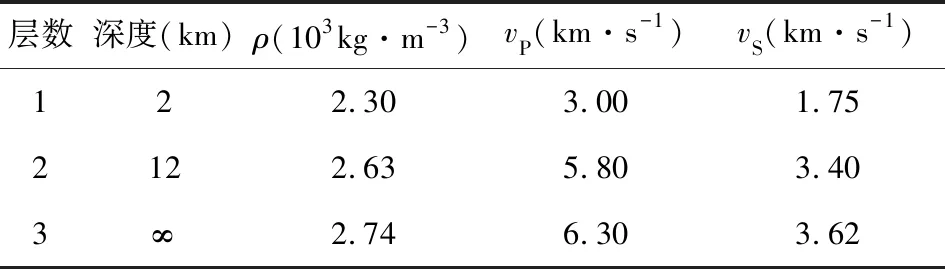
表5 含低速层的三层介质模型L3Table 5 Three-layer medium model with low-velocity layer L3

本文基于BIEM模拟了断层的自发破裂过程，并根据此结果计算断层对应的地震波场.讨论了不同断层几何形状，成核区位置、超剪切破裂以及介质模型分别对地震波场的影响，得到如下结论：

(1)动力学参数不变，对于不同弯折角的弯折断层，弯折角度变化能明显改变地表地震波场的分布.对于小弯折角的情形，沿弯折分支走向的方向上地震波场具有最大值；但是，对于大弯折角的情形，由于弯折断层的抑制效应，会使得沿弯折断层走向方向上的地震波场都较小.

(2)对于弯折断层，其他动力学参数不变，改变初始成核区的位置，当破裂在断层上的传播距离越长，破裂的能量越大，地震在地表造成的破坏越大.

(3)对于弯折断层，其他动力学参数不变，增大断层面上的初始应力，能增大断层上破裂的滑动速率，当初始应力足够大时，断层上会产生超剪切破裂，而超剪切的破裂的产生会明显增大地震波场的振幅，激发高频成分，使得部分震相到时提前，并增大永久位移，同时，超剪切破裂产生的地震波场在空间中的衰减更为缓慢，从一定程度上能解释为什么发生超剪切的地震会造成更大的破坏.

(4)对于分叉断层，在断层上破裂时间越长，对应的地震波场具有更宽的波形；断层上破裂强度越大，对应的地震波场的峰值也越大.

(5)低速层会增大地表波场的振幅，同时会使得波形上各震相到达时间更迟.

本文探讨了断层动力学自发破裂过程与其产生的地震波场的联系，计算了不同几何形态和不同动力学参数下自发破裂断层引起的地震波场，可以由此评估不同断层破裂对地表造成的破坏情况.实际地震具有更高的复杂性，包括更复杂的断层几何特征、更复杂的动力学参数、更复杂的介质信息，因此，有必要更加细致的考察断层的各种复杂性是如何影响地震波场的特征，为下一步的动力学参数反演提供基础.同时将模拟的地震波场分布与实际的地震破坏比较，以便于为未来的灾害评估提供参考意见.这些是进一步的研究中予以考虑的重要内容.