地球外部扰动重力严密改化模型及分析检验

黄谟涛，邓凯亮，吴太旗，欧阳永忠，陈欣，熊雄，刘敏，王许

1 海军研究院，天津 300061 2 自然资源部海洋环境探测技术与应用重点实验室，广州 510300 3 91001部队，北京 100830

0 引言

外部扰动重力计算是地球重力场逼近建模研究内容的重要组成部分，也是解算大地测量边值问题的主要应用目标之一.外部扰动重力信息在航空航天器飞行轨迹精密计算和空间科学技术研究中具有重要的应用价值(Hirvonen and Moritz,1963；Moritz,1966；Heiskanen and Moritz,1967；Cruz and Laskowski,1984；黄谟涛等,2005).除代表中长波长的全球重力场球谐展开位模型外，常用于计算地球外部扰动重力三分量的解析函数模型还包括直接积分和等效源两大类别，前者包含Stokes积分模型、表层积分模型和向上延拓积分模型(Heiskanen and Moritz,1967；刘长弘,2016)；后者包含等效重力异常模型(Bjerhammar,1964；李建成等,2003)、质点模型(Sünkel,1983；吴晓平,1984；黄金水和朱灼文,1995；黄谟涛等,2005；王建强等,2010)和虚拟单层密度模型(许厚泽等,1984；操华胜等,1985).计算模型的完备性及决定其计算效率高低的模型结构复杂程度，是评价模型优劣和实用性的两个关键因素.黄谟涛等(2018,2019)已对前述不同类别计算模型的技术特点和适用条件做了分析比较和总结，为不同应用领域选用合适的计算模型提供了理论参考依据.

早在1986年，许厚泽等就曾针对利用直接积分法计算高空扰动重力的模型改化和精度评估问题做过深入研究(许厚泽等，2014).但精密计算外部扰动重力的难点主要集中在接近地球表面的超低空高度段，具体体现为地形效应和积分奇异性两个方面的干扰.通过联合采用Stokes球面积分模型和Molodensky级数改正项(Heiskanen and Moritz,1967)、Bjerhammar等效重力异常(Bjerhammar,1964)、Moritz解析延拓改正项(Moritz,1980)等方法，均可有效补偿低空地形效应对计算参量的影响；针对积分奇异性干扰，黄谟涛等(2005)推出了基于环带扇形数据分布的非奇异积分公式.根据实用化保障需求，黄谟涛等(2018)提出了基于插值替换的非奇异分段积分改进公式.尽管上述两组公式都成功避开了积分奇异性问题，但前者对输入数据分布有特殊要求，其应用范围受到了较大限制；后者的计算精度取决于插值高度和插值模型的选择及计算区域重力异常场变化的剧烈程度，具有一定的不确定性.针对海域应用需求，黄谟涛等(2019)推出了以重力异常和高程异常作为输入信息、基于表层积分模型的无奇异计算公式，解决了海域外部近地空间流动点扰动重力精密快速赋值问题.实际上，该研究思路同样适用于解决以单一重力异常作为输入信息的Stokes球面积分模型改化问题.综合考虑计算模型选择的灵活性需求和数据保障种类可能面临的局限性制约，本文沿用黄谟涛等(2019)的研究思路，通过引入基于积分恒等式变换的移去恢复技术及平面局域泰勒级数展开方法，对计算外部扰动重力三分量的Stokes全球积分模型进行分步改化处理，旨在消除数值积分不连续性和积分核函数奇异性的影响，提高赋值模型在超低空高度段的计算精准度.

1 地球外部扰动重力全球积分模型

由地球重力场位理论得知，扰动重力可由扰动位求偏微分得到，地球外部扰动位的全球积分公式为(Heiskanen and Moritz,1967)：

(1)

(2)

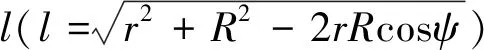
由式(1)可推得地球外部扰动重力三分量计算式：

(3)

(4)

(5)

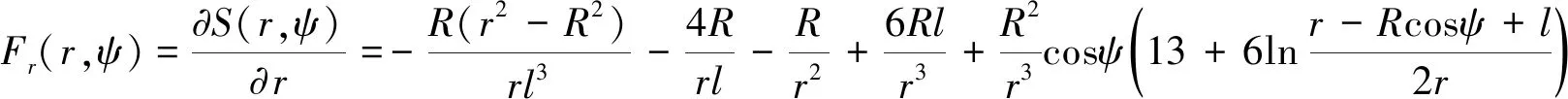
(6)

(7)

(8)

(9)

(10)

式(3)—(5)即为计算地球外部扰动重力矢量的全球积分模型.利用该组公式计算扰动重力三分量的精度主要取决于模型改化误差、输入数据分辨率及观测噪声等几个方面的因素(Heiskanen and Moritz,1967；黄谟涛等,2005).关于数据质量影响和数据需求分析方面的内容，黄谟涛等(2019)已经做了比较详细的研究和讨论，这里不再重复.本文主要针对式(3)—(5)实现过程可能引入的模型改化误差进行分析和探讨，并提出相应的补偿方法.

2 计算模型分析与改化

2.1 径向分量积分模型分析与改化

2.1.1 积分模型稳定性分析

由式(6)得知，当计算点趋近于数据网格点时，即当r→R和ψ→0时，会出现分母项l→0，积分核函数Fr(r,ψ)发生奇异.这说明利用式(3)计算超低空外部扰动重力径向分量时，会出现由核函数奇异引起的不确定性问题，无法保证计算结果的可靠性和有效性.尽管通过从积分域中直接扣除计算点所在的网格数据块，理论上即可消除积分奇异性问题，但因该数据块距离计算点最近，对计算结果的影响也就最大，故扣除该数据块必然会对计算结果带来一定程度甚至是不可忽略的影响，降低计算结果的精度(刘长弘,2016).另一方面，可以证明，当r→R和ψ→0时，由式(3)确定的外部扰动重力径向分量δgr并不严格收敛于球面上的理论预估值δgR，不符合数值逼近理论最基本的连续性要求(黄谟涛等,2019).具体证明如下.

根据Heiskanen和Moritz(1967)，由式(3)定义的地球外部扰动重力径向分量δgr可转换为如下的外部扰动位和重力异常的线性组合：

(11)

式中，扰动位Tr由式(1)确定；外部重力异常Δgr计算表达式为：

(12)

=Kr1(r,ψ)+Kr2(r,ψ),(13)

(14)

(15)

此时，式(11)可改写为三个积分和：

(16)

下面分别推证，当r→R时，上述三个积分项的逼近结果.首先，依据式(1)和式(2)，不难推得：

(17)

(18)

式中，S(ψ)为传统的球面Stokes函数.其次，依据式(14)和式(16)，可得：

(19)

考虑到当r→R和ψ→0时，式(19)中的积分核函数可能出现分子分母同时为零的不定式(0/0)情形，故需要对其做特殊处理.把式(19)的全球积分域σ划分为σ1和σ2两部分，σ1代表以计算点为中心、s1为半径且无限接近于计算点的小球冠区域，σ2代表剩余部分(σ-σ1)的区域.因当r→R时，Kr1(r,ψ)→0，对应于σ2部分的积分项为零，故我们只需要对小球冠σ1部分的积分进行讨论.在很小的σ1区块内，可采用极坐标系(s,α)，对由式(14)表示的积分核函数做平面近似处理，取：

r=R+h,R2dσ≈sdsdα,

式中，h代表计算点的大地高.此时，由式(14)表示的积分核函数可近似表示为：

(20)

将式(20)代入式(19)，得小球冠σ1部分也就是δgr1的积分为：

(21)

考虑到σ1是一个无限小的包围计算点的球冠，可将Δg看作恒等于球面计算点处的重力异常ΔgR的不变量，即认为Δg=ΔgR.将其代入式(21)，完成积分后得：

(22)

由式(22)不难看出，当h→0(即r→R)时，有：

δgr1(r→R)=-ΔgR.

(23)

(23)式说明，由式(19)定义的第二项积分极限值收敛于地面上已知重力异常的负值.

最后，依据式(15)和式(16)，我们不难得到式(16)右端第三项积分的极限值为：

(24)

因式(15)代表的是重力异常Poisson积分核函数的零阶和一阶项，故只有重力异常的零阶和一阶项为零这样的条件得到满足时，积分式(24)的极限值才为零.

综合式(17)、(23)和(24)，可得到式(16)的积分极限值为：

(25)

由式(24)和(25)得知，当r→R时，δgr(r→R)的极限值并未严格收敛于球面上的理论预估值：δgR=-2TR/R-ΔgR，除非满足假设条件：重力异常不包含零阶和一阶项.

实际上，式(25)的右端之所以会出现多余的第三项，是因为我们在对式(13)右端表达式做改化处理时，人为实施了“恢复-移去”两步运算，即首先在式(14)中恢复零阶和一阶项影响，然后在式(15)中移去相对应的影响项.而由Heiskanen和Moritz(1967)得知，人们在推导地球外部引力位球谐函数及其径向导数积分计算式时，总是习惯于事先自动“压制”掉计算参量的零阶和一阶球谐函数项，使得它们只适用于这样的参考椭球：①它与大地水准面具有相同的重力位；②它的质量与地球质量相等；③它的中心位于地球质心.显然，一般参考椭球不可能完全满足这些条件，因此，恢复积分核函数的零阶和一阶项，使原积分式成为适用范围更广的广义积分式才是合情合理的.正如Heiskanen和Moritz(1967)所述：“传统Stokes公式给出的扰动位Ts一般不包含零阶项T0和一阶项T1，将Ts加上T0和T1才能得到完整的扰动位T”.依据这样的思路，Pizzetti和Heiskanen曾分别推出了更为通用的Stokes积分公式(Heiskanen and Moritz,1967).

基于上述考虑，我们认为，在前面的改化处理时，只需要对式(13)做第一步的恢复处理，不必做第二步的移去运算.也就是说，只需考虑式(13)右端的Kr1(r,ψ)作用，不必顾及第二项Kr2(r,ψ)的影响.此时，Kr(r,ψ)=Kr1(r,ψ)，式(25)简化为：

(26)

式(26)推演结果说明，在由式(6)表示的核函数中恢复零阶和一阶项影响，即可确保由式(3)确定的扰动重力径向分量极限值δgr(r→R)收敛于球面上的理论预估值δgR.显然，这正是我们所期待的结果，但这里需要指出的是，式(26)只是理论上的理想化推证结果，在实际应用中，我们是无法完全按照式(20)—(23)的推证过程来实现扰动重力径向分量数值计算的.因为，选择一个无限小的球冠σ1既不现实也不符合数据实际，而当计算点与数据点重合时，在超低空高度段，由式(14)表示的积分核函数会出现非常严重的奇异性问题，从而导致式(12)的数值计算结果严重偏离预期的理论“真值”，这些都是由地球外部扰动位(类同于单层位)法向导数在边界面存在不连续性的固有特性和积分核函数(见式(14))具有与三维空间Dirac函数相似的跳跃特性所决定的(Heiskanen and Moritz,1967).

2.1.2 积分模型精密改化

由前面的分析得知，要想获得稳定且精确的扰动重力径向分量数值计算结果，除了需要对式(13)表示的核函数做零阶和一阶项恢复处理外，还需要对积分计算式实现过程中的核函数奇异性影响做进一步的改化处理.

根据式(1)—(3)、式(6)及式(11)—(15)，恢复零阶和一阶项影响后的扰动重力径向分量积分核函数Ftr(r,ψ)可表示为：

Ftr(r,ψ)=Fr(r,ψ)+Kr2(r,ψ)

(27)

不难看出，当r→R和ψ→0时，式(27)中的S(r,ψ)会出现分母项l→0，Kr1(r,ψ)可能出现分子分母同时为零(0/0)的不确定情况.为了消除此类核函数的奇异性影响，我们可参照Heiskanen和Moritz(1967)、黄谟涛等(2019)的研究思路，对以式(27)作为新的核函数的积分计算式(3)进行积分恒等式变换改化处理，可将其称为另一种形式的“移去-恢复”技术.首先，将式(3)改写为：

(28)

式中，ΔgRp代表外部空间计算点P(r,φ,λ)在球面上的投影点P(R,φ,λ)处的重力异常，也就是式(22)中的ΔgR.将式(27)代入式(28)右端的第二项积分，不难推得：

(29)

(30)

此时，式(28)可简写为：

(31)

不难看出，经上述移去恢复变换后，理论上，式(31)不再存在积分奇异性问题，至少可以说它的奇异性被中和了(Heiskanen and Moritz,1967).与此同时，当r→R时，顾及式(17)、式(23)和式(29)后，可推得由式(31)确定的径向分量δgr将收敛于球面上的理论预估值：δgRp=-2TRp/R-ΔgRp.这个结果说明，使用式(31)计算外部扰动重力径向分量，不仅可以避免奇异积分的影响，同时可确保积分计算值从地球外部到球边界面的连续性.

从前面的推导过程可以看出，如果不对原积分核函数式(6)做如式(27)所示那样的零阶和一阶项恢复处理，我们也无法实现式(29)和式(30)那样的第二步积分恒等式变换运算.由此可见，对于相同类别的地球外部重力场参数计算模型，包括外部扰动位、重力异常、重力梯度等积分模型，都需要在它们的原积分核函数基础上，恢复其零阶和一阶项的影响.只有这样，才能开展后续旨在消除积分奇异性和不连续性影响的改化处理.实际上，Heiskanen和Moritz(1967)利用Poisson积分公式和积分恒等式变换，对调和函数径向导数计算模型所做的去积分奇异性改化，正是建立在积分核函数事先包含了零阶和一阶项基础之上的.

需要指出的是，前面对式(3)所做的模型改化只是这一进程的第一阶段，受观测数据覆盖范围的限制，我们在应用式(31)时，还需要将全球积分域划分为近区和远区处理，近区定义为以计算点为中心、ψ0为半径的球冠区域σ0，以一定阶次(比如N阶)的重力位模型作为参考场，联合采用实测重力异常数据和移去恢复技术，对近区影响进行数值积分计算；远区影响则采用更高阶次(比如L阶)的重力位模型进行补偿.第二次引入“移去-恢复”处理模式后，还需要对积分核函数做相应的改化处理，以满足积分核函数与实测重力异常信息之间的频谱匹配要求(Novák and Heck,2002；刘敏等,2016).这里统一使用简单实用的Wong和Gore(1969)方法对积分核函数进行改化.经分区处理和核函数改化后，式(31)从全球积分模型改变为局域积分模型：

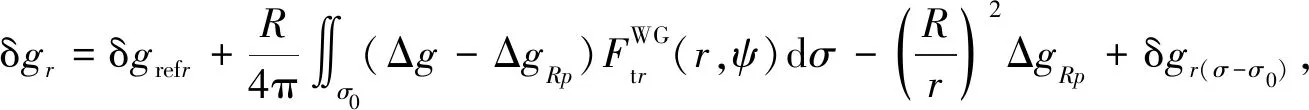
(32)

(33)

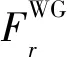
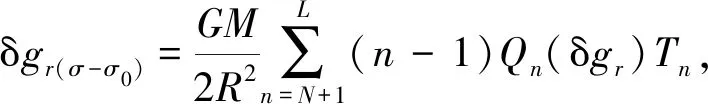
(35)

(36)

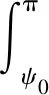
(38)

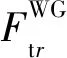
由前面的推证过程得知，式(28)能够过渡到式(31)是因为存在恒等式(29)和(30).值得注意的是，上述两个恒等式成立的条件是全球积分，当式(31)被改化为局域积分式(32)时，该条件不再满足，两个恒等式失效，故必须顾及非全球积分域对恒等式(29)和式(30)的影响，并在改化计算式(32)中加以补偿.不难看出，由全球积分过渡到局域积分引起的模型误差，就是计算点所在数据块重力异常ΔgRp作用于计算参量δgr的远区影响，其计算式为：

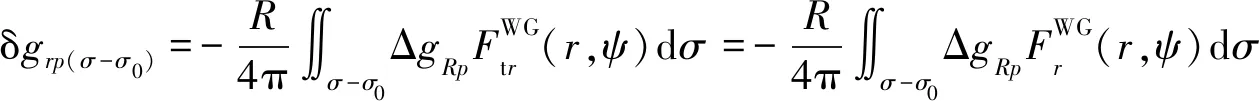
(39)

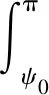
(41)

式中，δgrp(σ-σ0)代表ΔgRp在积分远区(ψ0-π)对计算参量δgr的影响.将式(6)代入式(40)，完成积分后可得：

(42)

(43)

(44)

(45)

(46)

将式(39)加入式(32)的右端，可得到计算外部扰动重力径向分量的严密改化公式：

+δgr(σ-σ0)+δgrp(σ-σ0).

(47)

在后面的数值计算试验中，我们将对远区修正量δgrp(σ-σ0)的大小做进一步的分析和验证.

2.2 水平分量积分模型改化

实际上，扰动重力水平分量全球积分模型同样面临相类似的适用性改化问题.首先，与径向分量相同，受观测数据覆盖范围限制，水平分量计算模型也需要将全球积分域划分为近区和远区处理(黄谟涛等,2019).为了减弱远区截断误差的影响，同样需要引入位模型参考场进行第二步移去恢复运算和核函数改化.略去具体推导过程，直接写出式(4)和式(5)从全球积分模型过渡到局域积分模型的改化公式如下：

(48)

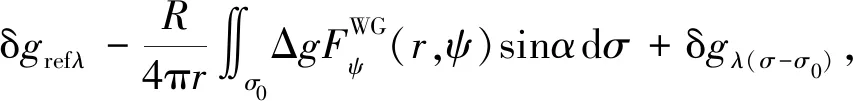
(49)

(50)

(51)

(52)

(53)

(54)

×Rn,m(ψ0),(55)

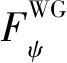
此外，由式(4)、式(5)和式(7)得知，当计算点与数据网格点完全重合时，该网格数据块对两个水平分量都不起作用，实施计算时可将其从积分域中扣除，以避免出现积分奇异性问题(黄谟涛等,2019).但是，当网格数据块的面积较大且计算点周围的重力异常场变化比较剧烈时，这种简单的处理方法可能会给计算结果带来毫伽(mGal=10-5m·s-2)级的误差.显然，对于高精度要求的扰动引力计算，这样的影响量仍不能忽略.为此，这里参照黄谟涛等(2019)的思路，进一步推出计算点所在数据块影响的积分计算式如下.

首先考虑到在计算点周围超低空高度段范围内，计算点与积分流动点之间的空间距离(l)相比地球平均半径(R)是一个很小的量，可将扰动重力水平分量积分核函数Fψ(r,ψ)(见式(7))做简化处理，只保留其中起主导作用的第一项：

(56)

假设与计算点重合的网格数据块半径为ψ00，因当前可使用的重力观测数据分辨率已经达到较高的水平，相对应的数据网格一般可达5′×5′甚至更小，故可进一步对式(56)表示的积分核函数做平面近似处理.这里以北向分量为例，依据式(48)，略去截断核函数式(52)右端的第二项影响，采用前面定义过的极坐标系(s,α)，可将与计算点重合数据块的积分式写为：

(57)

式中，s0代表数据网格大小的一半，当数据网格为1′×1′时，s0=0.5′.在此基础上，参照Heiskanen和Moritz(1967)的思路，将重力异常Δg在空间计算点P的球面投影点Rp处展开为泰勒级数：

+y2gyy)+…

(58)

式中，x轴指向正北，y轴向东，x=scosα，y=ssinα.并且有：

将式(58)代入式(57)，不难推得：

(59)

同理可得：

(60)

假设与计算点重合的数据格网为(i,j)，则可按(61)(62)式计算水平方向一阶梯度：

gx=[Δg(i+1)-Δg(i-1)]/(4s0),(61)

gy=[Δg(j+1)-Δg(j-1)]/(4s0cosφi).

(62)

将补偿计算式(59)和式(60)分别加到式(48)和式(49)的右端，就得到扰动重力水平分量的严密改化模型：

+δgφ(σ-σ0)+δgφ ψ00,(63)

+δgλ(σ-σ0)+δgλ ψ00,(64)

式中，(σ0-ψ00)代表扣除计算点所在网格数据块后的近区.

3 数值计算检验与分析

3.1 数值检验使用的数据及区域

为了分析验证前面提出的地球外部扰动重力三分量全球积分模型的改化效果，本文采用超高阶位模型EGM2008作为数值计算检验的参考标准场(Pavlis et al.,2012)，用于模拟产生地球表面(近似为球面)1′×1′网格重力异常观测量“真值”及地球外部不同高度面上的1′×1′网格扰动重力三分量理论“真值”(这里使用1′×1′而非5′×5′网格数据是为了减弱积分离散化误差的影响).由地球位模型计算外部扰动重力三分量的公式参见式(33)、式(50)和式(51)，计算球面重力异常的公式参见黄谟涛等(2005).

为了说明检验结果的代表性，这里特意选取重力异常场变化比较剧烈的马里亚纳海沟作为试验区，具体覆盖范围为：6°×6°(φ:10°N—16°N；λ:142°E—148°E).首先选取截断到360阶次的位模型EGM2008作为参考场，即取N=360，然后选取361～2160阶次的位模型EGM2008作为数值计算检验的标准场，即取L=2160，由该标准场模型计算球面上的1′×1′网格重力异常观测量“真值”Δgt；进而选取ri=R+hi，R=6371 km，使用标准场模型EGM2008(361～2160阶次)分别计算对应于9个高度面上的1′×1′网格扰动重力三分量理论“真值”δgtri、δgt φ i和δgt λ i(i=1,2,…,9),每个高度面对应360×360=129600个网格点数据，9个高度分别取为：hi=0 km,0.1 km,0.3 km,1 km,3 km,5 km,10 km,30 km,50 km.表1列出了其中的4个高度面上的扰动重力三分量理论“真值”和球面上的重力异常观测量“真值”的统计结果，图1—4分别给出了球面重力异常观测量“真值”和对应于零高度面上的扰动重力三分量理论“真值”分布态势图.

表1统计结果和图1—4显示的重力参数曲线变化形态说明，尽管已经扣除掉2～360阶次频段的位模型参考场，本试验区域重力异常场变化的激烈程度仍然比较显著，可在一定程度上代表真实地球大部分局部重力场的变化特征.

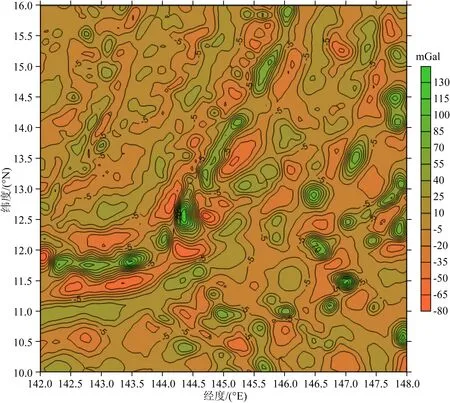
图1 重力异常分布图Fig.1 Distribution of the gravity anomalies

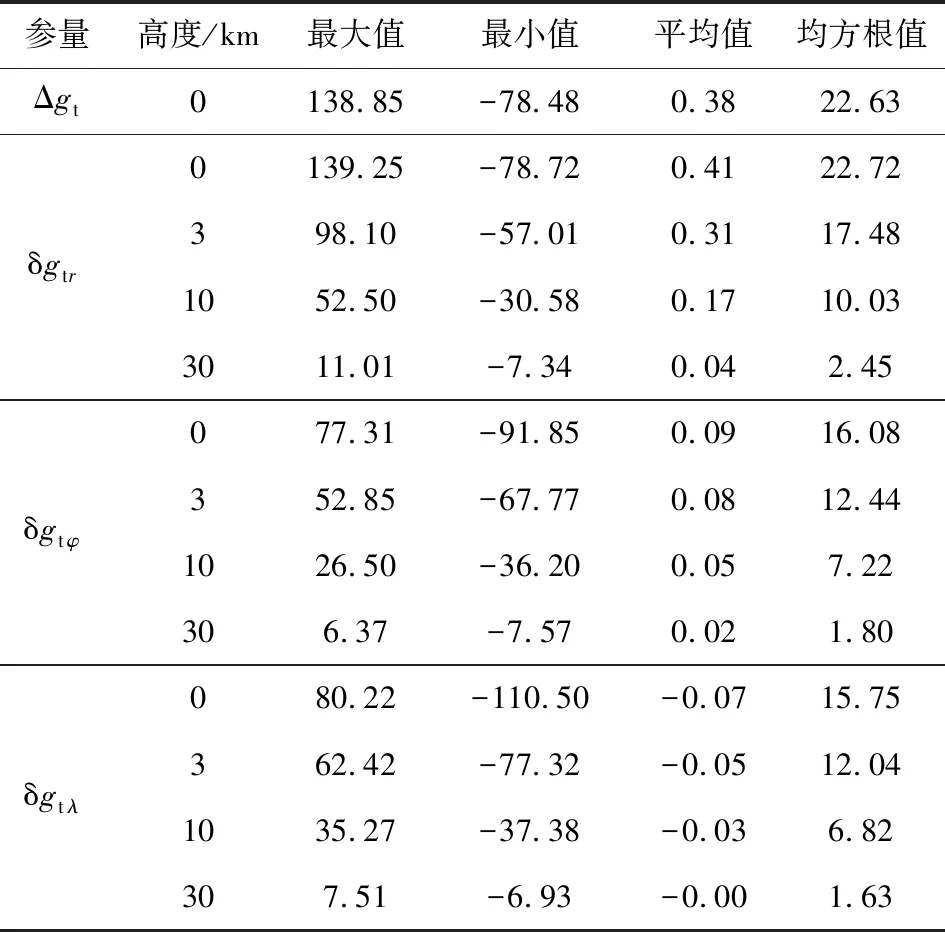
表1 由EGM2008模型(361～2160阶次)计算得到的重力异常和扰动重力统计结果(单位：mGal)Table 1 Statistics of gravity anomalies and disturbing gravities obtained by the EGM2008 model of degree 361～2160(unit:mGal)

3.2 改化模型数值检验方法及结果分析

为了对比分析前述不同阶段扰动重力三分量改化模型的计算效果，这里采用球面上的1′×1′网格重力异常“真值”Δgt作为观测量，同时使用径向分量3种改化模型和水平分量2种改化模型，对前面选定的试验区对应于9个高度面上的1′×1′网格扰动重力进行计算分析，其中，径向分量第1模型是指直接使用式(3)作为基础计算模型，并对全球积分域做了分区处理，但在实施近区计算时，扣除掉计算点所在的1′×1′数据块，以避免出现奇异积分问题；第2模型对应于公式(32)；第3模型对应于公式(47)；水平两个分量第1模型是指直接使用式(48)和式(49)作为基础计算模型，但在实施近区计算时，扣除掉与计算点重合的1′×1′数据块；第2模型对应于公式(63)和式(64).将三分量对应于前述各阶段改化模型的计算值分别与相对应的理论“真值”δgtri、δgtφi和δgtλi做比较，可获得不同改化模型的精度评估信息，具体比对结果列于表2.这里积分半径统一取为ψ0=2°，为了减小积分边缘效应对评估结果的影响，表2只列出中心区2°×2°方块内的比对结果(下同).为了定量评估由全球积分过渡到局部积分引起的径向分量模型误差和由计算点所在网格重力异常变化引起的水平分量模型误差影响，表3给出了采用式(39)计算得到的两组分别对应于积分半径ψ0=2°和ψ0=5°的误差补偿量δgrp(σ-σ0)及采用式(59)和式(60)计算得到的误差补偿量δgφ ψ00和δgλ ψ00的统计结果.

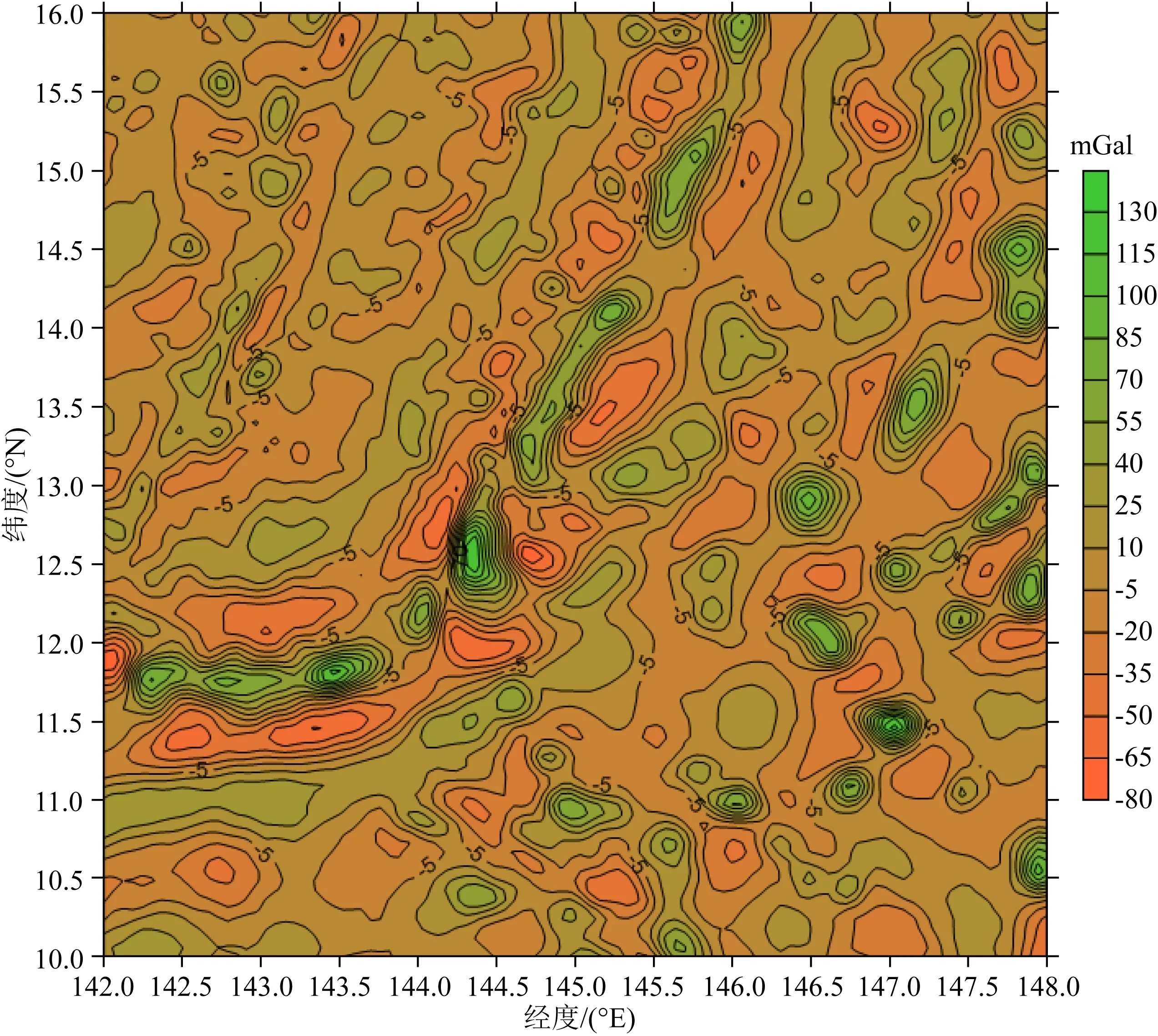
图2 扰动重力径向分量分布图Fig.2 Distribution of the radial components of disturbing gravity

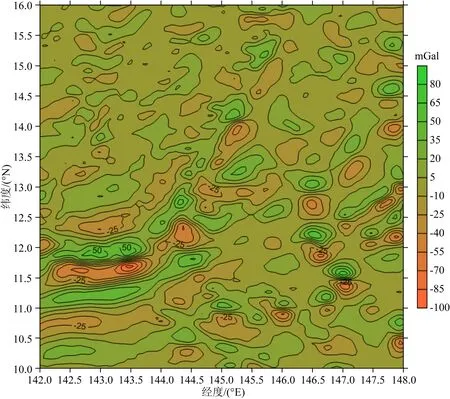
图3 扰动重力北向分量分布图Fig.3 Distribution of the north components of disturbing gravity

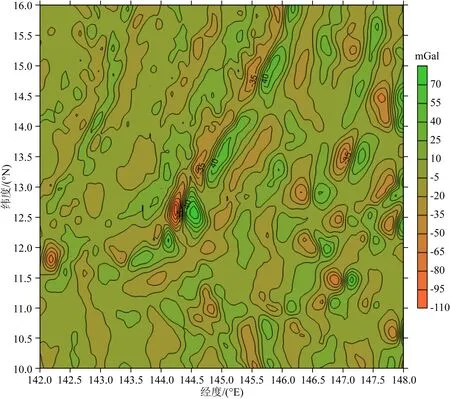
图4 扰动重力东向分量分布图Fig.4 Distribution of the east components of disturbing gravity

从表2比对结果可以看出，不同阶段改化模型的计算精度存在较大差异，径向分量的差异尤为明显.表面上看，径向分量第1模型的误差是由于直接扣除了计算点所在数据块的影响引起，实质上是原始积分模型在边界面存在不连续性所致.对比表2和表1结果可以看出，第1模型在超低空高度段的误差量值甚至超过了径向分量自身大小，显然，这不是忽略计算点所在数据块影响所能引起的量值，而是正如式(23)所显示的那样，当r→R时，第1模型的原始计算式(3)存在与边界面重力异常ΔgR大小大致相等的数值跳跃所致，与我们前面所做的理论分析预期相吻合.这个结果说明，径向分量原始计算模型在超低空高度段是失效的，只有在5 km以上计算高度才是可用的.第2模型是对第1模型的改化，从理论上消除了积分奇异性和数值不连续性影响，并在超低空高度段取得了比第1模型好得多的计算精度，但由于该模型的改化过程存在不可忽略的理论缺陷，在3 km以上高度，该模型的计算精度反而不及第1模型，即使到了10 km高度，该模型的比对中误差仍然超过不可接受的2 mGal.第3模型从理论上弥补了第2模型的缺陷，使得该模型的计算精度得到显著改善，在所有9个高度面，该模型计算值与比对基准“真值”的最大互差均不超过1.2 mGal，互差均方根值不超过0.4 mGal.这个结果说明，我们对第2模型所做的补偿改化处理是正确和有效的.两个水平分量第1和第2改化模型的区别主要体现在，后者比前者增加了计算点所在数据块的影响.表2结果显示，相比第1模型，第2模型计算精度在300 m以下超低空高度段的提高幅度比较明显，从毫伽级提升到1 mGal以内，充分体现了该模型的改化效果.可以预见，当采用的数据网格间距加大(比如从1′×1′增大到2′×2′)且计算点周围的重力异常场变化更为剧烈时，第2模型的改化效果会更加显现.这里需要指出的是，本试验是在一个重力位标准场中进行的，表2统计结果反映的只是单一的计算模型误差影响，不包含数据传播误差，也不包含受限于数据分辨率的数据截断误差.另外，对比表2中的径向分量和水平分量精密改化模型的计算效果可以看出，前者的总体精度要略优于后者，这说明积分模型离散化误差对后者的影响要略大于前者.

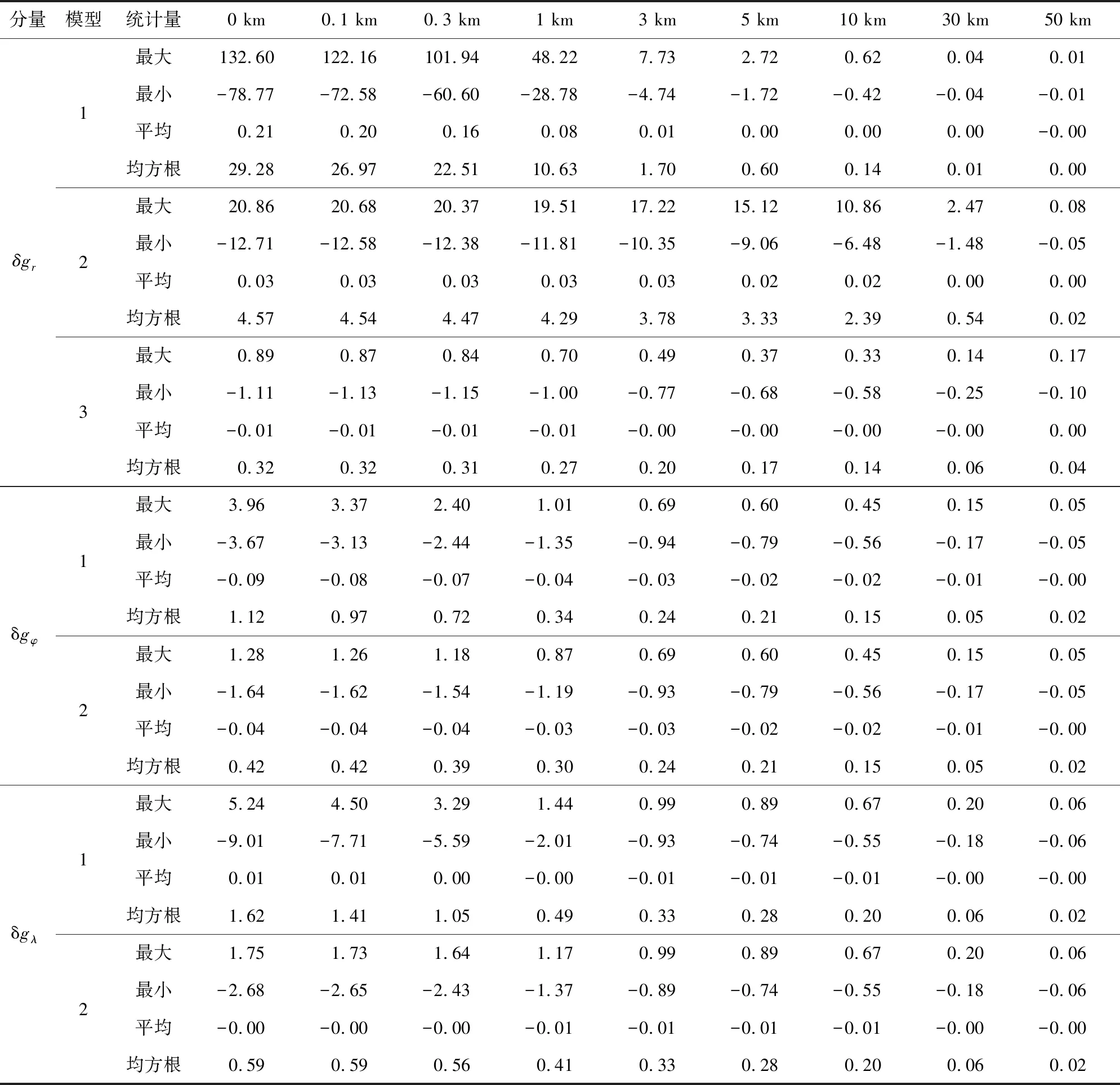
表2 由不同改化模型计算得到的9个高度面扰动重力三分量与“真值”的比较(单位：mGal)Table 2 Differences between the three components of disturbing gravity,obtained by different modified models,and the “true values”on 9 altitude surfaces (unit:mGal)

由表3计算结果可进一步看出，尽管径向分量第3模型对第2模型的补偿量均随参考场阶数N、积分半径ψ0和计算高度h的增大而减小，但当参考场阶数取为N=360时，即使积分半径增大到ψ0=5°，计算高度h=10 km处的误差补偿量均方根值仍然超过1 mGal.在超低空高度段，两个水平分量的误差补偿量也都超过1 mGal.不难推断，如果取参考场阶数为N=180，那么，相同高度上的误差补偿量还会增大.这样的结果再次说明，对于高精度要求的地球外部重力场赋值，对传统计算模型进行精细改化是非常必要的.

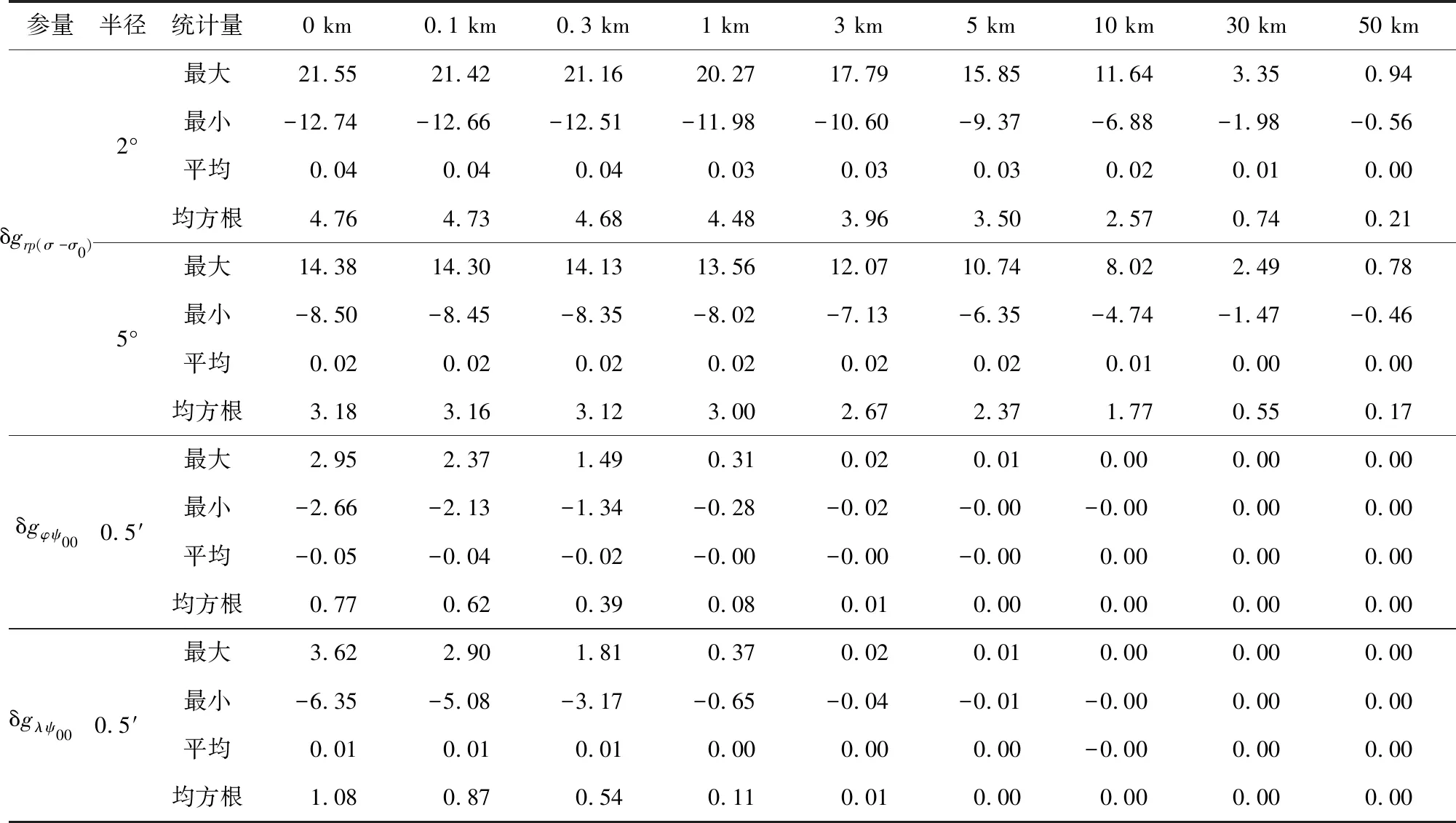
表3 模型误差补偿量δgrp(σ-σ0)，δgφ ψ00和δgλ ψ00计算结果统计(单位：mGal)Table 3 Statistics of the computational results of error compensation δgrp(σ-σ0),δgφ ψ00 and δgλ ψ00 (unit:mGal)

为了考察数据观测误差对改化模型解算结果的影响，在前述试验基础上，进一步开展有输入数据噪声影响条件下的数值计算检验.具体做法是，在前面作为观测量的位模型剩余重力异常“真值”Δgt中分别加入1 mGal和3 mGal的随机噪声，形成两组新的模拟观测量，然后按照前面相同的计算方案和流程，依次采用前述(3+2+2)种改化模型完成9个高度面上的1′×1′网格扰动重力三分量计算，最后将计算结果与相对应高度的三分量“真值”做比对评估，具体评估结果如表4所示.为节省篇幅，这里只列出其中的比对互差均方根值(RMS).

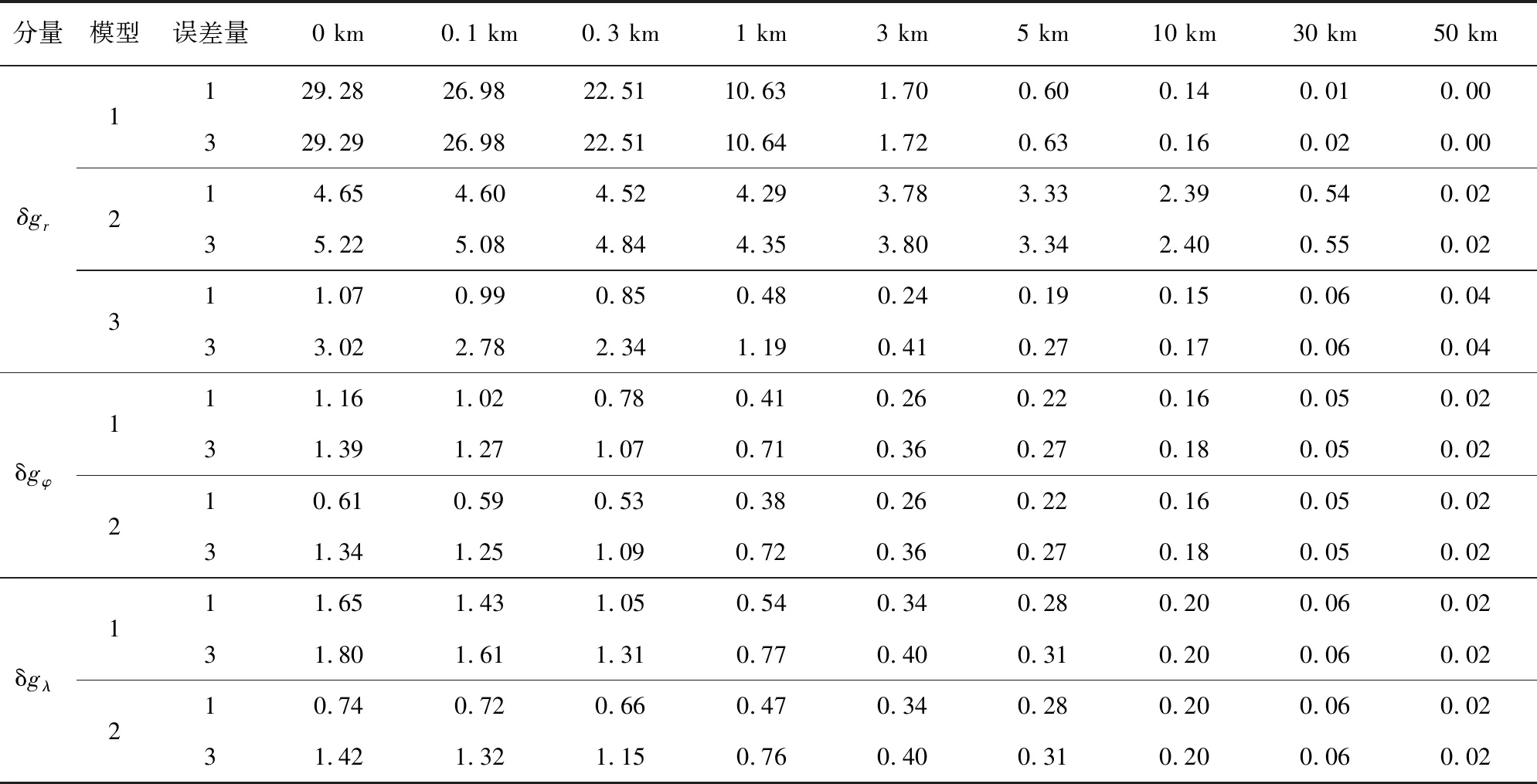
表4 误差影响下由不同改化模型计算得到的9个高度扰动重力三分量与“真值”的互差均方根值(单位：mGal)Table 4 RMS of the differences between the three components of disturbing gravity,obtained by different modified models with noisy data,and the “true values”on 9 altitude surfaces (unit:mGal)

从表4统计结果可以看出，数据噪声对7种改化模型解算结果的影响规律是一致的，没有因为模型改化形式的不同而产生实质性差异.总体而言，数据误差只对5 km高度以下的计算结果产生一定程度的影响.对比表4和表2计算结果不难看出，1 mGal数据噪声对各个改化模型解算结果的影响很小，几乎可以忽略不计；3 mGal数据噪声对径向分量第1和第2模型、两个水平分量第1模型的影响相对较小，对径向分量第3模型、两个水平分量第2模型的影响相对较大.这是因为在前面的近似改化模型中，相对于数据误差，模型误差的影响明显占主导地位；而在后面的精密改化模型中，情况正好相反，模型误差减小后，数据误差影响起了主导作用.这些结果说明，即使采用严密的径向分量第3模型和水平分量第2模型进行外部扰动重力计算，也要尽可能将数据观测误差控制在较低的水平.

4 结论

为了提高地球外部重力场的赋值精度，本文分析研究了外部扰动重力Stokes全球积分计算模型的技术特点和适用条件，指出了扰动重力径向分量积分模型在边界面存在不连续性的原因，同时提出了保持其连续性的修正方法.为了消除全球积分模型向局域积分转换中遇到的积分奇异性问题，综合采用移去恢复运算和积分恒等式变换技术，同时依据实测数据保障条件，分别推出了地球外部扰动重力三分量积分模型的分步改化公式，提出了补偿传统改化模型缺陷的修正公式.采用超高阶地球位模型EGM2008建立比对标准重力异常场，同时选择在重力异常场变化比较剧烈的马里亚纳海沟区块开展数值计算符合度检验，分别对本文推出的扰动重力径向分量3种分步改化模型和水平分量2种分步改化模型的计算精度进行了检核分析和评估.试验结果表明，采用最终的严密改化模型不仅可以有效消除原计算模型固有的积分奇异性，又可显著提高超低空扰动重力三分量的计算精度和稳定性.因此，新的严密改化模型具有较高的推广应用价值，可用于地球外部全高度段扰动重力场的高精度赋值.