统计降尺度方法在天津小时降水和气温精细化预报中的应用

田 笑，余文韬，从 靖，周红梅

(1.天津市气象台，天津 300074；2.江苏省东台市气象局，江苏 东台 224200)

引 言

随着大城市人口快速增长、人民生活质量不断提高，不仅从国家战略层面还是人民生产生活上，对时间和空间上更为精细准确、要素更为多样化的天气预报需求日趋紧迫。现代天气业务的建立和天气预报技术的发展，也需要实现天气预报精细化。我国各省气象台已全部推行精细化预报制作，需要3 d内逐小时分辨率的精细化格点预报，为了提高预报准确率和减小主观订正的工作量，精细化预报系统需要同样精细的气象要素客观预报底板数据支撑。

当前可以从两个方面发展精细化预报，一是研发更高时空分辨率的数值预报模式，另一个就是采取降尺度方法。以目前的科学条件，提升模式的分辨率不仅计算量很大，而且技术也较复杂，还做不到任意提高全球或者区域数值模式的时空分辨率。降尺度方法可操作性较强、计算量较小，在气象业务单位中更易实现，因此开展降尺度研究显得十分重要[1]。现有的降尺度方法大致可分为统计降尺度法[2-3]和动力降尺度法[4]。建立大尺度预报因子与小尺度预报量之间的统计函数关系是统计降尺度法的基本思想。其优点是不需考虑边界条件对预报结果的影响，能将模式结果中物理意义较好、准确率较高的数值预报产品应用于统计模式，从而减少数值模式的系统性误差。相较于动力降尺度法，统计降尺度方法还有计算量较小、可模拟很多非气象要素场等优点，在科研和实际业务中更具可操作性。近年来，统计降尺度法主要集中应用在温度和降水预报等方面[5-12]。现有的统计降尺度法大致可分为环境分型技术、天气发生器和转换函数法3种[13-14]。前2种方法常应用于时间尺度较长的气候场，而转化函数法广泛应用在精细化预报中。近年来国内将统计降尺度方法应用于中短期天气预报的还不多见，主要集中在对时间尺度较长的未来区域气候情景变化的预估方面。如高红霞等[15]对华东地区的月平均气温进行统计降尺度，发现四季温度因子都优于环流因子，预报因子的区域选择对降尺度效果有一定影响，多元线性回归的统计降尺度方法相较于3种主成分分析法，对单站温度的年际变化模拟方面有一定优势；范丽军等[16]采用逐步回归分析与主分量分析相结合的多元回归方法建立华北地区月平均气温统计降尺度模型，发现统计降尺度处理后的气温预报与观测值具有很好的一致性，但相比观测值略微偏低；另外基于卡尔曼滤波类型的自适应递减平均降尺度方案对中国日均气温的预报研究表明，该方法显著减小了东西部预报效果差异，并且预报效果夏季优于冬季[17-18]；用BP神经网络和多元线性回归两种降尺度方法对深圳地区近10 a的日最低、最高气温的预报比较发现，神经网络模型的训练样本拟合情况要好于多元线性回归，但检验样本的拟合情况却相反，对最低气温的拟合效果好于对最高气温的拟合效果，冬季气温的模拟效果好于夏季[19]；基于全球交互式大集合(THORPEX interactive grand global ensemble， TIGGE )预报资料和TRMM/3B42RT合成降雨量资料，对1～7 d的降水预报进行统计降尺度试验，发现单个中心的预报场经过统计降尺度后，与“观测场” 的距平相关系数明显提高，并且预报误差明显减小[20]；唐文苑等[12]通过时间滞后集合预报方法进行降水量级订正，24 h内逐小时降水量预报结果表明对我国江南南部、华南、西南地区效果明显，中小尺度强降水过程的降水系统位置、形态及降水量级的预报水平都有明显提高。

以上研究表明，统计降尺度方法处理后对于降水和温度的预报均有明显提高，但在1～3 d的1 h精细化预报方面研究还很缺乏，尤其适用于业务应用的更少。为进一步提高大城市气象要素精细化预报的预报质量，减小预报员制作预报过程中的主观订正工作量，本文尝试采用多种统计降尺度方法，结合近300个自动观测站资料，探讨统计降尺度方法在天津市1 h降水和地面气温精细化预报中的应用。

1 资料与方法

1.1 资 料

所用模式资料为2018年3月1日至11月30日的ECMWF细网格预报资料，预报时效为1～96 h，时效间隔1 h。观测资料为天津市292个气象站点的逐小时资料。

1.2 统计降尺度方案

(1)预处理

为了使时空分辨率保持一致，对预报资料的空间处理采取双线性插值法插值，将预报的格点插值到天津市292个站点上，对预报资料的时间处理采取普通的线性插值，将预报的逐3 h资料插值成逐1 h。

(2)降水订正法

利用频率匹配法进行插值后的误差订正。其基本思路是通过计算训练期内ECMWF模式预报不同阈值降水量的订正系数，将其应用于预报期的降水量预报订正。由于天津汛期在6—8月，为了有足够的样本数而又大致考虑到近期相似的总天气形势，降水的训练期选取预报日的前30 d，预报期资料为62 d (7月1日至8月31日)。

利用阈值法对频率匹配法订正后的结果再进一步减小空报率。对于观测无雨、模式预报有雨(一般是少量降水)的格点而言，频率匹配法无法将降水量消除为零，所以采用阈值法消除空报的样本。首先，选定某一时刻的某一个格点，列出训练期中该点观测与预报的所有降水量,挑选出实际观测无雨时对应的模式预报降水量(即空报降水的样本)，按照降水量从小到大的顺序排序；其次，按照一定的百分比设定一个临界值，该时刻之后的预报降水量低于该临界值就算无雨，降水量为0。

(3)温度订正法

CUI等[21]2011年提出了一种具有自适应特征的Kalman滤波型的递减平均统计降尺度技术，并用该方法对北美集合预报系统的输出值做后处理，获得精细化预报产品，取得明显效果。该方法现已在NCEP的精细化预报中实现了业务化应用。李莉等[22]和邱学兴等[23]应用这种类卡尔曼滤波的递减平均统计降尺度技术分别对T213集合预报产品和T639预报产品进行了误差订正研究，取得了较好效果。

本文基于Kalman滤波型的递减平均误差统计降尺度技术对预报结果逐点进行订正。

首先，需要计算某一格点训练期内每一天模式预报的误差；其次，按照一定的权重迭代将前一时刻的递减平均误差计算到下一时刻的递减平均误差中：Bt=(1-W)Bt-1+Wbt，Bt是t时刻的递减平均误差，W是递减权重系数，bt是t时刻误差；最后，在下一时刻的模式预报中扣除通过历史资料算出的递减平均误差。

这样的自适应迭代构造递减平均误差，不仅突出了模式近期的误差水平，又反映了一段时间的平均误差水平。订正方案实施中，既要考虑温度的连续性又要考虑到温度的月、季变化，温度训练期资料选取预报日的前50 d，预报期资料为275 d (3月1日至11月30日)。

(4)滑动训练

滑动训练期表示用于建模的资料不固定，通过所需改进预报之前一段时间的预报资料与观测资料进行训练，得出相应的参数应用到原始预报中，进而得出相应的订正预报。由于不涉及所需改进预报对应的观测资料，该方法可应用于资料实时更新的精细化预报系统中，相比于交叉检验更具有实际应用意义。

1.3 误差检验标准

(1)降水检验

因1 h累计降水量和24 h累计降水量差别很大，所以不能用24 h累计降水的小、中、大雨划分标准来检验，这里给出的1 h晴雨预报、1 h强降水预报TS评分、1 h降水量预报平均相对误差的检验方法，引用自2021年智能预报技术方法竞赛检验方案(1)预报司.《关于印发第八届全国气象行业天气预报职业技能竞赛智能预报技术方法单项实施方案的通知》，附件2：智能预报技术方法竞赛检验方案，2020年7月。

①晴雨预报准确率

晴雨预报准确率指降水量阈值为0.1 mm时，无雨和存在有效降水(大于等于0.1 mm)时预报准确的站(次)总数与预报区域的总站(次)数的比值。公式如下：

(1)

式中：NA、NB、NC分别为降水预报正确、空报和漏报的站(次)数；ND为无降水预报正确的站(次)数。

②强降雨TS评分

强降水预报TS评分指1 h降水大于等于20 mm时，预报准确的站(次)总数与预报区域的总站(次)数比值。公式如下：

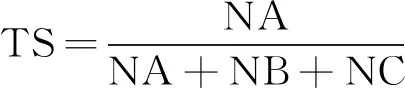
(2)

③降水的平均相对误差

(3)

式中：Rob为观测降水量，Rfo为对应的预报降水量。当实况和预报值都为0时，相对误差计为0。

(2)温度检验

用平均绝对误差进行检验，公式如下：

(4)

式中：Fi为第i站(次)预报温度；Oi为第i站(次)实况温度；N为参评站点数。

文中附图所涉及地图基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2017)1267的标准地图制作，底图无修改。

2 统计降尺度在降水精细化预报中的应用

2.1 对1 h降水预报的评估

图1是1～96 h时效1 h累计降水的模式预报与订正后的晴雨预报准确率对比。可以看出，ECWMF模式晴雨预报准确率随预报时效延长呈波动性减小，曲线波动周期约为24 h。频率匹配法提高了绝大多数预报时效的晴雨预报准确率，明显改进了降雨预报技巧，最大改进幅度可达20%以上。订正后的晴雨预报曲线也具有随预报时效延长呈波动性下降趋势，且波峰、波谷与订正前位置基本一致，说明频率匹配法订正效果与订正前预报的优劣有一定的关系。利用阈值法二次订正后，晴雨预报在多个预报时效有一定提升，提升最大时可超过90%，但是阈值法只针对空报情况，也没有考虑实际降水的分布情况，所以阈值法订正后的晴雨预报曲线效果和订正前预报的优劣没有一定的关系，且在有些时候会把应有的降水订正成无雨，导致晴雨预报准确率反而下降。

图1 2018年7月1日至8月31日1～96 h时效1 h累计降水的ECMWF模式预报(蓝线)，频率匹配法订正后(红线)及二次订正后(绿线)的晴雨预报准确率曲线

图2是1～96 h时效1 h累计降水的模式预报与订正后的平均相对误差对比。可以看出，和晴雨预报准确率类似，ECWMF模式预报的降水相对误差曲线随预报时效延长具有波动性，相对误差曲线的波峰(波谷)大致对应晴雨预报准确率曲线的波谷(波峰)。频率匹配法对相对误差的改进效果微小，但是经过阈值法二次订正以后，相对误差明显下降，说明阈值法对空报现象有较明显改进。

图2 2018年7月1日至8月31日1～96 h时效1 h累计降水的ECMWF模式预报(蓝线)及频率匹配法订正后(红线)和二次订正后(绿线)的平均相对误差曲线

图3是1～96 h时效1 h累计降水大于等于20 mm的短时强降雨的模式预报与订正后的TS评分对比。整体上看，经过频率匹配法订正后的TS评分显著高于模式预报的TS评分，偶尔也会出现订正后TS评分下降的时效。TS评分曲线中出现多处TS评分为0或无效值的窗区，这主要是因为小时累计雨量在20 mm 以上量级的降水出现几率低，并且降雨落区更难把握，这个特点在降水偏少的华北地区很明显[12]。

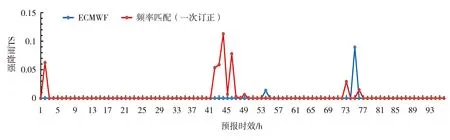
图3 2018年7月1日至8月31日1～96 h时效1 h强降水(大于等于20 mm)的ECMWF模式预报(蓝线)和频率匹配法订正后(红线)的TS评分曲线

2.2 在2018年“安比”台风事件中的应用

通过上节分析可知，频率匹配法和阈值法订正后的ECWMF模式降水预报各项评分都有明显提高，但是这些评分是基于长时间平均的统计结果，对降水预报的评估还需分析一些典型强降水个例的预报技巧。本文选取一次强台风造成的强降水个例，对模式预报强降水的技巧进行评估。

台风“安比”是1972年以来首个进入且直接经过天津的台风，天津遭遇建国以来最大台风雨，2018年7月23日20：00(北京时，下同)至24日16：00，天津全市平均降水119.2 mm，市区平均降雨量179.7 mm，局地雨量最高达 237.1 mm。

图4为2018年7月23—24日1～96 h时效1 h累计降水的ECMWF模式预报与订正后的晴雨预报准确率对比。可以看出，频率匹配法订正后，晴雨预报准确率在多数预报时效都有所提高。经过阈值法二次订正后，准确率再次提升，与之前类似，阈值法订正后的晴雨预报曲线效果和订正前预报的优劣没有一定的关系。

图4 2018年7月23—24日1～96 h时效1 h累计降水的ECMWF模式预报(蓝线)及频率匹配法订正后(红线)和二次订正后(绿线)的晴雨预报准确率曲线

从图5看出，频率匹配法对模式预报降水的相对误差改进效果甚微。但是经过阈值法二次订正以后，相对误差明显下降。可能是模式对强系统性降水过程的预报准确率较高，相应地频率匹配法的改进效果较好但幅度有限，阈值法对一般降水的空报现象有较大幅度的改进。

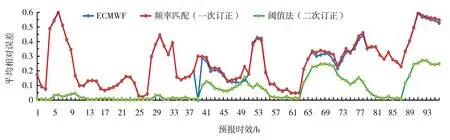
图5 2018年7月23—24日1～96 h时效1 h累计降水的ECMWF模式预报(蓝线)及频率匹配法订正后(红线)和二次订正后(绿线)的平均相对误差曲线

图6是7月23—24日1～96 h时效1 h累计降水大于等于20 mm的短时强降雨的模式预报与订正后的TS评分对比。由于只订正了2 d，训练期较短，TS评分曲线中出现更多处TS评分为0或是无效值的窗区。整体上看，经过频率匹配法订正后的TS评分明显高于模式预报的TS评分，偶尔也会出现订正后TS评分下降的时效。

图6 2018年7月23—24日1～96 h时效1 h强降水(大于等于20 mm)的ECMWF模式预报(蓝线)和频率匹配法订正后(红线)的TS评分曲线

选取天津降水最强时段的预报效果进行评估分析。7月24日06：00降水量实况[图7(a)]显示，降水主体位于天津中南部，呈东北—西南向分布，最大降水中心位于天津市区，降水量在20～30 mm，次中心位于北部，最大降水量在10～20 mm，个别站降水超过20 mm。对比模式预报情况，模式预报降水量级偏小，全区降水量均低于20 mm，降水主体位于中部范围，降水空间分布预报不太准确，未体现出降水主体形状，也未体现出蓟州北部山区次大降水中心[图7(b)]。通过频率匹配法订正后，虽然降水主体位置仍存在较小偏差，但是降水量级和主体形态调整后与实况基本吻合；虽然北部山区降水中心仍未体现，但是北部蓟州降水量级提高到了10～20 mm[图7(c)]。阈值法二次订正后，4个空报站全部预报正确，并且也没有过度订正[图7(d)]。

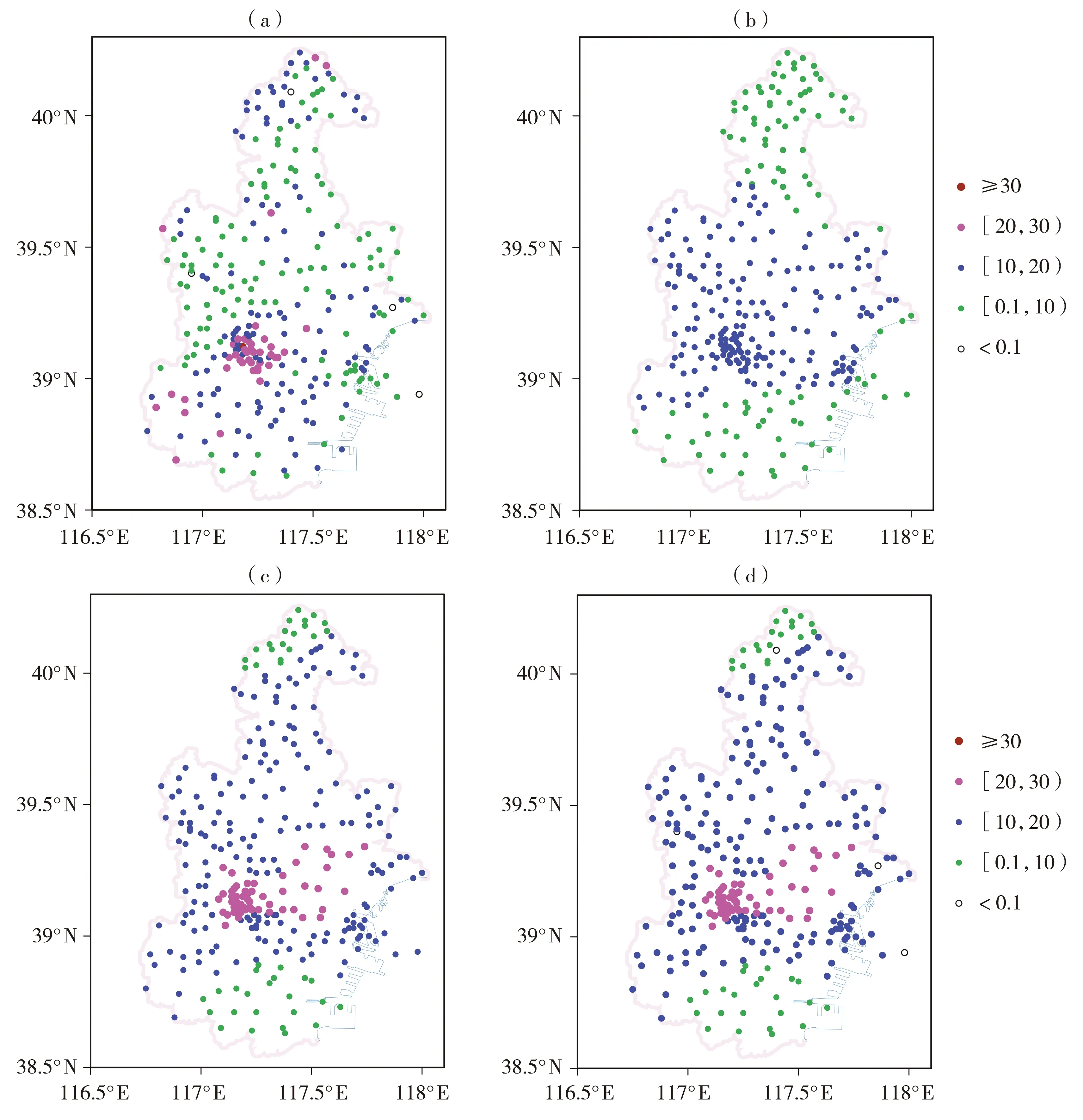
图7 2018年7月24日06：00降水实况(a)，ECMWF模式7月22日预报的34 h时效降水预报(b)及频率匹配法订正(c)和二次订正(d)后的降水空间分布(单位：mm)

3 统计降尺度在气温精细化预报中的应用

3.1 对1 h气温预报的评估

以温度预报的绝对误差作为衡量预报效果的指标，逐月计算2018年3—11月ECWMF模式1～96 h预报时效在天津地区的区域平均绝对误差。从图8看出，由于温度的连续性，插值后的温度绝对误差曲线也基本连续顺滑，并且绝对误差随预报时效延长呈周期性波动增大趋势，周期约为24 h。另外几乎在任何预报时效内都是3月的绝对误差最大。订正后的绝对误差曲线仍具有周期波动性，波峰、波谷位置也与降尺度前基本一致，且绝对误差越大，订正后减小越明显。

春季[图8(a)] ，3月绝对误差最大，5月最小。3月9 h 预报时效以内绝对误差在2 ℃范围内，58 h预报时效后绝对误差超过3 ℃，个别时效超过4 ℃；4、5月的绝对误差几乎都在3 ℃以内，60 h预报时效以内有时还低于2 ℃。另外，春季3、4、5月绝对误差曲线波动周期内的波峰、波谷位置基本一致，说明模式可能对这3个月的温度预报性能相似。进行统计降尺度后，绝对误差都有较明显减小，3月改进最大，有时改进1 ℃以上。随着预报时效延长，改进幅度有减小趋势，5月的87 h预报时效后有几个时效降尺度后绝对误差反而增大。

夏季[图8(b)]，6月绝对误差最大，8月最小，且整体的绝对误差小于春季。7、8月绝对误差曲线的波峰、波谷位置基本一致，但与6月差别较大，7、8月的绝对误差多数在2 ℃以内，6月绝对误差范围和4、5月一致。说明模式可能对7、8月的温度预报性能相似且稳定。进行统计降尺度后，绝对误差减小不明显，最大改进幅度只有0.4 ℃，且6月几乎没有减小。

图8 2018年春季(a)、夏季(b)与秋季(c)的1～96 h时效1 hECMWF模式温度预报统计降尺度前(虚线)、后(实线)的平均绝对误差

秋季[图8(c)]，ECWMF模式对温度的预报情况与春、夏季有所不同，绝对误差多数在2 ℃以内，虽然误差曲线仍具有较明显的波峰、波谷，但与前两季相比平缓了很多，说明模式的预报性能基本一致且更加稳定。进行统计降尺度后，绝对误差都有了较明显减小。

3.2 在2018年4月3日降温事件中的应用

选取2018年4月初一次寒潮过程，对模式预报温度的技巧进行评估。4月2日天津市区及中南部地区最高气温在30 ℃以上，其中市区、西青区和津南区的最高气温达33 ℃。4月3日白天气温大幅下降，市区白天最高气温由2日的33 ℃下降至12.9 ℃，全市最低气温下降幅度在8.3～15.4 ℃之间，宝坻、宁河达到寒潮，其他地区为强寒潮或特强寒潮。4月4日早晨出现极端最低气温(北辰区-1 ℃)，4月4—6日连续3 d全市白天最高气温均低于10 ℃。此次过程前期先出现了历史同期极端高温，后又出现寒潮过程，温度变化剧烈，预报难度大，ECWMF模式预报效果较差。

图9为ECMWF模式3月31日和4月1日预报的1～96 h时效内逐小时天津地区2 m气温在统计降尺度前后的平均绝对误差。由于温度的连续性，插值后的温度和温度绝对误差曲线也基本连续顺滑，并且绝对误差随预报时效延长呈波动性增大，与业务预报基本一致。进行统计降尺度后，绝对误差都有了较明显的减小，且减小后的绝对误差曲线仍具有周期性波动，波峰、波谷位置也与降尺度前基本一致。除了4月3日18：00前后(3月31日预报71 h时效，4月1日预报47 h时效)，可能误差过大超出订正范围，可以看出绝对误差越大，统计降尺度后减小幅度越大，一些时次订正幅度达30%以上。也可以看出，模式预报具有跳跃性，不一定越临近的预报越准确，3月31日预报的绝对误差与4月1日相近，一些时次3月31日预报的误差甚至更小。同样，对模式预报的订正也是在模式的预报效果基础上进行，所以也不完全是越临近预报的订正幅度越大。

图9 2018年3月31日(a)与4月1日预报(b)的1～96 h时效1 h ECMWF模式温度预报统计降尺度前(虚线)、后(实线)的平均绝对误差

此次过程4月2日夜间至4月3日全市出现东北风5～6级，4月3日白天气温大幅下降，白天最高气温出现在08：00。图10为4月3日08：00天津全市温度分布实况，3月31日ECMWF模式对该时次的预报和统计降尺度后的温度分布和温度绝对误差分布。可以看出模式预报和实况空间分布一致，均是北部和东部较低，中南部较高，市区最高。但是从绝对误差分布来看，整体误差都较大，其中北部、东部误差较小，中部、东北部和东南部误差较大，尤其市区误差较大，看来北部山区地形对这次预报影响较小，而城市效应对温度预报的影响较大。统计降尺度订正后，全市大部分地区绝对误差下降到2 ℃以下，一半区域下降到1 ℃以下，尤其市区改进明显，并且温度的空间分布仍和实况保持一致。

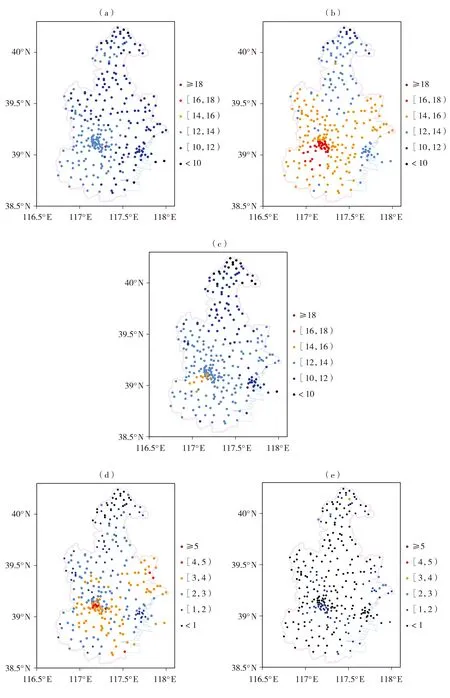
图10 2018年4月3日08：00天津气温分布实况(a)， ECMWF模式3月31日预报的4月3日08：00统计降尺度前(b、d)、后(c、e)的气温分布(b、c)和绝对误差分布(d、e)(单位：℃)

4 总结与讨论

(1)对于晴雨预报准确率，频率匹配法和阈值法在绝大多数预报时效对其均有明显提高，频率匹配法最大改进幅度可达20%以上。对于相对误差，频率匹配法的改进效果微小，经过阈值法二次订正后，空报现象有较显著的改进。对于1 h降雨量大于等于20 mm的短时强降水，经过频率匹配法订正后的TS评分有明显提高。频率匹配法订正效果与订正前预报的优劣有一定关系，而阈值法没有明显联系。对2018年“安比”台风事件预报的检验分析表明，除具有以上改进效果外，从天津降水最强时段的检验来看，频率匹配法提高了降水主体形态和量级的预报水平，阈值法将空报站预报正确且没有过度订正。

(2)对于2 m温度的ECWMF模式预报检验，其绝对误差随预报时效延长呈波动性增大，3—11月波动周期都是24 h左右，一个周期内的波峰、波谷位置在同一个季节内基本一致，不同季节之间有差异，夏季6月与7、8月差别较大，6月绝对误差范围和4、5月一致。秋季绝对误差曲线的波峰、波谷相较春、夏季更平缓。几乎在任何预报时效内都是3月绝对误差最大。通过应用Kalman滤波型的递减平均误差统计降尺度技术后，绝对误差都有不同程度的减小，春、秋季的绝对误差减小较明显，3月减小最大，6月几乎没有减小。总体上，订正后的绝对误差曲线仍具有周期性波动，波峰、波谷位置也与订正前基本一致，且绝对误差越大，订正幅度越大。个例分析也表明，订正后保留了温度预报的空间分布准确性，且绝对误差有明显下降。

上述研究结果虽然表明统计降尺度对降水和温度预报的订正效果较好，但是还有一些不足。例如，数据是逐小时数据，是对ECWMF细网格插值处理过的，由于降水具有不连续性，该插值方法是否最优还需进一步研究，并且对于不同地区，插值方法也需进行最优选取试验。另外，选取预报时效前一个月的时间段作为训练期，但是对于1 h累计降水，该训练期能不能非常准确地代表预报时效内降水频率分布还需要进一步研究，对于降水频率更高、强度更强的江南、华南和西南等地区，训练期更短、更接近预报时效可能代表性更强。