基于主成分分析的模糊频繁项集合挖掘方法

2022-03-15耿立校李恒昱刘丽莎

计算机仿真 2022年2期

耿立校，李恒昱，刘丽莎

(河北工业大学，天津 300401)

1 引言

模糊频繁项集合的挖掘是数据挖掘的关键步骤[1]，但通常情况下频繁项集合的数量较多，导致挖掘过程难度较大。针对数据中最大模糊频繁项集合中含有频繁项的特点，对模糊频繁项集合挖掘展开研究[2，3]。

文献[4]提出基于高效改进的模糊频繁项集合挖掘方法。该方法首先扫描数据库，构建存储项集关系的"投影"数据架构，提取出频繁1-项集和频繁2-项集，其次构建高阶项集的位置索引表，在跨越式搜索和连接的基础上找出模糊频繁项集合，实现模糊频繁项集合挖掘。但是由于该方法在模糊频繁项集合挖掘前没有对数据进行预处理，无法减少数据变量中的项，导致冗余数据的计算量过大，进而加大了方法运行内存。文献[5]提出基于DiffNodeset结构的模糊频繁项集合挖掘方法。该方法运用数据结构DiffNodeset求出支持度，并利用线性连接方法来降低连接的复杂度，减少无效计算量，其次在集合枚举树搜索空间的基础上利用优化剪枝策略减小搜索空间范围，最后中和超集检测技术提取模糊频繁项集合，实现模糊频繁项集合挖掘，该方法未利用主成分分析法对数据进行降维，而是直接对数据重新运算，只能在原始信息素排序表的基础上进行挖掘，该方法的挖掘计算量过大。文献[6]提出基于AO算法的模糊频繁项集合挖掘方法，该方法在滑动窗口思想的基础上对模糊频繁项集合分块挖掘，当满窗口有模糊频繁项集合进入时，利用区域插入的方式获取全新模糊频繁项集合，并求解支持度，同时结合超集检测，保证在最高效率下挖掘出模糊频繁项集合，实现模糊频繁项集合挖掘，该方法没有对模糊频繁项集合进行间隔约束处理而是直接挖掘模糊频繁项集合，导致散乱数据不能保持平衡，数据散乱程度过高，该方法的准确率、召回率和F1值均均不够理想。

为解决上述方法中存在的问题，引入主成分分析法，优化间隔约束条件下的模糊频繁项集合挖掘方法。通过实验验证了所提方法具有一定应用优势，为相关领域的研究提供可靠依据。

2 模糊频繁项集合预处理

2.1 修补模糊频繁缺损数据

经过标准化处理后的模糊频繁数据可相互对比，进而排除量纲带来的影响[7]，假设标准化处理后的模糊频繁项集合为X，X是由n个自身带有s维模糊频繁项数据的向量X1，X2，…，Xn组成，其中向量Xj=(x1j，x2j，…，xsj)T∈Rs，j=1，2，…，n，xi0j0是模糊频繁项的缺损数据，即需要修补的模糊频繁项数据。

假设向量Xj中的行向量为bi(i=1，…，s)，列向量为aj(j=1，…，n)，则模糊频繁项集合X的矩阵表达式为

(1)

将模糊频繁项集合X中的缺损数据xi0j0所在的第i0行进行消除，获取全新数据A，其矩阵表达式为

(2)

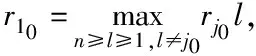
(3)

(4)

根据上述算法的逆过程将标准化数据还原成带有量纲的数据，最终输出的数据就是标准化后的完整数据。

2.2 基于主成分分析法的数据降维

主成分分析法是数据降维的重要手段之一，可提高数据挖掘效率，与其它降维手段相比，主成分分析法的降维力度最强[8]，该方法将修补后的完整模糊频繁项数据进行数值化处理，并按照数据类型将模糊频繁项数据划分成多个子数据集，并逐一进行降维，保证最大程度地排除数据中的冗余特征，其大致过程为：

①构建观测矩阵

假设数据中含有m个变量，对所有变量进行n次观测后每个子数据中都会生成n条样本数据，进而生成的观测数据矩阵表达式为

(5)

式中，xij表示分割后的子数据集，m表示模糊频繁项数据矩阵的行，即矩阵的每一行均是数据进行数值化后的一个样本模糊频繁项数据，n表示模糊频繁项数据矩阵的列，即划分后的子数据内的主成分样本个数。

②数据中心标准化

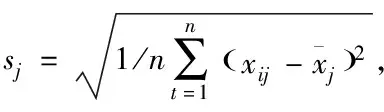
(6)

③求解样本数据相关矩阵R

④特征分解矩阵R，获取R=U∧UT

1)计算样本相关矩阵R的特征值

经计算发现矩阵R中含有m个特征值，将所有特征值自大到小的顺序进行排列后得到λ1≥λ2≥…≥λm≥0，进而求出所有主成分的贡献率，从中选取贡献率在85%以上的成分，并在这些成分中筛选出符合特征值小于1的前p主成分，筛选后的成分记为主成分分析结果，则主成分贡献率公式为

Cj=λj/(λ1+λ2+…+λm)

(7)

利用式(10)即可计算出每个主成分的贡献率，即每种成分可提供的信息量，Cj越大说明成分中信息量越多，且每个成分各自独立存在，即不存在信息重复的情况，因此提取满足上式两个要求的特征值即可。

2)计算特征向量

根据特征值的排序运算出对应的特征向量eig1，eig2，…，eigm，这些特征向量属于单位向量，即|eigi|=1，且特征向量两两相交，即eigi⊥eigj。

3)构建主成分载荷矩阵

根据贡献率最高的前p个主成分生成主成分载荷阵Um×p=(eig1，eig2，…，eigp)，则此矩阵就是主成分分析的最终结果，其中，m是特征向量的个数。

⑤将原始变量转换为主成分变量即可实现特征降维，即最大程度减少模糊频繁项数据数量，其表达式为

(8)

式中，ηi表示转化后的主成分变量，其中i=1，2，…，p，ξj表示原始变量，且j=1，2，…，m。

2.3 间隔约束最大模糊频繁项目集

在实际挖掘过程中，有项约束是最常用的约束条件[9]，假设项目约束条件是B，且B为I内的布尔代表公式，I是由多个不同的模糊频繁项目构成的集合，将约束条件B转换成析取范式(DNF)，即B1∨B2∨B3∨…∨Bk形式，在DNF形式下的约束条件集合为B={B1，B2，B3，…，BK}，且每个Bi表示b1∧b2∧b3∧…∧b1，其中bj∈I，假设T是模糊频繁项目集合的一个交易数据库，已知布尔表达式B，则可将间隔约束条件下的模糊频繁项目集合挖掘问题转化成提取符合约束条件B的模糊频繁项目集合问题，且挖掘过程中还需保证挖掘结果的支持度大于等于固定的最小支持度阈值[10]。

3 模糊频繁项目集合挖掘

模糊频繁项集合中的数据虽隶属于同一数据库，但实际上数据分散在各个场地，将模糊频繁项数据利用传统方法进行分类难度较大，而蚁群优化系统具有记忆性、自主性、反应性、容错性、社会性、移动性以及适应性等优点[11]，基于以上优点可将此方法应用于数据挖掘中，同时可建立出一条又一条互不依赖的规则，按照历史错误更新经验，逐一计算得出最优解，即生成ACO分布式分类算法，此算法首先将数据进行初始化处理，获取所有挖掘通道的相关信息，并计算出数据相关函数，进而生成一条有规则又互不依赖的数据挖掘通道，其次修剪规则从而修改蚁群爬行路径的信息，最终在所有规则中提取出一条质量最优的规则，根据此规则挖掘出模糊频繁项数据。

综上所述可知在建立规则前必须提前求解规则内所需的条件项，并根据规则自身的条件项得出可能执行此任务的可能性P，其表达式为

Pij(t)=Rij(t)2/θ+Rij(t)2

(9)

利用蚁群算法建立出规则后的信息素总数表达式为

τij(t)=τij(t-1)·(1-1/(1+Q))

+(1-ρ)·τij(t-1)

(10)

式中，ρ表示信息素可能损失的概率，Q表示根据蚁群算法建立的规则质量。

参数ρ可直接反映出蚁群算法在爬行过程中信息的损失速度，因此参数ρ越大，此路径中的信息损失速度越快。在对一个训练集进行多次蚁群算法后即可获取多条数据分类规则，利用Q选取出其中质量最优的规则，则Q的表达式为

Q=(TruePos/FalseNeg+TruePos)×

(TrueNeg/FalsePos+TrueNeg)

(11)

式中，TruePos代表规则路径中满足规则的条件项，且此条件项的数量和预测出规则类型数量一致，FalsePos代表规则路径中满足规则的条件项，但此条件项的数量和预测出规则类型数量不相同，FalseNeg代表规则路径中不符合规则的条件项，但此条件项的数量和预测出规则类型数量一致，TeueNeg代表规则路径中不符合规则的条件项，且此条件项的数量和预测出规则类型数量不相同。

根据信息素和启发函数值选出最优规则路径后将条件项添加到规则路径中，保证数据分类准确率最高的同时还可简化分类规则[12]，将数据进行最优分类，实现模糊频繁项集合挖掘。

4 实验与结果

为验证所提方法的整体有效性，对间隔约束条件下的模糊频繁项集合挖掘方法、文献[4]方法和文献[5]方法进行运行内存和挖掘有效性的测试。

4.1 运行内存大小测试

根据图1可看出随着最小支持度的增加，三种挖掘方法的运行内存均有所下降，进而提高系统的流畅程度，但所提方法的运行内存最大为65M，随着最小支持度的增加其运行内存一直在下降，因此所提方法的系统最流畅，其它两种方法的运行内存过于依赖系统支持度，在支持度过小的情况下两种方法的最大运行内存分别为105M和140M，导致文献[4]方法和文献[5]方法的系统比较卡顿，而所提方法可一直保证系统流畅是因为在进行模糊频繁项集合挖掘前对数据进行了预处理，数据变量中的项明显下降，排除大量冗余数据，保证了系统的流畅程度，降低运行内存使用率。

图1 不同方法的运行内存使用情况

4.2 挖掘有效性测试

随机选取了六组训练数据，比较三种方法处理后的数据精确率、召回程度以及F1值，模糊频繁项集合中的信息素比较散乱，对这种数据进行挖掘有较大的难度，难以保证其挖掘有效性，如图2所示，文献[4]方法在挖掘时只能加大计算量进而提高准确率、召回率和F1值，文献[5]方法没有做任何处理，导致其挖掘有效性十分低下，而所提方法经过对数据的间隔约束处理后进行数据挖掘，相当于将信息素进行一个平衡处理，使得数据的散乱程度有所改善，因此无论是所提方法的准确率、召回率还是F1值，它都是三种方法中最优的方法，验证了所提方法的有效性。