改进扩散式子带自适应滤波算法仿真

李晶晶，孙 贞，满永恒

(大连市气象装备保障中心，辽宁 大连 116001)

1 引言

分布式估计是从分布式网络和传感器采集的数据中获取感兴趣参数的一种估计方法[1]，在无线传感器网络、目标定位、环境监测、医学等领域得到了广泛应用[2-5]。分布式网络中根据节点通信方式的不同主要分为递增式策略、扩散式策略和概率扩散式策略[6]。扩散式策略因其具有较好的稳健性而被广泛采用。传统的扩散式最小均方(Diffusion Least Mean Square，DLMS)算法[7]是在LMS算法的基础上发展起来的一种分布式估计方法，但对于有色输入信号，其收敛速度会急剧下降。扩散式仿射投影算法(Diffusion Affine Projection Algorithm，DAPA)[8]利用数据重用改善有色输入信号的收敛性，但其计算复杂度较高。

扩散式子带自适应滤波(diffusion subband adaptive filtering，DSAF)算法及其改进的算法[9-16]很好地解决上述问题并且具有较低的计算量。该类算法通过子带自适应滤波器的滤波器组分割有色输入信号降低信号相关度从而加快算法的收敛速度，并且子带自适应滤波器中加入降采样环节，因而DSAF算法的计算复杂度接近于DLMS算法。

上述算法都是基于高斯假设下进行推导而来。然而，现实生活中存在大量的非高斯噪声，其中包含自然环境下的雷电噪声、电磁波干扰噪声、水声噪声和人为噪声等。实际工程中的非高斯噪声脉冲特性和重尾特性严重影响着基于l2范数优化准则的分布式自适应滤波算法性能。基于熵理论提出的扩散式最小误差熵算法(Diffusion minimum error entropy，DMEE)算法和扩散式最大相关熵(Diffusion Maximum Correntropy Criterion，DMCC)算法具有良好的鲁棒性[17]。但是在有色输入条件下，上述算法的收敛性能变差。扩散式符号子带自适应滤波(Diffusion Sign Subband Adaptive Filtering，DSSAF)算法[18]是将符号函数与子带自适应滤波器相结合的一种分布式算法，该算法不仅抑制非高斯噪声，而且对有色输入信号具有良好的收敛特性。单独加权因子的扩散式符号子带自适应滤波(Individual Weighting Factors DSSAF，IWF-DSSAF)算法[19]是在DSSAF算法基础上改进的，其原理是将DSSAF算法中的每个子带的同一加权因子替换为单独的加权因子，从而获得更快的收敛速度。

此外，声学回声信道、数字电视传输信道、大型视频会议和水下通信系统等实际应用场合中待估计系统常呈现出稀疏特性[20，21]。这意味着大多数信道系数的值为零或非常小，其中只有小部分系数具有显著的幅度，充分利用该特性可以提高算法的收敛速度，减少算法计算复杂度。为此，研究学者提出了很多稀疏系统的算法。其中最常见的一种方法是使用自适应比例矩阵技术[22]来改善算法的收敛速度，该技术的主要思想是比例分配矩阵为每个系数分配不同的增益，较大的系数获得较大的增益以提供较大的步长，反之亦然。DSSAF算法与自适应比例矩阵技术结合提出了IPDSSAF(Improved Proportionate Diffusion Sign Subband Adaptive Filtering，IPDSSAF)算法[23]，该算法在稀疏系统下有着良好的收敛速度。另外，IWF-DSSAF算法结合自适应比例矩阵思想提出了单独加权因子扩散式符号子带自适应滤波(Individual Weighting Factors IPDSSAF，IWF-IPDSSAF)算法[19]，该算法相比于IPDSSAF算法有更好的收敛性能。

2 算法

2.1 DSAF算法

由N个节点构成的无线传感器网络中节点n的期望信号dn(l)由线性模型得到

(1)

其中，un(l)=[un(l)，un(l-1)，…，un(l-M+1)]T为节点n的输入信号，w0是长度为M的待估计向量，ηn(l)为测量噪声，T表示向量的转置，l表示抽样前的时间序列。图1为分布式子带自适应滤波算法的原理框图。

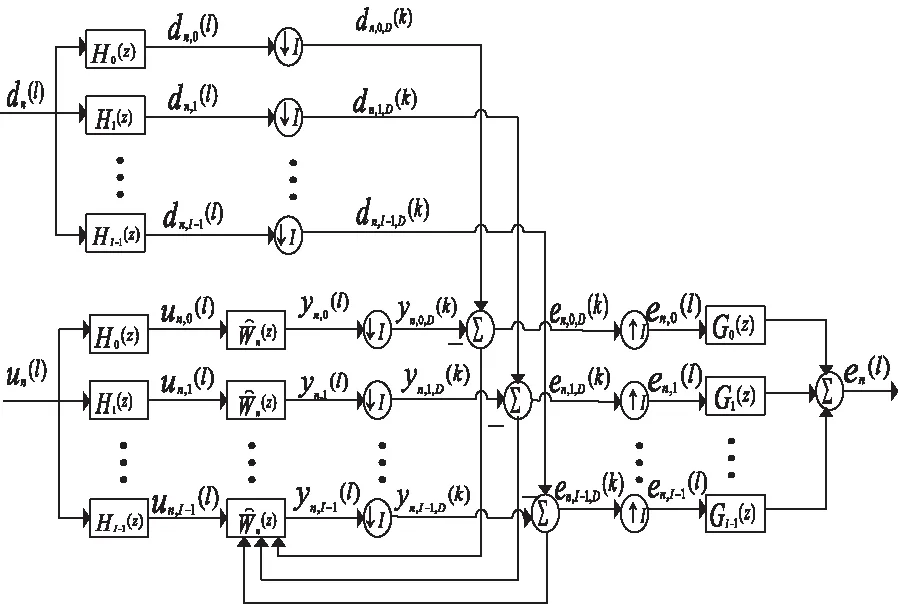
图1 分布式子带自适应滤波器的结构

图1中↑和↓分别表示插入和抽取，un(l)和dn(l)经过分析滤波器Hi(z)分割成子带输入信号un，i(l)和子带期望信号dn，i(l)，其中，i=0，1，…，I-1，I表示子带数目。

un，i(l)经过子带自适应滤波器n(z)生成子带输出信号yn，i(l)，子带期望信号dn，i(l)和子带输出信号yn，i(l)进行抽取，得到抽取后的子带期望信号dn，i，D(k)和子带输出信号yn，i，D(k)，两者相减之后得到子带误差信号en，i，D(k)来调整自适应滤波器参数来达到最佳的滤波效果。最后，子带误差信号en，i，D(k)经过综合滤波器Gi(z)得到全带误差信号en(l)。其中，D为抽取因子，k表示抽样后的时间序列且l=kI。

在分布式估计中，节点n的子带输入向量和节点n的第i个子带的输出向量分别为

un，i(k)=[un，i(kI)，un，i(kI-1)，…，un，i(kI-M+1)]T

(2)

(3)

其中，wn(k-1)表示节点n对w0的估计值。

DSAF算法的更新公式为

(4)

其中，en，i，D(k)可以写成：

(5)

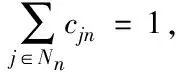
特别地，在分布式自适应滤波算法中，根据自适应步骤和联合步骤的先后顺序可分为ATC型(Adapt-and-Combine)和CTA型(Combine-and-Adapt)。一般情况下ATC方案相比于CTA方案更快速地遍历网络中的节点，具有高效性[24]。因此本文算法是基于ATC型展开讨论的。

2.2 DSSAF算法和IWF-DSSAF算法

1)DSSAF算法

DSSAF算法的更新公式可由如下约束最优化获得

(6)

其中，节点n的子带期望向量和子带输入矩阵分别定义为：

dn(k)=[dn，0，D(k)，dn，1，D(k)，…，dn，I-1，D(k)]T

(7)

Un(k)=[un，0(k)，un，1(k)，…，un，I-1(k)]

(8)

利用拉格朗日乘子的方法来解决上述约束优化问题，DSSAF算法的更新公式为

(9)

其中，ε表示正则化参数，sgn 表示符号函数。节点n的子带误差向量en，D(k)定义为

=[en，0，D(k)，en，1，D(k)，…，en，I-1，D(k)]T

(10)

DSSAF算法中的符号函数虽然能够抑制非高斯噪声干扰，但是DSSAF算法的所有子带都通过共同的加权因子互连，这直接影响其收敛性能。因此，下面给出了IWF-DSSAF算法。

2)IWF-DSSAF算法

IWF-DSSAF算法是在DSSAF算法基础上加以改进的。DSSAF算法中每个子带的同一加权因子替换为单独的加权因子而获得的IWF-DSSAF算法改善了收敛速度。其更新公式为

(11)

从(11)式可以看出，IWF-DSSAF算法中节点n的每个子带的单独加权因子与相应的子带输入信号方差平方根成反比，这意味着输入信号方差的平方根较小的子带具有较大的权重。因此，相比于DSSAF算法，IWF-DSSAF算法在收敛性能上有显著提高。

2.3 IPDSSAF算法和IWF-IPDSSAF算法

DSSAF算法和IWF-DSSAF算法在非高斯噪声干扰下具有良好的鲁棒性，但是并未考虑系统的稀疏特性。因此，将自适应比例矩阵技术引入到DSSAF算法和IWF-DSSAF算法中，得到的IPDSSAF算法和IWF-IPDSSAF算法能够适应信道的不同稀疏特性。

1)IPDSSAF算法更新公式为

(12)

2)IWF-IPDSSAF算法更新公式为：

(13)

其中，Gn(k)表示节点n是M×M的步长控制矩阵，其定义为

Gn(k)=diag[gn，1(k)，gn，2(k)，…gn，M(k)]

(14)

(15)

α是一个与系统稀疏度有关的参数，δ是一个正则化参数，防止分母为零。算法中引入步长控制矩阵，步长参数与滤波器系数成正比，算法迭代一次后，全部参数的成比例因子重新进行成比例分配，大系数获得大步长，小系数获得小步长，从而加快了算法的收敛速度。

与IWF-DSSAF算法类似，由于IWF-IPDSSAF算法有效地利用了单独子带自适应滤波的固有去相关特性，因此IWF-IPDSSAF算法比IPDSSAF算法具有更快的收敛速度。

3 仿真研究

3.1 仿真条件

在本文实验中，网络由20个节点组成，彼此链接按照Metropolis准则[24]形成，具体的网络拓扑结构图如2所示，区域范围为[0，1.2]×[0，1.2]。

图2 本文所采用的网络拓扑结构

为验证算法性能，本文将所有算法应用到系统辨识系统。待估计的稀疏系统脉冲响应如图3所示，它们的稀疏度分别为0.751和0.5946。

图3 不同稀疏度的稀疏信道

图4 输入信号和高斯白噪声方差

图5 各节点信噪比

图6 Pr=0.01(上)和Pr=0.1(下)的各节点信号干扰比

3.2 性能指标和参数设置

本实验采用网络均方误差(Network Mean Square Deviation，NMSD)作为算法收敛性能的衡量标准。

(16)

NMSD的值越小意味着自适应滤波器越逼近未知系统。为了更加方便比较不同算法之间的差异，学习曲线为30次独立仿真后使其取平均的结果。

3.3 仿真结果与分析

1)高斯噪声条件下的DLMS算法和DSAF算法性能比较

图6为Pr=0时有色信号作为输入的DLMS算法和DSAF算法的NMSD收敛曲线图。它们的步长参数分别为0.0003和0.81。

图5 DLMS算法和DSAF算法的性能比较

图6 Pr=0.01的非高斯噪声条件下白信号作为输入信号的各类算法的NMSD收敛曲线

在图5中，当有色信号作为输入且相关性较高时，DSAF算法的收敛速度和稳态误差明显优于DLMS算法。验证了子带分割有色信号降低信号相关性来加快算法的收敛速度。

2)Pr=0.01，白输入信号的各类算法性能比较

图6所示为Pr=0.01的非高斯噪声条件下白信号作为输入信号的DSAF算法、DSSAF算法、IWF-DSSAF算法、IPDSSAF算法和IWF-IPDSSAF算法的NMSD收敛曲线。它们的步长参数分别设置为0.5、0.14、0.07、0.02和0.08。

由图6可以看出非高斯噪声条件下，DSAF算法收敛以及稳态性能很差。将其它算法的收敛速度保持一致时，IPDSSAF算法和IWF-IPDSSAF算法的稳态误差优于DSSAF算法和IWF-DSSAF算法，这是因为自适应比例矩阵的优势增强了算法的收敛性能。DSSAF算法和IWF-DSSAF算法以及IPDSSAF算法、IWF-IPDSSAF算法稳态误差分别几乎相同，因为IWF-DSSAF算法和IWF-IPDSSAF算法分别是DSSAF算法和IPDSSAF算法的子带变体，而子带分割白信号在一般强度非高斯噪声干扰不起作用。

3)Pr=0.1，白输入信号的各类算法性能比较

图7所示为Pr=0.1的非高斯噪声条件下白信号作为输入信号的DSAF算法、DSSAF算法、IWF-DSSAF算法、IPDSSAF算法和IWF-IPDSSAF算法的NMSD收敛曲线。它们的步长参数分别设置为0.25、0.7、0.34、0.065和0.4。

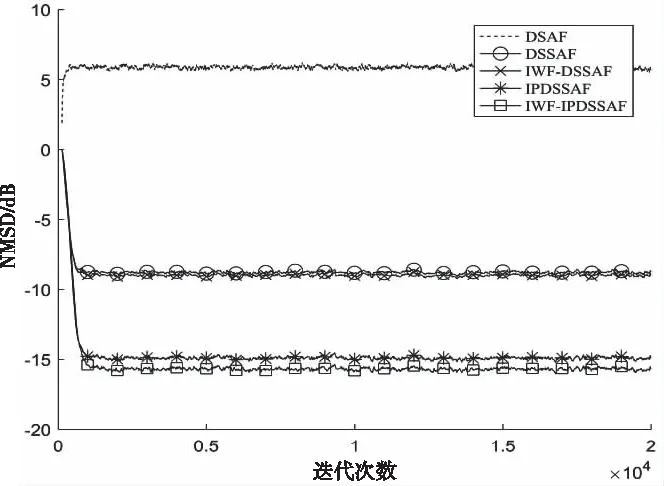
图7 Pr=0.1的非高斯噪声条件下白信号作为输入信号的各类算法的NMSD收敛曲线

相比于图6，其它条件不变，图7将Pr的值从0.01增大到0.1，DSAF算法已经完成失效。其它算法的收敛速度与稳态误差性能也变差。因此，伯努利脉冲噪声的概率密度大小直接影响算法的性能。

4)Pr=0.01，有色输入信号的各类算法性能比较

图8所示为Pr=0.01的非高斯噪声条件下有色信号作为输入信号的DSAF算法、DSSAF算法、IWF-DSSAF算法、IPDSSAF算法和IWF-IPDSSAF算法的NMSD收敛曲线。它们的步长参数分别设置为0.1、0.42、0.055、0.0158和0.3。

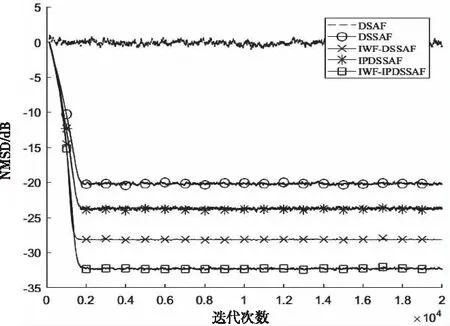
图8 Pr=0.01的非高斯噪声条件下有色信号作为输入信号的各类算法的NMSD收敛曲线

由图8可以看出，非高斯噪声干扰条件下，DSAF算法已知失效，其它四种算法仍然保持很好的收敛性能。由于自适应比例矩阵的优势，IPDSSAF算法和IWF-IPDSSAF算法收敛速度与稳态误差性能分别优于DSSAF算法和IWF-DSSAF算法。IWF-IPDSSAF算法的每个子带单独加权以及结合自适应比例矩阵技术使其性能优于其它所有算法。

5)Pr=0.1，有色信号输入的各类算法性能比较

图9所示为Pr=0.1的非高斯噪声条件下有色信号作为输入信号的DSAF算法、DSSAF算法、IWF-DSSAF算法、IPDSSAF算法和IWF-IPDSSAF算法的NMSD收敛曲线。它们的步长参数分别设置为0.1、0.25、0.06、0.021和0.25。

相比于图8，图9其它条件不变，将Pr的值从0.01增大到0.1。所有算法性能退化。IWF-IPDSSAF算法的收敛速度与稳态误差依旧优于其它所有算法。

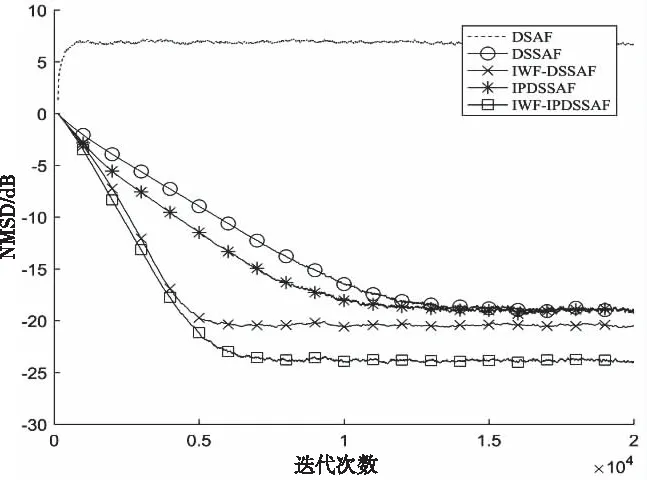
图9 Pr=0.1的非高斯噪声条件下有色信号作为输入信号的各类算法的NMSD收敛曲线

6)Pr=0.01，双信道下的各类算法性能比较

图10所示为Pr=0.01的非高斯噪声条件下有色信号作为输入信号的DSAF算法、DSSAF算法、IWF-DSSAF算法、IPDSSAF算法和IWF-IPDSSAF算法的跟踪曲线。迭代次数为20000时，信道的稀疏度从0.6689变为0.5946，各类算法依然保持良好的跟踪性能。

图10 Pr=0.01的非高斯噪声条件下有色信号作为输入信号的各类算法的跟踪性能

4 结论

本文首先研究了传统的扩散式子带自适应滤波(DSAF)算法，传统的DSAF算法利用子带技术分割相关信号加快了算法的收敛速度；其次，深入研究了非高斯噪声下稀疏系统的改进扩散式子带自适应滤波算法；最后，将DSAF算法以及改进的DSAF算法在不同脉冲性的非高斯噪声环境、稀疏信道下进行仿真。结果表明，改进的DSAF算法具有良好的稳健性和收敛性。