融合梅尔谱和循环残差的小样本音频分类模型

樊翔宇，张 聪，杨 柳

(1.武汉轻工大学数学与计算机学院，湖北 武汉 430040；2.香港科技大学计算机科学与工程系，香港 九龙 999077)

1 引言

随着隐私保护政策日益完善和个人隐私意识逐渐增强，音频分类领域有效样本数不断减少，在小样本场景下获得尽可能高的分类精度成为需要解决的问题。

区分音频信号的标准有频率、幅度、响度、音调等物理特征和熵值、过零率、频谱图等间接特征。虽然针对小样本音频信号分类的专门研究还不多，但近年来先后有学者基于上述特征做过与音频信号分类相关的工作。2019年Roneel等[1]融合耳蜗图和卷积神经网络提出了一种声学事件检测方法，同年孙慧芳等[2]结合过零率和频谱等音频特征设计了一种用于人声和乐声两种信号分类的算法。次年Kun-Ching Wang等[3]又使用熵和语音端点检测构建了另一种语音/音乐分类算法，McLoughlin等[4]则以时域特征和频域特征为基础建立了检测噪声的音频处理模型。这些研究证明音频信号具有可分性，且在处理人声、乐声、噪声等特殊音频信号时有较好的效果，但适用范围有局限。

小样本理论源自Gosset[5]，在物理学、生物学等领域的细分方向已有研究和应用[6，7]。在音频分类问题中，当一个标签下所属的有效样本数少于50时，可视为小样本场景。对小样本下样本不足产生的一系列问题，有学者尝试从自身所在领域寻找解决方法，Alexander Buslaev等[8]在图像领域提出数据增强扩展图像数据的规模，机器学习领域则应用正则化、元学习等方法减轻小样本下的过拟合[9，10]。然而音频是时频信号，简单应用旋转、折叠等图像增强方式易造成信号失真，元学习则与杨强等[11]提出的迁移学习理论有一定相似度，可作为迁移学习理论的前置理论，此外何凯明等[12]论文中的残差网络在结构上具备用于小样本音频分类建模的可行性。

梅尔滤波(Mel Filter，MF)的掩蔽效应能较好的将音频信号关键特征转换为频谱图，音频信号图像化后更适合神经网络进一步处理，但在小样本下朴素梅尔滤波还需增强。残差网络在图像领域应用广泛，有效性经过充分验证，但只考虑了单向跨层，在小样本下尚有改进空间。因此以自适应梅尔滤波(Adaptive Mel Filter，AMF)算法对朴素梅尔滤波过程进行增强、以双向跨层的循环残差结构建立循环残差网络频谱分类器(Recurrent Residual Network Spectrum Classifier，RRNSC)，并在分类器中加入模拟正则化约束弱化小样本下的过拟合，借助迁移和微调[13]融合二者构建AMF-RRNSC小样本音频信号分类模型。该模型在小样本仿真中显示出比主流模型更高的分类精度，具备一定的参考和应用价值。

2 高区分度频谱图提取

2.1 朴素梅尔滤波

人类感知音频需经人耳提取特征，有研究表明并非所有音频信号都会在人耳得到同等程度的响应[14]，当响度不同的声音同时到达人耳时，人耳易对响度较高的信号给予更多关注，而忽视响度较低的信号，这被称为人耳的掩蔽效应。在吸收人耳掩蔽效应的基础上，Davis等[15]提出朴素梅尔滤波音频频谱提取方法，包括预加重、分帧、加窗、快速傅里叶变换、滤波、对每个滤波器计算对数能量等处理过程。

预加重通过高通量滤波器截频输入信号，弱化低频干扰。常用滤波函数形如式(1)，t为时间序列的刻度，N(t)是经过高通量滤波后t时刻的幅度，S(t)和S(t-1)分别表征t时刻和上一时刻原始音频信号的时域幅度，u为滤波系数，朴素滤波系数为0.9。

N(t)=S(t)-u*S(t-1)

(1)

分帧是将需处理的采样点转换为聚合后的帧，降低处理过程的时空复杂度，朴素梅尔滤波过程常将每128或256个采样点聚合为一帧。

加窗可避免帧间干扰，通过窗间重叠增强帧间连续性，过程可总结为式(2)，T(n)指要加窗的帧，W(n)是作用于这一帧的窗函数，φ是区分窗函数的系数。常用的有矩形窗、三角窗，系数分别为0、0.5。

T(f)=T(n)*W(n)

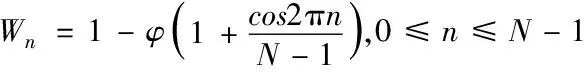
(2)

时域信号不含频域范围的特征，如果将时域上的波形曲线看作一个周期与时长相等的周期函数，根据傅里叶提出的相关理论[16]，该函数可表示为无穷多个正弦函数的叠加，因此加窗后做快速傅里叶变换可得时域信号在频域上的特征。

滤波通过梅尔倒谱系数(MFCC)实现，是将线性频率拟合为契合人类听觉系统的非线性频率的关键。求解过程同式(3)，f是音频的原始频率。

Mel(f)=2595*lg(1+f/700)

(3)

对数能量可定义为(4)，其中Xm是每帧音频内所有采样点能量的平方和，F(n，k)是与滤波器有关的定义，N是滤波器的个数，朴素滤波器个数为24。

(4)

2.2 自适应梅尔滤波

朴素梅尔滤波过程使用固定参数(如采样率、梅尔滤波器组数、窗长等)，每个步骤难以局部最优，多个非局部最优累加导致最终结果无法全局最优。自适应梅尔滤波算法从滤波参数考虑，自局部向整体优化获得高区分度频谱图，图1是采样频率、窗长和滤波器个数不同时得到的梅尔滤波曲线，参数不同时曲率和值域存在较大差异，不同曲线得到的频谱图不尽相同，这是自适应梅尔滤波算法的理论基础。

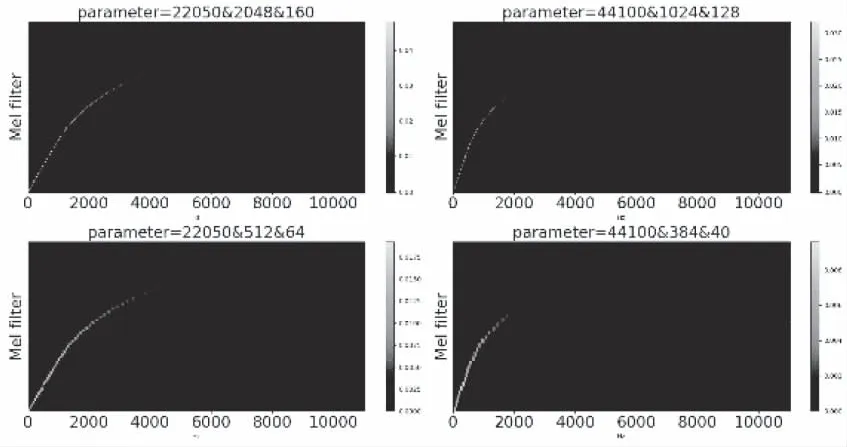
图1 不同参数下的梅尔滤波器组

为增强朴素梅尔滤波过程，提取区分度更高的频谱图，初次提取时算法根据朴素梅尔滤波过程为提取参数设置初值，同时初始化迭代阈值N，并生成堆栈结构记录分类器反馈和当前参数。初次提取完成后将特征送入RRNSC分类器，分类完成后将验证集上得到的分类精度反向传播至频谱提取层。提取层向堆栈写入当前迭代次数n、分类精度和参数等关键记录，遍历堆栈并根据已有最佳精度及对应的参数以式(5)调整第n+1次迭代时的参数，式中n是当前迭代步数，d是调整率，Cn是第n次迭代时分类器反馈的分类精度，Dn是第n次迭代时使用的参数值，n为0时取朴素梅尔滤波过程的参数为初值。当n等于N时迭代停止，遍历堆栈并以堆栈现有最佳参数生成适用于该类音频信号的AMF参数。

(5)

AMF算法对朴素梅尔滤波的增强可总结为式(6)，与朴素梅尔滤波过程涉及的公式比较可知AMF过程多出参数动态调整，调整函数D(x)同式(5)，x是需动态调整的参数。如果将频谱图的区分度定义为[0，1]，设朴素梅尔滤波过程得到的区分度上限为β，β∈[0，1]，则由图2算法过程易知在最坏情况下AMF提取的区分度将不低于β。

N(t)=S(t)-Du*S(t-1)

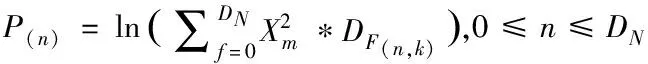
(6)

综合以上论述，自适应梅尔滤波算法实现局部最优，得到高区分度频谱的过程可由图2表示。

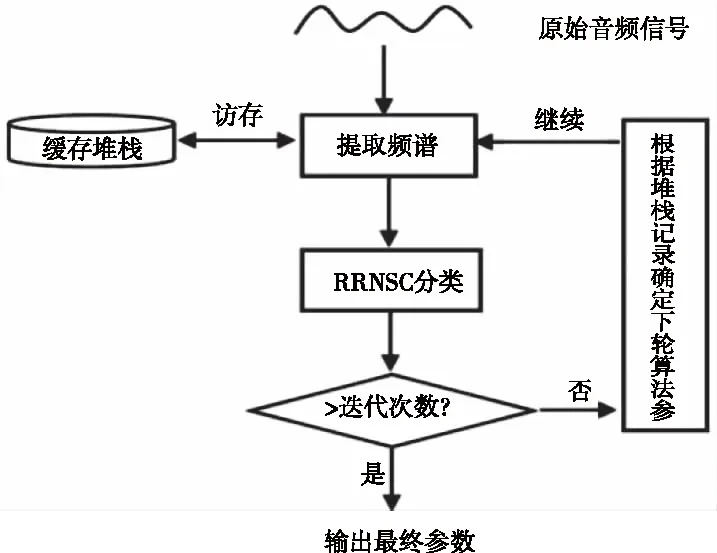
图2 AMF算法过程

图3-图4是使用图像直方图对music speech数据集中ballad音频片段经AMF算法和朴素梅尔滤波过程分别得到的频谱的直观描述，bin为256。

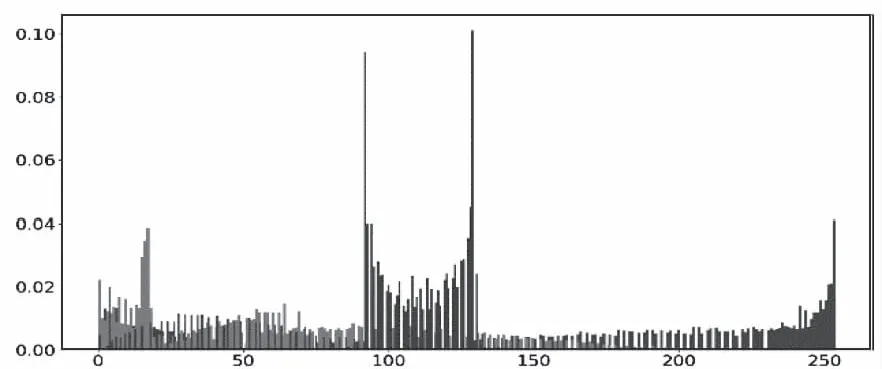
图3 AMF算法得到的直方图

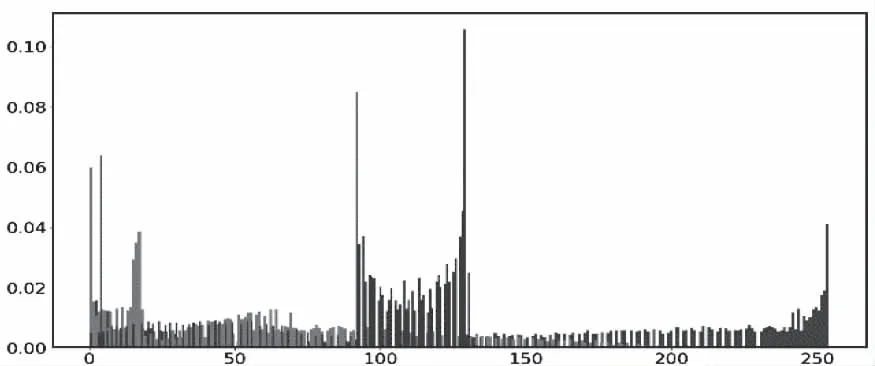
图4 朴素梅尔滤波得到的直方图

通过定量计算直方图相关系数可知相似度为81.70%，该数据集中所有音频片段总相似度为73.12%，计算公式如式(7)，其中N是直方图中bin的个数。

(7)

上述结果说明AMF算法提取的频谱区分度与朴素梅尔滤波存在较大不同，证明算法的理论基础是正确的。

3 小样本频谱分类

3.1 深度神经网络的性能退化

如果样本数量足够，神经网络的表现会随着模型复杂度(层数和权重数量)的提升和训练步数的增加而提升。但实际应用中样本规模有限时更深层卷积神经网络(Convolutional Neural Network，CNN)的性能却随着训练步数的增加出现退化，当训练步数达到阈值后，更深层网络性能反而差于较浅层网络，使网络性能遇到瓶颈。图5在ESC-50数据集上验证了CNN中性能退化问题的存在，随着epoch的增加，24层CNN的分类精度反而低于10层CNN，由图可知此时的阈值在40至60之间。

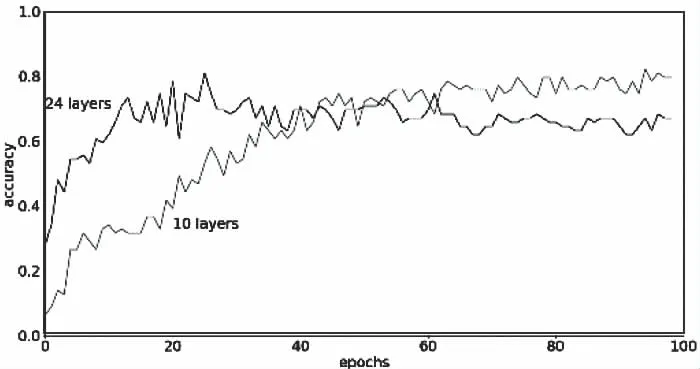
图5 10/24层CNN在ESC-50上的分类精度趋势

3.2 循环残差网络

分析常规CNN的结构可知，其内部都是顺序连接，数据必须先经过第k层才能经过第k+1层，因此每个输入样本都会均衡影响所有权重并受所有权重的影响，这是性能退化出现的原因之一。残差在网络的不同层建立跨层连接，样本既可逐层传递，也可跨越不同层次传递，从而避免样本和权重间无差别的影响。摘要中提出的循环残差将普通残差结构中的单向跨层传递改进为双向跨层传递，以得到小样本下更好的分类性能，图6是跨两层的循环残差结构示意，每个双向连接间的跨层数可依需求设定，不局限于2层。

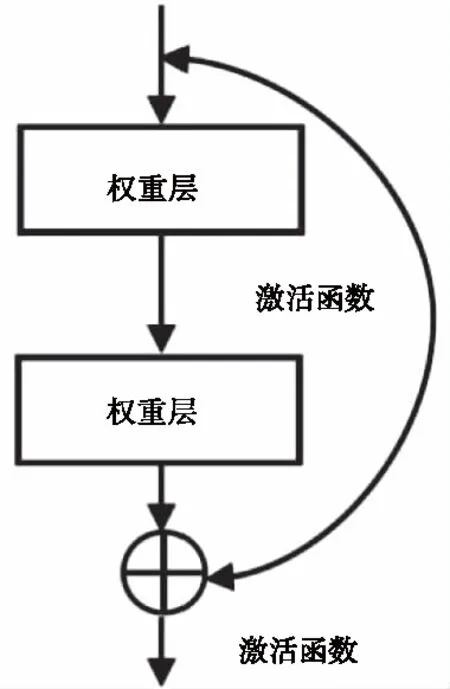
图6 循环残差结构图

RRNSC以循环残差为基础结构构建，共有23608202个参数，51层深度，并迁移image net在Res net 50残差网络上的权重初始化所有参数。迁移是指将网络在数据集A得到的参数作为在数据集B训练时的起始[17]，使网络继承已在A上得到的经验。image net是一个千万级样本的大型公开图像数据集[18]，量纲可与RRNSC的参数相匹配，且已有多个研究机构使用image net在Res net 50上做过训练并发布了可信的权重，权值不存在一致性问题，迁移可节省训练时间和计算资源消耗，加快建模速度。

RRNSC的主要结构见表1，其中输出层的D(dataset)意为根据数据集动态调整频谱类别量，Average Pooling是全局平均池化层，作用与正则化类似，避免小样本下的过拟合。

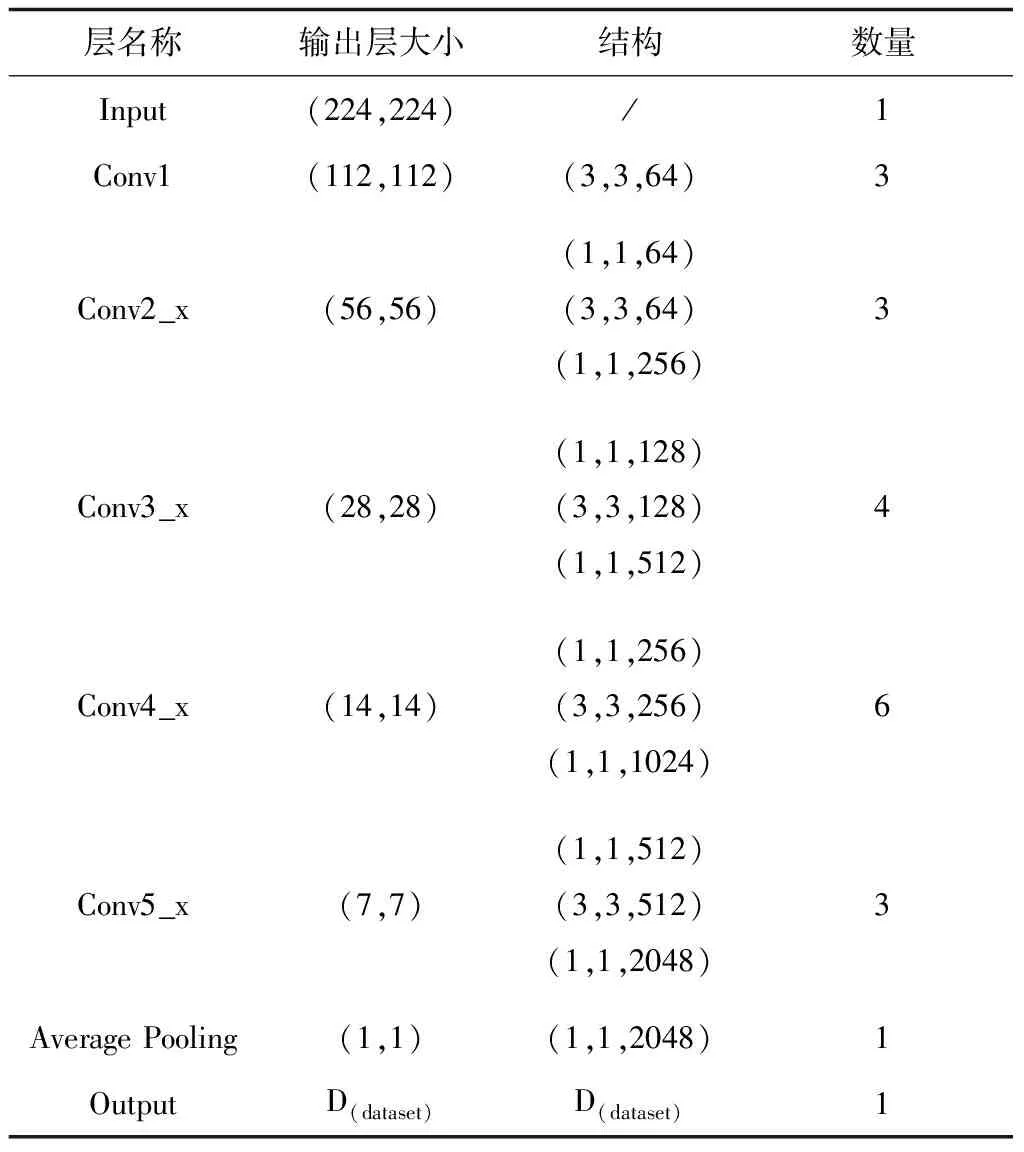
表1 RRNSC主要结构

分类器内部使用Adam算法优化模型参数。Adam是模型优化方向最新的研究成果之一，算法基于梯度下降思想自动更新与当前迭代相适应的权重[19]。网络输出层由softmax函数计算属于某一类别的概率，计算方法见式(8)，分子ci是待分类目标属于这一类别的概率，分母是属于所有类别的总和概率。

(8)

得到softmax的输出后，使用交叉熵算法(Cross Entropy)计算训练损失，计算过程如式(9)，P和Q分别是预测集和正确集。引入交叉熵算法而不使用均方误差(Mean Squared Error，MSE)等算法的原因是在分类问题中，交叉熵算法可以得到单调的损失函数[20]，利于Adam反向优化迭代权重值，而MSE等算法往往得到的是非单调的损失函数，对优化模型参数不利。

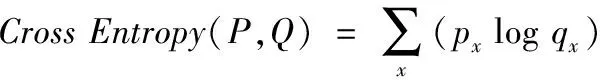
px∈P，qx∈Q

(9)

4 AMF-RRNSC模型

AMF算法误差传播和梯度下降的快慢及最终输出频谱的区分度均受后置分类模块的影响，因此在AMF-RRNSC模型中AMF算法和RRNSC是两个不可分割的部分。只有将AMF算法作为前置提取层，RRNSC作为后置分类层，才可构建出完整的AMF-RRNSC音频分类模型。

模型结构见图7，每轮分类结果存在反向传播次数上限，在AMF-RRNSC模型中提供100作为默认值，也可根据具体任务自定义该值。

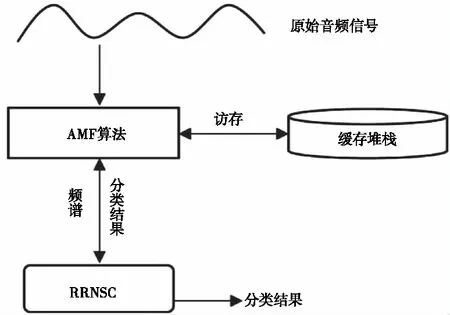
图7 AMF-RRNSC模型结构

5 实验

根据Rishabh N.Tak等人论文[21]构建具有10层深度不含残差的常规卷积神经网络(10 layers CNN，结构见表2)，引入Karen Simonyan等人论文[22]中的VGG16网络并结合朴素梅尔滤波过程构建MF-VGG16，引入Sailor等人论文[23]中的CRBM模型。其中10 layers CNN和CRBM对音频信号本身做分类，MF-VGG16对朴素梅尔滤波提取的频谱做分类，因此MF-VGG16可辅助验证AMF和RRNSC。

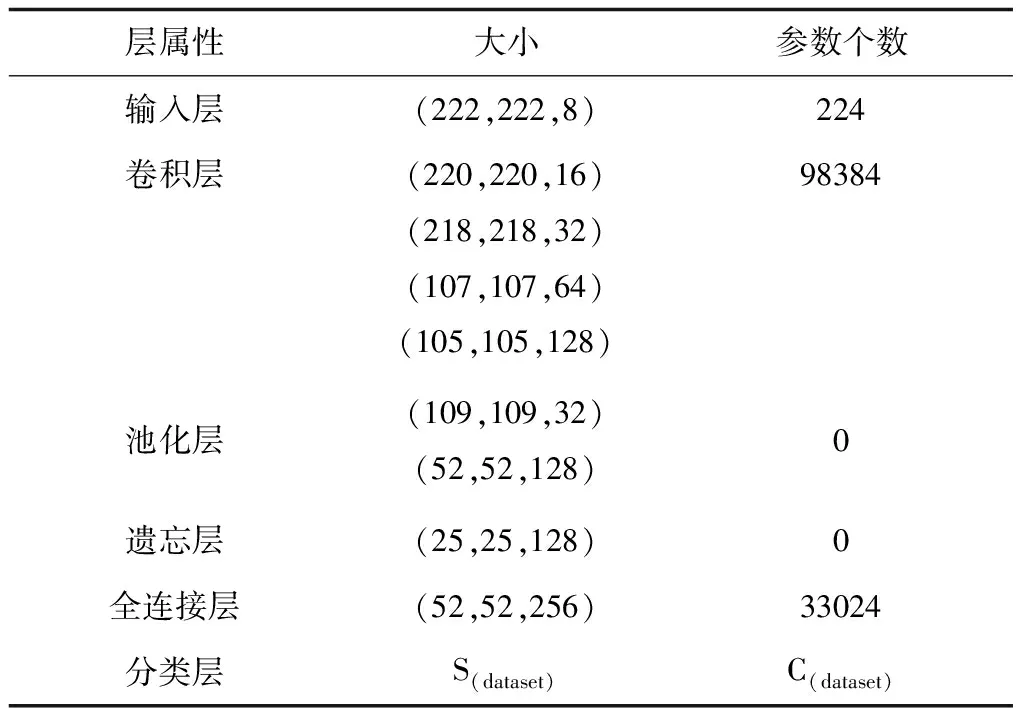
表2 10 layers CNN各层次

使用ESC-50、music speech、Free ST Chinese Mandarin Corpus(FSCMC)作为基本数据集分别模拟小样本等时长多分类、小样本等时长二分类、小样本不等时长多分类。ESC-50含50种环境声音，每种40个时长约5秒的样本[24]，是等时长多分类数据集。music speech有乐声(music)和人声(speech)2种类别，每种64个时长约30秒的样本，是等时长二分类数据集。FSCMC是北京冲浪科技发布的开源中文音频数据集，根据实验需求选择该数据集的20170001＿1版本，包括855个读者(性别比1：1)使用中文朗读的102600段不等时长语音片段，每个读者对应的样本都大于40，因不同读者的音色、音调、响度等均不同，所以这些片段可分为855个类别。以上数据集中的样本都是wav无损音频格式，可尽量避免其它因素对实验结果的影响。为满足小样本约束，实验前music speech数据集和FSCMC数据集中的每个类别均随机选取40个片段，选取完成后实验时不再重复选取，保证各实验所用样本无差异。为形成充分对照，混合ESC-50和music speech两个数据集生成含52个类别，每个类别40个样本的第四个小样本数据集ESC-50&music speech加入实验。

所有实验均将数据集随机划分为80%训练集和20%测试集并采用相同的随机数种子，实验结果保留两位小数。AMF-RRNSC、10 layers CNN、MF-VGG16和CRBM均能保证取得给定步数内的最优模型参数，因此可直接将精度曲线极值作为对应模型的最优分类精度。

定义衡量AMF-RRNSC模型在多种小样本环境下性能水平的平均分类精度提升幅度α，计算方法见式(10)，其中N为总对比模型数，αi为第i个对比模型在同一数据集上的分类精度。

(10)

5.1 ESC-50小样本等时长多分类实验

由图8-图10的epoch-accuracy变化曲线可知，经100个epoch后各模型的分类精度均趋近收敛，AMF-RRNSC模型的分类精度为91.14%，10 layers CNN为79.75%，MF-VGG16为84.81%，CRBM为89.87%。

图8 AMF-RRNSC和10 layers CNN在ESC-50数据集对比

图9 AMF-RRNSC和MF-VGG16在ESC-50数据集对比

图10 AMF-RRNSC和CRBM在ESC-50数据集对比

计算可得在ESC-50数据集上，AMF-RRNSC模型的α约为6.33%，进一步分析图8-图10可知，10 layers CNN、MF-VGG16等较浅层网络的精度曲线均在平缓上升后更早收敛，AMF-RRNSC模型的精度曲线则在40 epoch后开始突变性上升，最终在30个epoch内迅速逼近收敛，且收敛精度较浅层网络更高，说明残差结构在分类过程中发挥了作用，与CRBM模型相比，虽然两者的曲线走势相近，但AMF-RRNSC在曲线平滑度和分类精度上具有优势。

5.2 music speech小样本等时长二分类实验

从图11-图13可知，经100个epoch后各模型的性能均不再有大幅变化，可认为精度已收敛，AMF-RRNSC模型的分类精度为96.00%，10 layers CNN为92.00%，MF-VGG16为94.41%，CRBM为92.00%。

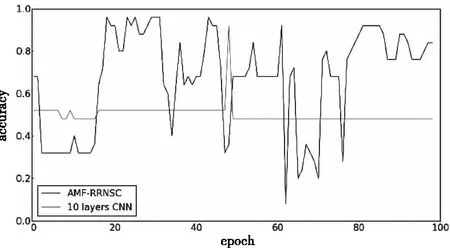
图11 AMF-RRNSC和10 layers CNN在music speech数据集对比

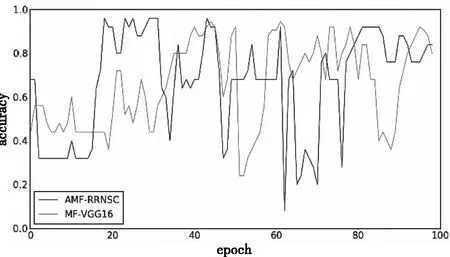
图12 AMF-RRNSC和MF-VGG16在music speech数据集对比

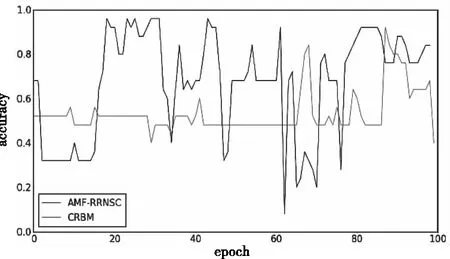
图13 AMF-RRNSC和CRBM在music speech数据集对比

从精度上升情况看，在小样本二分类极端场景下四个模型的曲线平滑度均不是特别理想，各个模型的分类精度差异不大，但AMF-RRNSC模型在精度、曲线平滑度和性能稳定性上仍优于其它三者。由于二分类时总样本数量过少，CRBM模型此时的分类精度反低于MF-VGG16模型，与10 layers CNN模型持平。计算可得AMF-RRNSC模型的α约为3.20%，说明在高区分度频谱图和循环残差的共同作用下，小样本音频分类精度确实能有效提高。

5.3 FSCMC小样本不等时长多分类实验

由图14-图16可知，对有855个类别的FSCMC数据集而言，迭代100个epoch后各模型的精度均已收敛，AMF-RRNSC模型分类精度为94.72%，10 layers CNN模型分类精度为82.28%，MF-VGG16模型分类精度为87.96%，CRBM模型分类精度为92.61%，计算可知α约为7.10%。

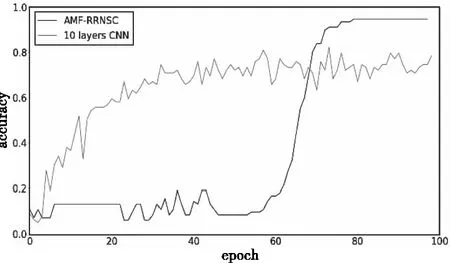
图14 AMF-RRNSC和10 layers CNN在FSCMC数据集对比

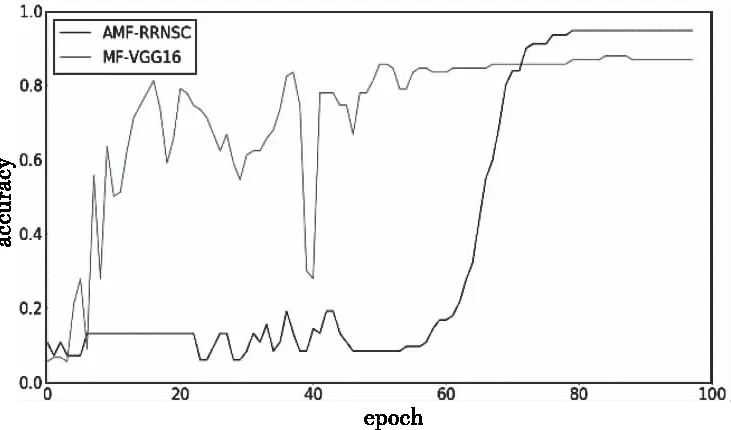
图15 AMF-RRN和MF-VGG16在FSCMC数据集对比

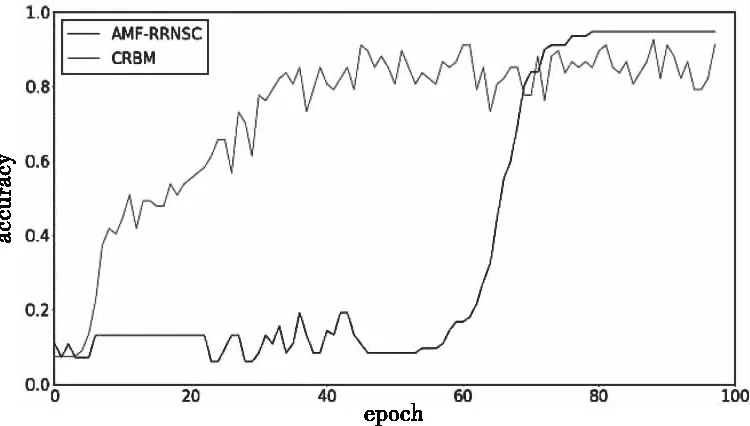
图16 AMF-RRNSC和CRBM在FSCMC数据集对比

深入分析实验结果，与实验4.1比较可知在类别提高一个数量级后各模型的分类精度均有提升。其中AMF-RRNSC模型在epoch为60-80区间时迅速上升，随后分类精度开始收敛，说明在该区间模型找到了较好的残差参数；10 layers CNN的分类精度全程上升较平滑，但最终趋近的分类精度最低，说明朴素CNN模型在小样本下分类精度确有不足；MF-VGG16收敛最快，分类精度好于10 layers CNN，但曲线存在较大突变，稳定性不佳；CRBM模型分类精度仅次于AMF-RRNSC。在FSCMC数据集上AMF-RRNSC模型的α最高，考虑到FSCMC数据集样本总数远多于ESC-50，且各样本时长不等，说明样本间差异越大、类别越多时AMF-RRNSC模型性能相对参照对象越有优势。

5.4 ESC-50&music speech小样本不等时长多分类实验

据图17-图19，经100个epoch后各模型的分类精度均收敛，AMF-RRNSC模型的分类精度为95.24%，10 layers CNN为83.81%，MF-VGG16为88.57%，CRBM为93.33%，计算可知α约为6.67%。与ESC-50数据集相比，ESC-50&music speech中音频信号间的区分度更大，综合参考实验4.1和4.3的结果可知，当类别量下降一个数量级、样本复杂度增加后，各模型的分类精度均有提升，这进一步说明区分度确实是重要的影响分类精度的因素，侧面证明AMF算法的可行性。

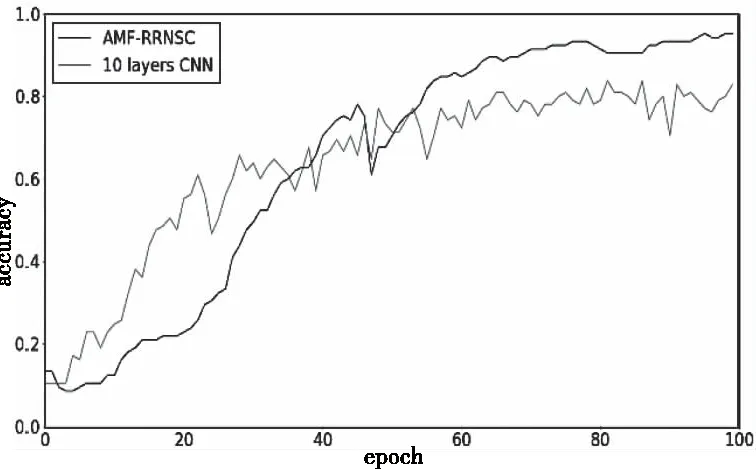
图17 AMF-RRNSC和10 layers CNN在ESC-50&music speech数据集对比

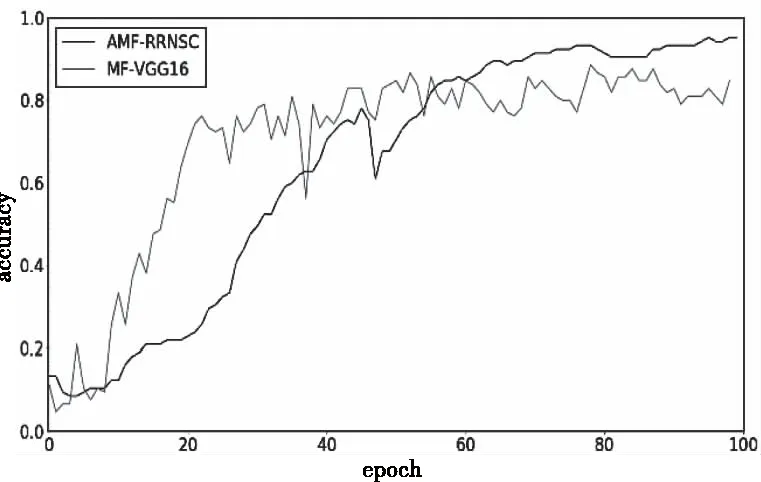
图18 AMF-RRNSC和MF-VGG16在ESC-50&music speech数据集对比

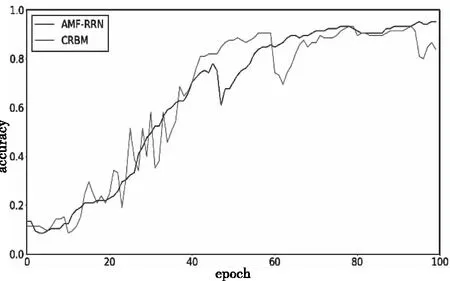
图19 AMF-RRNSC和CRBM在ESC-50&music speech数据集对比

5.5 小结

从表3的实验结果看，在所有数据集上层数最少的10 layers CNN模型分类精度均最低，说明同等条件下深层网络确有更高精度极限。细分到每一个数据集和对照模型，AMF-RRNSC模型的分类精度都更有优势，四组实验共同证明AMF-RRN模型在小样本音频信号分类领域的分类精度和曲线平滑度、模型稳定性均更佳，其中实验4.1和4.3突出证明残差结构在小样本音频分类中的积极作用，实验4.3、4.4从侧面说明AMF算法的有效性。

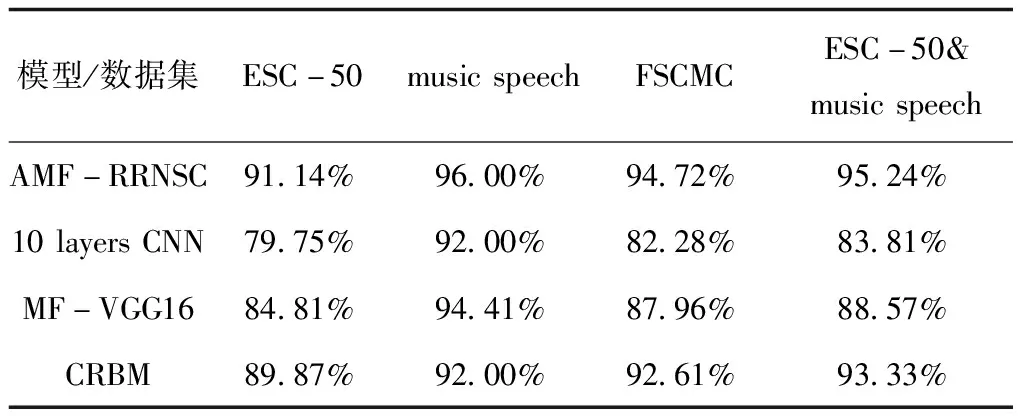
表3 分类精度(越高越好)

6 总结与展望

以梅尔滤波和残差网络为理论基础，提出自适应梅尔滤波算法和循环残差网络分类器，将两者融合构建AMF-RRNSC小样本音频分类模型。使用不同数据集分别模拟等时长小样本二分类、等时长小样本多分类、不等时长小样本多分类等多种场景，并用多组对照实验对AMF-RRNSC模型进行充分验证，结果证明模型的精度更高、曲线更平滑稳定，在等时长小样本多分类、等时长小样本二分类和不等时长小样本多分类场景下均取得了预期结果。

在二分类场景下AMF-RRNSC模型还存在长时间无法有效优化等不足。此外实验结果提示在小样本下模型的分类性能并非随着待分类类别数的增多而单调上升，产生该现象的原因值得深入思考。因此在以后的工作中，将探索精度与类别数间的关系，并尝试通过改进AMF-RRNSC模型的结构，优化参数，在滤波过程中引入选择性注意机制等方法，提升AMF-RRNSC模型在小样本二分类场景下的性能。