基于清晰度信息与灰度差异熵的图像修复算法
2022-03-15庄丽华薛彩霞
刘 俊,庄丽华,薛彩霞
(1.常州大学阿里云大数据学院,江苏 常州 213164;2.常州大学信息科学与工程学院,江苏 常州 213164)
1 引言
在当下信息技术飞速发展的时代,数字图像已被人们广泛接受,用于信息的传播。在数字图像的传播过程中,难免会出现图像的损坏[1-2]。损坏的图像视觉效果较差,不能较好的适应人们对信息传播的需求。对此,人们对图像修复技术进行了研究。利用一定的方法和手段,采用图像中的已有信息,对损坏内容进行修补,以获取视觉效果较好的图像[3]。目前图像修复技术已被广泛应用到了包含广告制作、艺术品复原等多个生活领域[4]。
经过人们对图像修复技术的研究,出现了多种图像修复方法。如Wang等人[5]采用图像的结构信息来计算待修复块的优先权,并通过结构一致方法来获取最优匹配块,利用空间变化方法对置信项进行更新,完成图像修复。由于该算法是通过图像的结构信息计算待修复块的优先权,没有考虑图像的清晰度信息,而且算法采用固定大小的样本块来获取最优匹配块,从而使得修复图像中含有振铃现象。Qian等人[6]在图像结构信息的基础上,优化了优先权计算过程,并采用图像的稀疏特征,对样本块大小进行自适应的调整,利用图像的旋转不变特性,获取最佳相似块,以修复图像。虽然该方法对优先权计算过程进行了优化,但优化过程没有考虑图像的清晰度信息,使得修复图像中含有模糊现象。He等人[7]为了避免置信度的快速衰减,设计了置信度更新函数,将统计变换匹配准则与SSD模型相结合,获取最佳匹配块,用于修复损坏区域。虽然该方法中规避了置信度的快速衰减引起的优先权计算错误,但其忽略了图像的清晰度信息,而且该方法中的样本块为统一尺寸,不能较好的适应图像中的纹理变化,从而使得其修复图像中含有块现象。又如Lai等人[8]采用图像的等照度线信息,寻找优先修复块,利用空间差分度量约束方法,获取最适匹配块,进而得到修复结果。由于利用等照度线信息寻找优先修复块的过程,有考虑图像的清晰度信息,而且空间差分度量约束方法缺少对图像色彩信息的度量,从而使得修复图像中具有伪吉布斯效应。
为了改善图像信息的修复质量,本文利用空间频率,测量了图像的清晰度信息,并将其引入到优先修复块的寻找过程中,使得图像的修复顺序更为准确。通过图像的灰度差异信息,构造灰度差异熵模型,以修整样本块大小。结合SSD模型与灰度差异熵模型,准确的匹配出待修复块的最优匹配块,以完成像素缺失区域的填充。采用本文算法对多种损坏图像进行了修复,通过观察本文算法对损坏图像的修复效果,分析了其有效性。
2 本文图像修复算法
通过观察图1所示的本文图像修复算法的过程可以发现,其通过优先权度量、确定样本块大小和计算最优匹配块来实现。

图1 本文图像修复算法的过程
1)优先权度量。利用空间频率模型,对待修复块的清晰度信息进行度量,并将其引入到待修复块的优先权度量过程,以准确合理的计算图像的修复顺序。
2)计算样本块大小。通过对样本块中像素点之间的灰度差异信息进行测量,构造灰度差异熵模型,从度量样本块纹理特征的角度出发,计算了样本块大小。
3)计算最优匹配块。将灰度差异熵模型与SSD模型相结合,构造搜索函数,用于计算最优匹配块,以修复图像。
2.1 优先权度量
通过对待修复块的优先权进行度量,选取优先修复块,可确定图像的修复顺序。Criminisi算法度量优先权P(p)的方法为[9]
P(p)=C(p)D(p)
(1)
式中,D(p)、C(p)为数据项和置信度项,以p为待修复图像I中损坏内容边缘上的一个待修复点,D(p)与C(p)的计算过程为[10]:
(2)
(3)
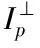
由于随着修复过程不断深入,C(p)会逐渐趋于0,因此从式(1)可见,此时利用D(p)与C(p)做乘法运算求取P(p)的结果就会出错,从而使得优先权的度量变得不合理。对此,本文将采用空间频率模型,对待修复块的清晰度信息进行度量,并将其引入优先权计算,使得优先权的度量过程变得更为准确、合理。
图像的空间频率模型RC,利用大小为M×N图像块W中像素点p(x,y)的灰度特征,计算了该图像块的清晰度信息,其计算过程如下[12]:
(4)
式中,RF、CF分别表示W在行、列上的空间频率,其计算过程如下
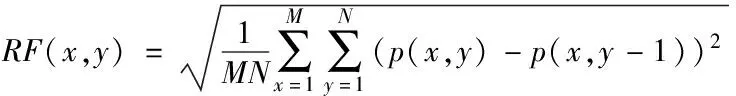
(5)

(6)
(7)
以图2(a)所提的待修复块为样本,利用式(7)来选取其优先修复块,经过多次计算,选取了图像块Lp为优先修复块,结果见图2(b)。

图2 优先修复块的选择
2.2 计算样本块大小
图像修复的过程中,为了适应图像的不同纹理特性,需要对样本块的大小进行计算调整。在图像纹理较为简单时,可适当扩大样本块的尺寸,以使得修复区域具有较好的整体一致性。在图像纹理较为复杂时,可适当缩小样本块的尺寸,以减少块现象的出现[13-14]。本文将利用样本块中像素点间的灰度差异信息,构造灰度差异熵模型,度量样本块的纹理信息,对样本块的大小进行计算,选取适宜的样本块大小用于图像修复。
在图像块Q中,像素点p(x,y)与q(x+Δx,y+Δy)的灰度差异信息Δp为
Δp=|up(x,y)-uq(x+Δx,y+Δy)|
(8)
式中,up(x,y)及uq(x+Δx,y+Δy)分别表示点p与点q的灰度值,(Δx,Δy)为p(x,y)与q(x+Δx,y+Δy)的坐标差值。
将像素点p(x,y)在Q中移动,获取Δp的直方图,并通过直方图求取Δp的概率Δp(i)。接着在Δp(i)的基础上构造灰度差异熵模型ET(p):
(9)
ET(p)反应了Δp对应直方图的分散度,若则直方图的分散度较大,则ET(p)值也随之增大,Q的纹理特征就更为复杂。
利用ET(p)计算样本块大小的过程如下。
1)将样本块大小的起始值设为v×v,并利用式(9)求取此时样本块对应的灰度差异熵值ET(p)j。
2)将样本块大小增大两个像素点为v=v+2。在利用式(9)求取此时样本块对应的灰度差异熵值ET(p)j+1。
3)求取ET(p)j与ET(p)j+1的差异度ΔET(p)
(10)
并将ΔET(p)与阈值φ进行比较,若ΔET(p)≥φ,则表示ET(p)j+1对应的样本块大小纹理过于复杂,不能采用其对应的样本块大小,应该采用增大前ET(p)j对应的样本块大小。若ΔET(p)<φ,则表示ET(p)j+1对应的样本块大小是合理的,此时重复步骤1和步骤2,直到ΔET(p)≥φ为止,方可确定适宜样本块大小。
图3反应了样本块大小的调整过程,通过灰度差异熵函数所确定的样本块大小如图3中的实线框内容所示。

图3 样本块大小的调整
2.3 计算最优匹配块
通过SSD模型可从度量图像的色彩信息出发,计算出与待修复块具有最优相似效果的匹配块。但仅通过SSD模型来计算最优匹配块,可能出现多个最优匹配块的现象,从而使得修复质量下降。而且SSD模型不能较好的度量图像的纹理特征,易造成修复图像的纹理出现断裂现象。对此,本文将SSD模型与灰度差异熵模型相结合,构造搜索函数,用于准确的搜索最优匹配块。
令Lp为待修复块,Mq为θ中的匹配块,则Lp与Mq间SSD模型为[15]:
SSD(Lp,Mq)
(11)
式中,Rx、Gx、Bx为像素点x的R、G、B值。
将SSD模型与灰度差异熵模型相联合,构造的搜索函数SE(Lp,Mq)为
SE(Lp,Mq)=SSD(Lp,Mq)+ΔU(Lp,Mq)
(12)
式中,ΔU(Lp,Mq)为Lp与Mq对应的灰度差异熵的差值,其计算过程如下
ΔU(Lp,Mq)=|ET(p)-ET(q)|
(13)
式中,ET(p)与ET(q)分别为Lp与Mq对应的灰度差异熵值。
利用式(12)搜索最优匹配块的过程如下
Mq=arg minSE(Lp,Mq)
(14)
图4显示了最优匹配块的确定过程以及修复效果。其中图4(a)显示了最优匹配块的确定过程,利用式(14)经过多次计算后,将红色实线框所示匹配块视为了最优匹配块。从图4(b)可见,本文算法修复图像质量较好。

图4 基于最优匹配块的图像修复效果
3 实验结果
实验中采用本文算法、文献[16]和文献[17]算法对损坏图像进行修复,以对各算法的修复效果进行测试。实验平台为IntelCore TM i3-2120 CPU500GB硬盘的LenovoPC机,实验采用的仿真软件为MATLAB R2014a。实验分为修复效果测试与量化测试两个部分进行。实验时本文算法中阈值φ=0.4。
3.1 修复效果测试
不同算法修复划痕损坏图像的效果如图5所示。观察图5(c)可见,其含有振铃和残留现象。从图5(d)可见,其含有边缘断裂和块现象。观察图5(e)可见,其仅含一处轻微的残留现象。图6展示了不同算法修复遮蔽损坏图像的效果。对比各算法的修复效果可见,图6(c)中含有模糊和块现象,图6(d)中含有含有伪吉布斯效应和残留现象,图6(e)中仅有轻微模糊现象。图7为不同算法修复文字损坏图像的效果,对比各算法修复区域可见,图7(d)中含有块现象和残留现象,图7(f)中含有振铃和模糊现象,图7(h)中仅存在一处轻微断裂现象。由此可见,本文算法对多种损坏类型的破损图像都具有较好的修复能力,修复图像的清晰度较高、质量较好。因为本文算法利用空间频率模型度量了图像的清晰度信息,并将其引入到优先权的度量中,提高了修复顺序的合理以及准确性。同时本文算法还通过计算样本块中像素点的灰度差异熵信息,修正样本块大小。从而提高了本文算法的修复能力,及对破损图像的修复质量。
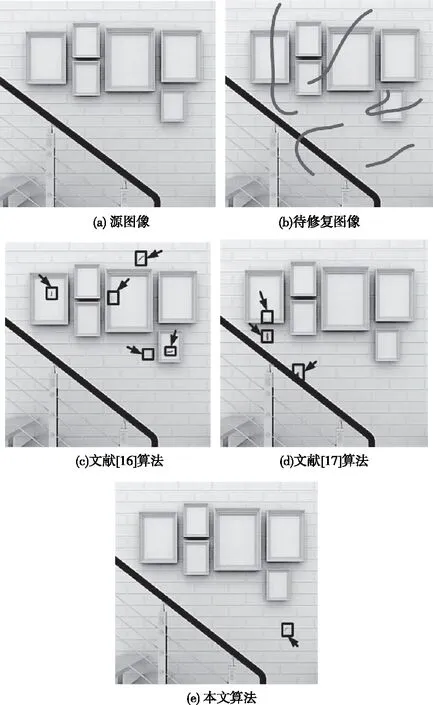
图5 不同算法对划痕损坏图像修复效果
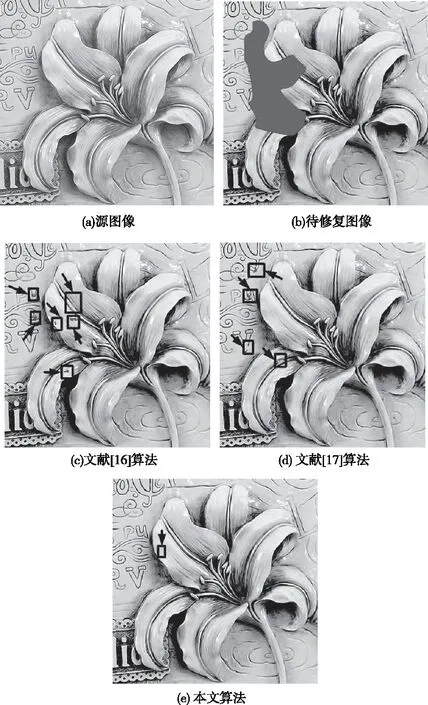
图6 不同算法对遮蔽损坏图像修复效果

图7 不同算法对文字损坏图像修复效果
3.2 量化测试
结构相似度(structural similarity index,SSIM)指标是一种较为常见的修复图像度量指标。修复图像的质量与SSIM指标成正比。本文在图8所示源图像的基础上,获取不同像素缺失比例的待修复图像,并对其修复。利用修复图像的SSIM指标对各算法的修复性能进行量化测试。

图8 源图像
各算法的SSIM指标量化测试值如图9所示。从图9可见,本文算法对大面积破坏程度为52%的像实施后,其对应的SSIM指标为0.892,而此时文献[16]与文献[17]修复图像的SSIM指标为0.785、0.829。通过观察图9可知,本文算法对其它破坏程度的图像修复后,其对应的SSIM指标较其它两个算法的SSIM指标也较高。由此可见,本文算法的修复性能较好,修复图像具有较高的SSIM指标。因为本文算法采用样本块中像素点之间的灰度差异信息,构造了灰度差异熵模型,从度量样本块纹理特征的角度出发,修正了样本块大小。同时本文算法还将灰度差异熵模型与SSD模型相结合,构造搜索函数,用以准确的计算出最优匹配块,对图像进行较好的修复。从而提高了本文算法的修复性能。文献[16]算法中采用了正则化因子,以构造了优先权度量函数,计算图像的修复顺序,同时利用平方误差和函数以及绝对差和函数来选择最佳匹配块,以修复图像。然而,文献[16]算法的优先权度量函数中,没有考虑图像的清晰度信息,而且选择最佳匹配块时,采用的是统一大小的样本块,使得算法不能较好的适应图像的纹理特征,从而导致算法的修复性能不佳。文献[17]算法中将图像块之间的相关特性引入到优先权的度量过程中,并利用样本信息自适应的调整样本块大小,接着通过图像的结构以及欧几里得距离信息,得出最佳匹配块,获取修复图像。但是,文献[17]算法的优先权度量过程,忽略了图像的清晰度信息,而且利用结构以及欧几里得距离信息得出最佳匹配块的过程,不能较好的度量图像的纹理信息,从而降低了图像的修复性能。

图9 各算法的SSIM值测试结果
4 结论
本文利用空间频率模型获取了图像的清晰度信息,并以此为基础,构造了优先权度量函数。以样本块中像素点之间的灰度差异信息为依据,获取了适应图像纹理的样本块大小。将灰度差异熵模型与SSD模型相结合,以准确的搜索出最优匹配块,对图像进行修复。实验中从修复效果和量化测试两个维度对本文算法的修复性能进行了测试,测试结果显示了本文算法具有优良的修复性能。
