从“浅尝辄止”到“寻根究底”
2022-03-15柏德华
柏德华

摘要:数学课堂教学中,教师要善于引导学生探寻数学知识背后的思想方法,使学生“知其然”,更“知其所以然”;要让学生在掌握知识的基础上,体验到数学思维带来的挑战和愉悦,感受到理性思辨的力量。教学《2、5的倍数的特征》一课,不停留于“浅尝辄止”,仅关注知识的表象,而着力于“寻根究底”,追问知识背后的“为什么”,注意思维的科学性和严谨性,让学生的学习深入知识的堂奥。由此得到几点思考:数学课堂要培养学生的理性思维,让研究“寻根究底”;要培养学生的探究能力,让学习“触类旁通”;要培养学生的科学思维,让思考“逻辑自洽”。
关键词:数学知识;数学思维;《2、5的倍数的特征》
一、“浅尝辄止”:《2、5的倍数的特征》教学问题扫描
之前参加教学视导,笔者连续几天听了同一个课题——“2、5的倍数的特征”(苏教版小学数学五年级下册32-33页)的三节课。三节课不约而同地呈现出大致相同的教学流程:以百数表为学习素材,先让学生在表中圈出2、5的倍数,通过观察初步得出它们的特征,然后再举例验证,最后概括出2、5的倍数的特征,并让学生运用该特征判断一些数是不是2、5的倍数。综观教学过程,结合课堂中对学生学习状态的观察,笔者发现了一些问题:
一是教师没有有效激发学生的认知参与,学生处于“浅学习”状态。由于百数表中的数排列规整,2、5的倍数又呈列状分布,特征十分明显,所以学生几乎不用动脑筋就能发现2、5的倍数的特征。学生轻松说出2、5的倍数的特征后,三位执教教师都没有进一步深入下去,追问学生特征背后的原因,所以学生对2、5的倍数的特征“知其然而不知其所以然”。
二是研究方法對于后续内容(3的倍数的特征)的学习不具有统摄性。如何判断一个数是不是2、5的倍数,教材呈现(教师讲授)的研究方法是观察个位上的数。所以,下一节课研究3的倍数的特征时,学生想到的自然也是观察个位,这样就为新知的学习带来了负迁移。换句话说,学生研究2、5的倍数特征的方法不能有效迁移到3的倍数特征的探究上来,这种只观察个位的研究方法对后续学习不具有统摄性。因此,研究2、5的倍数的特征,还应该引导学生从“位值制”的角度分析每一位数字,从而从整体结构上发现规律。叶婉贞.整合联系明晰原理——“2、5、3的倍数的特征”整合拓展的探索[J].小学数学教育,2019(7/8):45。
三是教材的知识逻辑不自洽极易导致教师的教学疏忽。以5的倍数为例,我们知道它的特征是:个位上是5或0。也就是说,“个位上是5或0”是“5的倍数”的充要条件,因此,课堂教学必须要向学生说明以下两点:(1)一个数如果是5的倍数,那么它的个位上一定是5或0(与其等价的逆否命题是:一个数如果个位上不是5或0,那么这个数一定不是5的倍数);(2)一个数如果个位上是5或0,那么这个数一定是5的倍数(与其等价的逆否命题是:一个数如果不是5的倍数,那么这个数个位上就一定不是5或0)。胡晓敏,任敏龙.回到数学原点澄清知识本质——“2、5的倍数特征”教学与评析[J].小学教学参考,2014(20):15。这两点合在一起,才是5的倍数的特征的完整内涵。仔细研读教材,就会发现教材内容有所缺失:只研究了(1)而忽略了(2)。事实上,三位执教教师也都没有注意到这个问题,他们的课堂教学呈现出的是:(1)成立;(2)自然也是正确的,无须另外说明。但教材在研究3的倍数的特征时,显然又注意到了这一点,相关描述为:“如果一个数不是3的倍数,这个数各位上数的和会是3的倍数吗?找几个这样的数算一算。”教师在阅读教材时如果不注意到这个问题,各课时就会顾此失彼,造成教学疏忽。课堂上,教师只有兼顾上述两点,引领学生进行深入的思考、辨析,想通命题背后的原理,才能帮助学生形成对2、5的倍数特征的科学、全面和深刻的认识。
二、“寻根究底”:《2、5的倍数的特征》一课教学改进
基于上述思考与分析,笔者尝试在《2、5的倍数的特征》(以“5的倍数的特征”为例,“2的倍数的特征”的教学思路大致相同,不做赘述)一课教学时,带领学生“寻根究底”。具体教学过程如下:
(一)认识“一个数如果是5的倍数,那么它的个位上一定是5或0”
师上节课,同学们学习了因数和倍数,你能举出一些5的倍数吗?
生5、10、15、20、25、30……
师 (出示百数表)我们把这些数按照一定的顺序放在百数表中。请同学们拿出百数表,在表中圈出5的倍数。
(学生独立在百数表中圈出5的倍数,教师巡视。)
师观察圈出的5的倍数,你有什么发现?
生我发现这些数的个位数字是5或0。
生我发现5的倍数的个位不是5,就是0。
师仅仅依靠百数表中的这20个5的倍数,我们就能得到这个结论了吗?
生(齐)不能!
生我们还要举出大于100的5的倍数,看一下末尾数字是不是5或0。
师请同学们拿出计算器。大于100的第一个5的倍数是——(生:5×21)算算看等于多少?(生:105)个位是几?(生:5)5×22呢?(生:110)个位是几?(生:0)谁再来举例。
生5×37。
生(齐)185,个位是5。
生5×498。
生(齐)2490,个位是0。
……
师同学们举出了这么多5的倍数,有没有发现个位不是5或0的?
生(齐)没有。
师看来,(边说边板书)“一个数如果是5的倍数,那么它的个位上一定是5或0”这句话是——
生(齐)正确的。
(教师面带微笑朝向学生,做迟疑状。多数学生仍坚持原来的看法,少数学生略显犹疑,个别学生陷入思考。)
生不一定。万一举出一个5的倍数,个位不是5或0呢?
师敢于质疑,好样的!是啊,“一个数如果是5的倍数,那么它的个位上一定是5或0”这个结论,我们是通过举例观察得到的。当然,举再多的例子,也不可能穷尽所有5的倍数,所以,要说明这句话是正确的,我们还得从数的原理上想明白其中的道理。同学们,认真想一想:5的倍数,它的个位上为什么不是5就是0,而不可能是其他数字呢?
(教室里出现暂时的静默,过了一会儿,陆续有学生举起了手。)
生第一个5的倍数是5,接着是10、15、20、25、30、35……从5开始,五个五个地数,个位上只能是5、0、5、0、5、0、5……
师你是通过五个五个地数数来理解的,有道理!
生5的倍数都可以用5乘几得到。一五得五,二五一十,三五一十五……五九四十五,五的乘法口诀每句的末尾不是5,就是0。
师你是用乘法口诀理解的。
……
(二)认识“一个数如果个位上是5或0,那么这个数一定是5的倍数”
师同学们已经知道,一个数如果是5的倍数,那么它的个位上一定是5或0。如果一个数只知道个位上是5,其他数位不知道是几,那么它一定是5的倍数吗?(多媒体出示图1,十位和百位由电脑随机生成数字)请同学们用计算器算一算,看看它是不是5的倍数。
师(电脑随机生成三位数145)是5的倍数吗?(生:是)除以5等于多少?(生:29。电脑随机生成三位数695)是5的倍数吗?(生:是)除以5等于多少?(生:139。电脑随机生成三位数875)是5的倍数吗?(生:是)除以5等于多少?(生:175)
……
师会不会出现一个个位是5的三位数,不是5的倍数呢?
生(齐)不会。
师这是为什么呢?
(教室里陷入沉默,学生一时不明白其中的道理。)
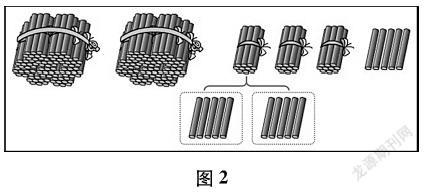
师(多媒体出示图2,边演示边讲解)我们以235为例。十位上的3表示3个十,1个十里有2个5,是5的倍数,那么无论几个十都是5的倍数。1个百里有10个十,20个5,是5的倍数,那么无论几个百也都是5的倍数。所以不管十位上是几,百位上是几,一定都是5的倍数,不用考虑;同理,千位、万位、十万位……都不用考虑了。一个数是不是5的倍数只看个位就行了。235个位上是5,所以235是5的倍数。
生(恍然大悟)我明白了!如果去掉个位上的数的话,就是230,末尾是0,230可以看成23个十,一定是5的倍数,所以只要看个位是不是5的倍数就行了。个位上5的倍数只有5或0,所以个位上是5或0的数,一定是5的倍数。
生不管数有多少位,个位前面的数一定是5的倍数,所以只要看个位。个位是5的倍数,这个数就是5的倍数;个位不是5的倍数,这个数就不是5的倍数。
……
师大家通过讨论,进一步明确了(同步板书)“一个数如果个位上是5或0,那么这个数一定是5的倍数”。
师(小结)同学们,通过刚才的学习,我们得到了两个结论。(教师手指板书,学生齐读)这两条合在一起就是“5的倍数的特征”。
三、几点思考
关于数学课堂教学,有人说:三流教师教知识,二流教师教方法,一流教师教思想。这句话告诉我们,数学教师要善于引导学生探寻数学知识背后的思想方法,“以思想方法的分析带动具体数学知识内容的教学”郑毓信.数学思维与小学数学[M].南京:江苏教育出版社,2008:170。;要能让学生在掌握知识的基础上,体验到数学思维带来的挑战和愉悦,感受到理性思辨的力量。换言之,教师带领学生学习数学知识,不能“浅尝辄止”,仅仅停留于知识的表象,而要“寻根究底”,追问知识背后的“为什么”,并注意思维的科学性和严谨性,让学生的学习深入知识的堂奥。如此,学生获得的数学知识才是鲜活的,可生长的,富有生命力的。
(一)数学课堂要培养学生的理性思维,让研究“寻根究底”
理性思维是一种建立在证据和逻辑推理基础上的思维方式,要求思考问题时“言之有理”“持之有故”。数学学科极其重要的育人价值就是训练学生的理性思维,培养学生的理性精神,使学生不轻信、不盲从,学会“打破砂锅问到底”。
上述教学,不停留于仅让学生通过简单的观察就轻率地得出结论,而是引导学生进一步思考特征背后的原因,从数的本源上想明白其中的道理。比如,当学生通过观察百数表,举例验证得出“一个数如果是5的倍数,那么它的个位上一定是5或0”时,教师并没有让学生轻易接受这个结论,而是反问学生为什么是这样的。实践证明,根据以往的知识积累和学习经验,学生完全可以在自己的认知水平上理解其中的道理。再如,学生认识“一个数如果个位上是5或0,那么这个数一定是5的倍数”时,教师通过小棒图的直观演示,从“位值制”的角度为学生揭示其中的奥秘。在直观图的启发下,学生理解了判断5的倍数的特征不能只看个位数,而是要通盘考虑每一位上的数;由于个位前面的每一位上的数都是5的倍数,所以只要看个位上的数。这样追根溯源地研究5的倍數的特征(2的倍数的特征同样如此),学生对知识的理解就能做到融会贯通。
(二)数学课堂要培养学生的探究能力,让学习“触类旁通”
数学新课程改革特别重视培养学生的探究能力。学生能自主探究的绝不干预;自主探究有困难的,教师要充分发挥主导作用,搭建“脚手架”,帮助学生寻找方法,启发学生理解数学知识的本质。
探究一个数的倍数的特征具有较强的趣味性和探索性。2、5的倍数的特征探究理应对学生后续研究3的倍数的特征具有一定的启发作用。然而,现实情况常常是,学生学习了“2、5的倍数的特征”后,继续学习“3的倍数的特征”时,往往还是观察数的个位,思维陷入窠臼难以自拔。出现这种问题,主要原因在于教师带领学生寻找2、5的倍数的特征时,停留于观察个位上数字的表面特征,没有深究“为什么判断一个数是不是2、5的倍数只要看个位,而不需要看其他数位”,没有通过寻找背后的真相探究出一种研究倍数特征的“通法”。上述“5的倍数的特征”教学,没有停留在“浅学习”的层次,而是引导学生利用“位值制”原理对数进行重组(235=200+30+5),通过分析每一个数位上的数,促进学生真正理解5的倍数特征的本质。经过如此深入的探讨,学生对于2、5的倍数的特征“知其然”,更“知其所以然”。更为重要的是,这种研究方法能有效迁移到3的倍数特征的学习上,从而使得该方法有了“通法”的性质,以后学生再运用同类方法探究4(25)、8(125)、9等数的倍数的特征时,能做到“举一反三”“触类旁通”。苏浙闽,章勤琼.3的倍数特征真的不一样吗——兼谈小学数学中加强联系的通法教学[J].教学月刊·小学版(数学),2020(7/8):98。
(三)数学课堂要培养学生的科学思维,让思考“逻辑自洽”
数学是讲究逻辑的学科,数学课堂是训练学生逻辑思维能力的主阵地。数学教学更应讲求逻辑性,关注思维的科学性和严谨性。因此,根据形式逻辑的要求,数学课堂中的概念、判断、推理等思维形式要符合形式逻辑的基本规律。
如前所述,教学“5的倍数的特征”时,教师需要让学生明白5的倍数的特征包括两方面的内容:(1)一个数如果是5的倍数,那么它的个位上一定是5或0(其逆否命题同样成立);(2)一个数如果个位上是5或0,那么这个数一定是5的倍数(其逆否命题同样成立)。综合这两点,才可以判断一个数是或不是5的倍数。比如,从思维的逻辑性上讲,判断4060是5的倍数,根据是(2),因为4060的个位数字是0;判断273不是5的倍数,根据是(1),因为273的个位数字不是5或0。数学教师要能理清上述数学知识之间的逻辑关系,课堂教学才能做到条理清晰、层层推进、丝丝入扣。培养学生思维的科学性和严谨性,让思考“逻辑自洽”是教学最基本的要求。
3355501908287
