同构变形在函数问题中的应用

田 鹏

(重庆市长寿中学)

在函数问题中,有一部分问题是利用函数的单调性构造出来的,如果能够将这类问题中隐藏的函数模型呈现出来,不仅会加快解题者解决问题的速度,更有助于看清问题的本质.一般而言,若F(x)≥0能够变形成f(g(x))≥f(h(x))的形式,则可利用f(x)的单调性得到g(x)≥h(x)(或g(x)≤h(x)),这种变形的方法称为同构变形.

1 两个引理

引理1设函数f1(x)＝xex,f2(x)＝f3(x)＝,f4(x)＝xlnx,f5(x)＝,f6(x)＝.则有以下结论:f1(lnx)＝f4(x),f2(lnx)＝f6(x),f3(lnx)＝f5(x),f4(ex)＝f1(x),f6(ex)＝f2(x),f5(ex)＝f3(x).

证明因 为f1(lnx)＝elnxlnx＝xlnx＝f4(x),故f1(lnx)＝f4(x)成立,同理,可证其余各式.

注该引理指出这六个函数的内在联系,这是含指数函数与对数函数同构变形的原理.

引理2(1)对任意的x∈R,ex≥x＋1恒成立,当且仅当x＝0时等号成立;

(2)对任意的x∈(0,＋∞),lnx≤x－1恒成立,当且仅当x＝1时等号成立.

证明(1)设函数f(x)＝ex－x－1,则f′(x)＝ex－1,易知f′(x)在R 上单调递增,且f′(0)＝0.当x∈(－∞,0)时,f′(x)＜0;当x∈(0,＋∞)时,f′(x)＞0,故f(x)≥f(0)＝0,即f(x)≥0在R 上恒成立,即对任意的x∈R,ex≥x＋1恒成立,得证.仿照(1)的证明方法,易证得(2)成立.

2 双变量问题

2.1 双变量方程

例1已知实数x1,x2满足x1ex1＝e3,x2(lnx2－2)＝e5,则x1x2＝_______.

分析x2(lnx2－2)＝e5可转化为elnx2－2(lnx2－2)＝e3,进而构造函数解决问题.

解x2(lnx2－2)＝e5可转化为elnx2－2(lnx2－2)＝e3,设函数f(x)＝xex,则f′(x)＝(x＋1)ex.当x∈(－∞,－1)时,f′(x)＜0,当x∈(－1,＋∞)时,f′(x)＞0,所以f(x)在(－∞,－1)上单调递减,在(－1,＋∞)上单调递增.又f(x1)＝f(lnx2－2)＝e3＞0,则x1＝lnx2－2,故

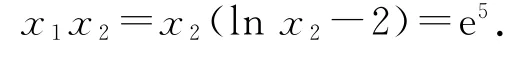
由条件x1ex1＝e3,x2(lnx2－2)＝e5,对比两式的结构特征,将x2(lnx2－2)＝e5同构变形,从而通过构造函数解决问题.

例2已知函数f(x)＝xex,g(x)＝xlnx,若f(x1)＝g(x2)＝t(t＞0),则的最大值为_________.

分析由引理1知g(x)＝f(lnx),同构变形构造函数,利用函数单调性求解.

解因为g(x)＝f(lnx),由f(x1)＝g(x2)＝t,可得f(x1)＝g(x2)＝f(lnx2)＞0.又易知f(x)在(0,＋∞)上单调递增,故有x1＝lnx2,由f(x1)＝g(x2)＝t,可 得x1ex1＝x2lnx2＝t,故x1x2＝x2lnx2＝t,则设h(t)＝则h′(t)＝,故当t∈(0,e)时,h′(t)＞0,当t∈(e,＋∞)时,h′(t)＜0,所以h(t)在(0,e)上单调递增,在(e,＋∞)上单调递减,故h(t)≤h(e)＝,即的最大值为

通过g(x)＝f(lnx)可将方程f(x1)＝g(x2)变为同构方程,从而导出关系式x1＝lnx2,又由x1ex1＝x2lnx2＝t可推导出x1x2＝t,进而构造函数求解问题.

2.2 双变量不等式

例3已知f(x)＝－ax＋(a－1)lnx,证明:当1＜a＜5时,对任意x1,x2∈(0,＋∞),且x1≠x2,有＞－1.

分析由x1,x2的任意性,可假设x1＜x2,将＞－1等价变形为f(x1)－f(x2)＜x2－x1,进而构造函数解决问题.

(1)令h(x)＝f(x)－,求h(x)的单调区间;

(2)设a＞0,且当x1,x2∈(0,1],x1≠x2时,都有|f(x1)－f(x2)|＞|g(x1)－g(x2)|成立,求实数a的取值范围.

分析第(2)问根据函数f(x)和g(x)的单调性,可将|f(x1)－f(x2)|＞|g(x1)－g(x2)|的绝对值去掉,进而同构变形,然后构造函数,再利用函数的单调性解题.

解(1)函数h(x)的单调递增区间为＋∞),单调递减区间为(0)(求解过程略).

(2)易知函数f(x)在(0,1]上单调递增,又g′(x)＝－,因为a＞0,所以g′(x)＜0,故g(x)在x∈(0,1]上单调递减.不妨设0＜x1＜x2≤1,则f(x1)＜f(x2),g(x1)＞g(x2).因此|f(x1)－f(x2)|＞|g(x1)－g(x2)|可变形为f(x2)－f(x1)＞g(x1)－g(x2),即f(x2)＋g(x2)＞f(x1)＋g(x1).令F(x)＝f(x)＋g(x)＝a2lnx－,则有F(x2)＞F(x1),F(x)在(0,1]上单调递增,故F′(x)＝≥0对任意的x∈(0,1]恒成立,即对任意的x∈(0,1]恒成立.设G(x)＝则G′(x)＝＜0,故G(x)在(0,1]上单调递减,故G(x)≥G(1)＝,所以,解得a≤或,又a＞0,所以实数a的取值范围为

将|f(x1)－f(x2)|＞|g(x1)－g(x2)|同构变形为f(x2)＋g(x2)＞f(x1)＋g(x1),再构造函数F(x)＝f(x)＋g(x)＝a2lnx－从而问题转化为函数F(x)在(0,1]上单调递增,最后转化为恒成立问题处理.事实上,针对这一类含双变量的问题,只要仔细观察式子的结构特征,有效转化式子,然后构造函数,就能利用函数的单调性解决.

3 单变量问题

3.1 恒成立问题

例5已知a＜0,不等式xa＋1·ex＋alnx≥0对任意的实数x＞1 恒成立,则实数a的最小值为_________.

分析xa＋1·ex＋alnx≥0等价于xa＋1·ex≥－alnx,进一步变形为x·ex≥x－alnx－a,由引理1可知不等式两边可化为具有相同的结构形式.

解因为xa＋1·ex＋alnx≥0等价于xa＋1·ex≥－alnx,即x·ex≥x－alnx－a.设f(x)＝xex(x＞1),由引理1知x－alnx－a＝f(lnx－a),则不等式变形为f(x)≥f(lnx－a).易知f(x)在(1,＋∞)上单调递增,又a＜0,故lnx－a＝－alnx＞0,故x≥lnx－a,即－a≤.设g(x)＝(x＞1),则g′(x)＝,当x∈(1,e)时,g′(x)＜0,当x∈(e,＋∞)时,g′(x)＞0,所以g(x)在(1,e)上单调递减,在(e,＋∞)上单调递增,则g(x)≥g(e)＝e,故－a≤e,即a≥－e,所以实数a的最小值为－e.

事实上,常见的含指数函数和对数函数的不等式问题主要有以下几种类型:1)若x1ex1≥x2lnx2,则可构造函数f(x)＝xex,f(x)＝xlnx或f(x)＝x＋lnx;2)若,则可构造函数或f(x)＝x－lnx;3)若ex1±x1≥x2±lnx2,则可构造函数f(x)＝x±lnx或f(x)＝ex±x.以上这些类型皆可结合指数函数与对数函数的关系以及引理1进行证明,留给读者自证.

例6已知函数f(x)＝ex－aln(ax－a)＋a(a＞0),若关于x的不等式f(x)＞0恒成立,则实数a的取值范围为( ).

A.(0,e] B.(0,e2)

C.[1,e2] D.(1,e2)

分析不等式f(x)＞0等价于ex－aln(axa)＋a＞0,考虑同构变形,则不等式变形为ex＞aln(ax－a)－a,即ex＞alna＋aln(x－1)－a,即ex－lna－lna＞ln(x－1)－1,即ex－lna＋x－lna＞ln(x－1)＋x－1,进而构造函数解决问题.

解由f(x)＞0,可得ex－aln(ax－a)＋a＞0,即ex＞alna＋aln(x－1)－a,即ex－lna－lna＞ln(x－1)－1,两边同时加上自变量x,可得ex－lna＋x－lna＞ln(x－1)＋x－1.设函数h(x)＝ex＋x,则不等式变为h(x－lna)＞h(ln(x－1)),易知h(x)在R上单调递增,有x－lna＞ln(x－1),即lna＜x－ln(x－1).设g(x)＝x－ln(x－1),则g′(x)＝,由题知x＞1,当x∈(1,2)时,g′(x)＜0,当x∈(2,＋∞)时,g′(x)＞0,所以g(x)在(1,2)上单调递减,在(2,＋∞)上单调递增,故g(x)≥g(2)＝2,则lna＜2,解得0＜a＜e2,选B.

本题先对ex－aln(ax－a)＋a＞0同构变形,再构造函数h(x)＝ex＋x解题.

3.2 放缩问题

例7已知函数f(x)＝lnx＋x－xex＋1,则函数f(x)的最大值为________.

分析若直接求导分析函数f(x)的单调性,不仅运算量大,而且会遇到导数零点不可解的情况.因此,可利用同构变形解题.

解因为f(x)＝lnx＋x－xex＋1＝lnx＋xelnx＋x＋1,由引理2知elnx＋x＋1≥lnx＋x＋2,当且仅当lnx＋x＋1＝0 时等号成立(事实上,存在x0∈(0,＋∞),使得lnx0＋x0＋1＝0 成立,读者可自行证明).所以f(x)≤lnx＋x－(lnx＋x＋2)＝－2,故函数f(x)的最大值为－2.

xex＋1可变形为elnx＋x＋1,则函数f(x)变为f(x)＝lnx＋x－elnx＋x＋1,结合引理2,利用ex≥x＋1可得elnx＋x＋1≥lnx＋x＋2.当然,本题也可直接求导分析导函数的正负,从而得到函数f(x)的单调性,进而求得最值.不过,其中涉及隐零点的代换且运算量较大,感兴趣的读者可查阅关于隐零点问题的相关文献.事实上,由引理2可导出更多的不等式,例如,对任意的x∈R,ex≥ex恒成立;对任意的x∈(－1,＋∞),ln(x＋1)≤x恒成立.

例8已知函数f(x)＝xex－ax2,g(x)＝lnx＋x－x2＋1－,且a＞0,若关于x的不等式f(x)－ag(x)≥0 恒成立,则实数a的取值范围为_________.

分析由不等式f(x)－ag(x)≥0,可得xex＋e≥a(lnx＋x＋1),进而同构变形,参变分离求解.

解不等式f(x)－ag(x)≥0可转化为xex＋e≥a(lnx＋x＋1),即elnx＋x＋e≥a(lnx＋x＋1).当lnx＋x＋1≤0 时,不等式恒成立,此时a∈R;当lnx＋x＋1＞0时,不等式变为a≤,而当且仅当lnx＋x＝1(事实上,存在x0∈(0,＋∞),使得lnx0＋x0＝1成立,读者可自证)时等号成立,此时a≤e.又a＞0,综上,实数a的取值范围为(0,e].

不等式xex＋e≥a(lnx＋x＋1)可根据lnx＋x＋1的正负进行讨论,由ex≥ex对任意x∈R 恒成立,当且仅当x＝1时等号成立,可得elnx＋x≥e(lnx＋x)对任意x∈R 恒成立,当且仅当lnx＋x＝1时等号成立.由此可见,在处理含指数函数与对数函数的方程(或不等式)时,首先将式子同构变形,再结合不等式放缩,可以使解答简洁明了.

具有相同结构形式的方程(或不等式)问题都可以利用同构变形来解决,值得注意的是,这种问题并不是只能利用同构变形来解决,可能会有多种解决方法.不过,对于这种问题,利用同构变形可以化难为易,化繁为简.利用同构变形的关键是认清形式,合理变形,将方程(或不等式)变为同构形式,进而构造函数解决问题.因此,对常见的基本同构形式以及同构变形的策略进行总结,积累解题经验,树立同构意识是很有必要的.

(完)