基于稳定图分组加权的最优模态参数自动识别算法研究

焦恒昌

（中国电子科技集团公司第二十二研究所，山东青岛，266100）

结构模态参数用于表征结构的固有动态特性，试验模态分析主要通过控制系统激励，对结构系统的输入时域信号和输出时域信号进行同步测量，通过时域或者频域的数学算法处理得到系统频响函数(频域)或者传递函数(时域)，利用曲线拟合等方法识别出系统的频率、阻尼和振型[1]。多参考点最小二乘复频域法（PRLSCF）是国际近年发展并流行的基于系统传递函数的模态分析方法，该方法对系统模态的频率、阻尼和振型都有很好的识别精度[2]。而在实际的工程应用中，输入输出信号的测量、传输中会有环境噪声的影响，得到的数据质量是有区别的，数据的有效性也参差不齐。一方面多参考点最小二乘复频域法处理过程中对不同质量数据做了同等对待，影响模态识别精度；另一方面，目前人工手段借用稳定图进行的模态参数识别，对操作者个人素质要求较高，影响方法便捷应用。

本文针对PRLSCF算法中对不同质量数据缺少有针对的区别合理对待利用，以及人工拾取稳定图中物理模态自动化程度低，研究了基于稳定图分组加权的最优模态参数自动识别算法。

1 理论分析

1.1 加权综合频响函数

PRLSCF算法模态参数识别技术利用系统输入输出得到多个频响函数,构造频响函数矩阵。在频域中，系统输出和输入的关系可用右矩阵分式模型（RΜFD）来描述[2]，右矩阵分式模型的表达式为：

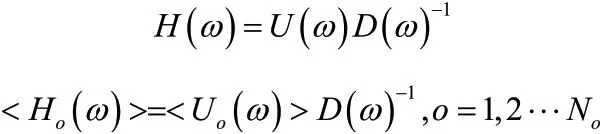
且Uo(ω)和D(ω)可以表示成如下形式：

式中：N—多项式阶次

其中:

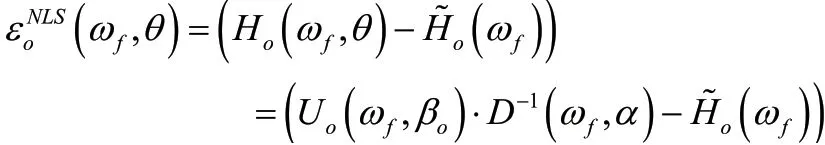
对于参数矩阵θ做非线性最小二乘（NLS）目标函数为：

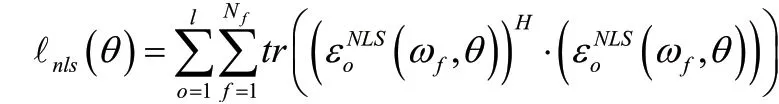
式中：•H：矩阵的复共扼转置；

tr(•)：矩阵的迹，即矩阵的主对角元素之和。

利用数学方法求上式极小值，便得到θ矩阵的估计值。

因此通过试验测量输入输出数据数据质量高低，直接影响结构系统测量频响函数逼近真实系统频响函数程度，进而对最终模态参数识别精度产生直接影响。

定义加权综合频响函数：

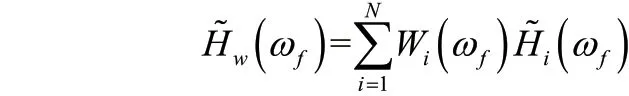
其中：

加权综合频响函数不再是多次试验结果频响函数的简单平均，而是充分考虑每次试验的频响函数质量，即每次输入与输出的相干函数作为加权函数，当频响函数质量较高则在加权频响函数中具有较高的权值，频响函数数据质量劣质时则在加权函数中权值较低。这样即达到提高优质数据在计算过程中的权重，提高模态参数识别精度。

1.2 基于稳定图分组加权的最优模态参数自动提取

在模态分析中，稳定图是分离结构物理极点和数学极点（虚假极点）的有力工具[3]。稳定图的建立方式为：坐标轴横坐标为频率，单位Hz，坐标轴纵坐标为的阶次值，图上标注特定文字符号。由于利用稳定图模态识别需要对模型阶次假设，且假设阶次要高于系统固有阶次，通过计算得到物理模态及计算虚假模态。但是一般实际情况是随模型假设阶次递增，物理模态作为真实模态，始终保持稳定在一条轴上；而通过计算出现虚假模态则随机离散出现，散布于稳定图上，不会出现类似于真实模态稳定轴。根据结构系统这个性质，便比较直观在稳定图上区别开物理模态和虚假模态。根据工程经验，系统假设的阶次取值越大，在稳态图上反映的极点信息越全面，防止出现漏掉的稳定极点，也便于出现稳定轴；但是阶次估值提高也带入了许多虚假的极点信息，这样会给极点分离带来困难。这就要需要权衡估计阶次高低的优劣，选取合适估计阶次。

稳定图上不同估计阶次情况下极点分布，在同一模态轴上，相邻阶次模态参数相比较，若相邻阶次模态参数差值不高于容差设定值，则该极点为稳定极点，得到的模态参数为稳定模态参数。假定特征频率容差为f∆ ，阻尼比容差为 ξ∆，则稳定点的条件为：

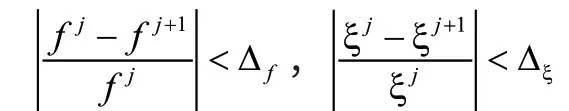
其中j表示系统模型阶数，f、ξ表示不同估值阶次下的模态频率、阻尼比。

通过专家人工对模态极点筛选的步骤，可将模态识别过程划分为：首先选择理想的极点列，然后在列中选择比较好的极点，进而对系统进行模态参数识别。因而进行自动化模态参数识别的基础是按照专家筛选过程对每一步的标准进行量化。主要分为以下几个步骤：

①基于加权的最优极点列提取

根据不同模态参数识别方法，假定不同模型固有阶次，得到的所有计算极点（即虚假极点）将散布于整个稳定图上。系统固有模态并不会随着模型阶次的提高而大的改变，而计算的虚假模态则会随着模型阶次提高而变化较大。

在整个需要分析频带内分成若干频带组，一般是每组带宽为整个分析频带的0.5%~1.0%，若是模态更为密集，则可根据具体情况相应提高分组组数，得到标准组列。但存在边界与固有频率重合情况，利用标准分组再偏移半个标准组带宽得到新的偏移组列，统称为极点列，如图1所示。

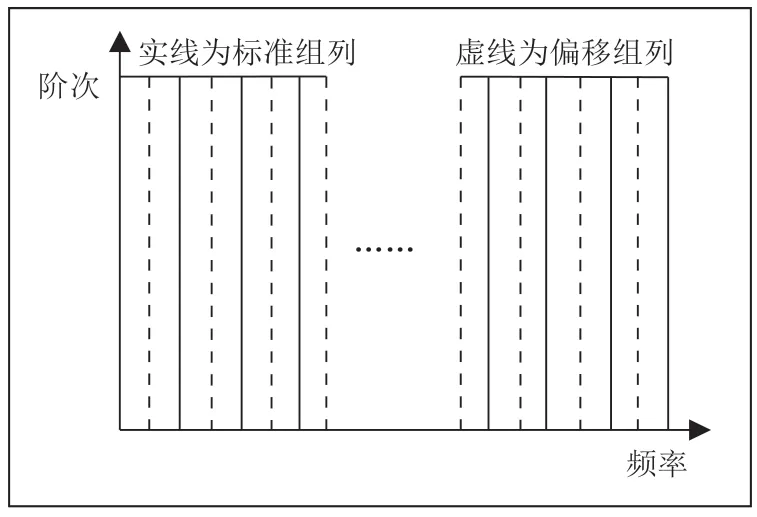
图1 稳定图频带组分组示意图

将每个标准组列及偏移组列中的极点通过加权计算该组总分值，其中“s”类权分ws，“d”类权分wd，“v”类权分wv，“f”类权分wf，得到每一组的极点列加权分值：

根据最终加权分值的大小，得到前N个基于加权的最优极点列 {Si}。

②加权最优极点簇选择

得到最优极点列后，需要选择最优极点列 }{iS中的最优极点作为模态极点。但是极点列中有很多极点，为了减少虚拟极点混入，首先将每极点列分成若干极点簇，选择最优极点簇，整个流程如图2所示。

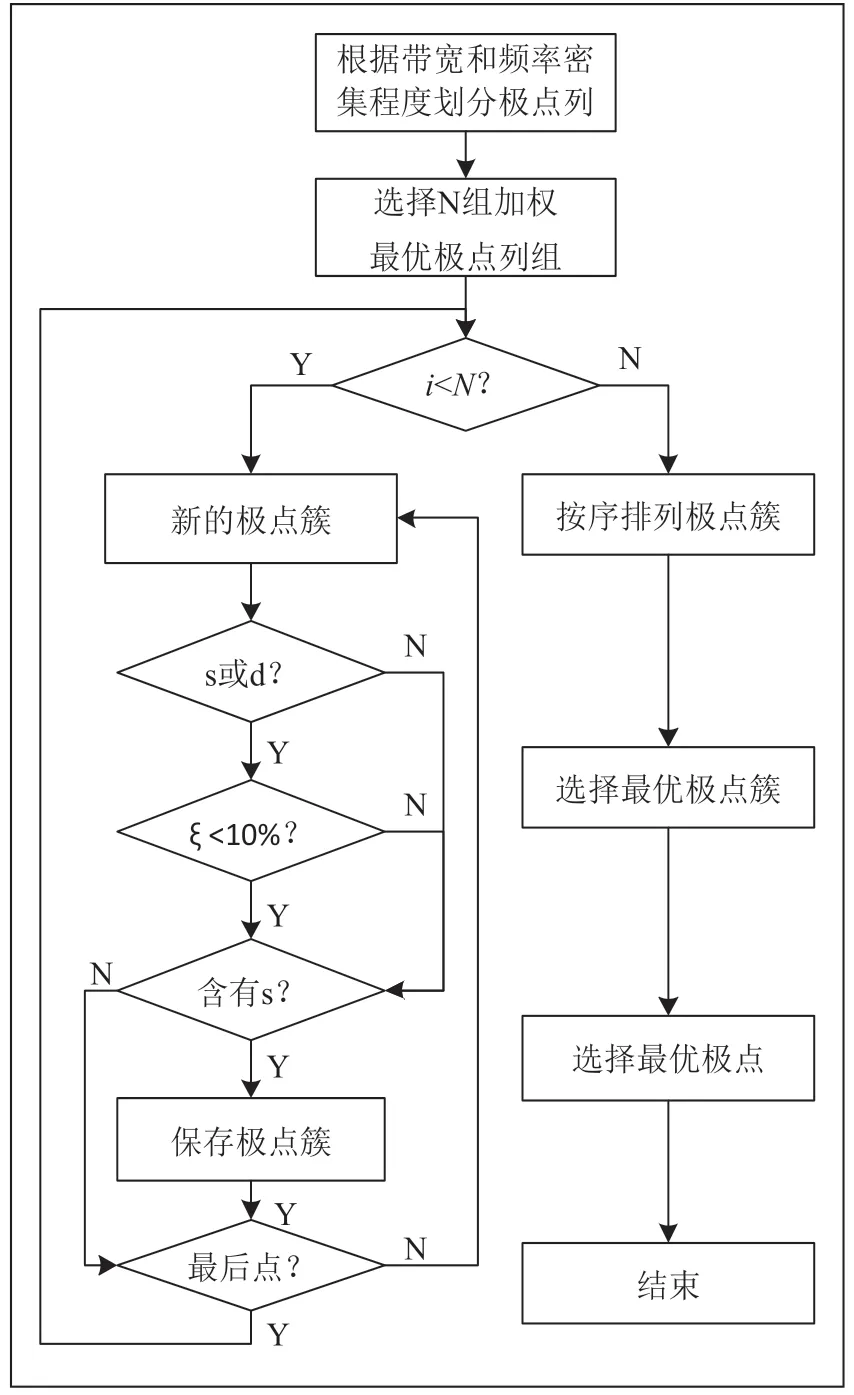
图2 加权最优极点极点簇选择流程图

③最优稳定极点选择

在最优极点簇选择平均阻尼比相差最小的极点作为最优稳定点。

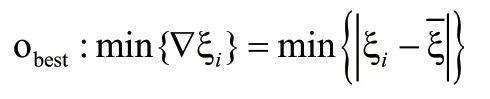
因此，整个基于稳定图分组加权的最优结构模态参数自动提取过程为：首先根据多次测量的数数输出采集数据计算实测频响函数矩阵，利用相干函数作为加权函数构造加权的综合频响函数矩阵，然后根据实际分析频带设定出最高假定阶次，利用多参考最小二乘复频域法构造稳定图，最后利用基于稳定图分组加权自动拾取最优稳定极点，对系统模态参数进行计算。整个过程流程图如图3所示。

图3 基于稳定图分组加权的最优模态参数自动提取流程图

2 实验论证与分析

为了验证方法的有效性，以一个三自由度线性时不变系统作为仿真结构[4]，如图4所示。

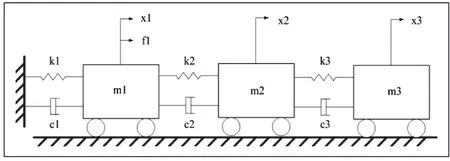
图4 三自由度线性时不变振动系统

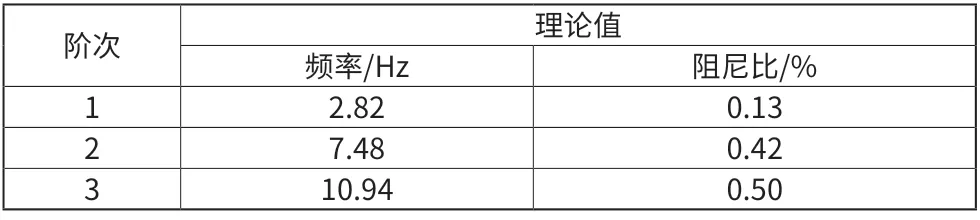
表1 系统的频率和阻尼比理论值

对系统中m1激励，激励类型为脉冲激励，力大小f1=1kN，同步对3个质量块时域位移响应信号采集，设置采样频率40Hz，采样时长150s。得到各点位移响应如图5所示。由图5看出各测点位移响应已经得到很好的衰减，不需要加窗函数处理。

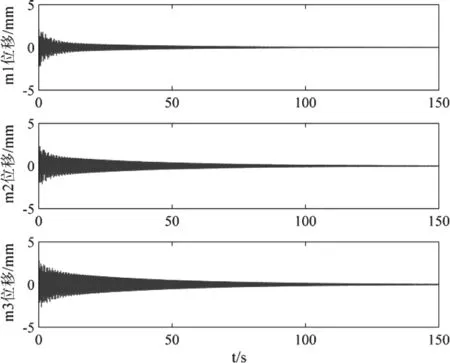
图5 三自由度系统位移响应时域图

对输入输出响应分别加1%，5%，10%的随机噪声作为模拟三次采样数据，并根据输入输出并做频率响应函数，以m1为例如图6所示。

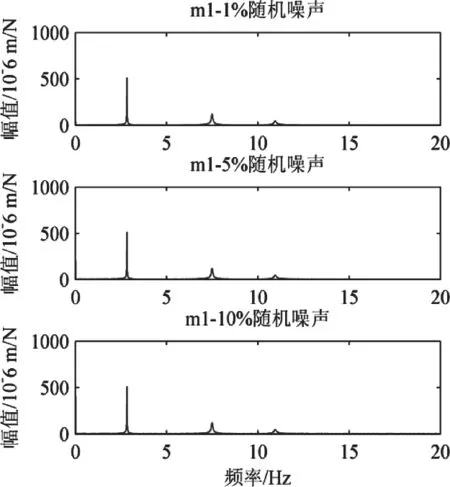
图6 m1不同噪声下频响函数曲线

对不同加噪处理后的输入输出信号处理，分别计算系统频响函数矩阵和相干函数矩阵，进而可计算平均频响函数和本文方法的加权综合频响函数。利用以上数据对系统分别采用PRLSCF和改进PRLSCF进行模态分析，假设模型最高阶数为64，分别得到系统稳定图如图7、图8所示。

结合图7和表1看出，稳定图上在系统固有频率处出现了由稳定点（s）所构成的清晰稳定轴，但在非固有频率出也出现了稳定轴，即计算出的虚假稳定轴。因此这些虚假稳定轴在模态拾取就会被误拾取，计算出多余错误的模态识别结果。在图7，图8稳定图中虚假稳定极点明显减少，在系统固有频率处的稳定轴更加明显清晰，使得拾取稳定轴变得更加容易，模态参数识别可操作性更强，减少结构系统模态参数识别中误判率。

图7 PRLSCF方法构造的稳定图

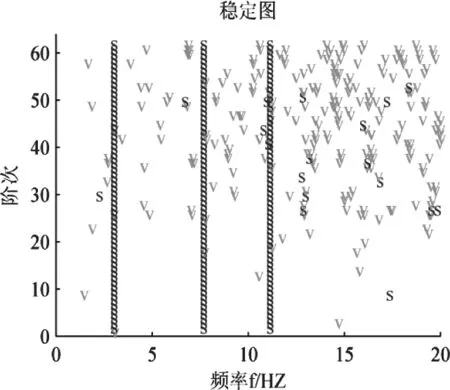
图8 改进PRLSCF方法构造的稳定图

最后基于稳定图分组加权的最优结构模态参数自动提取识别结果如表2所示。可以看出，多参考最小二乘复频域法和本文的方法都可以得到系统的三阶固有模态参数，但是在阻尼比和固有频率识别的精度上，本文方法比原有的多参考最小二乘复频域法误差更小，更接近于理论值。

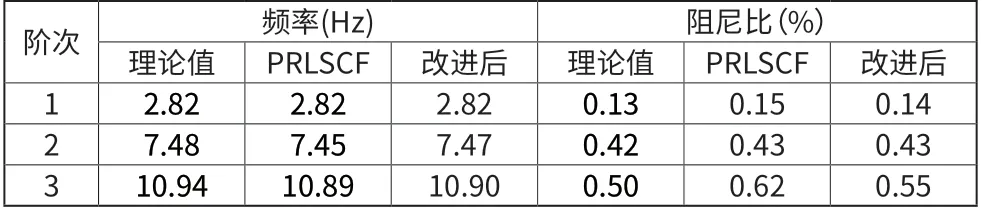
表2 两种方法识别结果对比

3 结束语

对现有PRLSCF模态参数识别算法进行优化并提出基于稳定图分组加权的最优结构模态自动识别算法。对PRLSCF模态识别算法进行优化，提出加权的多参考最小二乘复频域法模态参数识别，以输入输出相干函数为加权函数得到综合频响函数，通过增加高质量采集数据的权重，更加有效利用高质量采集数据，提高系统模态参数识别精度；提出了基于稳定图分组加权的最优结构模态参数自动识别，根据稳定图中计算模态的频率、阻尼比等分组加权，自动拾取最优物理极点并进行模态参数计算，提高了模态分析自动化程度。最后通过仿真的三阶物理模型进行系统模态参数识别，本文方法比原PRLSCF法构造出的稳定图更加清晰，可实现自动识别模态参数，验证了本文方法的可行性与正确性。