一种改进的捷联惯导三子样划桨误差补偿算法∗

耿腾飞 刘 明 陈世强

（云南民族大学 昆明 650031）

1 引言

在捷联惯性导航系统中，由于载体位置的不断变化，加速度计和陀螺常常受到不同程度的线运动与角运动的干扰，导致在对加速度计的比力信息进行积分时存在划桨误差，对陀螺的输出信息进行积分存在圆锥误差，因此在更新过程中必须对其进行补偿。目前已经有大量学者对于圆锥误差的补偿算法进行了一系列的研究［1～4］，有效地提高了姿态解算的精度；也有不少学者针对划桨误差的补偿算法做了大量的研究与改进［5～9］，来提高速度解算的精度。文献［10］利用算法的对偶性原理，根据圆锥误差的一般形式得到了划桨误差补偿的一般形式；文献［11］利用已求得的姿态矩阵，推导出一种新的划桨误差补偿积分算法，此算法计算量小，精度高；文献［12］针对角增量划桨误差补偿算法直接应用于角速率捷联惯导中误差增大的现象，推导出基于角速率的划桨误差补偿系数方程。本文通过划桨误差与圆锥误差的对偶关系，提出一种采用前一周期速度增量和角增量的改进三子样划桨误差补偿算法，经过对比分析改进后的算法精度有所提高。

2 划桨效应

选取“东北天”地理坐标系为SINS的导航坐标系，速度基本方程为

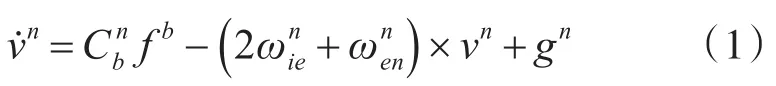
对式（1）在tm-1到tm时间段进行积分，可得：

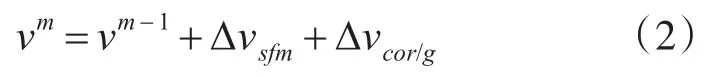
其中：

由于

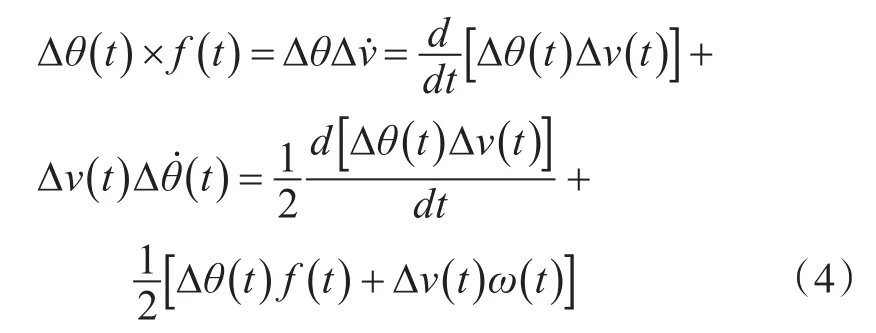
将式（4）代入式（3）可得到：

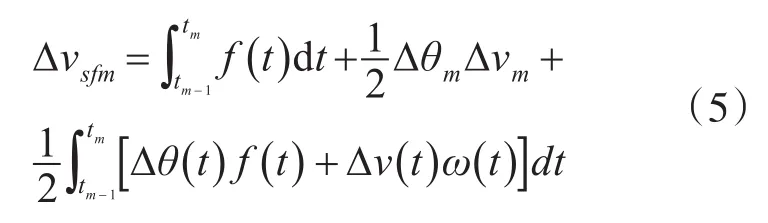
式中最后一项为划桨误差补偿。

3 传统划桨误差补偿算法

文献［5］给出了传统划桨误差补偿算法的一般形式，并详细推导了划桨误差补偿系数的过程，与圆锥误差补偿算法具有对偶性，可得三子样算法为

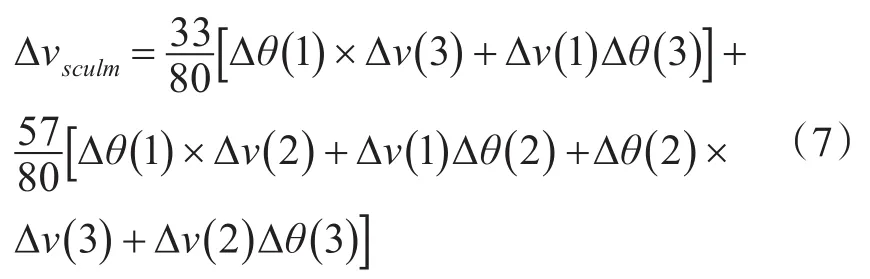
可验证与圆锥误差补偿算法系数相同，算法具有对偶性，上述是用多项式拟合得到，但是实际中载体运动十分复杂，以算法漂移误差最小为标准，可得优化三字样算法：

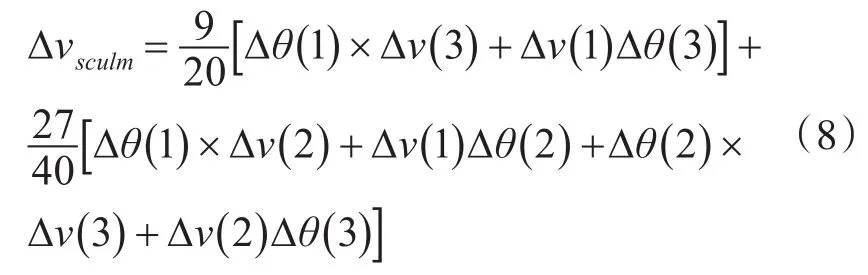
4 改进划桨误差补偿算法

参考利用前一周期陀螺角增量信息改进圆锥误差补偿的算法，改进划桨算法的一般形式为m-1为前一时刻补偿周期，G为补偿系数。

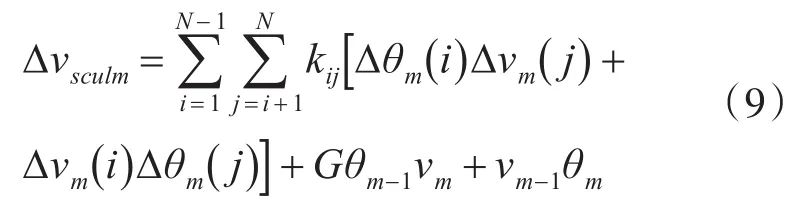
文中对改进的三子样算法进行详细的推导计算。

设更新周期为T，假设典型的划桨运动中角速度和比力为

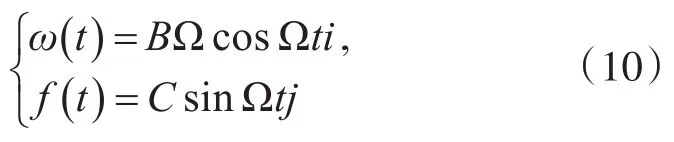
i,j是两正交轴的单位矢量，B,C为角振动和线振动幅值，Ω为振动角频率。

由式（9）可得补偿公式为

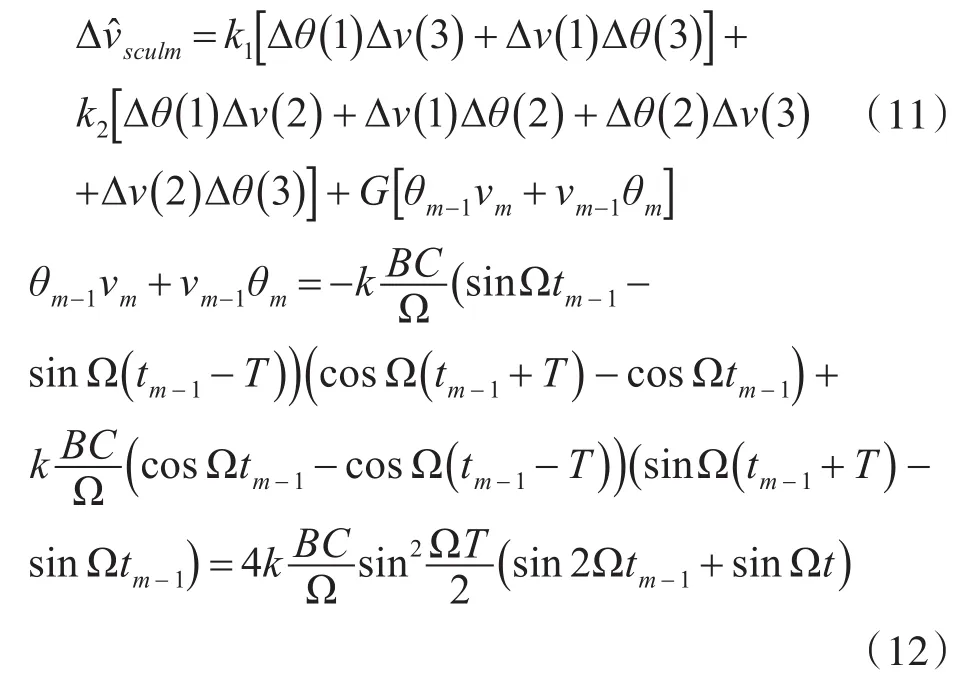
当仅考虑直流分量时：

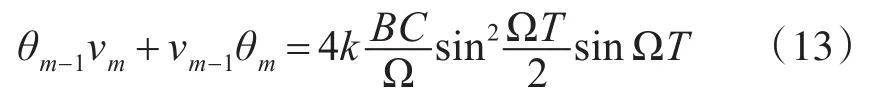
仅考虑直流分量时又有以下恒等式：

将式（13）和式（14）代如式（11）得：

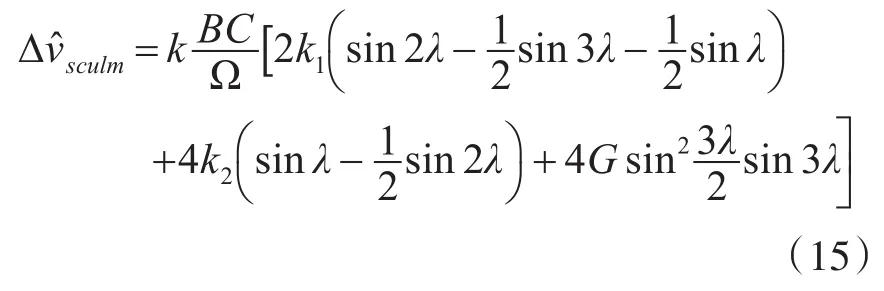
由文献［10］可知，传统划桨效应的补偿值为

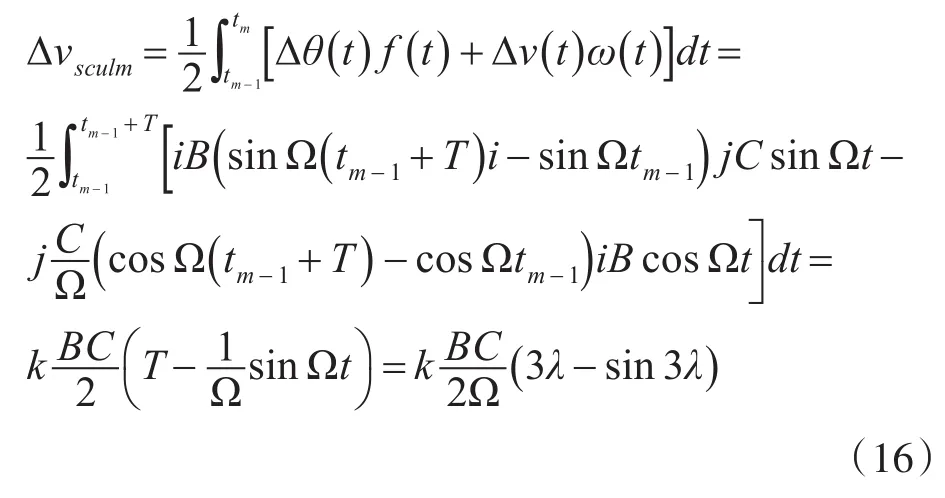
由此可得改进三子样算法误差为

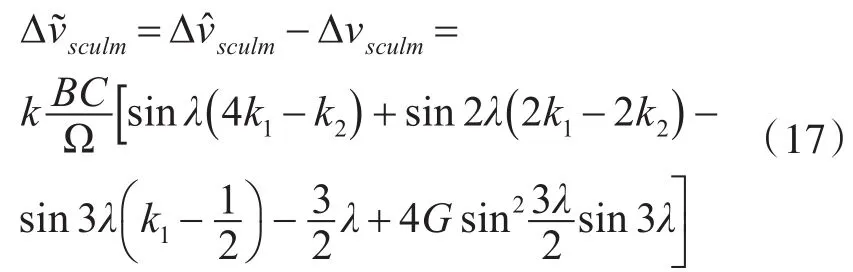
可以得到方程组如下：

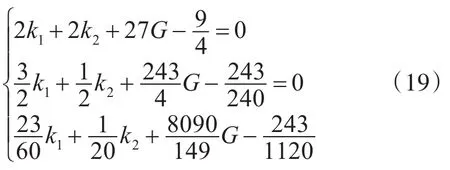
解得：

可得改进算法误差为

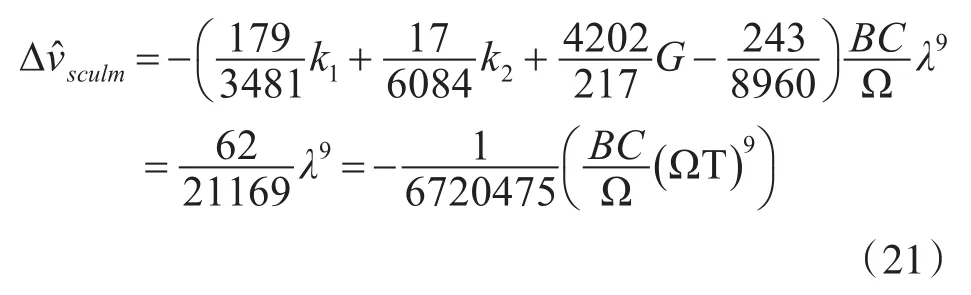
通过式（19）令G=0，同样可得传统三子样算法方程组如下：

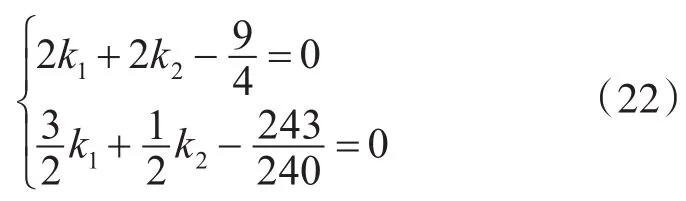
可解得：

所得系数与传统三子样划桨误差算法系数完全一致，从侧面验证了推导过程的正确性。

传统三子样算法误差为

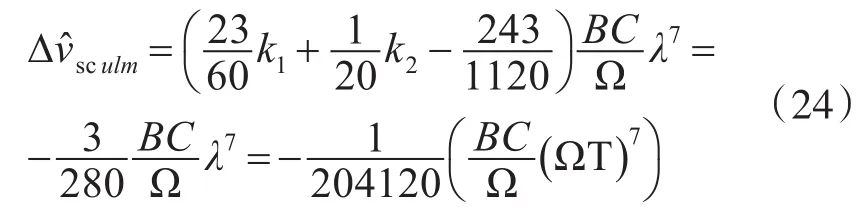
根据式（21）和式（24）的结果，可以看出误差比传统算法有明显的减小。

令B=0.5,C=0.2,T=0.1，两种算法的误差如表1所示。其误差曲线图如图1所示。

表1 不同振动频率Ω下的算法误差

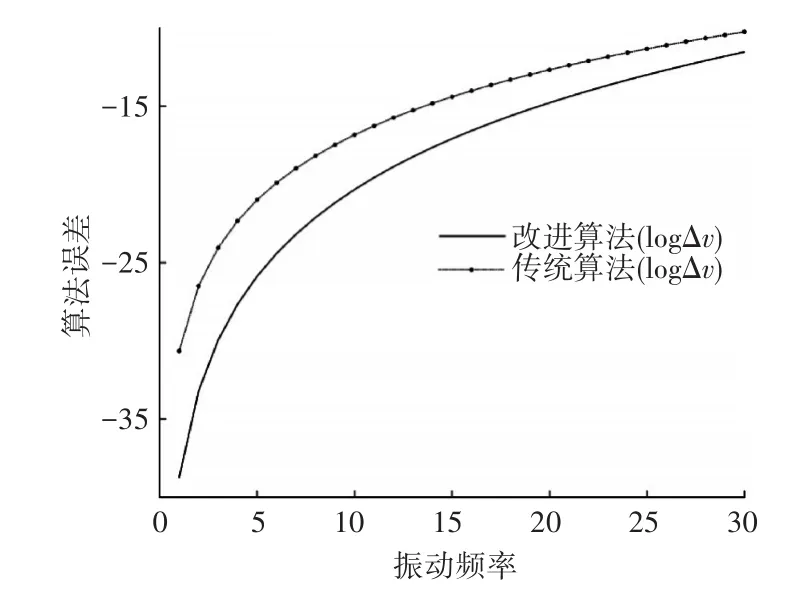
图1 算法误差与振动频率Ω的关系

经分析可知不管是传统算法还是改进算法都与振动频率Ω有关系，且随着振动频率Ω的增大而增大，在相同频率下，可以看出改进算法有明显的优势。

5 结语

文中依据圆锥误差补偿算法与划桨误差补偿算法的对偶性，提出一种采用前一周期速度增量和角增量的改进三子样划桨误差补偿算法，利用算法漂移误差最小原则，详细推导了误差补偿系数，并依据此算法求出传统划桨三子样补偿系数，通过比较可知新算法精度有所提高，具有一定的应用价值。