基于2D-MUSIC的MIMO雷达目标估计∗
2022-03-14朱泽锋
朱泽锋 陈 庚
(中国人民解放军91913部队 大连 116041)
1 引言
由于 MIMO(Multiple Input Multiple Output)雷达对隐身目标和远距离弱目标的探测优势[1],其在军事领域的应用也日益广泛,近几十年来,随着电子技术创新成果的不断涌现与数字信号处理技术的迅猛发展,雷达理论得到了进一步的完善,雷达的种类也不断丰富,按发射与接收天线阵分布方式的不同,可分为单基地雷达、双基地雷达、多基地雷达等。目前MIMO技术已经在无线通信领域中获得巨大成功,由于通信和雷达原理的相似性,为MI⁃MO技术引入到雷达研究领域创造了条件[2]。MI⁃MO雷达根据阵元布置方式可定义为集中式MIMO雷达[3~4]和分布式MIMO雷达[5]。集中式MIMO雷达的阵元布置间距较小,与传统相控阵雷达不同的是其发射波形相互正交,正因为正交波形特性,接收天线可对接收的混合信号进行匹配滤波处理,从而分离出相对于不同发射天线的信号,即集中式MIMO雷达拥有波形分集特性,相比相控阵雷达,其具有更好的空间目标探测能力和参数估计性能[6]。集中式MIMO雷达按体制可分为单基地和双基地两种,双基地雷达设置有距离较远的发射阵和接收阵,收发阵内的阵元布置较密集,本文将针对双基地MIMO雷达开展研究。
目前有多种算法应用于MIMO雷达的研究[7~10],而MUSIC算法是传统的阵列信号处理算法[11],该算法利用信号子空间和噪声子空间的正交性,构造空间谱函数,基于搜索谱函数的峰值来完成MIMO雷达的波离方向角(Angle of Departure,AOD)和波达方向角(Angle of Arrival,AOA)的估计。MUSIC算法对于天线阵列的结构没有特殊要求,对于均匀线阵、L型阵列以及圆阵列都有很高的估计性能。本文在双基地MIMO雷达的目标角度估计研究中引入2D-MUSIC算法,实验表明其能较准确地估计出目标角度值。
2 集中式双基地MIMO雷达数学模型
2.1 雷达模型
雷达模型采用均匀线阵(Uniform Linear Ar⁃ray,ULA),如图1所示,其M个阵元等距离均匀地排列成一条直线,假设各个阵元之间的距离为d,波长为λ,信号源与均匀线阵法线的夹角为θ,则均匀线阵的方向向量为
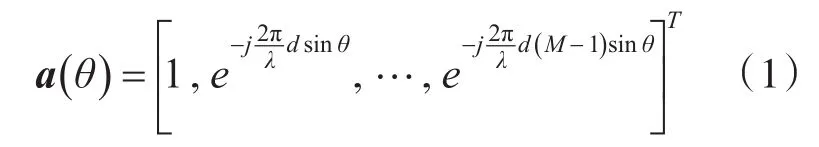
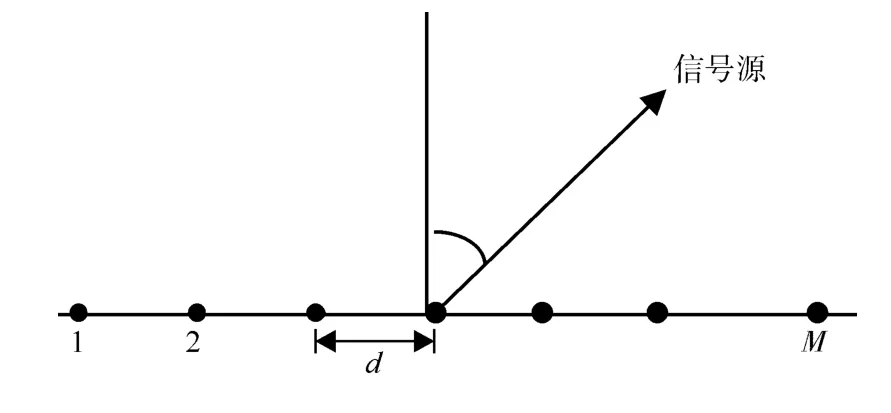
图1 均匀线阵
假设待检测目标的数目为K,其波达方向角分别为θi(i=1 , 2 ,… ,K),则可得到由方向向量组成的形式为范德蒙矩阵的方向矩阵
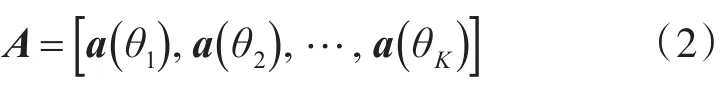
双基地MIMO雷达的模型如图2所示。假设目标为远场点目标,收发信号为窄带信号。
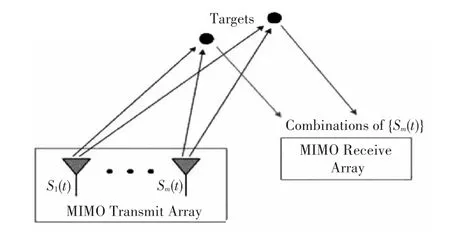
图2 双基地MIMO雷达模型
雷达模型假设发射天线M个,接收天线N个,天线发射正交窄带脉冲信号,脉冲采样点数为L,其信号即为总发射信号可由表示。
2.2 接收混合信号模型
假设共有K个目标,第k个目标的波离角是φk波达角是θk,信号波长是分别表示第m个发射阵元和第n个接收阵元与各自阵列第一阵元的间距,则对于接收阵和发射阵的目标导向矢量分别为
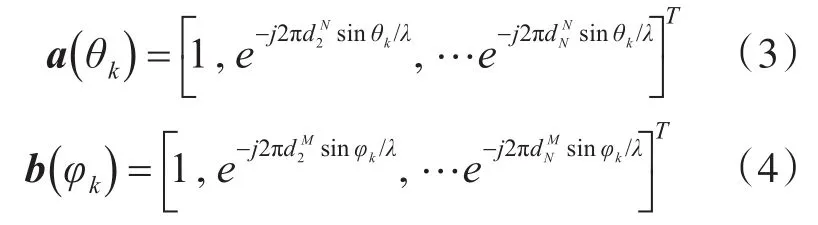
那么接收阵接收端处理的混合信号为
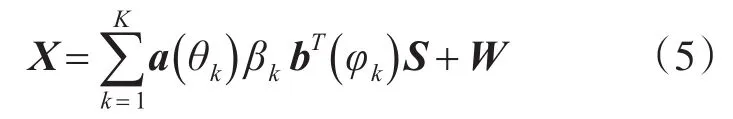
式中,βk表示第k个目标的截面积衰落系数,W∊ℂN×L是高斯白噪声。其矩阵形式为[12]
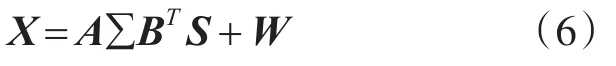
式中,X∊ℂN×L表示N个接收阵元接收的L点采样值的混合信号,
2.3 滤波信号模型
针对接收信号(6),Q个脉冲的情况可写为
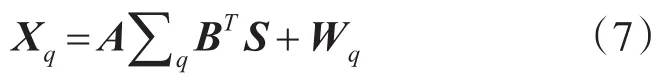
本文使用Swerling II型信号模型,即截面积衰落系数随脉冲独立变化。而相互正交的发射信号的协方差矩阵(1L)SSH=IM。则对式(7)右乘(1L)SH,即匹配滤波后得

其向量化形式为

式 中q=1 , 2 , … ,Q。 考 虑 Q 个 脉 冲 情 况 并 写成矩阵形式

3 目标角度估计的2D-MUSIC算法
对单基地MIMO雷达来说,有M=N,θk=φk。假设待检测目标数目为K,抽样点数为L。传统的MUSIC谱函数可以写成
式中,X是接收信号,EX是N×(L-K)阶矩阵,为噪声子空间,可以通过X的奇异值分解获得。
对于双基地MIMO雷达来说,针对接收信号数据模型(10),计算其协方差矩阵:

进一步将其分解为
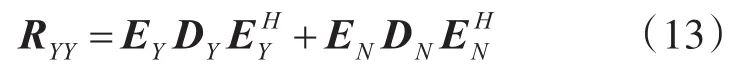
式中,DY是一个K×K阶对角矩阵,它是由K个最大的特征值所构成的,DN是由MN-K个较小的特征值所构成的对角矩阵。EY是与K个最大的特征值所对应的特征向量,定义为信号子空间,EN是剩余的较小的特征值所对应的特征向量,定义为噪声子空间。模型中信号子空间与噪声子空间相互正交,可以构造出2D-MUSIC算法的空间谱函数,其表达式为
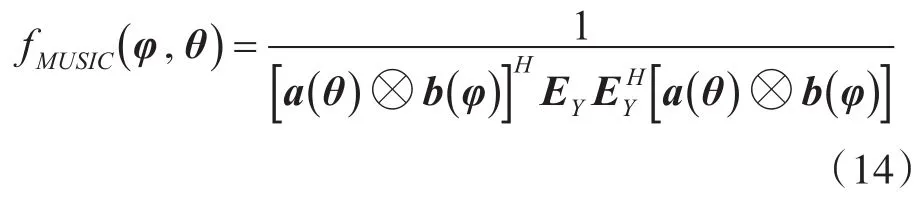
2D-MUSIC算法计算每对AOD和AOA的空间谱函数,然后二维搜索普函数,其前K个峰值所对应的角度值,即为AOA与AOD的估计值。
4 仿真实验
本文使用2D-MUSIC算法做仿真实验,估计双基地MIMO雷达模型中多个目标的角度。模型设置载波频率是fc=1GHz,λ=c/fc,d=λ/2,脉冲间隔5×10-6s。目标数K=5,用φk和θk表示第k个目标的波离角和波达角。
4.1 2D-MUSIC空间谱函数
2D-MUSIC对空间谱函数进行二维搜索,将其前K个最大值相应的角度作为波离角和波达角的估计值。本文使用Matlab工具,仿真式(14)的2D-MUSIC空间谱函数图像,二维搜索间隔为1°,如图2所示。
本文设置目标波离角和波达角分别为(40°,25°)、(35°,30°)、(30°,45°)、(-45°,60°)及(60°,-35°),其中三个目标的距离较近。其中脉冲数为Q=50,采样点数为L=512,信噪比为10dB。在图3中可知,收发阵元数M和N为3时,即可较准确地估计出两个较远的目标。当收发阵元数为7时,可较准确地估计出五个目标。综上可得出,随雷达模型收发阵元数目的增加,目标估计精度大幅提高。
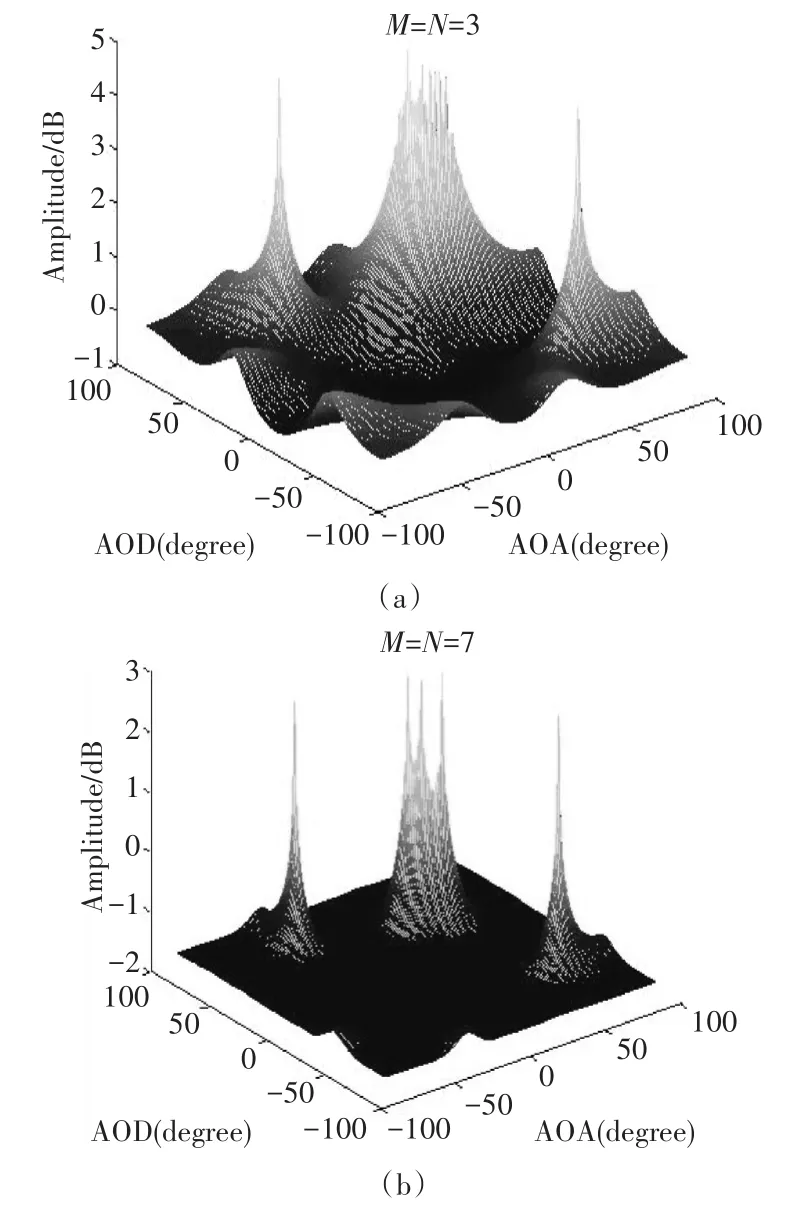
图3 2D-MUSIC空间谱函数
4.2 估计目标角度
如图4所示,5个目标的波离角和波达角为(40°,25°)、(35°,30°)、(30°,45°)、(-45°,60°)及(60°,-35°),脉冲采样点数L=512 ,收发阵元M=N=7,信噪比SNR=10dB。左图为真实目标角度,右图为2D-MUSIC算法估计出的目标角度。仿真实验表明2D-MUSIC算法可以较准确地估计出多个目标的波离角和波达角。
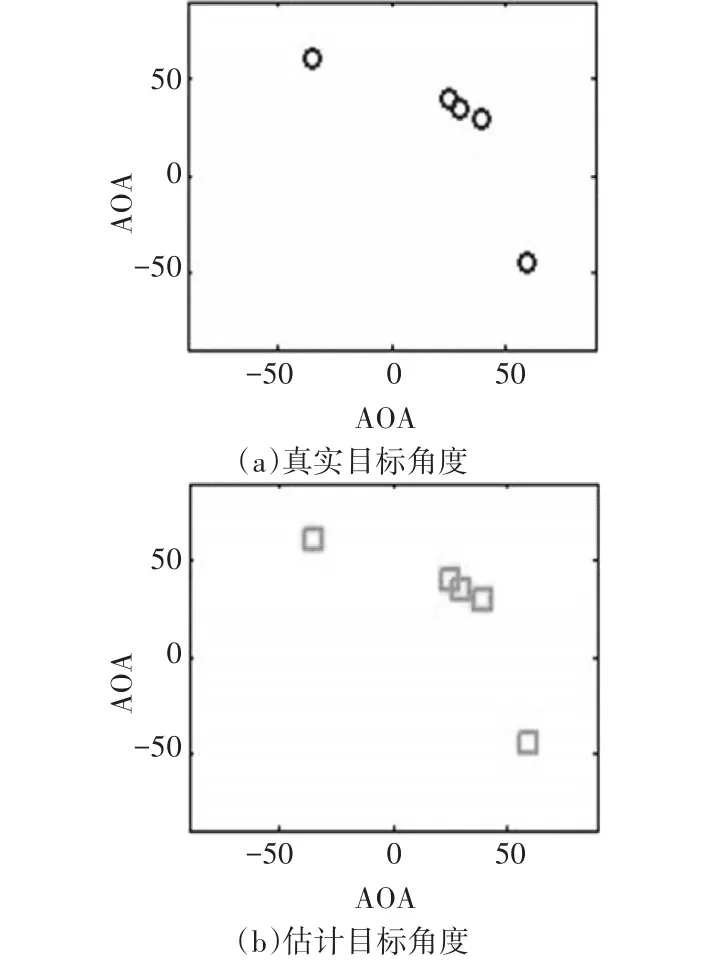
图4 目标角度估计图像
5 结语
围绕现代战争对隐身弱目标的探测需求,本文在集中式双基地MIMO雷达模型的多目标角度估计研究中引入2D-MUSIC算法。本文建立双基地MIMO雷达数据模型,获取接收混合信号模型,推算出通过匹配滤波的信号模型。然后对双基地MI⁃MO雷达模型,运用2D-MUJSIC算法估计多个目标的波离角和波达角,在收发阵元较少时,其对距离较近的多目标角度估计精度受到限制,通过适当增加收发阵元数目,可以有效提高目标估计精度。通过最后的仿真实验可知,基于2D-MUSIC的双基地MIMO雷达的多目标角度估计具有较好的有效性和准确性。
