航空反潜鱼雷搜捕概率分析∗

郭 聚 韩建立 李新成 吕照富 周云飞 李军东

（1.海军航空大学 烟台 264001）（2.中国人民解放军65529部队 辽阳 111000）（3.中国人民解放军61267部队 北京 101123）

1 引言

随着潜艇威胁的增加，高效的反潜措施变得异常重要。潜艇具有较低的噪声辐射、其依赖隐蔽性高的特性潜伏在海中难以被发现，而相比之下，它可以很容易地识别攻击水面舰艇或来袭鱼雷［1］。因此，为了提高攻潜效率，攻潜鱼雷必须相对潜艇较近的距离发射，使得潜艇没有足够时间完成机动或对抗。这使得空投鱼雷成为最有效的攻击潜艇的武器之一［2］。在航空反潜作战中，携带空投鱼雷的航空反潜机接收到吊放声呐探测定位到的潜艇位置信息后，迅速携带鱼雷飞往指定坐标进行投雷，由于多种误差共同作用，使得鱼雷落水点与理想落点存在误差［3］，落点误差、投雷点与潜艇的方位、距离都会影响空投鱼雷的搜索概率。本文将结合落点误差讨论空投鱼雷投雷距离与方位对搜索概率的影响。

2 鱼雷模型建立

2.1 坐标系转换

鱼雷坐标系中od为鱼雷的重心或形心。令轴沿鱼雷运动航向；轴与鱼雷运动航向垂直并定义向上为正；轴与轴和轴构成的平面垂直并服从右手系。

将鱼雷坐标系转换到地理坐标系中，可以通过鱼雷质心在地理坐标系中的三个坐标点和两坐标系之间的夹角可以用鱼雷三个姿态角来描述，如图1所示。

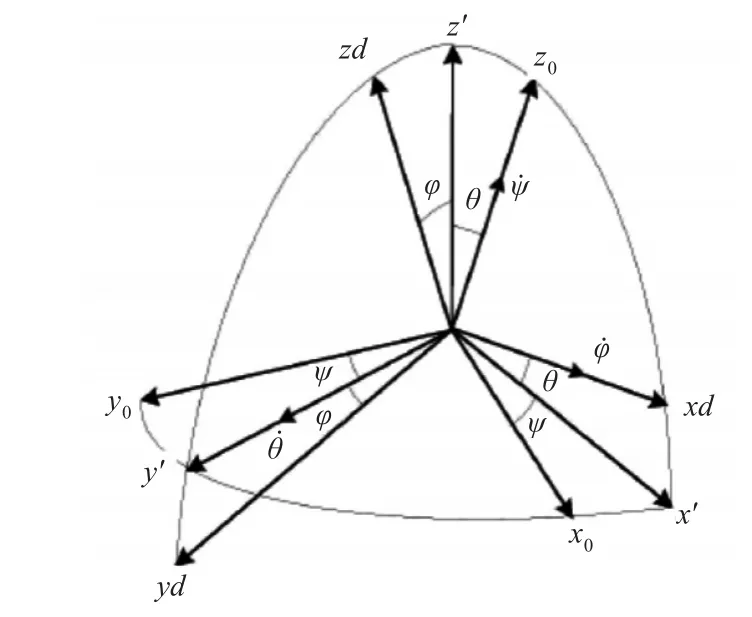
图1 鱼雷姿态角

图1中θ为鱼雷的俯仰角、ψ为鱼雷的偏航角、φ为鱼雷的横滚角。(xd,yd,zd)为鱼雷在鱼雷坐标系中的坐标，(x0,y0,z0)为鱼雷在地理坐标系中的坐标，故有：

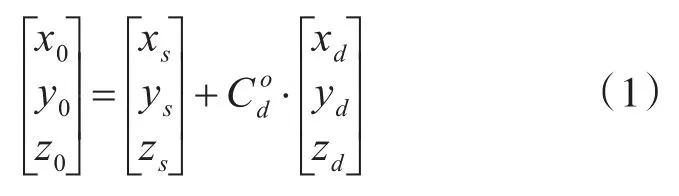
式中：

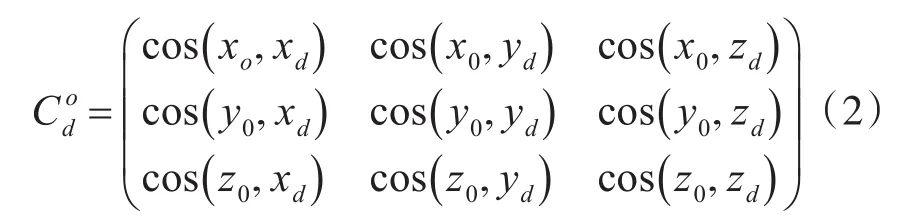
称式（2）中各元素为方向余弦，表示两坐标系之间相应各轴的夹角的余弦，坐标系的转换可以理解为鱼雷姿态角的旋转，即：

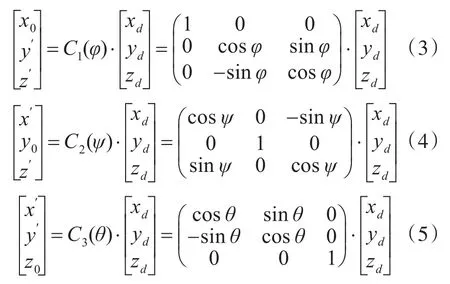
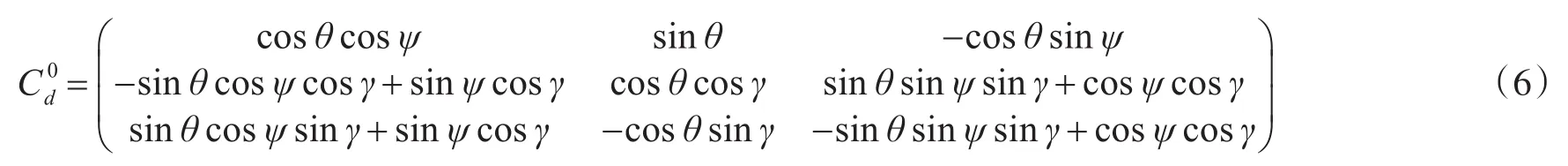
2.2 环型弹道模型

由于鱼雷运动在垂直面的运动状态比较单一，为简化考虑在模拟中只考虑水平面的运动，如果需要可对垂直面的运动进行分解［4］。假设鱼雷环形角速度为ωT（定义向左运动为正向，）tc时刻在坐标(Xc,Yc,Zc)点进行环形搜索，定义鱼雷初始位置为原点，初始时刻鱼雷航向为y1轴。所建环形搜索模型如图2所示。

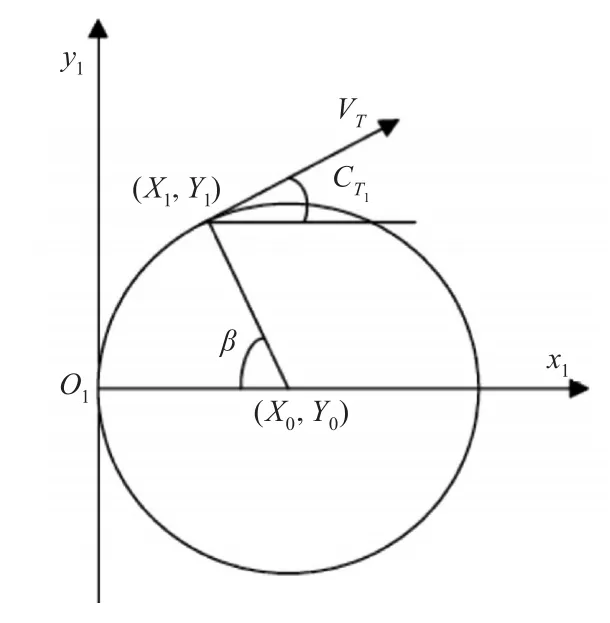
图2 环形弹道模型

环形弹道半径Rat=Vt/ωT，环形弹道圆心(-ωT∙Rat,0,Zc)，鱼雷在t1时刻的回旋角度为β=ωT(t1-tc)，鱼雷在t1时刻在鱼雷坐标系中的坐标和航向为

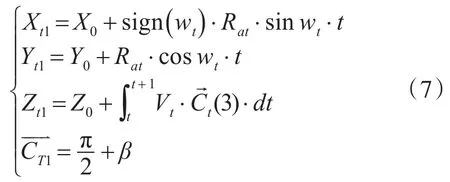
相应可得t1时刻鱼雷在地理坐标系中的位置(X,Y,Z)：

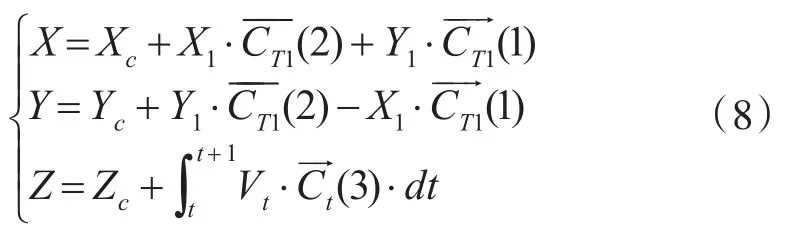
2.3 空投鱼雷散布误差

空投鱼雷对潜攻击时，火控系统根据声呐反馈到的目标信息解算投雷点，由于影响投雷的因素较多如：降落伞参数、投放条件、火控系统、声呐定位等，这些条件在整个复杂的投雷过程中均会存在误差，故空投鱼雷落点存在误差［5］。图3是以400m高度，200km/h速度前飞投雷时的投雷误差散点图。

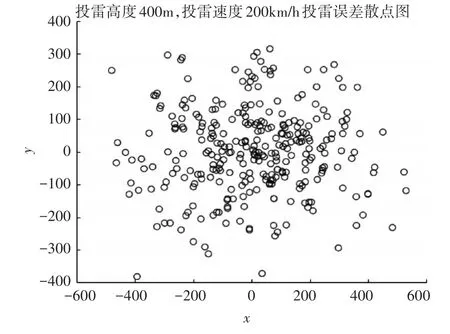
图3 空投鱼雷散布点图

根据已有的研究可得，空投鱼雷误差服从正态分布，并且落点误差可分解为与航向平行、垂直两个方向并且相互独立。由投雷误差经验公式可得，鱼雷在雷体坐标系中x轴方向（平行于鱼雷航向）和y轴方向（垂直于鱼雷航向）的散布均偏差分别为［6］

式中：H为反潜机投雷时的飞行高度，V为反潜机投雷时的飞行速度。图4、图5为航速0～400km/h，飞行高度10m～500m情况下x方向和y方向上的投雷误差。

图4 空投鱼雷x方向上散布趋势

图5 空投鱼雷y方向上散布趋势

由正态分布定义可得概率偏差和均方差的关系如下：

又因ρ≈0.4769［7］，可得：

投雷偏差数据适用于雷体坐标系中，在实际作战使用时，需要将坐标系变换到地理坐标系中。故需要将投雷误差进行转换，可得下式：

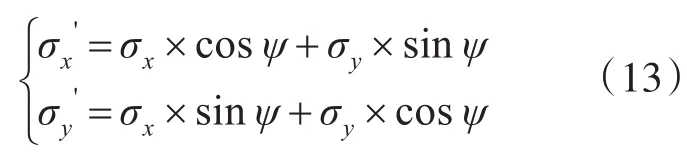
3 反潜鱼雷声自导模型

声呐方程分为主动声呐方程和被动声呐方程，主动声呐方程又分为噪声掩蔽下和混响掩蔽下的声呐方程［8］。本文主要考虑噪声条件下搜捕情况。噪声掩蔽下的声呐方程为

将鱼雷的各项参数带入声呐方程中，可准确计算鱼雷主动自导作用距离，但在实际研究中自导发射声源级SL（dB）、自导接收指向性指数DI（dB）、检测阈DT（dB）的参数获得十分困难，在现有情况下，利用有限的数据进行较为准确的仿真是我们研究的重点。

3.1 传播损失

为简化传播损失的描述，通常用球面扩展加吸收损失对传播损失进行估算［9］。即：

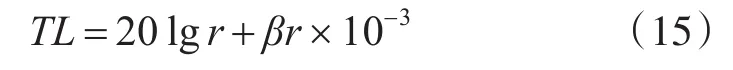
式中TL为传播损失（dB）；r为传播距离（m）；β为对数吸声系数（dB/km）。

常用的声吸收系数估算公式有：

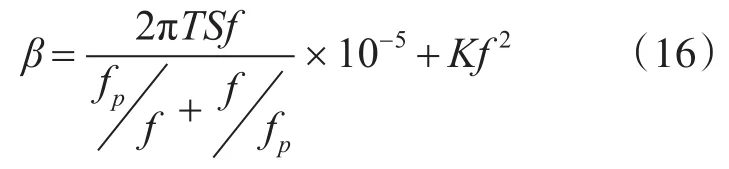
式中：f为声波频率（kHz）；T为海水温度（°K）；S为每千克海水中盐的总重量（g），成为海水盐度；为弛豫频率（kHz）：

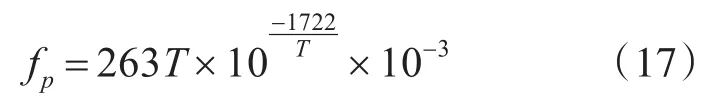
k为与海水温度有关的系数：

上式较为全面地反映声吸收系数的影响因素。对现役鱼雷一般可取β=4dB/km～8dB/km计算［10］。

3.2 目标反射强度

物体的目标反射强度不是定值，与物体的反射面积等诸多因素有关。在实际作战中实测潜艇目标强度是与声呐发出声波探测到潜艇时潜艇的反射面积决定的，即可转换为潜艇航向角和鱼雷航向角的夹角构成的函数［11］，即：

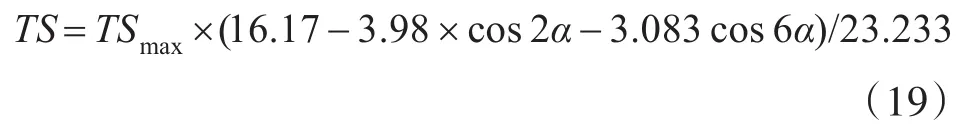
TSmax为最大反射强度，通常情况下潜艇横向反射强度最大，艇首和艇尾最小。α为潜艇航向与鱼雷航向夹角。

3.3 鱼雷干扰噪声级

声自导鱼雷的干扰噪声来源主要是由鱼雷航行的自噪声和海洋环境噪声共同组成。但通常情况下鱼雷自噪声级远大于海洋噪声级，故本文只考虑鱼雷自噪声［12］。

4 主动自导检测模型

声呐方程是判定主动声自导系统的依据，声呐方程将声信号的强弱与距离、角度构成联系，方便在仿真中进行检测。

4.1 求解自导作用距离

若目标在鱼雷的自导搜索角度范围内，在发现目标时记目标航向与鱼雷航向的夹角为Q。进一步可求得目标强度TS。将鱼雷参数SL、NL、DI、DT带入式（14）可得传播损失TL，从而得到自导作用距离r。由鱼雷、潜艇坐标求得两者距离D，通过比较r、D的大小即可判断鱼雷是否搜捕到目标［13］。

4.2 求解回声级

式（14）中NL-DI+DT项称为噪声掩蔽级，它是声自导装置在给定条件下能发现的最小信号级。SL-2TL+TS是换能器实际收到的信号强度，称为回声信号级。根据鱼雷、潜艇的航向，求得潜艇航向相对鱼雷航向的夹角Q，继而可求TS。再由潜艇与鱼雷的距离D，求得TL。代入SL-2TL+TS中可求得该条件下的回声级。如果SL-2TL+TS≥NL-DI+DT则捕获目标；反之为搜索到目标［14］。

4.3 声呐方程的简化使用

上述两种方法需要求得SL、DI、DT等参数，但实际情况很难获得真实的装备数据。为了仿真的真实性，需要对式（14）进行变形。根据式（14）可知在仿真过程中只有TS和TL是随潜艇、鱼雷的航向、位置在不断变化的，SL、DI、DT是基本不变的，将变量右移，常量左移得：

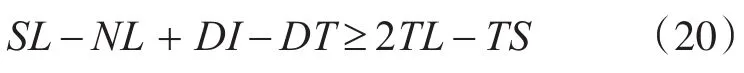
式（20）中不等式右边是声自导系统能探测到目标时最大的能量损失值，可将其作为定值，即令：

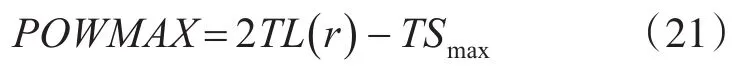
在仿真中任一时刻根据鱼雷到目标的距离D和鱼雷潜艇的航向夹角，求得TS和TL值，令

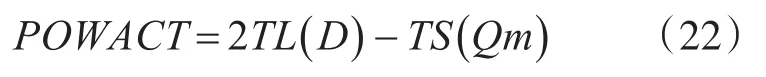
可求得任一时刻的损失的能力。然后判断是否满足POWACT≤POWMAX，即只要该值小于最大能量损失允许值，则认为声呐主动检测到目标，反之声呐探测不到目标。

通过式（20～22）可以在没有详细鱼雷自导系统参数的情况下，而根据TSmax对应的检测距离r为条件建立目标检测模型，该方法能真实反映自导系统的搜捕能力［15］。

5 仿真模型

5.1 仿真条件

本文对空投鱼雷对潜搜捕概率模拟原则如下：

1）反潜模式为应召反潜，反潜机接到目标位置信息后飞抵预定点位进行投雷，鱼雷初始航向为潜艇当前点位。投雷速度0～300km/h，投雷高度50m～300m；

2）鱼雷采用主动声自导，环形搜索模式；

3）本文只考虑搜捕概率，即只要鱼雷探测到潜艇即认为搜捕成功；

4）由于潜艇探测到鱼雷采取机动需要一定反应时间，而本文只考虑鱼雷探测概率，不涉及后续跟踪，故为简化模型，定义潜艇沿地理坐标系中的x轴正向做匀速直线运动。

5.2 雷、艇相对弦角、距离计算模型

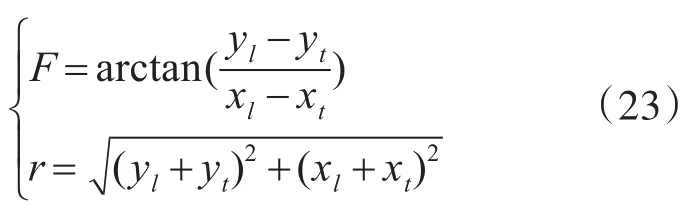
上式中，F、r为鱼雷相对于潜艇的弦角、距离；xl、yl为鱼雷坐标；xt、yt为潜艇坐标。

5.3 仿真参数

仿真参数如表1所示。

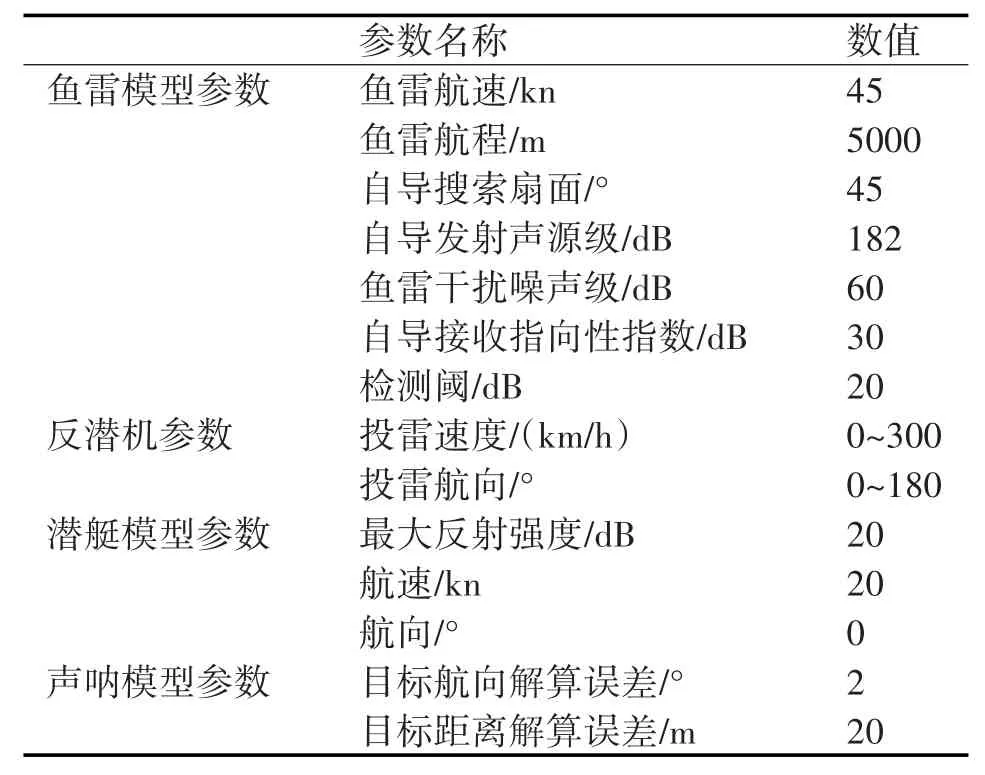
表1 仿真参数

6 仿真结果

反潜机以20m高度、200km/h投雷，因仿真模型具有的对称性，故只考虑反潜机从潜艇一侧投雷的情况，即鱼雷与潜艇弦角在0°～180°之间每间隔10°取一点，投雷距离1100m～2100m时每间隔200m取一点，每点仿真2000次，得鱼雷命中概率如图6。

图6 仿真图形

由图6可知在鱼雷自导性能确定的情况下，投雷距离越近，命中概率越高；在投雷距离大于1500m时，以45°和135°弦角投雷时鱼雷搜索到目标的概率高于其他角度的搜索概率，在投雷距离小于1500m时，以0°、90°、180°投雷时鱼雷搜索到目标的概率高于其他角度的搜索概率。

7 结语

通过分析鱼雷的落点散布误差模型、鱼雷水下环形搜捕运动模型、声自导检测模型，结合蒙特卡洛法仿真得到如下结论：在实际作战中，应尽可能靠近潜艇位置进行投雷，以期获得较高的命中概率。在投雷距离小于1500m时，应优先选择0°、90°、180°进行投雷，来获得较高命中概率；在投雷距离大于1500m时，应优先选择45°、135°进行投雷，来获得较高的命中概率。