一道平衡问题的多角度分析

谢汝成

(吉林省辽源市第五中学 136200)

题目如图1所示，一个半球形的碗放在桌面上，碗口水平，O是球心，碗的内表面光滑．一根轻质杆的两端固定有两个小球，质量分别是m1、m2.当它们静止时，m1、m2与球心的连线跟水平面分别成60°、30°角，则两小球质量m1与m2的比值是( ).

图1 图2

解法一：正弦定理解法

当物体受到三个共点力平衡时，三个力可成一个闭合三角形，通过题干所给条件去寻找到各力夹角之间的关系，最后利用正弦定理列出各个力大小关系方程求解.

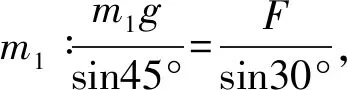
注：该方法作为处理平衡问题的基本办法之一，思维方法学生易于理解，计算相对简单，是解决三力平衡问题的常用解法.

解法二：相似三角形解法

相似三角形解法就是构建一个物体受力闭合三角形和另外一个相似的几何三角形，在两个三角形对应边比例一定的情况下，通过分析几何三角形的边长即可求解或判断出对应力的大小和大小的变化.

解析对物体受力分析，并分别做出两物体受力平衡三角形，如图3所示，取两小球所在位置为A点和B点，过圆心O向AB做竖直线，交AB于C点.此时不难发现：

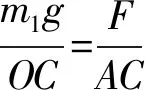
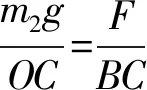
图3 图4

为计算两端线段长度的比例关系，如图4所示，过B点向OC做垂线并交于D点，过A点向OC做垂线并交于OC延长线上的E点

在△OBD中BD=Rsin60°

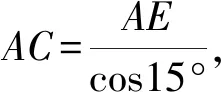
以上各式联立可得

注：大部分学生对相似三角形解法的认识通常停留在分析动态平衡问题中各力大小变化情况阶段，教师可以通过此题向学生强调相似三角形解法的更深入的应用，在某些复杂的力学平衡问题中可以将复杂的物理情景转化为一般数学运算，降低思维难度.

解法三：转动平衡解法

当物体在非共点力作用下保持静止或绕轴匀速转动状时，物体处于转动平衡状态，即力矩平衡.一般规定逆时针力矩为正力矩，顺时针力矩为负力矩.当物体处于转动平衡时各力矩的代数和为零，即M1+M2+M3+…+Mn=0

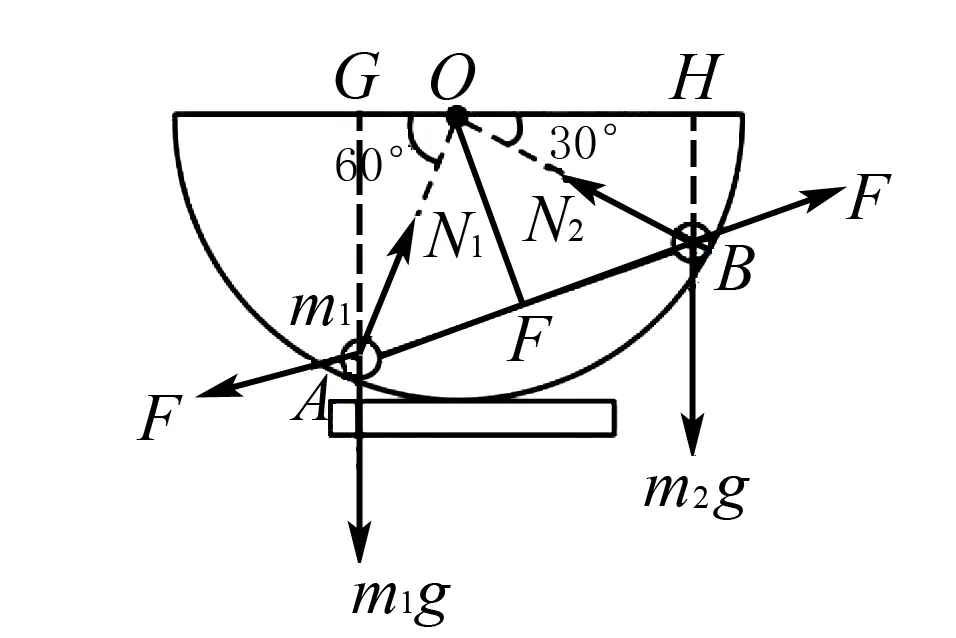
图5

解析由m1与m2两小球组成的系统在非共点力作用下静止，处于转动平衡.如图5所示，以O点为转动中心,过O点做AB的垂线OF,OF即是力F到转动中心O的距离,分别过AB两点做水平直径的垂线AG和BH,OG和OH分别是m1g和m2g到转动中心O的距离.

列转动平衡方程

F·OF+m1gOG-F·OF-m2gOH=0

其中OG=Rcos60°,OH=Rcos30°

注：转动平衡虽然在高考中不做考察，但学生在初中阶段已经经历了较为系统的学习，对此类知识较为熟悉.可以利用此种解法向学生展示初高中物理知识的衔接，同时作为拓展知识能使学生加深对共点力平衡问题的理解.

解法四：势能函数解法

对于保守力学系统，如果处于平衡状态，则系统总势能处于极值状态(稳定平衡时系统势能为极小值，似稳平衡时系统势能为极大值)，即系统势能的一阶导数等于零.

解析选经过O点的水平直径为重力势能零点，如图6所示.

Ep=-m1gy1-m2gy2

y1=Rsinθ，y2=Rcosθ

对Ep关于θ求导

图6

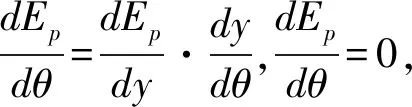
二是正确的写出系统的势能函数以及计算出势函数的一阶导数.

解法五：元功法

对于一个处于静态平衡状态的系统，可使它发生一段微小位移(元位移)，则系统所受的所有力在这个位移上所做微小总功(元功)之和零.

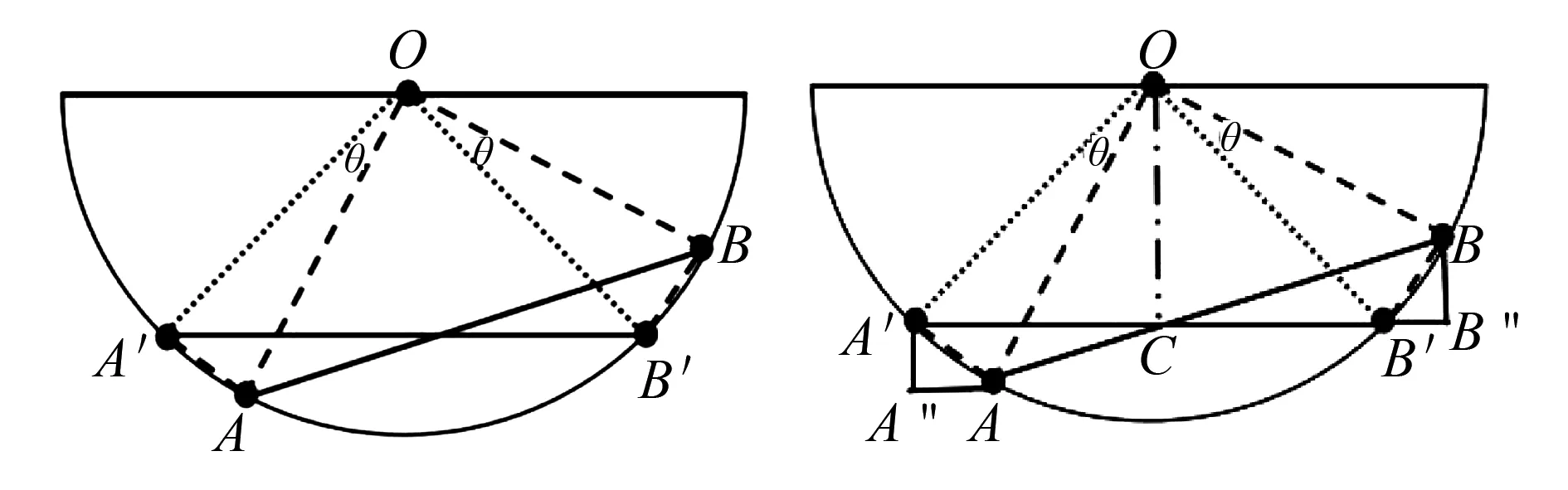
图7 图8

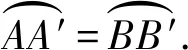
再过B′和B做水平和竖直线，交于B″点.在直角△BB′B″中,∠B′BB″=∠AOC=30°,BB″=BB′cos30°.

根据功能关系有：

m2gBB″-m1gA′A″=0,

注：元功法是以功能原理为依据的一类解决物理问题的方法，该种解法关键在于元位移的表达，是分析力学中的“虚功原理”的简单应用.用元功法在处理某些平衡问题时颇为简单．在使用元功法时，一般遵循一下四个步骤：

1.元过程的选取：取一与原平衡状态接近的另一状态，构造一个元过程

2.元位移的计算：利用微元法或极限法计算出系统内各物体的元位移

3.列方程：该元过程中所有力的元功之和为零

4.代入数据求解

该解法在计算元位移时也可以采用微分的方式

两小球到圆心的竖直距离分别为y1和y2(如图9所示)，假设OA向上转动一小角度θ，在θ→0的条件小球的竖直位移等于竖直坐标的微分.

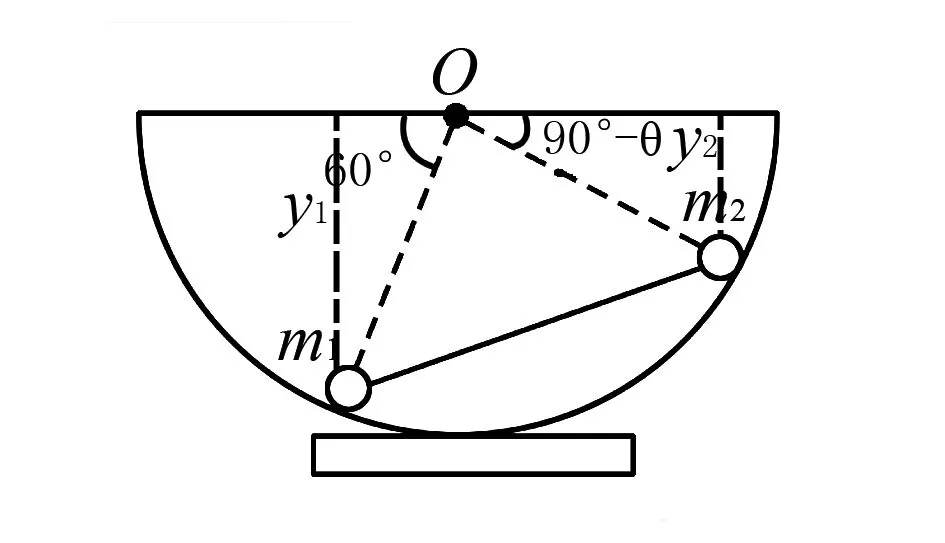
图9

y1=Rsin60°，δy1=Rcos60°dθ

y2=-Rcos30°，δy2=Rcos30°dθ，再利用W=m2gδy1+m2gδy2=0即可求解

综上所述，在实际的教学过程中，教师应该引导学生从更高的维度上多角度的分析问题，使不同能力的学生都能在一道题的讲解过程中提升自身的分析和解决问题的能力，这样才能帮助学生在有限的时间内更快更好的建立起物理学的知识体系，从容的面对各种各样的物理问题.