UNDERSTANDING SCHUBERT’S BOOK (II)*
2022-03-12BangheLI李邦河
Banghe LI (李邦河)
KLMM,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China E-mail:libh@amss.ac.cn
Abstract In this paper,we give rigorous justification of the ideas put forward in§20,Chapter 4 of Schubert’s book;a section that deals with the enumeration of conics in space.In that section,Schubert introduced two degenerate conditions about conics,i.e.,the double line and the two intersection lines.Using these two degenerate conditions,he obtained all relations regarding the following three conditions:conics whose planes pass through a given point,conics intersecting with a given line,and conics which are tangent to a given plane.We use the language of blow-ups to rigorously treat the two degenerate conditions and prove all formulas about degenerate conditions stemming from Schubert’s idea.
Key words Hilbert Problem 15;enumeration geometry;blow-up
1 Introduction
This paper is the sequel to[1].Here,we give rigorous justification of almost all of the formulas in§20,Chapter 4 of Schubert’s book[2].
In modern language,Schubert actually introduced linear combinations with rational coeffi-cients of subvarieties on a given variety,as well as the addition and multiplication of them under the numerical equivalence.To get the generators under addition and multiplication and the relation between generators,Schubert used the method of reducing to degenerate cases which was first introduced by Chasles and Zeuthen.
The method of reducing to degenerate cases is one of the key elements of Schubert’s success.Actually,when he used this method,he must have imagined that ordinary geometric objects were approaching degenerate objects in finitely closely.In his book,Schubert often used the language of in finite closeness,e.g.,two points that are in finitely close to each other and two lines that are in finitely close to each other.In the era of Schubert,however,the use of∈-δ language had replaced the use of the language of in finite closeness in analysis.Perhaps Schubert noticed the lack of rigor of the language of in finite closeness,so for conics that are in finitely close to a double line,he used a kind of projection to say that this kind of conic is a double line with two special points.This indeed avoided the use of the terminology of in finite closeness,but it was actually more difficult to understand.In our opinion,it is less rigorous than before.
To rigorously understand Schubert’s idea,we should use nonstandard analysis.In[3],we made a preliminary attempt to use nonstandard analysis.
For the case of conics,we can use blow-ups to avoid the language of nonstandard analysis.
In Section§20,Schubert studied conics in space.He introduced the following conditions:
1.μ:conics whose planes pass through a given point;
2.ν:conics intersecting with a given line;
3.ϱ:conics which are tangent to a given plane.
Schubert wanted to calculate all μmνnϱlwith m,n,l≥0,m+n+l=8,and for this,he introduced two invariant conditions or degenerate conditions:
1.η:those degenerate conics each having points forming a double line,and tangent lines forming two sets,each consisting of lines in a plane through a special point on the double line;
2.δ:those degenerate conics formed by two lines in a plane with all tangent lines being a double set consisting of lines in the plane through the intersection point of these two lines.
The strategy of Schubert to enumerate the numbers of required conics was to enumerate the relevant degenerate conics,i.e.,those satisfying the conditions η or δ.To do this,he needed to establish the following two equations concerning μ,ν,ϱ and η,δ:
1)η=2ν-ϱ-2μ;
2)δ=2ϱ-μ.
For the proof of these two formulas,Schubert merely said:
“We count the next two numbers for a one-dimensional system of conics:
·the first is the number of lines in a plane passing through one point that meet two points of a conic in the system;
·the second is the number of planes among all planes passing through a given line which possess two tangent lines of a conic in the system.
Then according to the correspondence principle,we get
ν+ν=ϱ+2μ+η
and
ϱ+ϱ=ν+δ.”
Next,Schubert gave the following two important observations:
“If the double line of a conic η intersects with a given line,then η may be thought as two conics satisfying the condition ν,because this given line has two common coincidence points with η.From this,the condition ηνnis 2ntimes of the following condition.This condition means that a conic will degenerate to η,whose double line intersects with n given lines.Similarly,the condition δϱγis 2γtimes of the following condition.This condition means a conic should degenerate to δ,whose double point sits on γ given plane.”
Then,Schubert gave three examples (i.e.,ημν2ρ4,δμ3ν3ρ2,and δν6ρ) to indicate the method he used to calculate the degenerated numbers with the application of the observations mentioned as above.In the calculation of δν6ρ,he also used the equation 15) between the basic conditions of the three principal elements in§6 of[2],which was proved rigorously in[1]to simplify the counting process.Finally,he gave two tables which listed all the relevant numbers.
RemarkThe application of the equation 15) between the basic conditions of three principal elements in the presently discussed work of Schubert was noticed by Bo Li and initially overlooked by the present author.
In this paper,we give the complete proof of these two tables following Schubert’s idea.Thus,the relation of μ,ν,and ρ is fully understood.
In modern language,we see that Schubert was working on the complete conic space,which is actually the blow-up of the CP5-bundle over the dual CP3,whose fiber is the set of quadratic forms on a plane in CP3,along the subvariety formed by the double lines.Here,we use C to denote the CP5-bundle over the dual CP3,andto denote the blow-up.For the case of plane conics,this was explained clearly by Kleiman in[4](p.470).Let

be the natural projection.
In this paper,we also use Ritt-Wu method[5]and the command“Rational Univariate Representation”in Maple to calculate the multiplicities of zero systems.Note that not all systems can be calculated by this command.Here is an example from[6]that the higher Tor cannot be ignored:given two ideals
I=(x1,x2)∩(x3,x4),I′=(x1-x3,x2-x4)
in C[x1,x2,x3,x4],denote W=V (I) and W′=V (I′) in C4.Then W∩W′is just the origin of C4,and the intersection number of W and W′is 2.However,the first term of Serre’s formula[7]is 3.We used the command“Rational Univariate Representation”in Maple to get the number 3.In spite of this,Grayson[8]indicates that if all the conditions come from cycles that are local complete intersections in smooth varieties,the higher Tor would disappear.In the application below,all we considered were complete intersections.Thus,we can use the command“Rational Univariate Representation”to calculate the multiplicities.
We prove the formulas 1) and 2) in Section 2.In Section 3,we give the proof of Schubert’s two observations.In Sections 4 and 5,we check all the numbers in the two tables of Schubert.
2 Proofs of formulas 1) and 2)
We prove these along the lines Schubert’s idea,as was mentioned in the introduction.
Proof of the formula 1)First,we take an affine open subset U of C.Let vu+gx+hy+iz=0 be a plane in CP3={[u,x,y,z]},and[v,g,h,i]be a coordinate of the dual space of CP3.For the plane for which v0,the quadratic curve on it can be represented by u+gx+hy+iz=0 and ax2+by2+cz2+2dxy+2exz+2fyz=0.Let U be the set of the above quadratic curves with a=1;this is a Zariski open set of C isomorphic to C8with parameters (g,h,i,b,c,d,e,f).For any quadratic curve represented by a point in U,if it intersects the line x=a1t,y=a2t,z=1 with parameter t and[a1,a2]∈CP1in the plane u=0,when t is finite,the intersection point is determined by the following two equations:
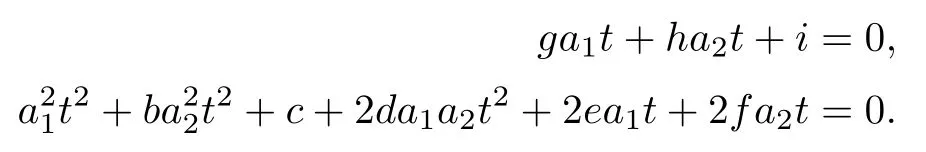
When t is in finite,the conic intersects the plane u=0 at in finity and the closure of all these conics form a seven dimensional subvariety.For the case in which t is finite,we may eliminate t to get

For t being in finite,this equation must also hold.
If all the three coefficients i2+cg2-2eig,2(cgh+di2-eih-fig) and bi2+ch2-2fih are zero,then all[a1,a2]∈CP1are solutions of equation (2.1).There are three cases.In Case 1,the conic passes through the origin of the plane u=0,which is equivalent to i=c=0.In Case 2,the conic lies on the plane u=0 which is equivalent to g=h=i=0.In Case 3,the conic is actually two intersection lines and one of the lines lies on the plane u=0.All of these conics represented by points in U form a Zariski closed set with dimension 6 or 5.Thus,the dimension of the closure of their strict transformation in the blow-up space is not greater than 6.
If the coefficients are not all zero,equation (2.1) must have two solutions:[a1,a2],[].If the two solutions are the same,there are two cases.In Case 1,the conic represented by a point in U intersects the plane u=0 at two points on the same line passing through the origin.In Case 2,the conic intersects the plane u=0 at a double point.The two solutions are the same if and only if

which is factored to
-4i2H=0,
where
H=(b-d2) i2+(c-e2) h2+(cb-f2) g2+2(de-f) ih+2(df-eb) ig+2(ef-cd) gh.
i=0 is obviously the equation for the conics whose planes pass through the origin.We claim that H=0 is the equation for conics that intersect with the plane u=0 at a double point.Let u+gx+hy+iz=0 be the plane of a conic whose projection on the plane u=0 is given by
x2+by2+cz2+2dxy+2exz+2fyz=0.
Then its intersection with the plane u=0 is given by

(h2-2dgh+bg2) y2+2(fg2+ih-egh-dig) yz+(i2-2eig+cg2) z2=0.
If the three coefficients of the equation are all zero,the plane u=0 contains in finite points of the conic.In this case,the conic must be tangent to the plane u=0.If the coefficients are not all zero,the conic intersects with the plane u=0 at a double point if and only if
(fg2+ih-egh-dig)2-(h2-2dgh+bg2)(i2-2eig+cg2)=0,
which is factored to-4g2H=0.This shows that for g0,H=0 is the equation for intersecting at double points or tangent to the plane u=0.Then,by the closeness of the condition,this also holds for g=0.The claim is proven.
To give an affine coordinate system over U,we first change the coordinate of U to a new coordinate system (g,h,i,d,e,u,v,w) such that b=u+d2,c=v+e2,f=w+de,g=g,h=h,i=i,d=d,e=e.In the new system,the set of double lines is given by
u=v=w=0.
This can be proven as follows:if the conic x2+by2+cz2+2dxy+2exz+2fyz=0 represents a double line,it must have the form (x+dy+ez)2=0.Comparing the coefficient of every monomial,we can get that
b-d2=0,
f-de=0,
c-e2=0,
which is the same as u=v=w=0.The blow-up π-1(U) of U is covered by three affine spaces.One of them is given by the coordinates (g,h,i,d,e,w,k1,k2)∈C8,where
k1=u/w,k2=v/w
In the above coordinate system of π-1(U),equation (2.2) pulled back by π is given by

where

Since η is given by w=0,when w0,=0 implies that the corresponding conic is tangent to the plane u=0.The element in η is in fact a straight line with two special points and any straight line in the plane containing this conic that passes through one of these two points is tangent to this conic.If=0 and w=0,one of the points of the element in η must be on the plane u=0.The plane that contains the conic in η intersects the plane u=0 at one straight line.This straight line must be the tangent line of this conic.Therefore,in the case=0 and w=0,the conic is tangent to the plane u=0 at a double point.Thus,the closure of=0 inrepresents the condition ϱ.
Note that the closure of i=0 inrepresents the condition μ,and the closure of w=0 inis the condition η.Here the closure is under the Zariski topology.
For any one dimension cycle,by Chow’s moving lemma[10-12],we may assume that there is an irreducible curve γ which intersects properly with the following cycles:
1) the cycle given by the closure inof the inverse image under π of all the points in U in which all three coefficients i2+cg2-2eig,bi2+ch2-2fih and 2(cgh+di2-eih-fig) are zero,which has at most six dimensions;
3) the cycle given by the closure of the set given by the equation i=0 in,which has seven dimensions;
4) the cycle given by the closure of the set given by the equation w=0 in,which has seven dimensions;
5) the cycle given by the closure of the set given by the equation,which has seven dimensions;
6) the cycle generated by the closure inof the set given by the equation i=0 minus,which has six dimensions;
7) the cycle generated by the closure inof the set given by the equation w=0 minus,which has six dimensions;
8) the cycle generated by the closure inof the set given by the equation=0 minus,which has six dimensions;
9) the cycle given by elements inwith its image under π intersecting with the in finity line of the plane u=0 with x,y coordinates,which has seven dimensions.
Let α1=i2+cg2-2eig,α2=2(cgh+di2-eih-fig),and α3=bi2+ch2-2fih be polynomials of g,h,i,b,c,d,e,f.[α1,α2,α3]is a point in CP2.For any s∈γ,if π(s)∈U,then we can de fine (g (s),h (s),···,e (s),f (s)) as the coordinate of π(s) in U.Because of 1) and 2),except for finite points in γ,we can de fine a map from γ to CP2.Moreover,for 9),except for finite points,the conics de fined by points in π(γ) will not intersect the plane u=0 at in finity.Thus,the solution of (2.1) is well de fined except for finite points.

then one of the intersection points of the conic represented byand the plane u=0 is x=a1t,y=a2t for some t,and when t is in finite,it must be a point on the in finity line.
We prove that the image of α cannot be a single point in CP2.If this is the case,all the intersection points between the conics represented by elements in γ and the plane u=0 must be on only one or two straight lines passing through the origin.All these intersection points form an algebraic set.If this set is of dimension one,it must contain at least one of these straight lines.Then all the points on this line must be an intersection point.Therefore,some conics pass through the origin,but this is impossible because γ intersects properly with 1),as stated above.If the algebraic set is of dimension zero,it should be a pair of points.If this pair of points coincides,according to 2),except for finite elements in γ,they are inand satisfy either w=0 or=0.As γ intersects properly with 4) and 5) as stated above,there are only finite elements in γ that satisfy w=0 or=0;this leads to a contradiction.The pair of points cannot coincide.Every conic must intersect the plane u=0 at the same pair of two different points.Then all conics are contained in planes including the straight line that connects these two points,so the set of the planes that contain a conic in γ can be either all the planes passing through this straight line or a set of one single plane.In the first case,one of the conics in γ must stay in the plane u=0,which is excluded by the requirement that γ intersects properly with 1),as stated above.In the second case,all elements of γ are included in a single plane.Then the set of the points in this plane which are passed through by some conics in γ is the whole plane,cf.[3],Section 2.1.Thus,taking one point on that straight line that is different from that pair of points,they must be on a curve in γ.Since this curve is a quadratic curve which contains three different points on a line,it must contain the whole line,which,again by 1),is impossible.
Now we de fine a morphism β:CP1×CP1→CP2as
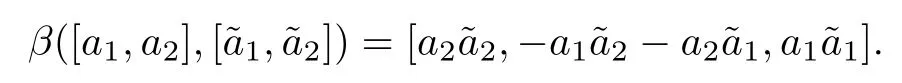
We assume that γ′is a curve of degree m in CP2which has the following equation:

Thus,β-1(γ′) has the form
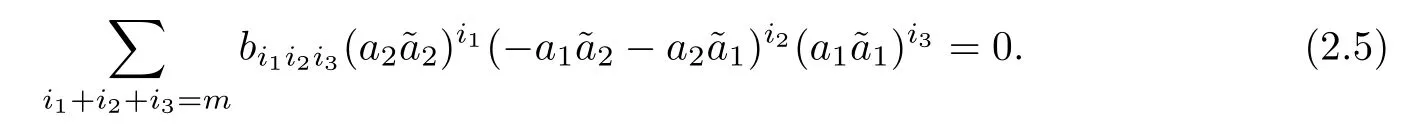
This equation is homogeneous with a degree m for both the variables a1,a2and.
Because of 3),4) and 5),the image of the intersection of β-1(γ′) and the diagonal under p1is finite.The set of singular points on γ′is finite,which is denoted by S.The set α-1(S) onis also finite.The restriction of α onα-1(S) is a k sheets branched covering.The ramification points of the branched covering are finite,so the images of these points[a1(s),a2(s)]are finite too.Furthermore,there are only finite s∈such thatU oris a singular point on γ,so the corresponding images[a1(s),a2(s)]are finite too.Also,there are at most finite points in CP1such that their inverse under p1intersects with β-1(γ′) at in finite points or at less than m points.Therefore,we can choose[a10,a20],which are not points stated as above,and we have a100,a200.
Let s0be such an element inwith[a1(s0),a2(s0)]=[a10,a20]and∈U.We may assume that a20=1.
Let l0be the straight line x=a10t,y=t,z=1 in the plane u=0.Forbeing a nonsingular point on γ,we may assume that s is itself a complex number around s0.All the conics represented by elements in U intersect with l0if and only if

where α1,α2,α3are polynomials of g,h,i,b,c,d,e,f.Thus,

is a function of s,g,h,i,b,c,d,e,f,and this function is equal to 0 at (s0,g (s0),h (s0),···,f (s0)).
Now we prove that

at (s0,g (s0),h (s0),···,f (s0)).According to the choice we have made for s0,
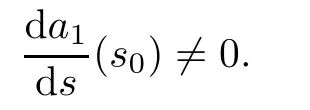
Thus,if

at (s0,g (s0),h (s0),···,f (s0)),it must be that
2a1α1+α2=0
at (s0,g (s0),h (s0),···,f (s0)).That is to say,
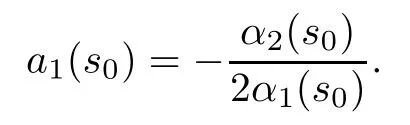
In this case,we must have that α2(s0)2-4α1(s0)α3(s0)=0,which contradicts the fact that β-1(α(s0)) is not on the diagonal.Therefore,0 at (s0,g (s0),h (s0),···,f (s0)).
Therefore,according to the implicit function theorem,there is a holomorphic function
s=S (g,h,i,b,c,d,e,f)
in a neighbourhood of (g (s0),h (s0),···,f (s0)) such that
F (S (g,h,i,b,c,d,e,f),g,h,i,b,c,d,e,f)=0,
and s0=S (g (s0),h (s0),i (s0),b (s0),c (s0),d (s0),e (s0),f (s0)).
Let H=s-S (g,h,i,b,c,d,e,f) be a function of g,h,i,b,c,d,e,f,s.As
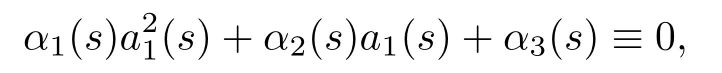
we have

in a neighbourhood of s0.Then,

in a neighbourhood of s0.Thus,among the terms in the above summation,there is at least one term not equal to zero at s0.Without loss of generality,we assume that

at s0.Then

at (g (s0),h (s0),···,f (s0)).Thus,

at (s0,g (s0),h (s0),···,f (s0)).
Therefore,according to the implicit function theorem,there is a holomorphic function
g=G (s,h,i,b,c,d,e,f)
in a neighbourhood of (s0,h (s0),···,f (s0)) such that
H (s,G (s,h,i,b,c,d,e,f),h,i,b,c,d,e,f)=0,
and G (s0,h (s0),i (s0),b (s0),c (s0),d (s0),e (s0),f (s0))=g (s0).
Given Φ:C8→C8,
Φ(s,h,i,b,c,d,e,f)=(G,h,i,b,c,d,e,f),
and given Ψ:C8→C8,
Ψ(g,h,i,b,c,d,e,f)=(S,h,i,b,c,d,e,f),
so we can easily verify that they are inverse mappings.We see that π(γ) under the transform Ψ can be represented by (s,h (s),i (s),b (s),c (s),d (s),e (s),f (s)).We recall the abuse of the notion s as a complex number or an element on.By this representation,we see that π(γ) is transverse at,with the subvariety determined by equation (2.6),which consists of conics that intersect l0.As π is biholomorphic near,γ is transversal at a representation of ν in.
Thus we see that,given[a1,a2]=[a10,a20],there are m solutions offor equation (2.5).Therefore,there are exactly km nonsingular elementsin γ such that[a1(si),a2(si)]=[a10,a20],i=0,···,km-1.
By Bezout’s theorem,γ′intersects with the curve-4α1α3=0 at 2m points,after counting multiplicities.Thus the total number of elements in γ with i2=0,=0 or w=0 is 2km after counting multiplicities.We can see that in γ the number of elements that satisfy ν+ν is equal to the number of elements that satisfy ϱ+2μ+η.Thus,the condition ν+ν is enumeratively equivalent to ϱ+2μ+η.That is exactly what Schubert meant by

Proof of the formula 2)According to Schubert’s hint,we prove formula 2) in what follows.As with the proof of formula 1),let u+gx+hy+iz=0 be a plane in CP3={[u,x,y,z]},and let x2+by2+cz2+2dxy+2exz+2fyz=0 be a quadratic curve on it.Then,U is de fined by all the parameters (g,h,i,b,c,d,e,f)∈C8.Moreover,the line g0is given by x=y=0.Then the planes passing through g0are given by gx+hy=0 or x=a1s,y=a2s with s as the parameter.The intersection of such a plane with a conic gives

Thus,they are tangent to each other if and only if

That is,

If the three coefficients e2-c,2(ef-cd),and f2-bc are zero,that means that all[a1,a2]∈CP1are solutions of equation (2.7).There are only two cases.In Case 1,the quadratic curve is a double line.In Case 2,the quadratic curve is two lines that intersect on the line g0.
For any one dimensional cycle,by Chow’s moving lemma we may assume that there is an irreducible curve γ which intersects properly with the following cycles:
1) the cycle given by the closure inof the inverse image under π of all the points in U that represent a double line,which is actually condition η that has seven dimensions;
2) the cycle given by the closure inof the inverse image under π of all the points in U that represent two intersecting lines with intersection point on g0,which has five dimensions;
Let α1=e2-c,α2=2(ef-cd),and α3=f2-bc be polynomials of b,c,d,e,f.[α1,α2,α3]is a point in CP2.For any s∈γ,if π(s)∈U,then we can de fine (g (s),h (s),···,e (s),f (s)) as the coordinate of π(s) in U.Because of requirements 1),2),and 3),except for finite points in γ,we can de fine a map from γ to CP2.
As with the proof of the first formula,letbe a nonsingular projective curve and let→γ be a morphism such that the restriction of(the set of singular points of γ) to γ he set of singular points of γ is an isomorphism.Therefore,except for finite points in,we can de fine a morphism fromto CP2that maps s∈to[α1(s),α2(s),α3(s)],which can be extended to a morphism α:→CP2.
Asking the equation (2.7) to have a double root for[a1,a2]∈CP1leads to
(c-e2)(cb-f2)-(dc-ef)2=0,
which is factored into cH=0,where
H=cb-f2-e2b-d2c+2def=0
is exactly the equation of all conics consisting of two lines in the present affine set.The closure of π-1({H=0})∩is exactly the condition δ,and δ∩has six dimensions.Letbe the closure of π-1({c=0}),which is exactly the set of all elements inwhose image under π represents a conic which intersects with g0.Then,has six dimensions.We further require that γ be proper to
5)δ∩η,which has six dimensions;
9)δ,which has seven dimensions.
Now,we consider the case in which the image of α is a single point in CP2;i.e.,for any s∈,equation (2.7) is the same one.If this equation has a double root for[a1,a2],then all elements in γ are in δ,which is impossible because of the requirement 9).If this equation has two different solutions,[a1,a2]and,then all the conics represented by elements in γ are tangent to the same two planes.Thus,all conics represented by elements in π(γ) would not be tangent to any other planes.Then the intersection number of ϱ and γ is zero.Because of the requirement 6),any elements in γ and δ must be in π-1(U).According to requirement 5),this element cannot be in η either.Because of the requirement 8),the conic represented by∈γ∩δ should not intersect g0.Thus,this conic has at most one plane which passes through g0and is tangent to it,which contradicts the stipulation that any elements in γ are tangent to two different planes containing g0.Therefore,the intersection number of δ and γ is zero.
Moreover,for the requirements 7) and 8),any conic that is represented by an elementin γ intersects with g0must be represented by elements in π-1(U)η.As we have proved thatcannot be in δ,the conic represented byis nonsingular and is tangent to only one plane passing through g0.This is a contradiction.Thus,the intersection number of ν and γ is zero.The formula
2ϱ=δ+ν
holds for such γ.
As in the proof of the first formula,we de fine the morphism β:CP1×CP1→CP2as

To guarantee that the two points of β-1(α(s)) coincide if and only if eitheris in δ oris in,we further require that γ is proper to
10) the set of all the elements inwhose planes pass through g0,which has six dimensions.
Because of the requirement 10),the plane of the conic represented by π(s),s∈γ intersects g0as a projective line at a single point.If the conic represented by π(s),s∈γ intersects with g0,the conic should not be a double line for the requirement 7),and for the requirement 8),the intersection point should not be the in finity point of g0.Now we consider the cases in which the two points of β-1(α(s)) coincide.In Case 1,the conic intersects with g0.For the requirement 2),the conic should not be two lines with intersection points on g0,so in this case the conic could be a nonsingular one which intersects with g0or two lines in which one of them intersects g0and the other one does not.In Case 2,the conic does not intersect with g0.If the conic is nonsingular,it must have two different tangent planes that pass through g0,so the conic must be singular,i.e.,in η or δ.For the requirement 5),the conic cannot be in η.Thus,in this case,the conic should be two different lines that do not intersect with g0.
The remaining proof is just like the proof of Schubert’s first formula.The image ofunder α is an irreducible curve denoted by γ′.The morphism fromto γ′is a k branch covering.
We then analyse β-1(γ′) as before,such that β-1(γ′) is homogeneous with degree m for both the variables a1,a2andrepresented by

Due to requirements 4) and 9),the intersection of β-1(γ′) and the diagonal is finite.Thus the image of this intersection under p1is finite.The set of singular points on γ′is finite,which is denoted by S.The set α-1(S) onis also finite.The restriction of α onα-1(S) is a k sheets branched covering.The ramification points of the restriction map of α are finite,so the images of these points[a1(s),a2(s)]are finite too.On account of requirement 3),there are only finite s∈such thatU.Also,there are only finite s∈such thatis a singular point on γ.Then the corresponding images[a1(s),a2(s)]are finite.There are at most finite points in CP1such that their inverse under p1intersects with β-1(γ′) at in finite points or at less than m points.Therefore,we can choose[a10,a20]which are not points stated above,and a100,a200,adding the extra requirement that[a10,a20],which is guaranteed by requirement 1).
Choose that x=a10s,y=a20s is a plane passing through g0.All the conics represented by elements in U are tangent to this plane if and only if

where α1,α2,α3are polynomials of g,h,i,b,c,d,e,f,as above.Denote

The closure of π-1(G)η represents the condition ϱ.
The fact that γ is transverse at a representation of ϱ incan be proved by the same procedure as in the proof of the first formula.Now we see that,given[a1,a2]=[a10,a20],there are m solutions offor equation (2.8),so the number of elements in γ satisfying the condition ϱ is exactly km.
Therefore,there are exactly km nonsingular elementsin γ such that[a1(si),a2(si)]=[a10,a20],i=0,···,km-1.
According to Bezout’s theorem,γ′intersects with the curve-4α1α3=0 at 2m points after counting multiplicities.We have proved that this happens if and only ifis in δ oris in.Furthermore,note that the restriction of π on π-1(U)η is biholomorphic.Thus we need only to consider the equation cH=0 in U.The total number of elements in γ with c=0 or H=0 is exactly 2km after counting multiplicities.We can see that in γ the number of elements that satisfy ϱ+ϱ is equal to the number of elements that satisfy δ+ν.This proves the formula for such γ.The proof is complete. □
3 Proofs of Schubert’s Observations
Two important observations of Schubert are as follows:
“If the double line of a conic η intersects with a given line,then η may be thought as two conics satisfying the condition ν,because this given line has two common coincidence points with η.From this,the condition ηνnis 2ntimes of the following condition.This condition means that a conic will degenerate to η,whose double line intersects with n given lines.Similarly,the condition δϱγis 2γtimes of the following condition.This condition means a conic should degenerate to δ,whose double point sits on γ given plane.”
At first glance,this is very difficult to understand,but Schubert was right,and we will give precise explanations and prove it.
Proof of the assertion aboutηνnAs before,take the affine open set of the CP5-bundle over CP3*with coordinates g,h,i,b,c,d,e,f.On the plane u+gx+hy+iz=0,a conic is given by
x2+by2+cz2+2dxy+2exz+2fyz=0.
Let g1,g2,g3,g4be the lines such that
g1:u=0,y=x;
g2:u=0,y=z;
g3:u=x,y=2x;
g4:u=x,y=2z.
Then the equation of conics passing through them are given by the following polynomials:
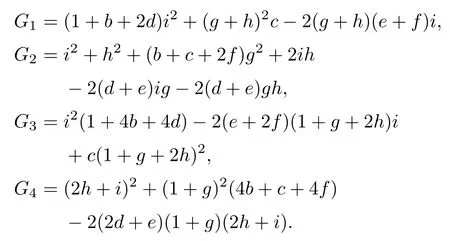
The two lines which intersect with the above four lines g1,g2,g3,g4,regarded as double lines with planes,are elements of U.As discussed above,the blow-up π-1(U) of U is covered by three affine spaces.Here we choose the one that is given by the coordinates (g,h,i,d,e,v,k1,k2)∈C8,where
k1=u/v,k2=w/v
The proper transformations of the hypersurfaces are given by the above polynomials G1,···,G4via the substitutions
c=v+e2,b=k1v+d2,f=k2v+de;
that is,they are given by the polynomials
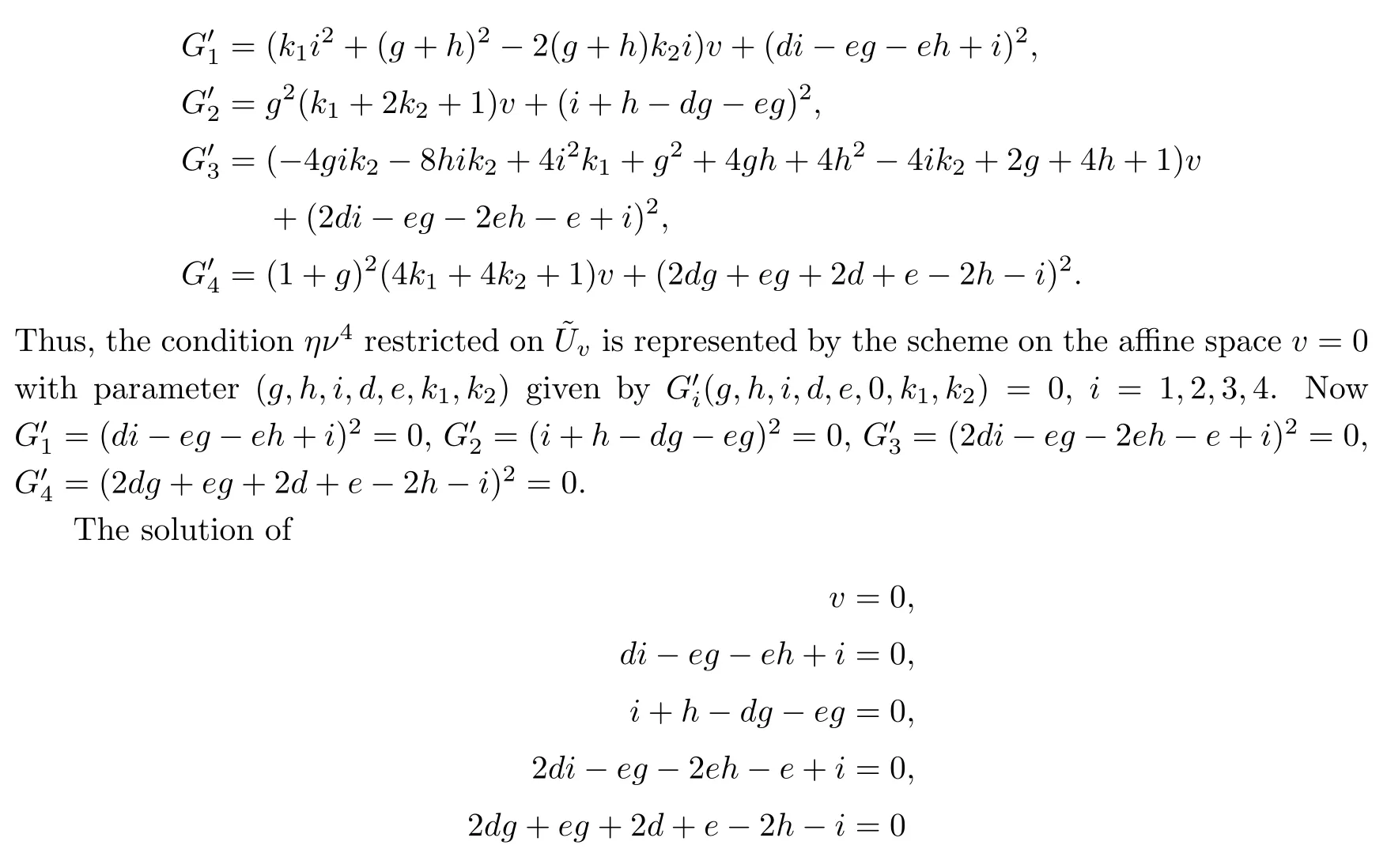
contains the following two components:
h=i=d=e=0,
and
i+g-1=0,h=-1,d=0,e=-1.
These are exactly the two lines that intersect with g1,g2,g3,g4,and are regarded as double lines with planes.These two one dimensional components×C2={(k1,k2)}amount to exactly“the following condition”in Schubert’s statement.To be more precise,we prove that each of these two components given by=0 is of multiplicity one.

where J1,···,J5are just the 4×4 sub-determinants of the Jacobian matrix
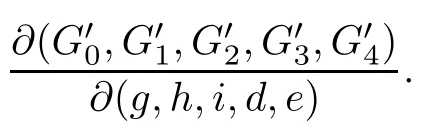
Thus,using the command‘wsolve’[5],
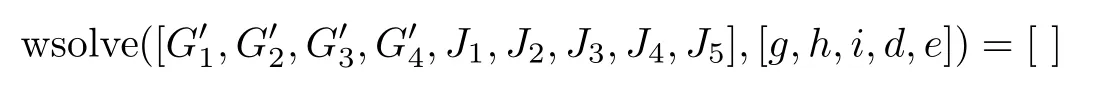
assures us that the intersection ofis transverse.The proof for n=4 is complete.
Proof of the assertion aboutδϱγIn U,we may choose three planes given by
x=0,y=0,and u=x.
The quadratic curves in the plane u+gx+hy+iz=0 are given by
x2+by2+cz2+2dxy+2exz+2fyz=0.
We have that a quadratic curve intersects with the plane x=0 at a double point if and only if bc-f2=0,and the same for the plane y=0 if and only if c-e2=0.
To see the equation for u=x,notice first that it intersects with the plane u+gx+hy+iz=0 at the line with a projection on a (x,y)-plane satisfying
(1+g) x+hy+iz=0.
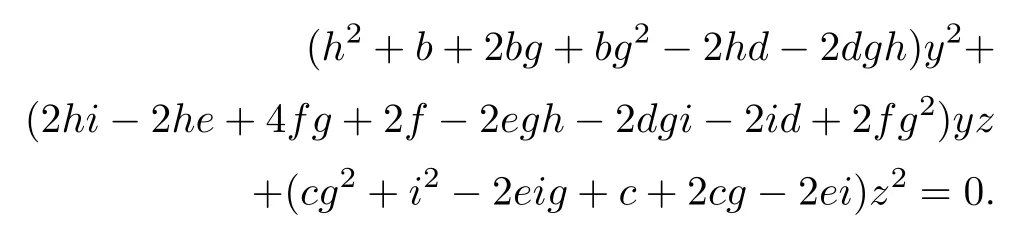
Asking this to have a double root leads to

Substituting b=u+d2,c=k1u+e2,and f=k2u+de into the equations
c-e2=0,bc-f2=0,K=0,
we obtain π-1for π restricted onfor the above equations,and
uK1=0,uK2=0,uK3=0,
where K1≜k1,K2≜(k1-) u+e2-2k2de+k1d2,and K3≜(1+g)2(k1-) u+((u-gd)2+d2+2gd2-2hd) k1+2(id-2gde-g2de+dgi+he-hi-de+egh) k2+(ge-i)2+e2+2ge2-2ei.Then,K1=0,K2=0,and K3=0 are just the equations of the strict transformations of c-e2=0,bc-f2=0,and K=0 in={(g,h,i,u,k1,k2,d,e,)}.
Now,the equation of δ in the projection to U is
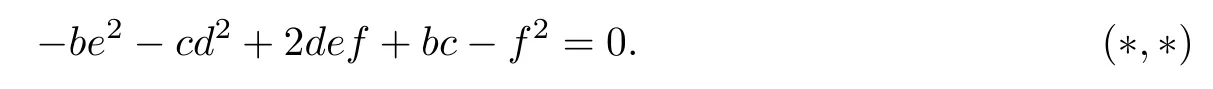
Substituting b=u+d2,c=k1u+e2,and f=k2u+de into (*,*),we obtain

Thus,the condition δ as the strict transformation of (*,*) is represented by
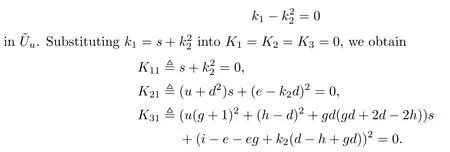
Now,in the new coordinated system (g,h,i,s,u,k2,d,e),δ is represented by
s=0.
Thus,the condition δϱ3restricted onis represented by the scheme on the affine space s=0 with parameter (g,h,i,u,k2,d,e),given by Ki1(g,h,i,0,u,k2,d,e)=0,i=1,2,3.Now K11==0,K21=(e-k2d)2=0,and K31=(i-e-eg+k2(d-h+gd))2=0.
The solution of

which is exactly the two lines that intersect at the origin with the planes.This is exactly“the following condition”in Schubert’s statement,and it is easy to see that the lines have multiplicity one.
The proof for γ=3 is complete;it is similar for γ=1,2. □
4 Formulas about Degenerate Conditions
The degenerate numbers are
δμmνnϱ7-m-nand ημmνnϱ7-m-n.
Schubert gave three examples (i.e.,ημν2ρ4,δμ3ν3ρ2,and δν6ρ) to indicate the method he used to calculate the degenerated numbers.
He calculated that ημν2ρ4=40 as follows:for the two special points on the line in η,we have to consider four planes determined by the condition ρ4and divide them into two groups.Each group determines one special point.There are two kinds of groupings.In the first we group three planes for the first group and the left one for the second group.There arecases in this kind of grouping.In the second one,each group of planes contains two planes.There arecases in this kind of grouping.For the first kind of grouping,the first special point should be the only intersection point of the three planes in the first group.The double line must be the unique line that passes through the first special point and the two lines determined by ν2.The second special point must be the only intersection point of the double line and the fourth plane in the second group.The double line should lay on the unique plane determined by the double line and the point determined by μ.For the second kind of grouping,the double line should intersect two general lines determined by ν2.Also,the double line should intersect with the line which is the intersection line of two planes in the first group and with the line which is the intersection of the two planes in the second group.There are only two lines that pass through four lines in general position.Thus,for the second kind of grouping,we can get two elements in η.Finally,note that all the numbers should be counted 22times as the first observation about the condition ην2.We get

solutions geometrically.
Schubert proved δμ2ν3ρ2=24 as follows:the condition δϱ2means that the double points of the elements of δ are on a line l1.Let g1,g2,g3be the 3 lines relevant to ν3.Let l2be the line such that μ2is represented by the plane passing through it.There are only two lines,d1,d2,that pass though the four lines g1,g2,l1,and l2.There is only one plane eithat passes through l2and di.The plane eiintersects g3with one point.Thus there are only two elements in δ in which one of the lines passes through g1,g2and the other passes through g3.Thus,=3 implies that there are 6 elements.
Schubert stated δν6ρ=140 as follows:δϱ implies that the double points of the elements of δ are on the plane Γ of ϱ.Four of the six lines determine the two lines intersecting with Γ at two points,each of which determines a line passing through it and the remaining two of the six.Thus any four give two elements of δν6ϱ.In this way,we get=30 elements.
The condition that a line passes through three lines is equivalent to two times the condition that a line lays on a given plane and passes through a given point.We could find

elements in this way.
These examples demonstrate Schubert’s genius.However,he only calculated the geometrical solutions.We have to use algebraic equations to check the multiplicities of these solutions.Schubert summarized his calculations in a table.Now we will check the degenerate numbers in this table case by case.The three examples in what follows are cases (42),(8),and (20).
(1)δμ3ν4=3.
μ3implies that the plane passes through three points in a general position,so there is only one such plane on which the quadratic curves lie.ν4implies four lines intersecting with the plane at four points in general position.Thus,the quadratic curve should pass through these four points.Then,no double line is possible.Divide the four points into two groups such that each group contains two points.There are just three methods for doing,each one contributing a quadratic curve in δ.Thus the total number in δ is three.This should be Schubert’s reasoning.To prove that each of the three solutions has a multiplicity of one,we choose the plane given by μ3to be u=0,and the quadratic curve in u to be given by
ax2+by2+cz2+2dxy+2exz+2fyz=0.
The equation of δ in u=0 is
abc-af2-be2-cd2+2def=0.
This is an equation of degree three.The quadratic curve passes through[x0,y0,z0]should satisfy the following equation:

This is a linear equation in CP5={[a,b,c,d,e,f]}.Thus the solutions of δμ3ν4are given by one equation of degree three and three equations of degree one.If there are only finite solutions,then by Bezout’s theorem,the number of solutions is three with multiplicity,so each solution by Schubert’s method must have multiplicity one.
(2)δμ3ν3ϱ=6.
Notice that we can use the second assertion of Schubert to say that δμ3ν3ϱ was twice the number of solutions geometrically satisfying δμ3ν3ϱ.μ3implies that the plane passes through three points in a general position,so there is only one such plane on which the quadratic curves lie.The plane given by ϱ intersects with this plane at a line.ν3implies three lines intersecting with the plane at three points in a general position.Thus,the quadratic curve should pass through these three points.Choose two of the three points.Connecting line of any two of the three points intersects with the line coming by ϱ at one point.Connecting this point with the other point of the three yields a line,which,together with the former line,yields an element in δ.Thus there are just three such elements in δ.
Then we have to give equations to show that all three of these solutions have a multiplicity of one.The process is a little bit complicated.
Let u=0 be the plane given by the condition μ3.This means all of the relevant quadratic curves in U satisfy
g=h=i=0.
Let y=0 be the plane giving the condition ϱ.Let[0,0,1,1],[0,0,-1,1],and[0,1,2,1]be the three points which are the intersections of the three lines coming from the condition ν3.The elements of δμ3ν3ϱ satisfy
x2+by2+cz2+2dxy+2exz+2fyz=0
on the plane u=0,so the equations of conics passing through the three points are given by

As we found before,the quadratic curve intersecting with the plane y=0 at a double point is given by
c-e2=0,
and the equation of δ in the projection to U is
-be2-cd2+2def+bc-f2=0.
Substituting b=u+d2,c=k1u+e2,f=k2u+de into the above equations,we obtain π-1for π restricted onfor the above equations:

Thus the condition δ as the strict transformation of-be2-cd2+2def+bc-f2=0 is represented by

Substituting k1=s+further into the above equations,we obtain

Now,in the new coordinate system (g,h,i,u,s,k2,d,e),δ is represented by
s=0.
Substituting s=0,we get

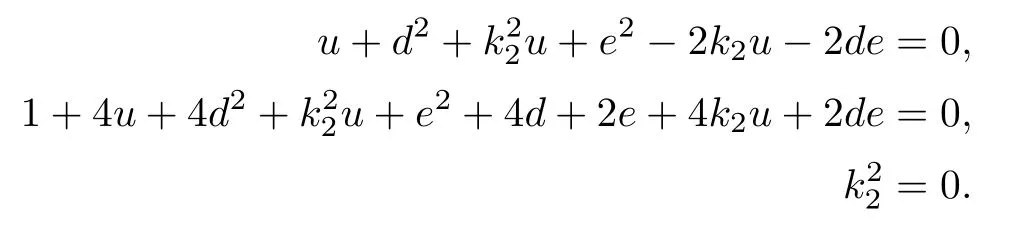
This shows that the number of solutions to the above equations is twice the number of the solutions to the following equations:

To solve these equations,we substitute k2=0 into other equations and get
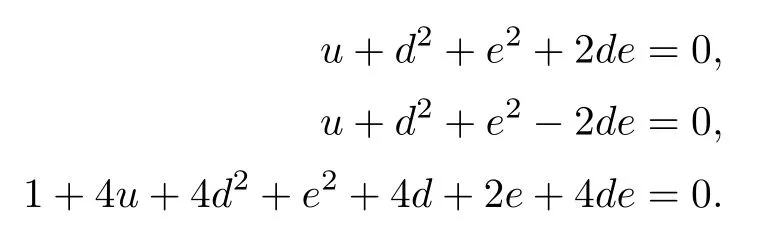
The third equation minus 4 times the first one is

and the first equation minus the second equation yields

(4.1) plus (4.2) yields
1-3e2+4d+2e=0.
Multiplying this by e then substracting (4.2) yields
e+2e2-3e3=0.
Thus we get a new basis of the ideal generated by the polynomials of the original equations;that is,
g,h,i,s,k2,e+2e2-3e3,1-3e2+2e+4d,d2+e2+2de+u.
From this,we see immediately that there are three solutions,each of which has multiplicity one.
(3)δμ3ν2ϱ2=4.
The second assertion said that δμ3ν2ϱ2is four times the number of solutions geometrically satisfying δμ3ν2ϱ2.μ3implies that elements of δ must be in a given plane.This plane intersects with the intersection of the two planes given by ϱ2at a single point.Then this point must be the double point of an element in δ which passes through the two points given by the intersection of the two lines representing ν2with the given plane.This is obviously unique.
To be assured that the multiplicity of the solution is one,let u=0 be the plane of μ3and ϱ2be represented by the planes x=0 and y=0.Then δμ3ϱ2is represented by the elements of δ in u=0 with double points on[u,x,y,z]=[0,0,0,1].
Now,let ν2be represented by two lines such that their intersections with u=0 are given by[0,1,1,1]and[0,1,-1,1].
The equations of the conics in u=0 passing through[0,1,1,1]and[0,1,-1,1]are given by
1+b+c+2d+2e+2f=0,
1+b+c-2d+2e-2f=0.
In the coordinate system (g,h,i,s,u,k2,d,e),as before,we have that g=h=i=0,and the above two equations become
us+(1+k2)2u+(d+e)2+2d+2e+1=0,
us+(1-k2)2u+(d-e)2-2d+2e+1=0.
The equations relevant to δ and ϱ2are

We substitute s=0 in the relevant equations of ϱ2,which yields (e-k2d)2=0 and=0.
Thus,the number of solutions of the above equations is four times the number of solutions of the following equations:

There is only one solution,
g=h=i=s=k2=e=0,u=-1,
with a multiplicity of one.
(4)δμ3νϱ3=0.This is because δμ3ϱ3is already an empty set,as we may take the three planes determined by ϱ3to intersect the planes of μ3to get three lines with no common point.
(5)δμ3ϱ4=0.ϱ4is already equal to 0.
(6)δμ2ν5=20.
μ2is represented by planes passing through a given line l.For five given lines in a general position,three of these and l determine two of the lines intersecting with the four lines.Each of these two lines and l determine a plane on which there is just one element in δ intersecting with the five given lines.Therefore,geometrically,there are just=20 elements in δμ2ν5.Now the serious problem that arises is why each element of these has a multiplicity of one.To prove this,we must use equations.
Let u+gx+hy+iz=0 be the planes,let x2+by2+cz2+2dxy+2exz+2fyz=0 be the conics on any above plane,and let μ2be represented by the planes satisfying g=i=0.
Let g1,g2,g3,g4,g5be given by the lines connecting the points
[u,x,y,z]=[0,1,1,1],[0,-1,-1,1],[0,0,-1,1],[0,0,1,1],[0,0,2,1]
and
[u,x,y,z]=[1,1,1,1],[1,-2,0,1],[1,-3,-4,1],[1,3,5,1],[1,1,2,1]
correspondingly.Then the equations of conics with g=i=0 intersecting with g1,···,g5are given by
G1=1+b+c+2d+2e+2f,
G2=(c-4e+4) h2+(2c+4d-6e-2f+4) h+1+b+c+2d-2e-2f,
G3=(9c+18e+9) h2+(-6c+6d-6e+6f) h+b+c-2f,
G4=(9+16c-24e) h2+(8c-6d-6e+8f) h+c+2f+b,
G5=4h2-4(e+2d) h+c+4b+4f.
Now H=cb-f2-e2b-d2c+2def is the equation for δ.By using‘wsolve’,we get 20 solutions of the equations
G1=G2=G3=G4=G5=H=0.
We only list the 20 solutions for h;that is

To show that these solutions are simple,we use‘wsolve’again to show that the above 6 equations,together with the Jacobian determinant of them equal to zero,have no solution.
(7)δμ2ν4ϱ=34.
Geometrically,we must show that the number of solutions is 17.We assume that Schubert’s argument is as follows:let l be the line so that μ2is represented by the planes passing through it,and let g1,g2,g3,g4be the lines representing ν4.
Then g1,g2,g3and l determine two lines,l1,l2,intersecting with the plane Γ determined by ϱ at two points,p1,p2.Connecting these with the point that is the intersection of the planes determined by liand l with g4,we get two elements of δ with double points on Γ.In this way,we get 8 elements of δμ2ν4ϱ.
We recall the equation 9),g2=gp+ge,in Section 2 of[1],which means the condition that a straight line passing through two given lines is equal to the condition that a straight line passes through a given point or that this straight line lies on a given plane.Thus the condition that a line passes through g1and g2is equivalent to the condition that the line passes through a given point p1,or that the line lies on a given plane e1.The condition that a line passes through g3and g4is equivalent to the condition that the line passes through a given point p2,or that the line lies on a given plane e2.There is only one plane passing through the line l and the point p1in a general position.This plane intersects with plane e2at a line d2,and d2intersects with the plane Γ at a point p3.There is only one line d1passing through p3and p1.That is to say,there is only one element in δ satisfying that one of its straight lines passes through point p1,and the other lies on the plane e2.Also,there is only one element in δ satisfying that one of its straight lines passes through point p2,and the other lies on the plane e1.The plane e1intersects with e2at line d3,which intersects with Γ at point p4.There is only one plane e3that passes through p4and l.The plane e3intersects with e1at a line d1and intersects with e2at a line d2.The two lines d1and d2constitute an element in δ.Thus,we find three elements in δ whereby one of the lines passes through g1and g2and the other passes through g3and g4.There are=3 methods to choose two lines from four,so we get 3×3=9 elements in δμ2ν4ϱ.
Thus,Schubert came to the conclusion that 2(8+9)=34.
Coming to the equations,let G1,G2,G3,G4be de fined as in case (6),and let Γ be the plane x=0.l is g=i=0.In the coordinate system (g,h,i,s,u,k2,d,e),as before,the equations relevant to δ and ϱ are

The equations G1=0,G2=0,G3=0,and G4=0 become

We substitute s=0 in the relevant equations of ϱ,which yields that (e-k2d)2=0.Thus the number of solutions of the above equations is two times the number of solutions of the following equations:
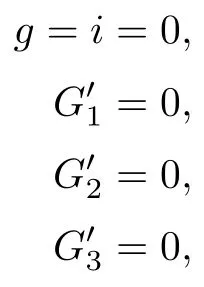
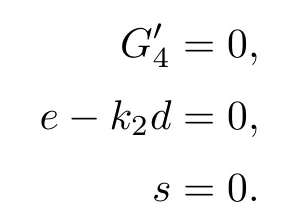
Using Rational Univariate Representation ([g,i,,e-k2d,s],v),we obtain 17 solutions,each of which has a multiplicity of one (i.e.,
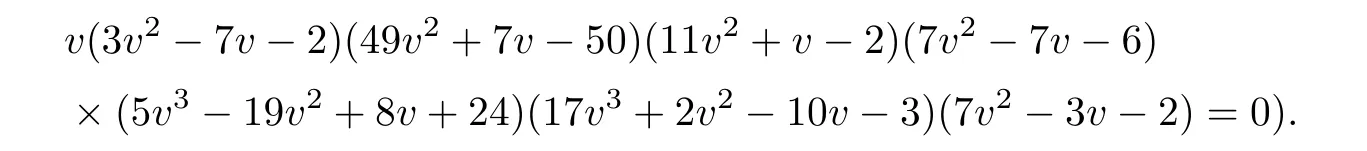
(8)δμ2ν3ϱ2=24.
Schubert calculated this number as an example,and we have already given it at the beginning of this section.
Now let μ2be given by g=i=0,let ϱ2be given by the two planes x=0 and u=x.Let the line g1,g2,g3be given by connecting the points
[u,x,y,z]=[1,1,1,1],[2,21,0,1],[4,-5,-2,1]
and
[u,x,y,z]=[2,-10,11,1],[-7,0,12,1],[16,12,3,1].
Then the equations of conics with g=i=0 intersecting with g1,g2,g3are given by

In the coordinate system (g,h,i,s,u,k2,d,e),as before,the equations relevant to δ and ϱ2are

The equations G6=0,G7=0,and G8=0 become=0,=0,and=0,with b,c,f replaced by u+d2,(s+) u+e2and k2u+de,respectively.
Substituting s=0 in the relevant equations of ϱ2yields (e-k2d)2=0 and (i-e-eg+k2(d-h+gd))2=0,so the number of solutions of the above equations is four times the number of solutions to the following equations:
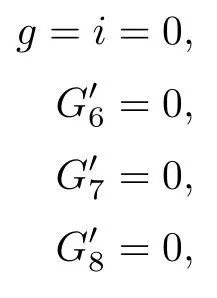
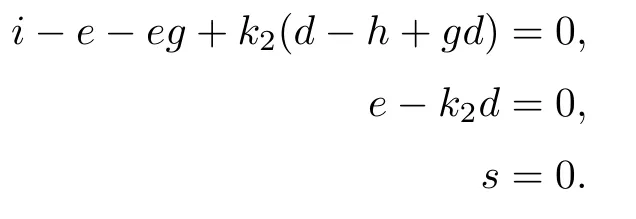
Using
RatinalUnivariantRepresentation ([g,i,,i-e-eg+k2(d-h+gd),e-k2d,s],v),
we have

From this,all the solutions must have a multiplicity of 1.Hence,δμ2ν3ϱ2=24.
(9)δμ2ν2ϱ3=8.
δϱ3is represented by the elements of δ with double points at the intersection of the three given planes relevant to ϱ3.δμ2ν2ϱ3is represented by those in the unique plane determined by the two points relevant to μ2and the double point.Then the double point,together with the two intersection points given by the lines relevant to ν2,determines the unique solution for δμ2ν2ϱ3.
Let the three planes relevant to ϱ3be x=0,y=0,u=x,and let μ2be represented by the planes through the points[u,x,y,z]=[1,0,1,1]and[1,1,1,1].Then
1+h+i=0 and 1+g+h+i=0
give g=0,i=-1-h.Furthermore,let ν2be represented by the lines x=0,y=1 and x=1,y=1.Then the equations for conics intersecting with them are

In the coordinate system (g,h,i,s,k2,u,d,e) given by b=u+d2,c=(s+) u+e2,and f=k2u+de,the above two become
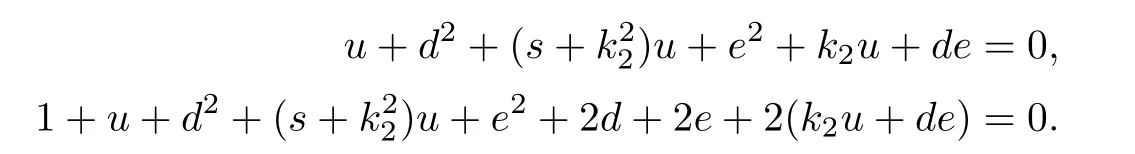
The condition δϱ3is 23times the condition
s=k2=e=i=0
with a multiplicity of one.Thus,the above becomes
u+d2=0,1+u+d2+2d=0.
These,together with g=0,i=-1-h,give the unique solution
g=0,h=-1,d=-1/2,u=-1/4,
with a multiplicity of 1.Thus,δμ2ν2ϱ3=8.
(10)δμ2νϱ4=0.
(11)δμ2ϱ5=0.
These are due to δϱ4=δϱ5=0.Since δϱ4is the condition for the double points of elements in δ on four planes,it is empty,and so is δϱ5.
(12)δμν6=70.
First,Schubert’s argument should be as follows:take 6 lines g1,···,g6in a general position.For any 4 of them,there are two lines that intersect with these four lines.Each of the two lines determines a plane by the condition μ.One of the lines determined by the 4 and the line obtained by connecting the 2 points which are the intersection points of the planes with the other 2 lines of the 6,determines a unique element in δ.Since=15,we obtain 30 elements in δμν6in this way.
Notice the equation 15),g3=2gs,in Section 2 of[1],which means that the condition that a line passes through three given lines is equivalent to two times the condition that a line is on a given plane and passes through a given point on it.Thus the number of elements in δμ satisfying that one of the lines passes through g1,g2,and g3and the other passes through g4,g5,and g6is four times the number of elements in δμ satisfying that one of the lines lies on a given plane e1and passes through a given point p1,and the other lies on a given plane e2and passes through a given point p2.The points p1,p2and the point determined by the condition μ determine only one plane where the element of δ should lie.Since=20,there are 10 ways to divide the 6 lines into 2 groups with each having 3 lines.Thus we get 40 elements in δμν6.
Therefore,to prove δμν6=70,we have to show that each of the 70 geometrical solutions has a multiplicity of one.
Let μ be represented by i-g=0.Let the special six lines g1,···,g6be given by connecting the points
[u,x,y,z]=[10,2,11,1],[6,3,-5,1],[2,-3,2,1],[-4,9,-2,1],[3,-9,-13,1],[13,2,5,1]
and
[u,x,y,z]=[2,3,5,1],[7,-3,-4,1],[7,4,2,1],[15,-3,2,1],[6,-2,4,1],[2,-3,2,1]
correspondingly.Then the conics in the plane u+gx+hy+i=0 satisfying x2+by2+cz2+2dxy+2exz+2fyz=0 intersect with the above six lines if and only if they satisfy the following six equations:
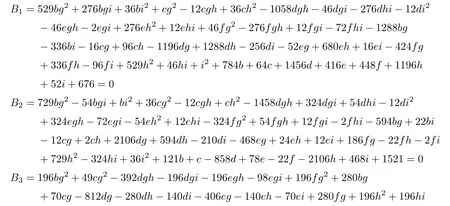


which shows that there are 70 solutions for δμν6.Therefore,all 70 solutions are simple.
(13)δμν5ϱ=100.
Schubert’s idea should be as follows:let g1,···,g5be the lines,let v be the point relevant to μ,and let the plane Γ be relevant to ϱ.Then δϱ implies the double point of an element of δ is on Γ.The two lines passing through allintersect with Γ at two points p1,p2.The two planes passing through the two lines,respectively,and the point v,intersect withat two points q1,q2.Then the two lines,together with the lines connecting piand qi,i=1,2,give two elements in δμν5ϱ.Thus,the situation regarding the multiplicities of the pairs are the same for the=5 choices of.Geometrically,we obtain ten solutions in this way.
As in the cases (7) and (12),we reasonably assume that Schubert should use the equations 9) and 15) in Section 2 of[1].The number of elements in δμρ satisfying that one of the lines passes through the lines g1,g2,and g3and the other passes through the lines g4and g5is two times the number of elements in δμρ satisfying that one of the lines lies on a given plane e1and passes through a given point p1and that the other passes through a given point p2or lies on a given plane e2.There is only one plane e3that passes through the point p1,the point p2,and the point determined by the condition μ.The plane e3intersects with e1at one line d1,which intersects with Γ at point p3as the double point.Thus,we can find an element in δμρ satisfying that one of the lines lies on a given plane e1and passes through a given point p1,and the other passes through a given point p2.The plane e1intersects with e2at a line d4,which intersects with Γ at point p4as the double point.Thus there is only one element in δμρ satisfying that one of the lines lies on a given plane e1and passes through a given point p1,and the other lies on a given plane e2.Thus the number of elements in δμρ satisfying that one of the lines passes through the lines g1,g2,and g3and the other passes through the lines g4and g5is 4.In this way,we obtain=40 solutions.
To see the multiplicities of the 50 solutions,we use the coordinates (g,h,i,s,u,k2,d,e) for an affine open set in the blow-up.Let g1,g2,g3,g4,g5be as in the case (12).Let ϱ be represented by the plane x=0.In the coordinates (g,h,i,s,u,k2,d,e),we substitute b=u+d2,c=(s+) u+e2and f=k2u+de into B1=0,···,B5=0 to obtain=0,···=0.The equations relevant to δ and ϱ are

We substitute s=0 in the relevant equations of ϱ,which yields e-k2d=0.Thus the number of solutions to the above equations is two times the number of solutions to the following equations:
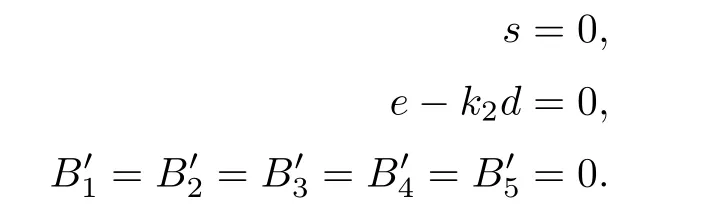
Again,let μ be represented by g-i=0.Then,by using
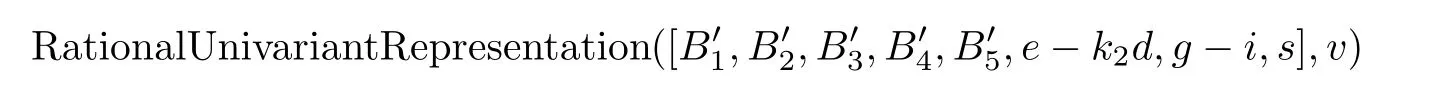
we obtain 50 solutions with a multiplicity of one:

The proof is complete.
(14)δμν4ϱ2=68.
Let gi,i=1,2,3,4 be the generic lines for ν4.The two planes relevant to ϱ2determine a line l so that δϱ2means the double points of δ in it are on l.Let η1,η2be the two lines which intersects with l and g1,g2,g3.hiand the point given by μ determine a plane which intersect with g4at a point pi.Then hi,together with the line which connects piand the intersection point of hiwith l,determines an element in δμν4ϱ2.In this way,we obtain eight solutions.
As in case (7),Schubert should use the equation 9) in Section 2 of[1].The condition that a line passes through g1and g2is equivalent to the condition that the line passes through a given point p1,or that the line lies on a given plane e1.The condition that a line passes through g3and g4is equivalent to the condition that the line passes through a given point p2,or that the line lies on a given plane e2.There is only one plane e3that passes the points p1,p2and the point determined by the condition μ.In addition to condition ρ2,there is only one element in δμρ2satisfying that one of the lines passes through the point p1and the other passes through the point p2.The line l intersects with e2at one point p3.There is only one line d1passing through p3and p1.Then,there is only one plane e4passing through d1and the point determined by μ.Thus,there is only one element in δμρ2satisfying that one of the lines passes through the point p1and that the other lies on the plane e2.Also,there is only one element in δμρ2satisfying that one of the lines passes through the point p2and that the other lies on the plane e1.To summarize,we get three elements in δμν4ϱ2.In this way,we obtain 3·=9 elements.
Now we come to the equations.Let ϱ2be relevant to the planes x=0 and u=x,and μ be given by g-i=0.
We also use the coordinates (g,h,i,s,u,k2,d,e) for an affine open set in the blow-up.Let g1,g2,g3,g4be as in the case (12).Then the relevant equations are
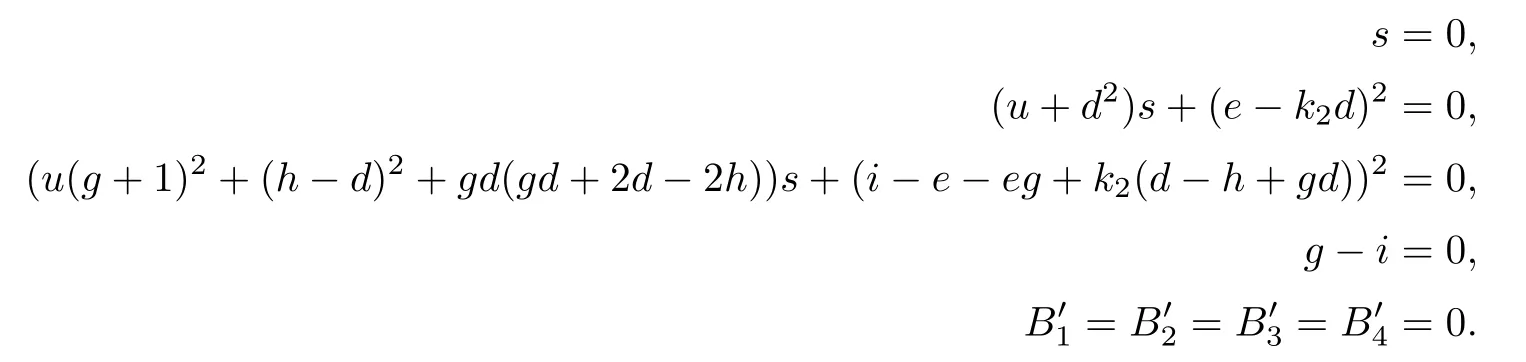
As before,the number of solutions to the above equations is four times the number of solutions to the following equations:

and
RationalUnivariateRepresentation ([,s,e-k2d,i-e-eg+k2(d-h+gd),g-i],v) gives


which shows that there are 17 simple solutions.Thus δμν4ϱ2=68.
(15)δμν3ϱ3=24.
δϱ3means the double points of the elements of δ are all on one point p.The point p,together with g1,g2,determines a unique line l passing through them.Line l,together with the condition μ determinines a plane intersecting with g3at a point q.Then l and the line connecting p and q give an element in δμν3ϱ3.In this way,we obtain 3 elements.
Let ϱ3be represented by the planes y=0,x=0 and u=x,and let ν3be represented by g1,g2,and g3in case (12).Also,μ is represented by g-i=0.
As with the method discussed before,we use the coordinates (g,h,i,s,u,k2,d,e).Then the relevant equations are

The number of solutions to the above equations is eight times the number of solutions to the following equations:
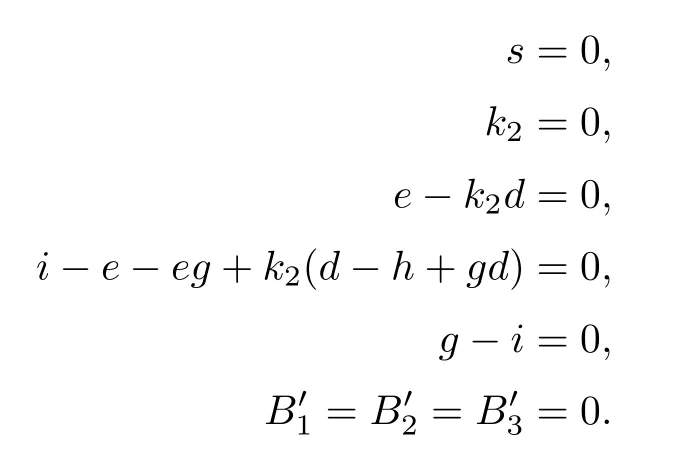
Finally,
RationalUnivariateRepresentation ([,s,k2,e-k2d,i-e-eg+k2(d-h+gd),g-i],v)
gives
(23744v-24555)(10060v-17889)(13684v-56535)=0,
and we are done.
(16)-(18)δμν2ϱ4=δμνϱ5=δμϱ6=0 are trivial.
(19)δν7=140.
Let g1,···,g7be the lines relevant to ν7.Any four of the seven determine two lines.For the left three lines,as in case (12),the condition that a line passes through them is equivalent to two times the condition that a line lies on a given plane e and passes a given point p.There are two elements in δ satisfying that one of its lines passes through the four chosen lines and let the other lies on a given plane e and passes through a given point p.Thus,we have 4 in δν7for any choice of four from the seven.Hence δν7has=140 elements geometrically.
Now,let g1,···,g6be the lines as in (12),and let g7be the line that passes[u,x,y,z]=[4,5,4,1]and[u,x,y,z]=[3,2,6,1].Then we get the equation B1,B2,···,B6as before,and



From this result,we see that there are 140 simple solutions,so each solution for generic g1,···,g7must be simple.We are done.
(20)δν6ϱ=140.
Schubert calculated this number as an example,and we have shown it at the beginning of this section.We need to check the multiplicity.
Let B1,B2,B3,B4,B5,and B6be as in the case (12).Then,letting
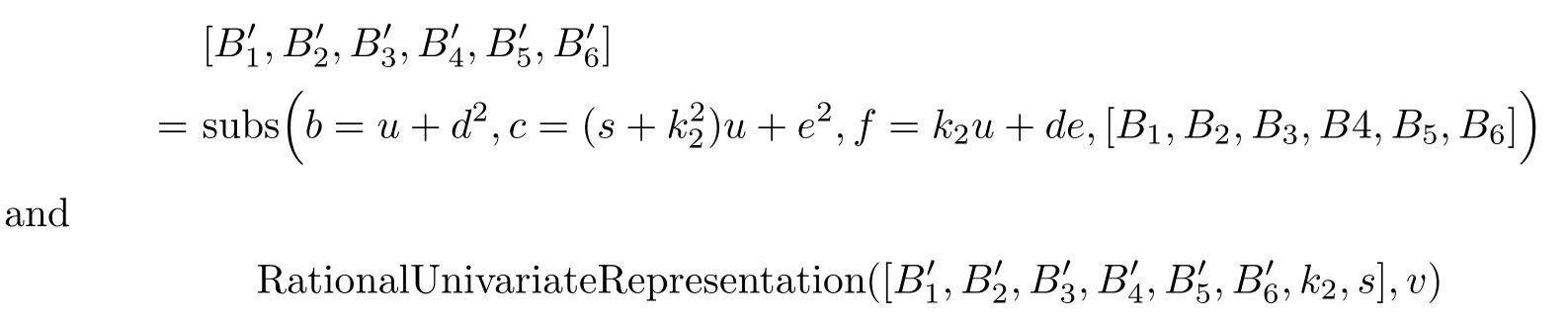
gives the following:


From this we see that there are 70 simple solutions,so all 70 solutions in the generic case must be simple.
(21)δν5ϱ2=80.
δϱ2means the double points of the elements of δ are on a line l.The lines g1,g2,g3and l determine two lines,l1,l2,intersecting with l at two points p1,p2.Each pjdetermines a linepassing through pjand g4,g5.Thus,ljandgive an element in δν5ϱ2.Thus δν5ϱ2has=20 elements.
To see that all elements have a multiplicity of one,let ϱ2be represented by the planes y=0,x=0,and let B1,B2,B3,B4,B5be as in case (12).We have


The above shows that the 20 solutions are all simple.
(22)δν4ϱ3=24.
δϱ3implies that all the elements of δ satisfying this condition have the same double point.The lines from this point to g1,g2and to g3,g4give an element in δν4ϱ3,so there are just three elements.
To see that all elements have a multiplicity of one,let ϱ3be represented by the planes y=0,x=0 and u=x,and letbe given as before.Now,

gives
(94564v-195255)(357008v-1093113)(37631v-107364)=0,
so the three elements are simple,and
δν4ϱ3=8·3=24.
(23)-(26)δν3ϱ4=δν2ϱ5=δνϱ6=δϱ7=0 are trivial.
(27)ημ3ν4=0.
Since ην4implies that there are only two possible double lines which cannot be in the unique plane given by μ3in general,so ημ3ν4is an empty set.
(28)ημ3ν3ϱ=0.
μ3determines a plane.The three lines relevant to ν3intersect this plane at three points in a general position.No double line can pass through these three points,so ημ3ν3=0.
(29)ημ3ν2ϱ2=4.
ημ3ν2implies that there is only one double line l in the plane determined by μ3and passing through the two intersection points of the plane and the two lines determined by ν2.The two planes determined by ϱ2intersect with l at two points,which,together with l,give the unique one in ημ3ν2ϱ2.
To see that this solution is simple,let ν2be represented by the lines
g1:u=0,y=x;g2:u=0,y=z.
Let μ3be represented by the plane u+gx+hy+iz=0 with g=h=i=1,and let ϱ2be represented by x=z and x=2z with relevant equations
L1=(f+d)2-b-bc-2be,
L2=(f+2d)2-4b-bc-4be.
After the substitutions
b=k1v+d2,c=v+e2,f=k2v+de,
the condition ην2is four times the variety
v=0,di-eg-eh+i=0,i+h-dg-eg=0.
These,together with g=h=i=1,give the variety
e=1,d=1
with a multiplicity of one.
The proper transformations of L1=0,L2=0 are
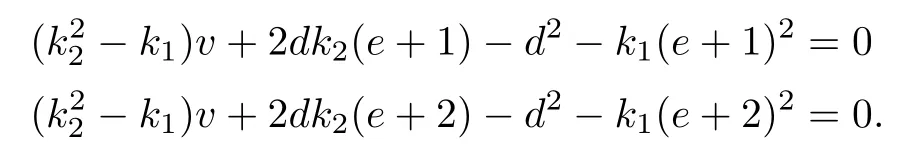
Thus v=0 and d=e=1 give solution

with a multiplicity of one.
(30)ημ3νϱ3=6.
ημ3ν implies that the double lines are those on a plane Γ given by μ3and pass through the intersection point p of the plane with the line determined by ν.Let p1,p2,p3be the points on Γ which are intersection points of Γ and two of the three planes determined by ϱ3.Then the double line connecting p and pjintersects with one of the three planes not passing through pjat a point qj.This double line,together with pjand qjon Γ,gives an element in ημ3νϱ3for j=1,2,3.Thus
ημ3νϱ3=2·3=6.
Now,let μ3be represented again by g=h=i=1,let ν be represented by the line u=0,y=0,and let ϱ3be represented by the plane x=0,x=z and u=x.
Then the same procedure as above yields three simple solutions:

(31)ημ3ϱ4=3.
On the plane Γ determined by μ3,there are just12C24=3 pairs of points,each pair of which is the intersection points of Γ and two groups of the four planes given by ϱ4with each group containing two planes.The double line connecting each pair of points with that pair of points gives an element in ημ3ϱ4,thus there are 3 such elements.
Take the special case such that μ3is represented by u=0,and ϱ4is represented by the planes
x=0,y=0,x=y+z,x=-y+2z.
Then the equations for the conics tangent to these are given by f2-bc=0,c-e2=0 and J1=0,J2=0,where
J1=bc+2be+2cd-d2+2de-2df-e2-2ef-f2+b+c-2f,
J2=bc+4be-2cd-4d2-4de-4df-e2+2ef-f2+4b+c+4f.
Substituting b=u+d2,c=k1u+e2,and f=k2u+de into these,then dividing them by u,we obtain the proper transformations of ϱ4:

Then
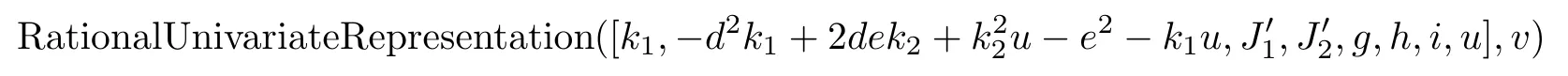
gives
(4v+1)(2v-1)(v+1)=0.
From this,we see clearly that there are just three simple solutions.
(32)ημ2ν5=0.
This is due to the fact that no line passes through five lines in a generic position.
(33)ημ2ν4ϱ=0.
This is because ημ2ν4is already empty.
(34)ημ2ν3ϱ2=16.
There are only two lines that pass through the three lines determined by ν3and the line connecting the two points determined by μ2.Thus we obtain two double lines,and their intersections with the two planes determined by ϱ2make them elements of η.
To see that the two solutions are simple,let ν3be represented by the lines g1,g2,and g3as in case (12),let μ2be represented by g=i=0,and let ϱ2be represented by the two planes y=0 and u=x.Thus,for the coordinates (g,h,i,u,k1,k2,d,e,),we get the following equations:
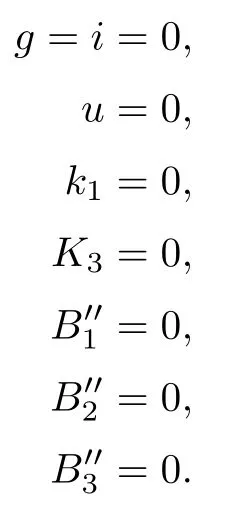
Here K3is given in the proof of Schubert’s second assertion,andcan be obtained by substituting b=u+d2,c=k1u+e2,and f=k2u+de into B1,B2,and B3,respectively.Then

so the number of solutions to the above equations is eight times the number of solutions to the following equations:


Then
RationalUnivariateRepresentation ([C1,C2,C3,g,i,u,k1,K3],v)
gives a polynomial of v,
1424700v2-8262209v+26168304=0.
From this we see clearly that ημ2ν3ϱ2=16.
(35)ημ2ν2ϱ3=24.
Let Γ1,Γ2,and Γ3be the three planes determined by ϱ3.There are three cases for choosing two of them.Let Γ1,Γ2be two of these.Then their intersection line,together with the two lines determined by ν2and the line relevant to μ2,determine two lines.Each one of the lines,together with its intersection point on the intersection of Γ1(i.e.,Γ2),and its intersection point on Γ3,gives an element of ημ2ν2ϱ3.Thus there are just six elements in ημ2ν2ϱ3.Counting their multiplicity as four,we obtain 24.
To check the above,let B1,B2be the polynomials determined by ν2as,in the case (12).Let the three planes relevant to ϱ3be x=0,y=0,u=x,and let μ2be represented by the planes through the points[u,x,y,z]=[1,0,1,1]and[1,1,1,1].Then,for the coordinates (g,h,i,u,k1,k2,d,e,),we get the following equations:

where K3is given in the proof of Schubert’s second assertion,andis just the same as in the case (34).Thus,the number of solutions to the above equations is four times the number of solutions to the equations
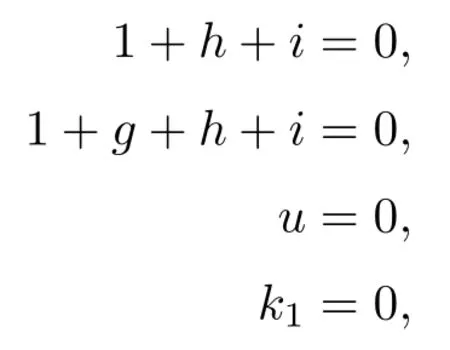

Finally,
RationalUnivariateRepresentation ([1+h+i,1+g+h+i,u,k1,K2,K3,C1,C2],v)
gives a polynomial of v,
(29328v2-313030v-154893)(4176v2+15188v-33699)(94v2-1075v-1551)=0.This shows that the answer 24=4×6 is correct.
(36)ημ2νϱ4=20.
An element in η is tangent to four planes determined by ϱ4if and only if,a) one of its special points is on three planes,i.e.,on their intersection point,and another special point is on the other plane;and b) one of its special points is on two of the planes,and another on the other two.
For b),the intersection line of the two of the four and that of the other two together with the line determined by ν and the line relevant to μ2determine two lines that intersect with all of them.This line,together with the two special points given by its intersection points with the two intersection lines of the four planes,gives an element of η.Thus,b) offers 2·=6 solutions.a) together with b) offers 10.Thus the answer is 2×10=20.
Let B1be as in case (35).Let the four planes relevant to ϱ4be x=0,y=0,u=x,and u=2x+y+z,and let μ2be represented by the planes through the points[u,x,y,z]=[1,0,1,1]and[1,1,1,1].
Then the procedure,as for case (35),gives that
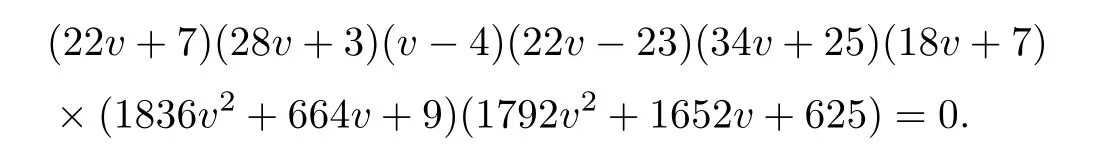
This shows that the answer is correct.
(37)ημ2ϱ5=10.
The only possibilities for an element being tangent to five planes are that it is tangent to three of them at their intersection point p and to the other two at their intersection line L.There is a unique plane in μ2passing through p.Let the intersection point of this plane and L be q.Then p and q,together with the line passing through these,give an element in η,and
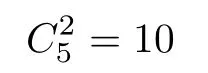
gives the answer.
To check the multiplicities,let the four of five planes determined by ϱ5be as in case (36);the fifth one is given by 6u-5x-4y-2z=0,and μ2is given by the point[u,x,y,z]=[1,0,1,1]
and[1,1,1,1].Then,the RationalUnivariateRepresentation gives ten simple solutions:

Hence ημ2ϱ5=10 is correct.
(38)ημν6=0.
(39)ημν5ρ=0.
These are due to the fact that there is no line passing through five lines in a general position.
(40)ημν4ρ2=32.
There are only two lines that pass through four lines in a general position.Any of these lines intersects each plane determined by ρ with one point which should be the special point.The line with two special points on it,whose plane is the only plane that contains it and the point determined by μ,is an element in η.Thus,by Schubert’s first observation about the condition ην4,the answer is 24×2=32.
To see that all the solutions are simple,let ν4be represented by the lines g1,g2,g3,and g4as in case (12).Let μ be represented by g-i=0 and let ρ2be represented by the two planes y=0 and u=x.For the coordinates (g,h,i,u,k1,k2,d,e),we get the following equations:

Here K3is given in the proof of Schubert’s second assertion,andcan be obtained by substituting b=u+d2,c=k1u+e2,f=k2u+de in B1,B2,B3,B4,respectively.

Thus the number of solutions to the above equations is sixteen times the number of solutions to the equations

Thus,
RationalUnivariateRepresentation ([C1,C2,C3,C4,g-i,u,k1,K3],v)
gives a polynomial of v,
1412932859v2+7504678041v+8510994946=0,
which shows that the answer 24×2=32 is correct.
(41)ημν3ρ3=48.
Schubert’s calculation should be as follows:according to equation 15) in Section 2 of[1],the condition that a line passes three lines in general position is equivalent to two times the condition that a line lies in a given plane e and passes a given point p.Denote the three planes determined by ρ3by Γ1,Γ2,and Γ3.Choose any two of them,such as Γ1and Γ2.The three planes,e,Γ1,and Γ2,intersect at one point p3.There is only one line d3that passes through p and p3.One of the special points is p3,and the other one is the intersection point of d3and Γ3.There is only one plane that contains d3and the point determined by μ.Thus,we get one element in η.As there are three methods to choose two planes out of three,according to the first observation by Schubert regarding the condition ην3,there should be
23×2×3=48
elements in ημν3ρ3.
Now let us come to the equations.Let ν3be represented by the lines g1,g2,and g3as in case (12).Let μ be represented by g-i=0 and let ρ3be represented by the three planes x=0,y=0,and u=x.For the coordinates (g,h,i,u,k1,k2,d,e),we get
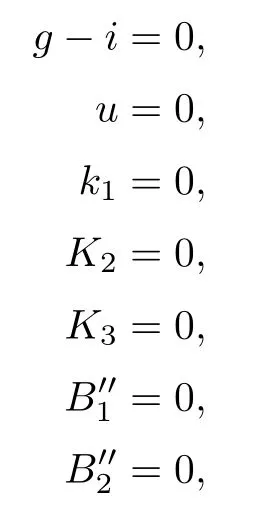
where K2,K3is given in the proof of Schubert’s second assertion,andcan be obtained by substituting b=u+d2,c=k1u+e2,f=k2u+de in B1,B2,B3,B4,respectively,as in case (40).
Therefore,the number of solutions to the above equations is eight times the number of solutions to the equations

Finally,
RationalUnivariateRepresentation ([C1,C2,C3,g-i,u,k1,K2,K3],v)
gives a polynomial of v,
(2184540v2-11632756v+4577631)(1583v2-7977v-4023)(1588535v2+23093808v-144828)=0,
which shows that the answer 23×6=48 is correct.
(42)ημν2ρ4=40.
Schubert calculated this number as an example,as we mentioned at the beginning of this section.
For multiplicity,we choose μ to be represented by the plane passing through the point[u,x,y,z]=[1,0,1,1],ν2be represented by g2,g3as in case (40),and let ρ4be represented by the four planes as in case (36).Then the command‘RationalUnivariateRepresentation’gives

which shows the validity of ημν2ρ4=40.
(43)ημνρ5=20.
First,we follow Schubert’s idea to get the geometric solutions.The five planes determined by ρ5can be divided into two groups to determine the two special points on the double line.The first group contains three planes and the second group contains the remaining two planes.The first special point should be the only intersection point of the three planes in the first group.The double line should be the only line that passes through the first special point,the line determined by ν,and the intersection line of the planes in the second group.The second special point must be the intersection point between the double line and the intersection line of the planes in the second group.There is only one plane that contains the double line and the point determined by μ.According to the first observation of Schubert about the condition ην,we get

geometric solutions.
Now,we need equations to calculate the multiplicities of these solutions.We choose μ to be represented by the plane through the point[u,x,y,z]=[1,0,1,1],let ν be represented by g1in the case (40),and let ρ5be represented by the five planes in the case (37).Then the command‘RationalUnivariateRepresentation’gives
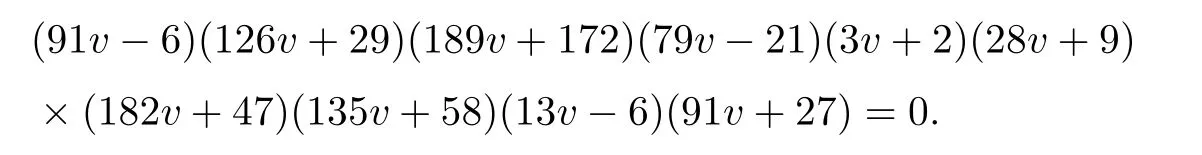
Hence,ημνρ5=20 is correct.
(44)ημρ6=10.
Schubert’s idea should be as follows:the six planes determined by ρ6can be divided into two groups to determine the two special points on the double line.Each group contains three planes.The two special points should be the intersection points of three planes in each group.The double line must be the line connecting these two special points.There is only one plane that contains the double line and the point determined by μ.Thus,we get=10 elements in ημρ6.
For multiplicity,we choose μ to be represented by the plane through the point[u,x,y,z]=[1,0,1,1],and let ρ6be represented by the five planes in (43) plus the plane u-7x-2y-4z=0.Then the command‘RationalUnivariateRepresentation’gives

which proves that ημρ6=10.
(45)ην7=0.
(46)ην6ϱ=0.
(47)ην5ϱ2=0.
These are due to the fact that there is no line passing through five lines in a general position.
(48)ην4ϱ3=0.
This is because there are only two lines passing through the four lines determined by ν4,and it is impossible for these two lines to intersect with the intersection line of any two planes in a general position.
(49)ην3ϱ4=0.
This is because there is no line passing through the three lines determined by ν3and the two lines given by ϱ4or the point given by ϱ3.
(50)ην2ϱ5=0.
This is due to the fact that there is no line passing through the two lines determined by ν2together with the line given by ϱ2and the point given by ϱ3.
(51)ηνϱ6=0.
If a line passes through the point given by three of the six planes determined by ϱ6and the point given by the remaining three of the six planes,then it is impossible to pass through the line of ν in a general position.
(52)ηϱ7=0.
This is because there is no line that is able to intersect with the seven planes in a general position at one or two points.
5 The Formulas about μ,ν,and ϱ
Now,by using formulas 1) and 2) from the introduction,we see how Schubert was able to calculate all of μmνnϱ8-m-n.We start by calculating the terms containing μ3,then those with μ2,μ and μ0.The checking only concerns if Schubert had mistakes in calculations or typos.



杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- MOMENTS AND LARGE DEVIATIONS FOR SUPERCRITICAL BRANCHING PROCESSES WITH IMMIGRATION IN RANDOM ENVIRONMENTS*
- FURTHER EXTENSIONS OF SOME TRUNCATED HECKE TYPE IDENTITIES*
- ASYMPTOTIC GROWTH BOUNDS FOR THE VLASOV-POISSON SYSTEM WITH RADIATION DAMPING*
- CONVERGENCE RESULTS FOR NON-OVERLAPSCHWARZ WAVEFORM RELAXATION ALGORITHMWITH CHANGING TRANSMISSION CONDITIONS*
- RIEMANN-HILBERT PROBLEMS AND SOLITONSOLUTIONS OF NONLOCAL REVERSE-TIME NLS HIERARCHIES*
- THEORETICAL AND NUMERICAL STUDY OF THE BLOW UP IN A NONLINEAR VISCOELASTIC PROBLEM WITH VARIABLE-EXPONENT AND ARBITRARY POSITIVE ENERGY*
