基于离散元法的铁路沿线非饱和边坡流动与冲击分析
2022-03-12余朝阳杨彦海孙大奇罗刚谢伟
余朝阳 杨彦海 孙大奇 罗刚 谢伟
1.川藏铁路有限公司,成都 610041;2.四川大学建筑与环境学院,成都 610011;3.中国国家铁路集团有限公司工程管理中心,北京 100038;4.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081;5.西南交通大学地球科学与环境工程学院,成都 610036;6.西南交大(上海)智能系统有限公司,成都 610031
云南普洱地区铁路修建过程中降雨触发的崩塌、泥石流灾害屡见不鲜。在边坡表面土体达到饱和之前,往往会在非饱和状态下发生小规模崩塌,而此类崩塌很可能发生在陡峭的铁路沿线,因此需要对这些边坡进行适当的维护。通常可在边坡表面使用复合材料[1]或者底部设置边坡防护措施,防止泥沙倒流[2-3]。已有研究认为可以将此类山体崩塌看作固体行为,进而探讨流动和冲击力产生机制[4]。非饱和土发生流动冲击现象时通常在低约束压力下伴随大变形和断裂现象,因此很难寻找满足这些条件的本构模型[5-6]。然而,采用运动方程追踪粒子单位行为的离散元法[7](Discrete Element Method,DEM)进行数值模拟可以有效解决此类问题。当前岩土工程中针对土体的各项参数分析以及不同破坏形态的离散元分析也在持续发展[8-10]。
本文以云南普洱一铁路修建现场典型降雨导致的山体崩塌为例,对铁路沿线非饱和土的边坡流动和冲击行为进行模型试验,并根据试验结果提出一个简便计算最大冲击力的公式。研究中再现非饱和土在黏聚力作用下产生的边坡流动特性和冲击行为,并评估黏附-再黏附粒子接触模型的适用性,在明确DEM法对非饱和土边坡冲击试验有效性的基础上进行崩塌土的数值模拟,并对边坡实物尺度崩塌土的流动行为和冲击力产生机理进行研究。
1 地质灾害概况
普洱市坐落于云南省西南部,云贵高原边缘,海拔高度不均,地形非常复杂,立体气候明显。区域大部分属于亚热带湿润气候,每年平均气温在10~15℃,年均降水量在1 500 mm左右,雨水充足。普洱市的基础建设中存在大量修建工程,诸如太达村隧道等。雨季诱发的铁路边坡失稳滑塌屡见不鲜,2016年10月及2018年8月,受强降雨的影响,铁路沿线均发生大量的山体崩塌,造成了铁路修建现场职工工棚冲毁,多人被困,人员伤亡惨重。
铁路沿线属低中山地貌,洞身分布下第三系渐新至始新统(E2⁃3)砾岩、砂岩夹泥岩(分布于进口至斜井段约4 000 m),白垩系下统曼岗组中段(K1m2)泥岩夹砂岩(分布于斜井至出口段约1 800 m)等。洞身发育普洱断裂西支和蛮帕山断层。雨季正常涌水量为1.2×104m3/d,最大涌水量为1.44×104m3/d。风险区域广泛分布于人工活动区及铁路沿线,主要为粉质黏土、黏性土、砂土等,力学性能较差,结构松散。该区域边坡崩塌堆积土堆积于边坡前缘,剪出口掩埋,一定程度上增加了边坡稳定性,减缓了边坡蠕滑变形速度。
2 考虑非饱和土黏附强度的简易黏附模型
2.1 粒子间黏附-再黏附接触模型
考虑到非饱和土的黏聚力作用,土体崩塌一般存在三种可能性:①土体在崩塌时破裂。②破裂的土体在与边坡支护结构冲击后堆积在一起。③边坡底部与边坡支护之间存在平滑带时,土体堆积在此区域。研究发现有必要建立边坡崩塌后可再次产生黏附效果的模型。因此,研究考虑了黏附-再黏附模型:当颗粒之间产生一定的拉伸力时会分离,但当颗粒再次接触时,又会产生黏聚力[11]。由于本文主要目的不是在微观层面上对非饱和土进行分析,而是从模型试验和数值模拟的角度分析非饱和土的行为,因此,主要针对土体颗粒之间相互接触时发生的宏观最大拉力作为黏附现象进行建模。破坏分析参数见表1。
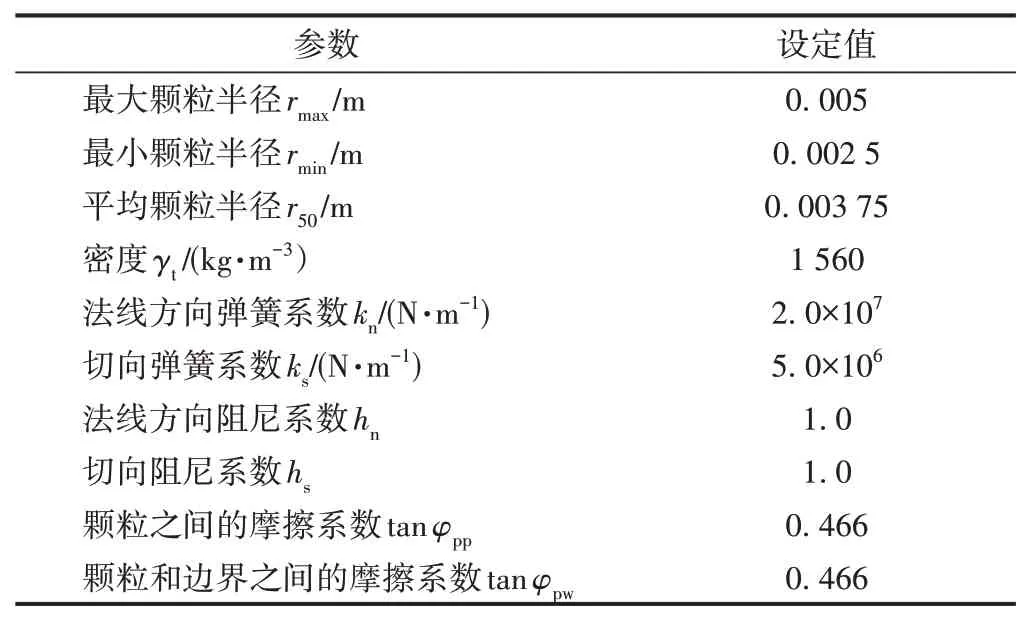
表1 破坏分析参数
DEM允许颗粒间黏附-再黏附的接触模型(简化的黏附模型)如图1所示,图中与黏聚力有关的接触模型用红色表示,其他基本接触模型用黑色表示。基本接触模型是一个在法线方向上弹簧和冲床并联的模型,并串联了一个分压器,当颗粒之间的距离超过一定值时,分压器就会阻止接触力发挥作用。在图1(a)所示的颗粒半径相对应的小范围内,使用了接触模型左侧所示的带有拉伸弹簧的无量纲DEM附着力影响半径rc。两个解析粒子在半径尺度的小范围内接近时,未发现二者发生接触。在实际的粒子尺度上,接触瞬间会产生一个极大的拉力,此时被认为进入接触状态,为了简化黏附现象,拉伸方向的弹簧系数被暂定为与压缩方向的弹簧系数相同。在黏附过程中,切向的接触力随着法向拉伸力的增加而增加。
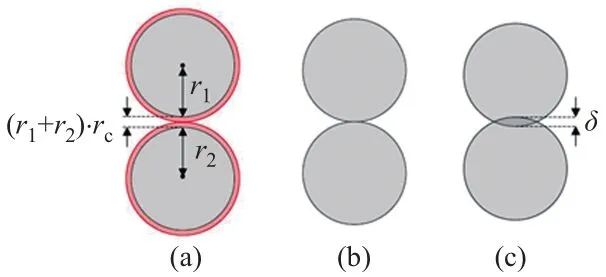
图1 颗粒间的黏附-再黏附接触模型颗粒间接触状态
2.2 基于简易黏附模型的DEM崩塌分析
为研究附着力影响半径rc对临界高度的影响,设置了1 m(宽)×1 m(高)的地基模型,从左右元件初始状态开始,通过将左侧的边界面下降0.1 m并释放应力来进行崩塌分析。崩塌分析时的参数参见表1。粒度分布是最大最小粒径比为2的均匀分布,在本文中,不仅通过改变黏聚力影响半径来进行模拟,还通过改变颗粒半径进行模拟分析。垂直边坡崩塌模拟结果见图2。可知,附着影响半径rc越大,临界高度就越大。此外,从活动塌陷面的角度估计内摩擦角约为25°,该值等于粒子之间摩擦系数。
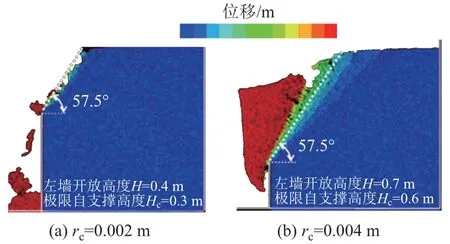
图2 垂直边坡崩塌的结果
临界高度可以通过极限分析法[11-12]或者极限平衡法[13]计算出的土体黏聚力c得到。垂直边坡崩塌分析结果,见图3。可知:附着力影响半径rc和临界高度几乎呈线性关系,并且通过将粒径减小到一定水平以下,临界高度会收敛。由此可说明,DEM颗粒水平的附着力影响半径(微黏聚力)与土体水平的宏观黏聚力之间存在线性关系。

图3 附着力影响半径和黏聚力的关系
在引入简易黏附模型的情况下,与不考虑黏附模型的普通DEM分析结果相比,塌陷后的沉积角更陡,沉积的粒子群中存在许多大间隙,研究再现了非饱和土的沉积行为。
2.3 不同坡角的边坡崩塌分析
对坡度60°、坡高0.1 m的边坡进行崩塌分析。最大颗粒半径为5 mm,附着力影响半径为0.002,边坡的崩塌分析结果见图4。可知:边坡高度小于等于0.5 m的边坡没有崩塌,边坡高度0.6 m时边坡变形显著,边坡高度0.7 m时边坡出现崩塌。若以有无滑移作为崩塌的指标,可以认为边坡的临界高度为0.5 m。

图4 不同边坡高度时60°边坡的崩塌解析结果
不同剪胀角ψ下,边坡角度和边坡稳定系数的关系见图5。可知:在剪胀角为0°的情况下,当边坡坡度从90°下降到60°时,稳定系数增加了约1.4倍。由于稳定系数与坡度高度成正比,在黏聚力和单位体积重量保持不变的条件下,稳定系数增加1.4倍意味着临界坡度高度增加1.4倍。
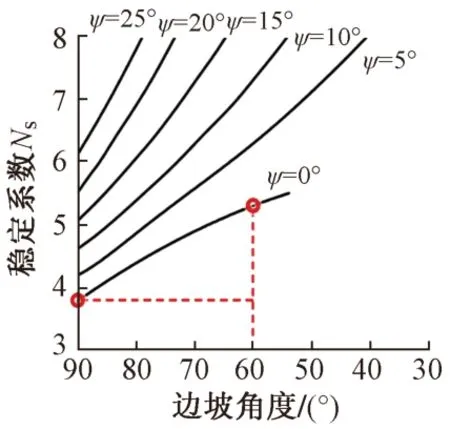
图5 边坡角度和边坡稳定系数的关系
本文的结果显示,坡度60°边坡在高度0.4 m时没有崩塌,而是在高度0.6 m时崩塌,这也证实了采用简化黏附模型的DEM可以大致再现边坡土体的黏聚力。
3 山体崩塌模型和非饱和试验分析
根据对现场的勘察显示,区域内平均崩塌深度为1.5 m,坡度多为25°~45°,尤其集中在30°~45°内更易触发。
3.1 模拟试验的概要
勘察发现,崩塌堆积体堆积于边坡前缘,对破坏起到了抑制作用,一定程度上增加了边坡稳定性,减缓了滑坡蠕滑变形速度。本文进行了非饱和土边坡的冲击试验,其中铝板安装在滑动面的底部。模型采用黏土,统一初始条件,含水率为10%,密度为1 560 kg/m3。试验中,测量了崩塌土初始厚度、初始长度和流动长度变化时的壁面冲击力。使用测力传感器以100 Hz的频率对壁面冲击力进行采样。
3.2 分析参数的设置
参数参见表1,无量纲粒子附着力影响半径为0.003。
3.2.1 弹簧系数
如果整个颗粒体的泊松比为1/3,弹性波P波与弹性波S波的速度比为2。对多质量点弹簧耦合系统中一维波传播速度的研究结果显示,法线和切线方向的弹簧系数与弹性P波、S波的平方成正比。根据这些结果,确定切线方向的弹簧系数是法线方向的弹簧系数的1/4。
弹簧系数设定为2×107N/m(法线方向的弹簧系数),再现了在低封闭压力下沙子的应力传播速度约为100 m/s。应力传播速度被定义为从自重下落冲击试验中自重接触砂子缓冲材料的时间(安装在自重上的冲击加速度计的上升时间)到在缓冲材料底部测得的传递冲击力达到1 kN以上的时间,也就是应力波传播时间以及缓冲材料的初始层厚度除以该时间。
3.2.2 摩擦系数
采用tanφ=0.466(φ为内摩擦角,φ=25°),颗粒与坡面之间的摩擦系数参照摩擦试验得到。在0.5 m(长)×0.2 m(高)的框架中构建了一个模型土体,当土体以大约0.01 m/s的速度在模型的边坡上滑行时,根据称重传感器的数值测量动摩擦系数。在摩擦试验中,土与坡面的摩擦系数为0.63,在DEM分析中取值一致。作用在底部元件上的切向接触力的时间波形与DEM分析结果一致。
3.2.3 附着力影响半径
试验时没有测量模型土的黏聚力,在崩塌土的初始长度为1.0 m、滑动长度为3.0 m的条件下,进行了不同初始厚度的边坡试验,即使崩塌土的初始厚度大于0.4 m也会出现崩塌,且与支护撞击时的土层厚度大致相同。据这个试验和图4的结果,本文采用了对应于临界高0.4 m的模型附着力影响半径0.003 m。
3.2.4 颗粒大小
最大颗粒直径与最小颗粒直径之比设为2.0,并采用了均匀的颗粒尺寸分布。颗粒尺寸越小,缓冲材料冲击时作用在重物上的最大冲击力越小[14]。由此可知当粒径小于一定值时,最大冲击力收敛到一个恒定值。边坡初始厚度0.2 m,边坡初始长度0.75 m,流动长度2.0 m,不同附着力影响半径时颗粒大小和冲击力关系见图6。
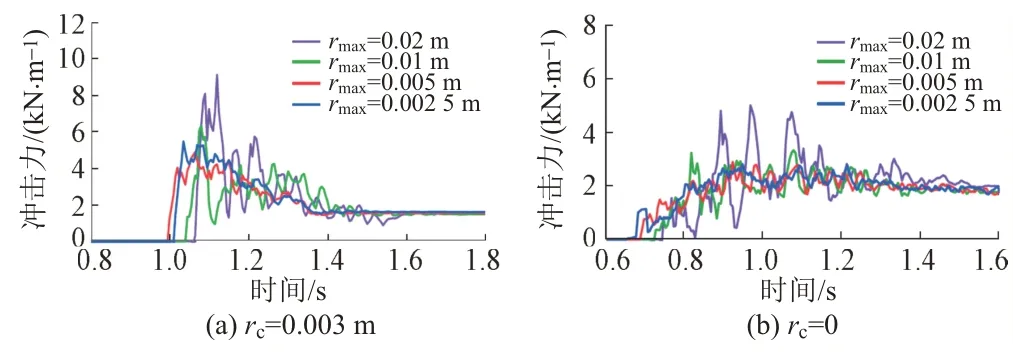
图6 不同附着力影响半径时颗粒大小和冲击力关系
由图6(a)可知:当最大粒子半径为0.005 m或更小时,最大冲击力趋于收敛,最大粒子半径为0.005 m的冲击力波形特征与0.002 5 m的冲击力波形特征几乎相同。由图6(b)可知:附着力影响半径rc=0的冲击力波形特征与rc=0.003 m的趋势基本相同。
颗粒大小与冲击壁面崩塌土形状的关系见图7,图中t为数值模拟解析时间。可知,当最大粒子半径小于0.005 m时,冲击时塌陷土趋于收敛。这一结果也与流体不影响沉积物流动试验的分析一致。基于上述分析,本文采用的最大粒子半径为0.005 m。
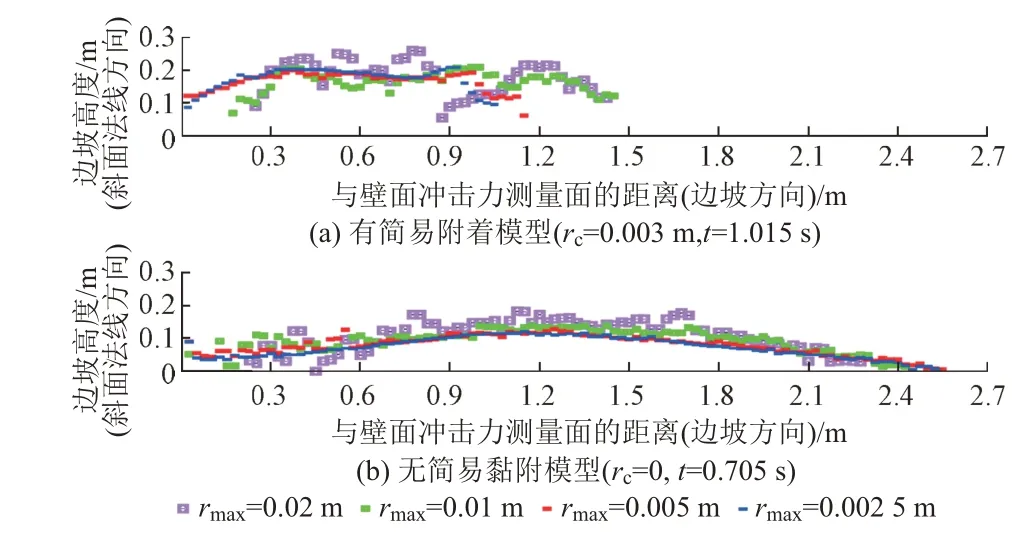
图7 颗粒大小与冲击壁面的崩塌土的形状的关系(解析结果)
3.3 模型试验和再现分析结果的比较
对模型试验结果和不同外力条件下再现分析结果进行比较,分析参数见表1。在试验中,负载是在100 Hz下测量的,因此进行了宽度为0.01 s的移动平均处理,使分析结果与其对应。
3.3.1 崩塌土的流动距离(冲击速度)
崩塌土冲击速度和最大冲击力的关系见图8。可知:最大的冲击力与冲击前的土体向支护的滑动速度有关。最大冲击力随着被撞土体的冲击速度增加呈增加趋势。
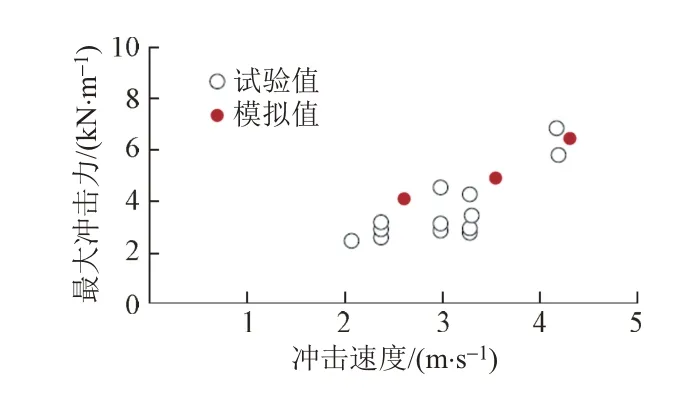
图8 崩塌土冲击速度和最大冲击力的关系
3.3.2 有无简易黏附模型对崩塌土的流动和冲击影响
在崩塌土初始厚度0.2 m,初始长度1.0 m,边坡长度3.0 m的条件下,在有简易黏附模型(rc=0.003 m,非饱和模型)和没有(rc=0,干燥模型)的情况下进行了冲击分析。冲击波形见图9。可知:与非饱和模型相比,干燥模型的冲击力较小,与试验结果大致一致,干燥模型的最大冲击力比非饱和模型小30%左右。
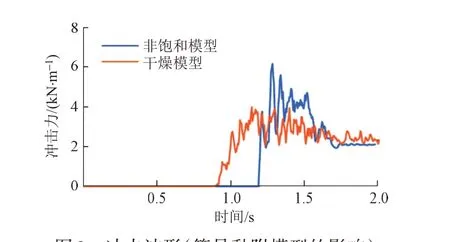
图9 冲击波形(简易黏附模型的影响)
冲击时非饱和模型保持了初始层的厚度,而干燥模型则很薄,并向破坏方向延伸。非饱和模型抑制了下坡速度,但由于在支护撞击时土层较厚,干燥模型的最大撞击力可能比非饱和模型的大。如果黏聚力相对于崩塌土的初始层厚度小,则干燥模型和非饱和模型冲击之前的崩塌土层厚度的差相对较小。由于干燥模型的坡面流动速度更大,所以认为非饱和模型的冲击力不一定比干燥模型大。
4 实物尺寸崩塌土的数值模拟分析
本文进行了基于崩塌案例的全尺寸土体的数值模拟试验,试验所得冲击力波形见图10。可知,两种情况下都产生了大于沉积物压力的冲击载荷,最大冲击力随着流动长度的增加而增加。

图10 冲击力波形(实物尺度的数值模拟)
依据试验提出了以下计算公式
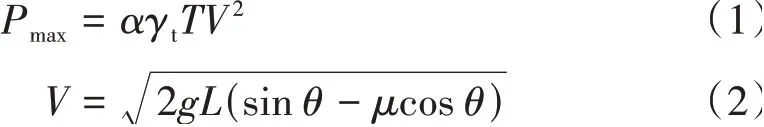
式中:Pmax为最大冲击力;α为系数;T为崩塌土的初期厚度;V为崩塌土的冲击速度;g为重力加速度;L为崩塌土的流动距离;θ为斜面的倾斜角度;μ为滑动摩擦系数。
L=10、15 m时崩塌土的速度分布见图11。可知,流动距离越长,碎土在坡面方向的分布越长,层厚越小。
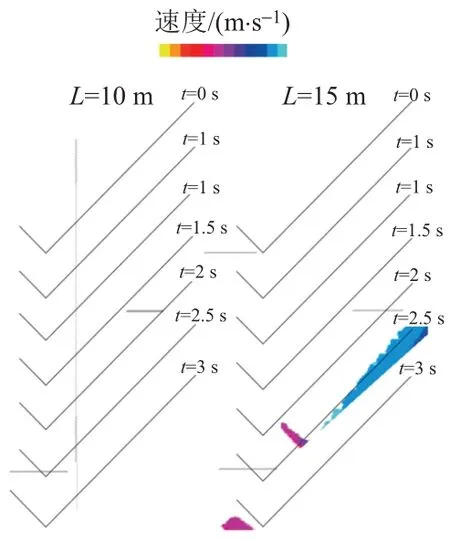
图11 崩塌土的速度分布(实物尺度的数值模拟)
在L=15.0 m时,最大冲击力发生时崩塌土的速度和接触力分布见图12。可知,超过3 kN的强接触力分布在距离墙面约1.5 m的地方,而相应点的速度分布是一个速度梯度为5~10 m/s的区域。这表明最大的冲击力是由距墙体1.5 m以上区域的速度梯度产生的接触力引起的,认为冲击力是由下面的塌陷土与前面沉积的1.5 m塌陷土冲击力传递而来。因此,在总结墙体最大冲击力原因时,最好能考虑到先前沉积的土体的缓冲行为。
图12 最大冲击力发生时崩塌土的速度与接触力分布
5 结论
1)为分析云南普洱某铁路沿线非饱和土边坡在持续降雨下黏聚力产生的影响,基于引入颗粒间的黏附-再黏附模型,可以通过DEM近似地再现黏聚力作用下的非饱和土边坡的坍陷行为。
2)通过将非饱和土的黏聚力以及土体与坡面的摩擦系数与各项分析参数相结合,可以在坡面流动和冲击试验中获得最大冲击力,并提出一个简易最大冲击力计算公式。
3)当支护上产生最大冲击力时,之前堆积在支护上的滑体可起到缓冲作用,抵御后续具有较大动能土体的冲击,而现场勘察发现边坡前缘的堆积土一定程度上增加了边坡稳定性,减缓了边坡蠕滑变形速度。
