一种遗传-贪婪融合算法求解多目标绿色柔性车间调度问题

高 滔，叶春明

（上海理工大学 管理学院，上海 200093）

0 引言

随着生产力的发展，能源消耗速度的不断升高导致的资源枯竭和环境问题日益严重，绿色制造已经成为了学术和企业界热议的话题[1]。绿色调度作为绿色制造的关键一环，作业车间调度中也愈加重视这一指标。

多目标柔性作业车间调度问题的求解难度较大，是NP-hard。当前求解该问题一种比较普遍和高效的方法是启发式算法，如遗传、蚁群、模拟退火算法等。钟祾充等[2]设计一种混合布谷鸟算法求解绿色流水车间调度问题。姚明明等[3]求解混合流水车间调度问题时以最大完工时间和总拖期为目标，改进了灰狼算法。孟冠军等[4]采用不同阶段不同搜索机制，并与禁忌搜索结合改进人工蜂群算法求解多目标柔性车间调度问题。王春等[5]求解多目标柔性车间调度问题时用区间数表示工序加工时间，并设计了一种进化算法解决。Dai等[6]在求解含有运输约束的多目标柔性车间调度问题时改进了遗传算法。Amiri等[7]用组合优化策略对多目标柔性车间调度问题进行求解。何东东[8]改进遗传退火算法用于求解柔性车间调度问题。弈飞等[9]求解低碳车间调度问题时加入自适应惯性权重和非线性收敛因子改进了鲸鱼算法。朱光宇等[10]设计了一种基于直觉模糊相似度的遗传算法求解多目标柔性车间调度问题。在王建华等[11]设计了一种基于Pareto最优解的自适应多目标Jaya算法求解带绿色指标的多目标柔性车间调度问题。解潇晗等[12]采用多层编码策略优化遗传算法并解决了面向能耗的多目标柔性车间调度问题。

多目标柔性作业车间调度问题多以算法改进和算法融合的方式求解，本文设计了一种基于遗传贪婪思想的混合算法（Genetic Greedy Fusion Algorithm，GGFA）求解。遗传部分：初始种群的工序编码随机生成、机器编码采用挑选最短加工机器与随机的方式生成[13]，适应度值等于优化指标统一量纲后求和，选择方式采用轮盘赌，交叉方式是单点与顺序交叉结合。贪婪部分：个体寻优时采用前后贪婪算子，设置贪婪上下限，实时更新非劣解表。最后通过算例求解验证效果。

1 多目标柔性车间绿色调度问题

1.1 问题描述

多目标柔性绿色车间调度模型描述如下：m个工件在n台机器上加工，工件i包含qi(i=1，2，…，m)道工序，qi不全相同，有工序可以在多台机器上加工且加工时间不等，可选机器集Mij∈{1，2，…，n}。优化目标是最大完工时间CM、机器总负荷TM和总能耗ET。

建立模型前对问题做出的一些假设：

1）同一台机器同一时刻只能加工一道工序；

2）任意工序只能被一个机器加工一次；

3）任意工序开始加工不能中断；

4）各个工件之间不存在的优先级的差别；

5）同一工件的工序之间存在先后约束；

6）所有工件在零时刻都可以被加工。

为方便讨论与读者对本文理解，对本文出现的符号作如表1定义。

表1 符号定义

1.2 模型建立

根据问题模型和假设条件，本文的调度模型以经济和绿色为目标，选择最大完工时间、机器总负荷和总能耗为目标函数；具体的数学模型如下：

其中式(1)、式(2)、式(3)表示最小化最大完工时间、总负荷和总能耗。式(4)表示工序开始加工就不能停止。式(5)表示任意工序只能在一台机器上加工一次。式(6)表示工序的先后约束。式(7)表示安排在相同机器上的工序，同一时刻只能加工一道。式(8)Xijz=1表示工序oij在机器z上加工，否则为0。式(9)Yijhk=1表示工序ohk在oij前加工，否则为0。

2 遗传贪婪融合算法

2.1 编码及解码

编码：采用基于机器和工序的2级实数编码方式。以每个工件含有两道工序的3×2完全柔性车间调度问题为例：如图1所示，该编码表示工件1和3的第一道工序分别在机器2和3上加工，其余工序的加工机器以此类推，这种编码方式能满足工序和机器约束。

图1 编码示例

解码：根据工序和机器编码转换出工序的加工时间，根据工序、机器和加工时计算每个机器的负载和终止时间。最大完工时间是最晚机器的终止时间。总负荷和总能耗分别是各机器的负荷和能耗之和，能耗根据空载和负载时间和具体的功率计算。

2.2 种群初始化

假设问题有m个工件，染色体长度为∑mi=1qi 。

工序编码：依次产生qi个i(i=1，2，…m)，随机打乱即可；

机器编码：假设sig∈[0，1]，在0，1之间生成随机数数rand，如果rand小于sig，所有工序随机挑选机器，否则所有工序挑选加工时间最短的机器。

2.3 适应度计算

对于每个染色体对应的最大完工时间、总负荷、总能耗。最大最小值法统一量纲。如式(10)所示，x，y分别对应各指标归一化前后的值，v为种群数量。适应度值取三个指标对应y(k)之和，且x(k)越小，y(k)越大，适应度值越大，个体就越优秀。

2.4 选择与交叉

选择：轮盘赌方法生成个体可重复的相同规模的种群。

交叉：顺序与单点交叉方式结合。选择得到的种群沟通依次两两一组交叉，具体方式如下：在1到之间随机生成一个整数作为交叉位置c，对于两个父代染色体C1、C2，分别在C3、C4存入C1、C2位置c前的染色体。C2去除C3的工序基因后与C3合并形成子代1。C1去除C4的工序基因后与C4合并形成子代2，机器编码作相应交换。

图2 MK01的一个可行调度方案

工序编码变异引起的机器编码变异较复杂，遗传部分主要考虑工序优化，所以不考虑变异。合并选择和交叉得到的种群，根据适应度值保留一半(v)个体进入贪婪操作。

2.5 非劣解表

大多多目标问题的求解是求出非劣解集，本文对完工时间、负荷和能耗寻Pareto占优进而找到非劣解集。非劣解表包含解的工序编码、机器编码及三个优化指标，初始为空，假设遗传优化后种群的第一个个体非劣，加入非劣解表，依次遍历种群个体，按照指标的支配关系不断添加或删除表里的解。

2.6 贪婪算子

以MK01为例，按照上述编码生成方法初始化一个可行调度方案如上，完工时间是86。最晚完工的机器和工件分别是M2和工件2。算例数据知工序O25的可选机器集是[6，2，1]，对应加工时间[5，6，1]。假设把工序O25安排到M1上加工，对应图中M2最后一个矩形移动到M1的工件6后面。最晚完工机器变成M4，最晚完工时间变短了，机器总负荷降低了5(O25加工时间由6变1)。空载时间不变，如果M2，M1负载功率差别不大，能耗也会降低。

由上面例子得到启发，考虑贪婪策略优化机器编码，完工时间的贪婪策略是把最晚完工机器的工序往其他机器安排。机器负荷的贪婪策略是把工序往加工时间短的机器安排。能耗的贪婪策略把工序加工时间少和功率低的机器安排。为减少算法复杂度和重复迭代，本文设计了前后贪婪算子，以后贪婪算子为例，算子步骤如下：

Step1：对染色体进行解码，输出最大完工时间、负荷、能耗、最晚完工机器、最早完工机器；

Step2：以最晚和最早完工机器在机器编码的位置为起点和终点，对机器编码反向遍历，记录基因等于最晚完工机器数的位置，读出工序并找到工序的可选机器集，如果可选机器个数为1，转Step5，否则转Step3；

Step3：工序挑选其他不同机器，机器编码对应位置的基因改变即可，工序编码不变，新的染色体个数为可选机器数减1。新的染色体按Step1方法解码；

Step4：旧染色体与第一个新染色体的三项优化指标作对比，如果部分新指标优于旧指标，更新染色体和非劣解表，否则不更新，转向与下一个新染色体比较。如果染色体发生更新，转Step2，否则结束贪婪；

Step5：是否搜索到终点，是结束贪婪，否则继续Step2；

前贪婪算子：正向遍历染色体，遍历的起点和终点是最早和最晚开始加工工件的机器的位置，其余类似。以2.1的编码例子为例，一个可行调度的工序和机器编码如下，假设机器2是最晚完工机器，其前后贪婪选择如图3所示。

图3 贪婪选择示例

2.7 算法流程

Step1：设置迭代次数，设置非劣解表，初始为空；

Step2：按2.2方法初始化种群，按2.3方法计算适应度；

Step3：按照2.4方法对种群进行选择交叉，找到优化种群的非劣解集及各项指标；

Step4：优化种群的每个个体按照2.6方法进行贪婪操作并更新非劣解表；

Step5：判断是否达到迭代次数和非劣解表是否更新，到达迭代次数或非劣解表未更新，结束算法，否则转Step2；

图4 算法流程

3 算法验证

MK01～MK07是工件、工序、机器数不全相同的柔性车间调度问题算例[14]，本文算法测试基于这7个例子。文献[15]的两个优化目标完工时间和能耗计算方式与本文相同。为实现算法对比，采用该文献设置的负载和空载功率，前后两个矩阵分别表示负载和空载功率，矩阵中功率的位次表示机器，如第一台机器的负载和空载功率分别是2和0.6。具体数据如下：

[2，1.8，1.6，2.4，2.4，4.1，3.5，4.1，2.8，2.7]，

[0.6，0.6，0.3，0.4，0.4，0.6，0.8，0.9，0.3，0.4]

设置迭代次数为20，种群规模为80，sig为0.8，交叉概率为0.8，对MK01例子进行最大完工时间，能耗、机器总负荷寻优，为清楚看出非劣解集的变化，该例子未加入非劣解集不更新结束算法的条件。其非劣解如表2所示，非劣解集中三个指标的最大、最小、平均值变化如图5所示。

表2 MK01算例结果

图5 非劣解中各指标的变化

图5中迭代次数为0是首次遗传操作后的非劣解集的各项指标，可以看出，第一次贪婪三个指标都有较大程度减低。第二次迭代后最大和平均时间完工上升，而能耗和负荷的相应指标下降，说明指标间存在矛盾关系，也说明该问题的指标无法优化到单目标下的结果。最小完工时间、最小能耗、最小负荷不增说明含有最小目标的解被保存下来。每个可行调度方案的工序以0.2概率选择了最短加工时间机器，即最小负荷，该例子是153，所以最小负荷一直不变。各指标在14次左右趋于平缓说明该算法收敛较快。

为近一步测试算法性能，算法的各参数与MK01相同，依照2.6的算法流程分别对MK01～MK07做三个目标和两个目标的寻优，结果如表3所示，前两列是对比文献的结果。并绘制MK03的最小完工时间下调度方案的甘特图如图6所示，时间是222。

表3 MK01～07算例结果对比

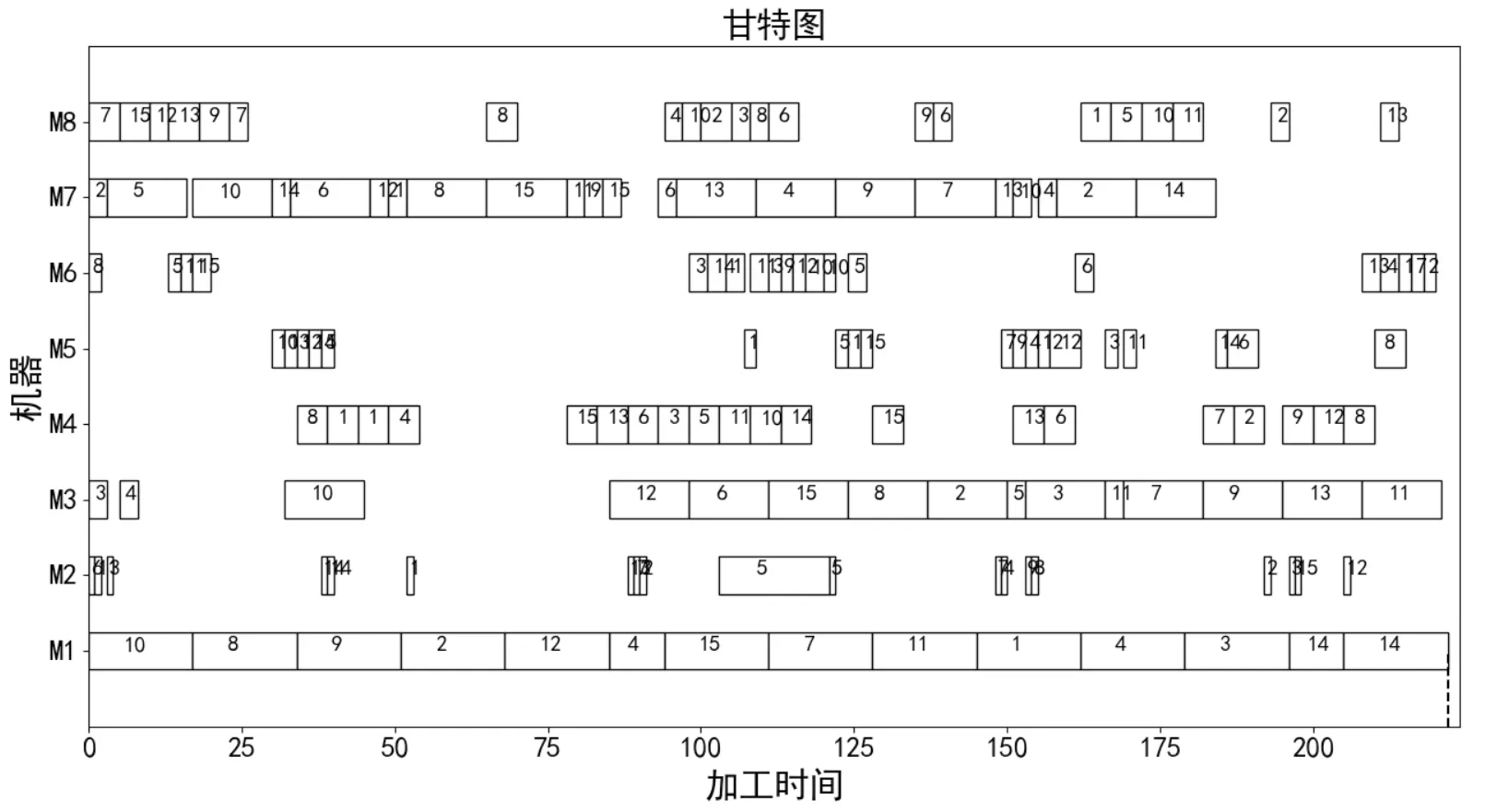
图6 MK03最小完工时间下的调度方案

表3第一行括号里的2，3表示目标数，其他行括号里的第一个数是非劣解的个数，第二个是完工时间的最大值，第三个是能耗最大值，第四个是负荷时间最大值。相较于前面2个算法，本文算法2个目标下在解的质量优于前者，在3个目标下的表现也较好。

4 结语

本文针对绿色车间调度问题建立以最小化最大完工时间、能耗和机器总负荷的为目标的调度模型。考虑遗传算法和贪婪算法结合对问题进行求解，在python平台进行仿真实验，得出问题的帕累托解，为决策者提供参考。并在最小化最大完工时间、能耗两个目标下与其他文献结果进行比较，验证了算法的可行性和有效性。