基于改进RRT算法的7-DOF机械臂运动规划

陈肇星，徐向荣，查文斌，杨 阳

（安徽工业大学 机械工程学院，马鞍山 243000）

0 引言

机器人是现代制造业的关键装备，也是智能时代将数据融入生活的重要设备。七自由度机械臂由于具备独特的冗余运动特性和近似于人手臂的灵活性，被广泛应用。为了开发冗余机器人的工作潜力，工程师们对冗余机械臂的运动学和动力学特性进行研究，机械臂的路径规划是一个重点方向。而路径规划有两种研究方向，在关节空间规划和在任务空间进行规划。本文中就采用在机械臂的关节空间规划，避免在工作空间进行路径规划时，需要大量的冗余臂逆运动求解而影响路径规划速度。

串联机械臂主流的路径规划方法有三种：基于地图构建法[1]，人工势场法[2]和基于随机采样方法。人工势场法是在目标的引力和障碍物的斥力作用下驱动。机械臂，得到运行路径。该方法容易在新环境扩展，但是机器人可能会陷入到局部最小值，同时当面对较多障碍物时，计算量会变得很大。基于地图构建法是将机器人的工作空间划分为不同的网格空间，然后在划分的网格空间中按照一定的规则找到可行路径，主要分为路标法[3]和栅格法[4]。基于随机采样的方法主要分为两种方法：概率地图法（Probability Road Map，PRM）[5]和快速扩展随机树法（Rapidlyexploring Random Tree，RRT）[6]。两者之间的主要差别是RRT算法中的新节点是在随机树中距离该节点最近的节点的相连接；而概率地图法在查询阶段中产生的新节点是与一定范围内所有的可连接节点相连接。因此PRM算法产生的地图会更加复杂。

RRT算法的工作流程比较简单。以自由空间中一个初始点为根节点，采用随机采样的方法进行扩展，生成无碰撞的随机扩展树。当扩展树不停生长，在自由空间中逐步覆盖，最终会得到足够靠近终点的节点，从而生成从初始到目标的路径。RRT算法自身有计算简单，适用于多维空间的优点。很多文章证明利用该算法可以实现在二维空间甚至高维空间的路径规划，因此这种方法可以应用于机械臂的路径规划。当机械臂为冗余机械臂时，其逆运算过程会很复杂，消耗大量时间。因此在更高维度的关节空间内进行路径规划是一种需求。利用RRT算法及改进算法可以在机械臂的关节空间中进行机械臂的路径规划，避免了大量的逆运算，提高了工作效率。

1 基本RRT算法

RRT算法作为一种基于随机采样的空间搜索算法，最大的特点就是简洁，高效。它是在确定初始状态和终点状态的基础上，随机树在自由空间中通过采样、扩展，最终完成搜索，得到一条从初始状态到目标状态的安全可行路径。RRT算法实现简单，不需要对障碍物进行精确建模，在高维空间中任有良好的工作效果。因此，该算法被广泛应用于移动机器人和多自由度串联机械臂的路径规划。其伪代码如算法1所示。

在算法中，qs是起始点，qG是终点，λ是生长步长，T是随机树。

在算法1中的几个主要函数，是RRT算法的重要组成，而且在后面介绍的改进算法中仍有利用。下面对这几个函数进行说明：

GetRandomNode()，采样函数：在自由空间中随机选取一个采样节点qrand。采样点之间的生成是相互独立的，一般情况下是在空间中进行均匀分布采样。

NearNeighbor()，最近点函数：对于已经产生搜索随机树，求取随机树中离函数输入节点q最近的节点qclosest。利用以下公式：

StearNode()，扩展函数：是指从自由空间中的节点q1向另一节点q2方向扩展步长λ，生成新的节点。其公式为：

ColionFree()，碰撞检测函数：对两个节点之间生成的路径进行碰撞检测，以确定两点之间的路径是安全的。若不产生碰撞，两节点之间可以产生路径并返回可行逻辑值。

GettheGoal，到达判定：当随机树的新节点生长到目标节点附近时，则判定到达目标，否则继续继续进行循环操作。

2 改进的快速搜索随机树算法

基于RRT算法的改进算法有很多，相当一部分应用于平面的移动机器人，但很多对于串联机器人有着很高的参考价值。Frazzoli等人利用对路径重构，提出了RRT*算法，使得得到的路径具有渐进最优特性[7]。并且，在RRT*算法的基础之上，Nasir等人提出了具有智能采样和路径优化功能的RRT*-smart算法[8]，解决了RRT*算法中收敛速度慢的问题。还有为了改进在 狭窄复杂环境下规划效率而采用的多向随机树扩展改进[9]。随着机器语言的发展，也出现了与智能算法相结合的采样改进。Shiarlis等人提出的RLT*（Rapidly-Exploring Learing Trees）算法[10]，降低了反向强化学习计算开销。同时还有一些利用神经网络的学习能力与快速搜索随机树算法相结合，进行路径规划的算法[11]。

本文提出的Gm_RRT算法不仅适用于二维空间，同样在高维空间内有着较快的运行速度与运算效果。该算法的改进点主要有以下三个部分。

首先，本文提出的改进算法和常见的几种改进快速搜索随机树算法一样，采用了概率偏置策略，即会以一定的概率将目标点设置为随机采样节点qrand，加速搜索随机树向目标点扩展，提高效率。

其次，由于每次产生新节点都会进行碰撞检测，如果发生碰撞，会舍弃新节点并选取新的随机采样节点qrand，需要重新计算随机树中各个节点与新随机采样节点的距离。此时产生新节点的过程基本上是随机的。而本文中可以对随机点产生过程进行干涉处理，保持了随机树生长的随机性与生长的合理性。采用的方式是在保证采样过程是在随机的基础上，一次采样一组随机采样节点，并以采样节点到目标点的距离由小到大来进行排序，如下面图1所示。当发生碰撞而随机树无法进行扩展，就以次距离的采样节点为方向进行扩展，由此来重复以上工作。当能够扩展新的节点或者随机采样节点组为空时，会重新开始新的采样。

图1 Gm-RRT算法中随机点数组的产生和排序

最后就是引入自适应的引力势场[12]。改进算法是结合了RRT算法和人工势场法的优缺点后，提出了在目标点处设置引力势场。通过在目标点处设置虚拟引力势场，由此来引导随机树趋向目标节点生长，生长的过程如图2所示。而影响生成节点的引力势场大小也会随节点的生长条件发生改变，主要是机械臂末端位姿和目标位姿的差距和机械臂和障碍物之间的碰撞情况。该算法也因此具有自适应的特点。

图2 Gm-RRT算法节点的产生

算法中向目标点生长的引力比例系数为kd，当搜索树生长发生碰撞时，会采用次距离的采样点，同时改变引力比例系数的大小，使随机树的生长偏向当前随机采样点的方向。这样，能够让随机扩展树的生长过程仍保持着向自由空间探索的趋势。

伪代码中，kp是目标引力源对节点产生引力的比例系数。结合式(1)，可得新算法中的节点扩展公式为：

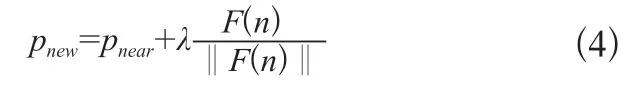
其中：

在经过Gm-RRT算法对机器人的路径点进行规划后得到的路径点，由于新算法是依赖于RRT算法进行的，在计算过程中会出现随机的路径情况，在局部的过程中也可能会出现路径点波折的情况。因此，在算法中加入对机器人的路径一定的优化是不可或缺的一部分。

在常见的路径优化方法中，有一个方法是利用三角形两边之和大于第三边的规律，由路径的终点逐步向前寻找合适的路径。在该过程中，得到的路径可能会出现较小的转角，这对机器人的运行并不是友好的。在本文中，优化的过程是选用弹性带理论，对得到的路径进行优化处理。而且利用弹性带原理在计算中需要的计算量是比较少的，运算的效率会比较高。

弹性带理论最早的提出是为了解决旅行商问题的一种方法[13]。在这里，我们可以将得到的路径看成是一条具备弹性的带子，路径点是受到了整条带子能量的影响而产生形变。

弹性带原理中的能量函数为：

而弹性带上点的受到的力的迭代公式为：

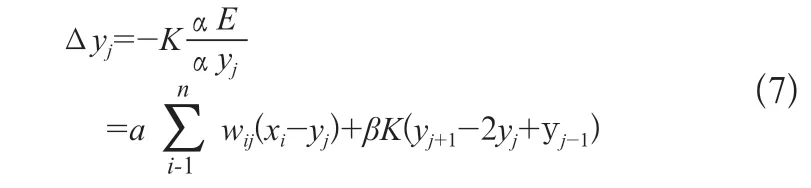
在本文中已经利用RRT算法运行得到了机器人的可行路径，在当我们接下来弹性带原理对得到的路径进行优化处理，此时为了加快运算的效率，我们这里可以将路径节点的“受力”情况分析为：

那么可以设计当路径节点受到的力超出一定范围时，就可以认为节点是受到周围节点的影响的，在受到弹性力的基础上，节点会发生移动，描述方程为：

在算法的最后对机器人运行路径进行优化的时候仍旧需要对机器人在运行过程中的可能产生的碰撞进行检测。以保证机器人运行的安全。

经过前文的分析，可以得到新算法Gm-RRT算法的伪代码如下算法2所示：

3 实验仿真

本节中，我们将会利用新算法进行路径规划仿真实验，以验证新算法的可行性。

3.1 在二维平面的仿真分析

本文中实验的搭建基于MATLAB平台，文中分别利用RRT算法，RRT*算法和改进Gm-RRT算法在平面中进行路径规划的仿真分析，验证了算法的有效性。仿真环境硬件信息：计算机CPU为Intel Core i7-7700，GPU为GTX1060，内存容量为8G。实验参数设置：偏置概率为P=0.2，步长设置为15。对于改进算法中，将采样点个数设置为3，初始kd值设置为0.3，其值依照算法依次递减0.1。为了使算法的运行环境更加客观，本文中采用的仿真地图有两个，分别为简单环境地图和复杂环境地图。

如图4所示，地图中的黑色区域为障碍物，地图的大小为，两张地图中，起始点坐标为(50，50)，终点坐标为(950，950)。其中，红色线条即为算法得到的轨迹。

图4 RRT算法与其改进算法在平面环境的仿真分析

为了将得到的结果与数据显示的更加清晰，本文在经过多次重复试验后将相关数据统计和整理，得到表的结果，这样可以显得更加直观。

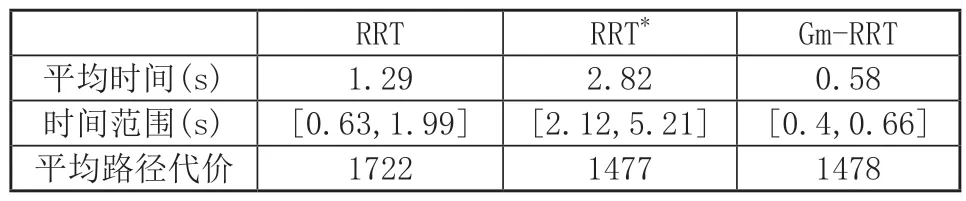
表1 RRT算法与改进算法在场景一的仿真统计

表2 RRT算法与改进R算RT法 在场景R二R的T*仿 真统G计m-RRT

从统计的结果可以看出，改进算法在机器人的路径规划中的表现是比较符合预期的。Gm-RRT算法符合RRT算法的优点，并在一定程度上体现了自己能对不同环境进行适应的特点。

3.2 冗余机械臂的路径规划仿真

本文中进行路径规划仿真的机器人为库卡的LBR iiwa14工业机器人。该款机器人为七自由度冗余串联机器人，该款机器人在工业上具有较为广泛的应用。该机器人具体的DH参数将在表3中给出。图5中显示了机器人的模型与关节的坐标。

图5 机器人iiwa14的模型与关节坐标信息

表3 冗余机械臂iiwa14的DH参数

本文进行实验的平台是基于MATALB平台的Robotics System Toolbox工具箱，该工具箱提供设计、模拟和测试机械手、移动机器人和仿人机器人的工具和算法。对于机械手和仿人机器人，工具箱包括碰撞检查、轨迹生成、正向和反向运动学以及使用刚体树表示的动力学的算法。对于移动机器人，它包括映射、定位、路径规划、路径跟踪和运动控制的算法。工具箱提供了常见工业机器人应用的参考示例。它还包括一个商用工业机器人模型库，工程师可以导入、可视化和模拟这些模型。

路径规划的计算过程中，部分过程是需要利用到机械臂的运动学，以计算机械臂的末端和各个臂杆在工作空间中的位姿。由表3给出的机器人DH参数，进行计算，得到各个刚体连杆的位姿。式(6)中nTn+1是n+1关节相对于n关节的齐次变换矩阵。

对机械臂相邻的坐标系进行连续的坐标变换，可以得到末端杆的相对于机器人基坐标系的变换矩阵为：

机械臂末端的位姿表示为x=[rT，ψT]T∈R6，其中表示末端相对于惯性参考系的位置，ψ是末端对应于惯性参考系的姿态，这里ψ是用x-y-z欧拉角的顺序进行表示的。在这里对机器人的运动规划仿真设置如下：机械臂的基坐标系与参考坐标系重合，且起始状态末端点的位姿是 x1=[-1.40，0.04，-3.05，0.5，0.61，0.18]，最终状态的末端点位姿是x2=[1.02，0.58，-1.06，-0.61，0.68，0.58]，障碍物为蓝色立方体，大小为0.2×0.4×0.6。在路径规划过程中的步长设置为0.8。

在已知起始状态和终点状态末端点位姿的情况下，先利用MATLAB中Robotics System工具箱求逆解，得到这两个状态下机械臂的关节值。将求得的关节值作为关节空间的起始点和终点。机器人关节起点为Q1=[0.95，1.36，-0.2，-0.6，0.18，1.1，-0.9]，终点是Q2=[2.3，1.38，-0.16，0，0.17，-0.23，-0.94]。利用Gm-RRT算法在关节空间对机械臂进行轨迹规划，主要的运行步骤即如第二小节所示，最后得到了机器人在设置环境中规划的路径。

机器人在运行过程中，在对机器人规划得到的路径如果不够柔顺，机器人在工作过程中关节会出现明显的顿挫，那么机器人在经过长时间的工作后会对关节的机械结构造成较大的影响。若将得到的机器人路径在不进行柔顺处理的基础上直接连接运行，那么从数学上看其导数是不连续的，也就是运行的速度和加速度都是不连续的。因此，在本文可以利用B样条曲线对机器人的运行轨迹进行拟合，使得机器人轨迹更加柔顺，运行更加安全。

样条曲线最早源自于在工程制图中利用可变形的条状工具绘制光滑的曲线。而B样条函数曲线可以利用函数进行准确描述的一种样条曲线，具备局部支撑性和集合不变性等优点，因此在工程中会被广泛地应用。将其应用到机器人运动规划的最大优势是对于K次的B样条曲线，其导函数是K-1次连续的。这也就是指机器人的轨迹在利用较高阶B样条函数拟合后，其速度和加速度函数可以是连续且可导的。以此来延续机器人结构的使用寿命。K次B样条的曲线的描述公式为：

式中，Nj，k(u)(i=0，1，…，n)表示的是样条曲线的基函数，dj(j=0，1，…，n表示的是样条曲线的控制顶点。基函数由德布尔-考克斯（Cox-de Boor）递推公式求得。自变量u是经过归一化处理的时间向量节点。在这里为了保证样条曲线是经过路径的起始点和终点，需要在自变量的首尾均设置k+1的重复度，即u0=u1=…=uk=0；un+k=un+k+1=…=un+2k=1。基函数的推导公式为：

之前已经利用改进RRT算法对机器人的路径进行了运动规划，已经得到了期望的一些路径点，此时利用已知的路径点反求对应B样条曲线的控制点，这样不会错过已设好的路径点。

由B样条曲线函数可以得到，若设已知曲线路径对应节点个数为m+1，其控制顶点的个数为d+1，那么两者之间的关系为：

此时，我们已经利用RRT算法求得了机器人关节路径点，此时求取曲线控制点仍缺少k-1个方程，此时，需要加入关节首尾速度与加速度的约束条件即可。可以写为：

在这里，根据实际的情况，可以将机器人初始和终止状态的速度和加速度都设置为零。即v0=ve=0；a0=ae=0。此时就可以得到足够数目的约束方程，就可以求出对应的控制点。

当机器人在有障碍物的环境中基于改进RRT算法进行路径规划后，在利用B样条曲线进行拟合，得到了对应的机器人的柔顺关节路径，其结果如图6所示，机器人关节按照样条函数进行运动控制，那么在运行过程中就可以减少运动中抖动对其产生的伤害，做到延长其寿命的目的。

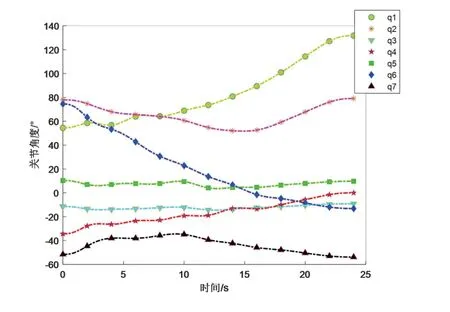
图6 机器人运动柔顺处理后的关节曲线

仿真运动过程如图3所示。从一系列图中，我们可以明显看到，机械臂从初始位置开始，沿着新算法得到的轨迹，绕过蓝色障碍物，最终到达指定位置。平均耗时约7.6s，说明了新算法在高维空间进行路径规划的可行性。

图3 弹性带节点受力分析

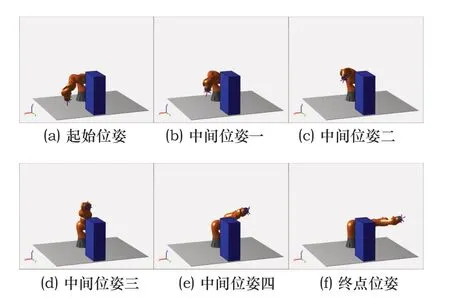
图7 冗余机械臂在有障碍物环境中的运动过程

在基于MATLAB平台对冗余自由度机器人iiwa14进行运动规划仿真，采用了基于改进的快速搜索随机树算法，并且利用了B样条曲线函数对得到的路径进行了柔顺处理。在经过仿真实验后可以看到新算法在机器人的关节空间中进行运动规划的可行性，且得到的运行路径也是比较符合预期的效果。

4 结语

本文研究了冗余机械臂的路径规划算法，提出了基于快速搜索随机树算法的改进算法Gm-RRT算法。首先该算法能够在平面环境下适应不同的环境，体现了自身的特点和优点。同时在机械臂的避障路径规划中，在关节空间中进行了路径规划，得到了较好的路径轨迹。证明了新算法能适用于七自由度机械臂路径规划的特点。该算法在实时性有所不足，也是下一步的改进重点。