基于组合权重的微型机器人可靠性分配方法研究

0 引言

随着人类对地外探索的不断扩展，受发射成本、搭载空间、计划等因素的限制，希望研发出体积小、质量轻的各类探测器，所以近年来，研发轻量化、小型化、刚柔机构结合一体化的微型探测机器人逐渐成为一种发展趋势。微型机器人相比普通移动机器人在体积、质量等方面具有优势，但是目前国内外针对微型机器人主要是在其材料、结构和运动功能等方面的研究[1～4]，对微型机器人整体的可靠性研究较少，然而地外环境复杂多变、又难以全面预知，这样就要求微型机器人在进行地外作业时具备性能的高可靠性，因此，迫切需要运用可靠性分析技术在微型机器人设计初期就进行可靠性分配，以适应复杂恶劣的作业环境。

可靠性分配方法在产品设计初期，其分配方法的准确性将会直接影响到产品内在可靠性[5]。目前，传统机械系统可靠性分配方法主要分为简单分配法和优化分配法，简单分配法对影响因素进行量化赋权，然后分配给各个部分，例如AGREE分配法、故障树分配法等[6，7]。优化分配法通过建立优化模型，将可靠度分配转化为优化问题来求解，例如拉格朗日乘数法、动态规划法等[8，9]。但是，这些方法都有分配效率低、单一赋权方法过于片面且粗糙、影响因素具有局限性等缺点。针对传统分配方法的局限性，文献[10]针对风力发电机组，提出利用改进模糊层次分析法和改进熵权法确定组合权重的方法；文献[11]针对数控机床，提出直觉梯形模糊数与层次分析法相结合的综合分配方法；文献[12]针对风电齿轮传动系统，提出模糊层次分析法和copula方法的组合赋权方法。由于确定组合权重时都是采用乘法归一化或者线性加权平均的方法，以上组合赋权时都易造成大者更大、小者更小等赋权不合理问题。

微型机器人相对于传统机械，系统集成性更复杂，要求其整体与各子系统的可靠度协调性更高，为了解决微型机器人可靠性相互协调和传统分配的不合理问题，运用属性层次法和标准离差法确定微型机器人各系统的主客观可靠性权重值，引入矩估计理论建立主客观权重的最小偏差函数，最后获得最优组合权重值，对微型轮式机器人进行可靠性分配。

1 微型可变形轮式机器人可靠性分配方法

为了使微型可变形轮式机器人可靠性赋权更为合理，提出一种能兼容主客观两种赋权方法的新组合赋权方法。选择属性层次法和标准离差法分别计算其主观、客观权重值，在此基础上，引入矩估计理论对主客观权重值优化赋值。

1.1 属性层次法求主观权重值

属性层次法是层次分析法的一种改进，该方法首先对各因素的重要程度进行主观判别，并将判别结果用数值表示，对数值进行处理后可以得到各因素的权重，相对于层次分析法，它通过定量的方式分析不易量化的问题，省略了特征向量和一致性检验，计算更方便有效[13]。

属性层次法基本理论如下：

1）建立层次结构

层次结构包括目标层A、准则层B和对象层C，假设准则层B中含有m个元素，对象层C中含有n个元素。

2）属性判断矩阵和权重的确定

准则层B中含m有个元素l1、l2、l3…ln，比较li和lj(i≠j) 元素之间的相对重要性，得到相对属性测度lij和lij，其需满足以下关系：

由九标度法的比例标度bij比较元素li和lj元素，而相对属性测度lij可由转换公式确定，转换公式如下：

其中，β通常取1或者2，比例标度bij具体如表1所示。

表1 比例标度值

另：当重要性介于bij={1、3、5、7、9}和bij={1/3、1/5、1/7、1/9}之间时，bij取值为2、4、6、8和1/2、1/4、1/6、1/8。

相对属性权重计算：

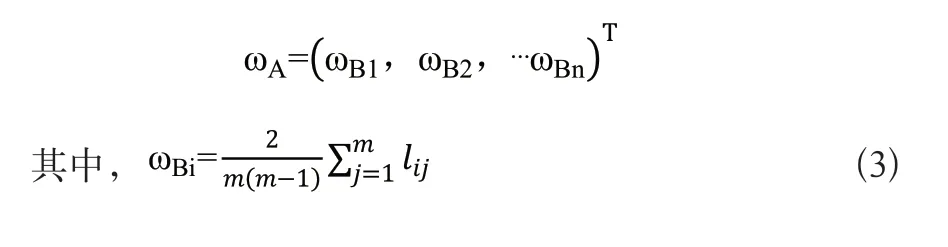
相对属性判断矩阵U：

3）层次属性综合判断

以准则层的每一个因素为新准则，通过式(2)和式(3)建立与它有关的对象层相对目标层的属性判断矩阵和相对权重，则相对属性权重矩阵为：

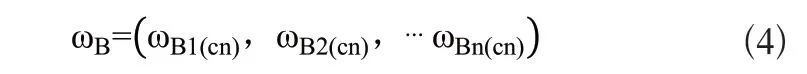
则对象层对目标层的综合权重为：

1.2 标准离差法求解客观权重值

标准离差法是根据指标数据的标准差为依据，若标准差越大，则该指标的变异系数越大，其所赋的权重也应该越大[14]。

1）初始判断矩阵归一化

建立初始判断矩阵，

其中，m为准则层评价指标的个数，n为对象层的个数，kij为第j个因素影响下的第个对象所对应的评价值，对其进行标准化处理，得到标准化判断矩阵T。

2）计算变异系数和客观权重值

通过式(6)计算变异系数，

通过式(7)计算第j个指标的权重，

1.3 求解组合权重值

1）矩估计理论确定最佳组合权重值：

矩估计理论是由英国统计学家Pearson K于1894年提出，根据样本矩来估计总体矩的“替换”思想所建立的预估方法[15]。假设分别有X种主观赋权方法和Y种客观赋权方法，所有赋权方法得到的权重都已满足归一化和标准化，若分别从主、客观权重总体中分别抽取X、Y个样本，则对任一指标Uj(1≤r≤m)而言，其权重与X+Y个主客观权重偏差最小时才最优，用α表示主观权重的重要程度系数，用γ表示客观权重的重要程度系数[16]，即：

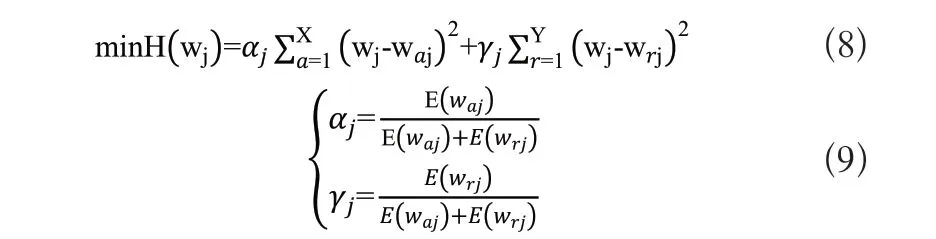
其中，waj和wrj分别为第a种1 ≤ a ≤ X 主观赋权和第r种(1≤r≤Y)客观赋权方法，E(waj)和E(wrj)分别为主、客观权重的期望。

。

则最终的主观、客观权重的重要度系数和为：

组合优化模型为：

通过求解式(11)求出最佳组合优化权重，

2）乘法归一化求解组合权重值

以属性层次法和标准离差法所求解的主观、客观权重数据为基础，利用乘法归一化思想，得到乘法归一化组合权重值，求解公式如下所示。

1.4 整体可靠性分配

由可靠度和失效率之和为1可求出失效率λ，然后利用最佳组合优化权重对各子系统进行失效率分配，具体公式如下：

其中，λi为i系统获得的失效率，Wi为i系统获得的权重。

则各子系统的可靠度为：

2 微型可变形轮式机器人可靠性分配

2.1 属性层次法求解主观权重值

本文以文献[4]的微型可变形轮式机器人为研究对象，其具有小体积、高空间利用率、2种工作模态等优点，可作为未来地外行星探索的新型探测器载体。该机器人由系统整体、各子系统和零部件三部分组成，各子系统主要是：传动系统、驱动系统、可变形主体系统和控制系统，具体如图1所示。

图1 微型可变形轮式机器人

以微型可变形轮式机器人的整体可靠度为目标层A；选取技术水平、运行条件、运行时间、复杂程度、危险程度，共5种评价指标作为影响可靠性分配的准则层B；以机器人的4个子系统为对象层C进行可靠性分配，建立微型机器人可靠性分配层次结构，如图2所示。

图2 可靠性分配层次结构

利用可靠性分配层次模型和比例标度表1，以及专家评价意见，得到准则层5个指标的权重大小关系和准则层两两比较矩阵，权重大小关系如表2所示。

表2 评价指标权重大小关系

指标两两比较矩阵Z如下：

运用式(2)对矩阵进行属性转换，获得属性判断矩阵U为：

运用式(3)可求得准则层相对目标层的权重值向量ωA为：

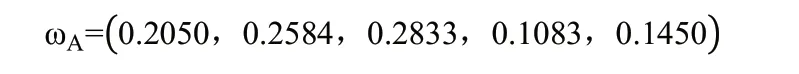
以准则层的每一个因素为新准则，通过专家对微型机器人4个子系统在准则层每个影响因素下进行权重大小打分，得到子系统在单一因素下的权重大小排序，如表3所示。

表3 子系统在单一因素下的权重大小排序

其中，C1为可变形主体系统，C2为传动系统，C3为驱动系统，C4为控制系统。

通过层次属性综合判断、式(2)和式(3)得到在准则层单一因素下对象层相对目标层的相对属性权重矩阵ωB(ωB1(cn)，ωB2(cn)，…ωBn(cn))，整理如表4所示。

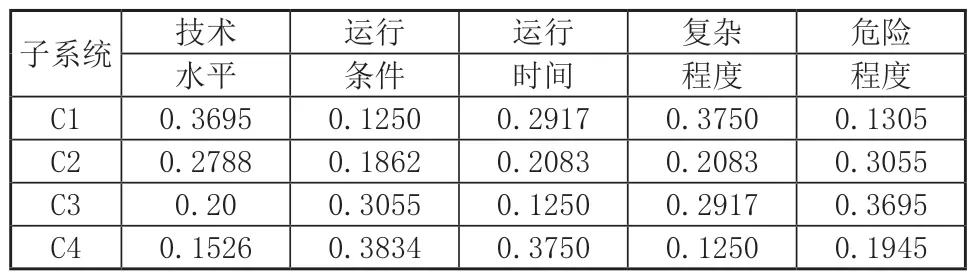
表4 单一因素影响下的子系统的相对属性权重

通过式(5)可计算出子系统相对于机器人整体的综合权重值为：

2.2 标准离差法确定微型机器人客观权重

1）建立初始判断矩阵K，则K=(ωB)T

2）通过标准化将初始判断矩阵K转换为标准化判断矩阵T：

运用式(6)和式(7)得到变异系数和客观权重值，如表5所示。

表5 子系统变异系数和客观权重值

2.3 求解组合权重值

在主客观赋权数据基础上，引入矩估计理论，利用式(8)、式(9)、式(10)求出主观权重的重要程度系数α=0.497、客观权重的重要程度系数为β=0.513，再结合式(11)求解得出微型可变形轮式机器人最优组合权重为：

在主客观赋权数据基础上，引入乘法归一化思想，利用式(12)求出组合权重为：

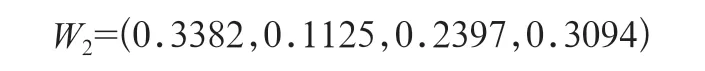
同时，将属性层次法、标准离差法得到的单一赋权值和矩估计理论得到的组合赋权值进行对比，如图3所示。

由图3可以看出，单独运用属性层次法和标准离差法都具有一定的片面性，由W2可知传统的乘法归一化组合方法会造成组合权重大者偏大、小者偏小的“倍增效应”问题，通过矩估计理论对主客观方法进行组合，弥补主、客观赋权方法的不足，同时保留主、客观方法两者对指标的影响，得到的组合权重介于属性层次分析法和标准离差法所得的权重之间，使指标之间的权重偏差明显减小，达到赋权组合的最优化，避免各子系统分配的可靠度出现“薄弱”和“局部过剩”情况，使得赋权结果更合理和公正。

图3 赋权值对比

2.4 整体可靠度分配

取微型可变形轮式机器人整体目标的可靠度为0.95，则微型机器人整体的失效率为0.05，则根据矩估计理论得到的最优组合权重值与式(13)和式(14)得到微型机器人子系统失效率和分配的可靠度，如表6所示。

表6 子系统失效率和可靠度

由于相关资料可知，组成微型可变形轮式机器人的任一一个子系统出现故障，则整个微型可变形轮式机器人都无法展开工作，故，将微型可变形轮式机器人视为串联系统，则整体可靠度R为：

故，运用新提出的组合赋权方法满足可靠度的设计要求，说明方法可行有效。

3 结语

本文针对微型探测机器人的可靠度协调性分配，运用属性层次法进行主观赋权，相比层次分析法，属性层次法不需要确定特征值、特征向量，不需要进行一致性检验，计算更为方便有效。运用标准离差法求解客观权重，排除属性层次法带来的人为主观因素影响。针对传统机械可靠度分配方法中的不合理和乘法归一化方法造成的“倍增效应”的问题，提出一种基于矩估计理论的组合赋权方法，将属性层次法和标准离差法两种方法兼容，使赋权结果更合理公正。该方法可以为微型可变形轮式机器人提供一种简单有效的可靠性分配方法，具有一定工程应用意义。