基于响应面法的安全阀上料车主承重梁优化设计

李天津，朱海清，孔宁宁

（江南大学 机械工程学院，无锡 214122)

0 引言

安全阀的上料过程包括搬运、提升和对中三步，即把安全阀搬运至校验台附近，抬升到校验台上方，并将安全阀中心与校验台中心对齐。目前国内安全阀上料多采用人工搬运或借助行车和叉车的人机辅助搬运[1]。近几年虽然有人提出了几种安全阀上料装备，但应用效果并不理想，文献[1]提出的一种安全阀自动上料机械手可以实现安全阀的提升及对中，但由于不能移动，设备并不能完成安全阀的搬运工作；文献[2]提出的一种安全阀搬运车可以将安全阀搬运至校验台上，但并不具备对中功能，仍需要人工辅助才能完成安全阀与校验台的对中。

针对以上问题本文提出了一种集搬运、提升以及对中功能于一体的安全阀上料车，它能够将DN250以内的安全阀从任意位置搬运至校验台附近，并由对中机构自动将安全阀中心与校验台中心对齐，完成上料工作。如图1所示该上料车主要由行走机构、升降机构、对中机构和夹紧机构组成。其中行走机构的主承重梁是外载荷的承重构件，同时需要开孔装配轴承座与套筒等，受力情况十分恶劣，而主承重梁的过大变形很可能会影响两导杆之间以及导杆与丝杆之间的平行度，进一步加大导杆与滑动轴承之间的磨损，也可能导致升降机构不能平稳运行，甚至卡死。因此，需要对主承重梁进行优化设计，在满足其强度、刚度和尺寸约束的条件下，应尽量减小最大变形量，同时也要尽量满足零件轻量化设计的要求。

图1 安全阀上料车模型

1 主承重梁模型

1.1 结构参数模型

主承重梁的结构参数如图2所示，t1为顶板厚度，t2为侧板厚度，t3为水平筋板厚度，t4、t5分别为内外竖直筋板厚度；P1为顶板宽度，P2为侧板宽度，P3为水平筋板宽度，P4、P5分别为内外竖直筋板宽度。初步选取这10个结构参数为设计变量，设计变量初值如表1所示。

图2 主承重梁结构参数

表1 横梁设计变量初值

1.2 约束及受力模型

主承重梁的约束及受力状况如图3所示，两端标记面B、C与纵梁配合，故施加全约束。主承重梁受到了安全阀及上料车上部机构的重力带来的的弯矩和压力；弯矩作用在套筒上，故将套筒与主承重梁作为整体进行力学分析，可以等效为两个大小相等、方向绕X轴顺时针旋转、作用在套筒内圆柱面上的弯矩M1、M2；压力可以等效为作用在标记面A上、方向竖直向下、大小等于安全阀及上料车上部机构总重的力F；本文静力学分析模拟最危险的工况，即上料车搬运口径为DN250mm的安全阀时主承重梁的受力情况。由于DN250安全阀重约5000N，上料车底盘以上部分总重约1360N，安全阀重心与套筒中心距离为568mm，上料车上部机构重心与套筒中心距离为104mm，故由理论力学计算可求得弯矩M1、M2大小约为1490.72N·m，F2大小约为6360N。

图3 主承重梁约束及受力模型

2 试验设计

为了减少不必要的计算，提高计算效率，同时提高优化模型的精度和准确性，需要通过试验设计对设计变量进行灵敏度分析，筛选出对结构响应灵敏度较高的设计变量。拉丁超立方试验设计比传统的试验设计方法更具填充性与均匀性，是一种覆盖率高、均衡性好的试验设计方法[3，4]。

设计变量的取值范围如表2所示，设计变量的个数为10个，根据拉丁超立方试验设计方法确定样本数为149。通过试验设计计算可以得到如图4所示的各设计变量的灵敏度。图4(a)说明P1，P2，t1，t2，t3对质量影响较大，图4(b)说明P1，P2，P3，t1，t2对变形影响较大，图4(c)说明P1，P2，t1，t2对应力影响较大。所以可将对主承重梁响应值影响较大的参数作为优化设计变量，即选取P1，P2，P3，t1，t2，t3作为优化设计变量，其余参数均保持初值不变。

表2 设计变量取值范围

图4 设计变量对各响应的灵敏度

3 响应面模型的建立

3.1 二阶响应面模型

近似模型方法是通过构建数学模型来模拟输入变量与输出变量之间的关系，在结构优化设计中引入近似模型可以大大加快优化的搜寻速度[5]。二阶响应面模型采用曲面模拟，精确度较高，满足一般工程问题的要求。其表达式为[6]：

式中：y(x)为拟合函数；xi、xj为输入变量；k为输入变量的个数；α0、α1、α2为回归系数，回归系数的个数为：

一般需要m个试验点即可估计出回归系数，其中m≥n；把式(1)写成矩阵形式：

式中：Y=(y1，y2，…ym)T；A=(α1，α2，…αn-1)T；ε为拟合误差，服从正态分布N(0，σ2y)；根据最小二乘法可以得到：

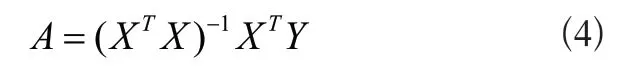
3.2 响应面模型的构建

对于响应面模型的拟合，所需要的最少试验点数等于多项式的项数，但一般情况下样本点越多，响应面拟合得越准确。对主承重梁进行优化时，选择试验设计筛选出的6个设计变量作为输入参数，对于二阶响应面模型，所需的最少试验样本点数为28。拉丁超立方采样能够以少量的样本点拟合出准确度较高的试验模型[7]，为了保证响应面模型的准确度，采用拉丁超立方方法采集样本，样本数为100。将采集的样本点进行有限元分析可以得到相应的质量、最大变形量和最大应力的响应值，代入式(4)可求得回归系数，将回归系数代回式(3)即为响应面模型。

响应面模型的预测能力一般由R2（多重决定系数）和（多重调整决定系数）来评估，通常认为它们的值在0.9～1.0之间时模型的预测能力较好，越接近1.0预测能力越好[8，9]。随机抽取40个样本点进行误差分析，如表3所示，质量M，最大变形Dmax，最大应力σmax的R1和R2a均在允许范围内，且非常接近1.0，说明建立的响应面模型可靠度较高，能够较好的反映输入变量与输出变量之间的关系。

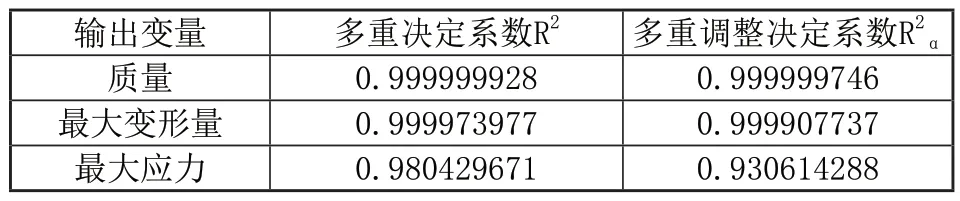
表3 三种二阶响应面模型的R2值及R2a值

式中：yi为试验值，y`为模型预测值，为试验值均值；p为样本点个数；q为回归系数个数。

4 多目标优化

4.1 多目标优化数学模型的建立

根据主承重梁的性能要求，在满足应力要求的条件下，应尽量减小主承重梁的最大变形和质量。以主承重梁的质量M和最大变形Dmax最小为最优目标，最大应力σmax小于材料的许用应力[σ]为约束，建立主承重梁的多目标优化模型：

式中：xi分别为设计变量P1、P2、P3、t1、t2、t3；XL、XU分别为设计变量的上下限。

材料选用Q245R，常温下许用应力为133MPa[10]。

4.2 基于多目标遗传算法求解

传统的多目标优化方法如权重加和法、约束法、理想点法等都是将多目标转化为单目标进行求解，该类方法需要人为确定权重系数或罚值，很可能受主观因素的影响而取不到最优解[11]。多目标遗传算法能并行处理多个目标，鲁棒性强，采用该算法可求解该多目标优化问题。

初始样本数量选取2000个，每次样本迭代数为100，迭代的最大数量为20。图5为优化后获得的最优Pareto解集。由图5可以看出主承重梁的质量与最大变形量是相互矛盾的，最大变形量的减小会伴随着质量的增大。权衡这两个性能指标，从最优Pareto解集中选取一个较优的设计点作为最终设计方案并与优化前的设计点对比。

图5 最优Pareto解集

表4为优化前后各设计变量值对比，表5为优化前后的各参数响应值对比。由表5可以看出，质量增大了1.095%，最大变形量减小了16.89%，最大应力减小了16.04%。结合表4可以看出主要是t1、P3的大幅增大及其余变量的小幅减小引起了各参数响应值的变化，符合灵敏度分析；总体上，优化后的主承重梁除了质量出现了小幅增大外，最大变形量及最大应力均大幅减小，优化效果比较理想，说明了优化方法的可行性。

表4 优化前后设计变量值

表5 优化前后的各参数响应值对比

为验证优化结果的准确性，对选取的最优设计点进行有限元分析，仿真结果如图6所示。将模型预测值与有限元仿真值对比，如表6所示，质量、最大变形量、最大应力的误差分别为0、0.07%、1.26%，误差较小，说明优化结果的准确性较高，也进一步说明了模型预测能力较好。

图6 最优设计点有限元仿真结果

表6 优化后模型预测与有限元仿真响应值对比

5 结语

1）通过拉丁超立方试验设计对结构参数进行了灵敏度分析，筛选出灵敏度较高的设计变量，大幅降低了运算量；采用二阶响应面方法建立了近似模型，模型的多重决定系数R2和多重调整决定系数R2a均在0.9～1.0之间，模型的预测能力较好。

2）利用多目标遗传算法求出了最优pareto解集并确定了最终解，通过与初始设计点的各响应值对比，发现主承重梁的质量仅增大了1.095%，而最大变形量减小了16.89%，优化效果较好。

3）结合拉丁超立方试验、响应面近似模型和多目标遗传算法对主承重梁进行了优化设计，为后续安全阀上料车的稳定性及可靠性研究奠定了基础。