基于车桥振动接触加速度的桥梁频率识别

孙绪法

山东建筑大学交通工程学院 济南 250101

引言

桥梁模态参数包括自振频率、模态振型与阻尼，这些是工程中最有用的信息。采用环境振动试验、强迫振动试验、冲击振动试验等常规方法对桥梁模型参数进行识别，这些方法被称为桥梁测量的直接方法，因为这些方法需要振动传感器直接安装在桥梁上来获得桥梁的响应，且需要安装较多的传感器在桥上。20世纪70年代开始，顺着这些方法进行了许多的研究。此外，桥梁现场监测通常成本高、风险大、耗时长，而在一座桥梁上建立的监测系统很难转移到另一座桥梁上；另一个缺点是各桥梁监测系统连续生成的许多数据无法有效被采纳。

为了解决上述问题，Yang等［1，2］在2004年提出了从一辆仪表化的过往车辆中提取桥梁频率的想法，其中只测试了一阶桥梁频率。现场试验验证了该方法的可行性。与传统的直接法相比，这种间接法不需要在桥梁上安装传感器，只需在测试车上安装传感器，而且间接法具有流动性强、经济、效率高等优点。该技术开发成功后，可用于同一区域桥梁的定期监测，并逐渐发展起来。

最近，Malekjafarian等［3］对2015年之前关于间接方法的相关工作进行了综述。2017年，Yang等提出利用接触点加速度来识别桥梁的动态信息，得到了很好的效果。

1 理论公式

本节主要根据Yang等人2017年发表的《Contact-Point Response for Modal Identication of Bridges by a Moving Test Vehicle》［4］一文，来介绍接触点加速度的理论公式。

图1为车桥动力相互作用模型，实验车辆完全符合理论中的SDOF系统［5］。

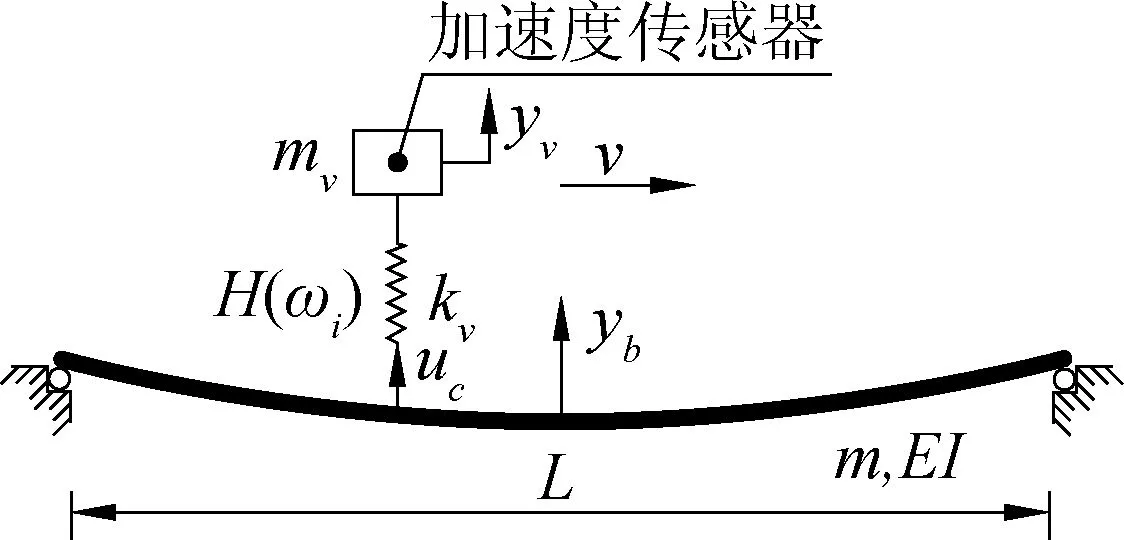
图1 车桥相互作用模型Fig.1 Vehicle-bridge interaction model

图1 中将车辆简化为一个集中质量mv，由一个刚度kv的弹簧支承，以恒定速度v在计算跨径为L的简支梁上移动，其中yb为简支梁跨中竖向位移，H（ωi）为接触点响应与车辆响应之间的关系。车辆为单轴车辆模型，忽略阻尼效应。

车辆的运动方程：

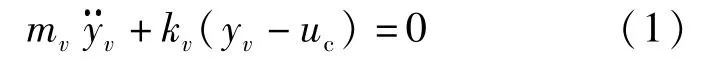
式中：yv是车身的垂直位移；uc为运动车辆与桥梁接触点的位移。

桥梁的运动方程（忽略阻尼作用）：

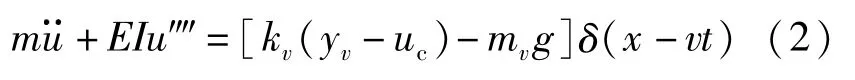
式中：m为单位质量；E为弹性模量；I为转动惯量；g为重力加速度；δ为梁相对于x坐标的微分。

梁的位移可以表示为各个模态响应的和：

式中：qbn是表示梁的模态位移；n为正整数。

车辆频率wv和第n阶桥梁频率wbn分别为：

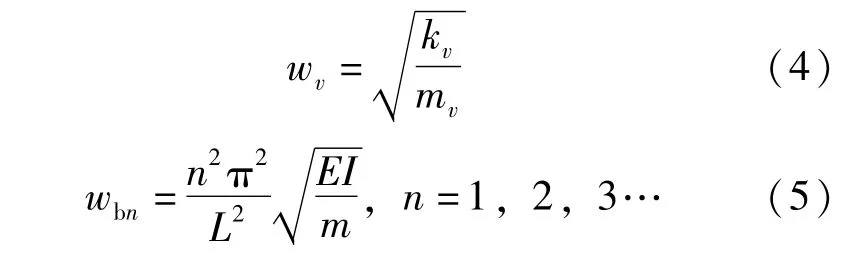
由公式的推导与化简得接触点加速度为：

式中：Δstn近似地表示梁在荷载mvg作用下的第n阶模态静力挠度；sn为速度参数；n为正整数。

由式（6）可知接触点加速度不包含车辆频率，这是一个很好的启示，即在识别桥梁基本信息时，车辆频率被排除外。但是，接触点加速度不能直接测量，所以，可以先得到车辆加速度，通过对车辆加速度进行中心差分，得到接触点加速度。

对式（1）进行对时间的两次微分，考虑到车辆加速度是离散数据，并综合中心差分法得到计算的接触点加速度：

式中：Δt为时间间隔；i为大于1的正整数。

接触点加速度可由式（10）计算得到。

2 理论验证

Yang等［4］采用简支梁获取其车辆响应，并将理论解与有限元解进行对比，验证了接触点加速度响应识别桥梁频率的正确性。本文采用的简支梁具有如下参数：长L=25m，单位质量m=2000kg／m，E=27.5GPa，惯性矩I=0.15m4，表面光滑。车辆mv=1000kg，cv=0，kv=200kN／m。采用以上桥梁参数，建立ANSYS车桥耦合模型，图2为利用式（10）计算出的接触点加速度时程响应，图3为ANSYS软件中提取的车辆加速度时程响应。采用快速傅立叶变换对图2的接触点加速度进行处理，获得频谱图如图4所示，获得的前四阶频率与理论频率非常接近，可知，此方法是可靠的。

图2 接触点加速度时程响应Fig.2 Time-history response of contact point acceleration

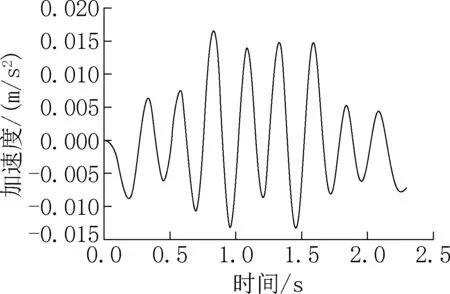
图3 车辆加速度响应Fig.3 Vehicle acceleration response

图4 接触点加速度响应频谱图Fig.4 Acceleration response spectrogram of contact point

3 获得桥梁频率

3.1 桥梁建模

采取车速v=10m／s，在有限元模型中获取提取的车辆加速度响应，通过式（10）计算出接触点加速度，再通过快速傅立叶变换得到频谱图。在Matlab中经过傅立叶变换［6］将时域转变为频域信号，进而获得桥梁的各阶频率。因采集的数据都是离散的数据，故而利用式（11）［7］对离散数据进行处理。

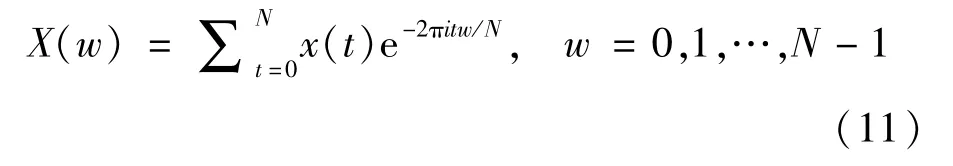
模型的选取位于湖南长沙某市政桥梁，桥梁为跨径23m+35m+23m的连续梁桥，全桥采用C50混凝土，弹性模量E=3.45×104MPa，桥面宽13.25m。桥梁的横截面如图5所示。桥梁基本信息见表1。

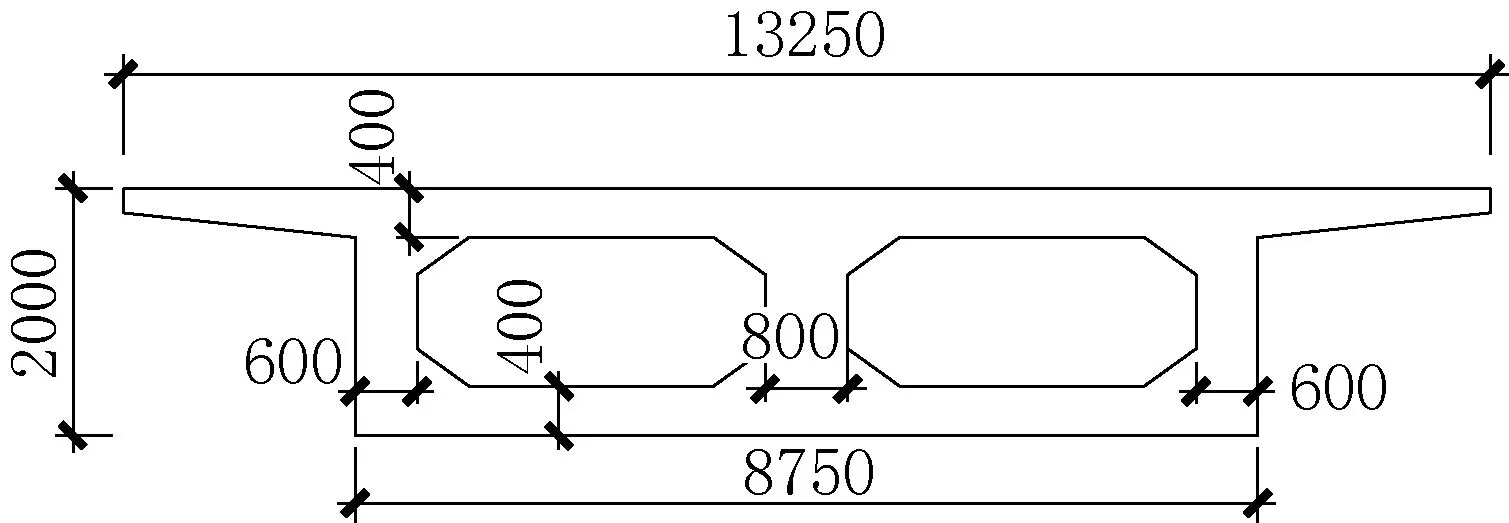
图5 桥梁横断面（单位：mm）Fig.5 Cross-sectional view of the bridge（unit：mm）

表1 桥梁详细参数Tab.1 Bridge detailed parameters

车辆匀速通过桥梁，使用和Yang等［4］同样的单轴车模型，车桥模型如图6所示。图6为一个集中质量mv，由一个刚度kv的弹簧支承，以恒定速度v在连续梁桥上移动。

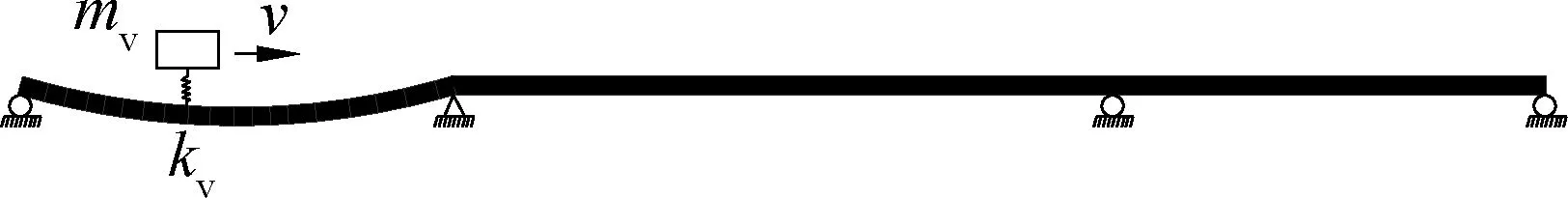
图6 车桥模型Fig.6 Axle model

使用表1中的参数，建立车桥有限元模型，可得到桥梁的动力特性，见表2。

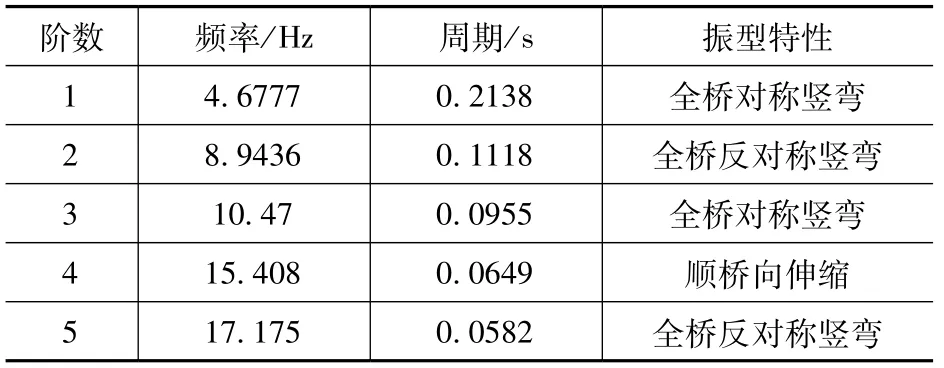
表2 桥梁动力特性Tab.2 Bridge dynamic characteristics

3.2 桥梁频率

接触点识别可以比车辆加速度识别的效果更好、更直观。桥梁频率反应桥梁动力特性［8-10］，在本节中，进行数值计算来比较。

通过式（11）获得车辆加速度频谱图与接触点加速度频谱图，如图7、图8所示。从图7可以看出，除了车辆频率外，在车辆加速度频谱中识别出的前两阶桥梁频率较清晰，而第三、四频率仅是可见的，由车辆加速度识别获得桥梁的第三、四阶频率幅值下降较快。从图8可以看出，接触点谱只包含桥接频率，可以清晰地识别出前四阶桥梁频率。因此，通过接触点加速度识别出的桥梁频率更清晰、直观。

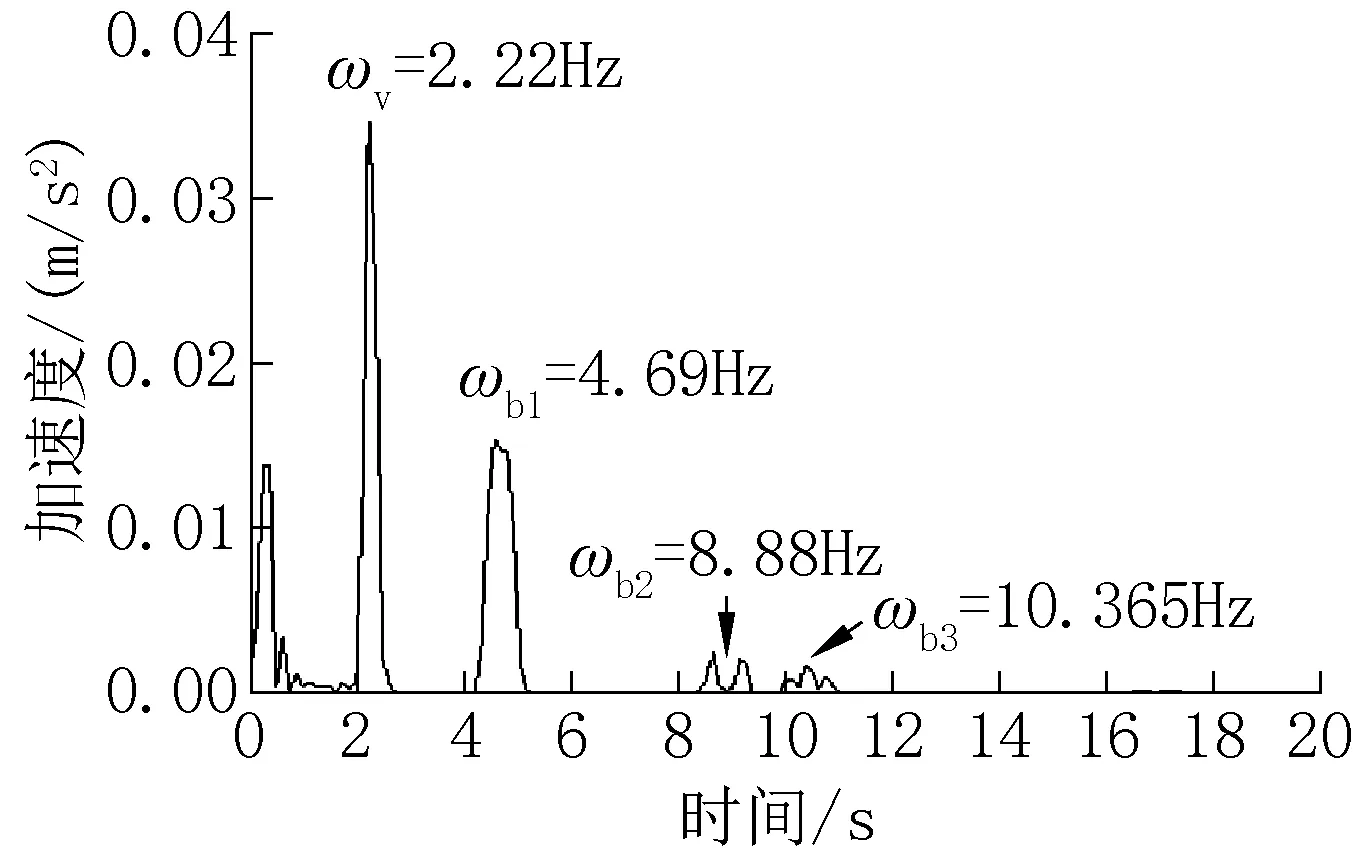
图7 车辆加速度频谱图Fig.7 Spectrum of vehicle acceleration

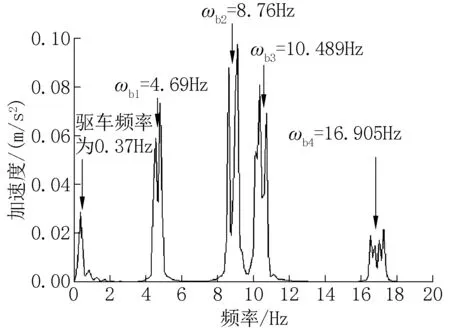
图8 接触点加速度频谱图Fig.8 Acceleration spectrum of the contact point

4 路面粗糙度效应

4.1 有粗糙度、无车流

在平整条件下，识别出的桥梁频率效果都很好。在本节中将添加粗糙度来探究接触点加速度的识别结果。

粗糙度采用ISO 8608［11］的标准提出的功率谱密度来模拟，此标准把路面的不平度分为八个等级A～H，等级越高路面效果越差，A级最好，H级最差。描述粗糙度的功率谱密度Gd（n）为：

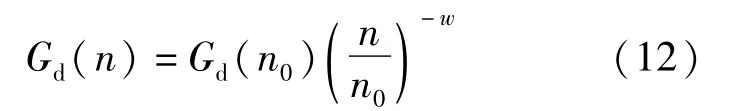
式中：n为空间频率，波长的倒数；w为拟和指数其数值为2；n0为参考频率。本文采取A级粗糙度，如图9所示。

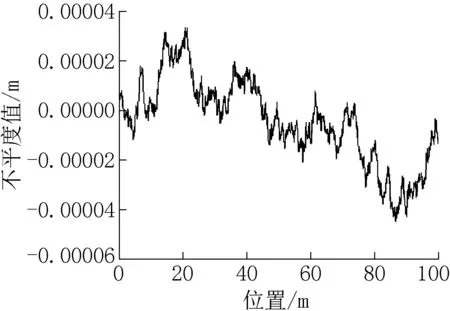
图9 粗糙度Fig.9 Roughness

1t小车过桥，粗糙度引起接触点跳动，通过式（11）获得接触点加速度频谱图，如图10所示。由图10可见并不能清晰地识别出桥梁频率，小车质量过轻，过桥激振能量不够，激励太小，所以无法清晰地识别出桥梁频率。

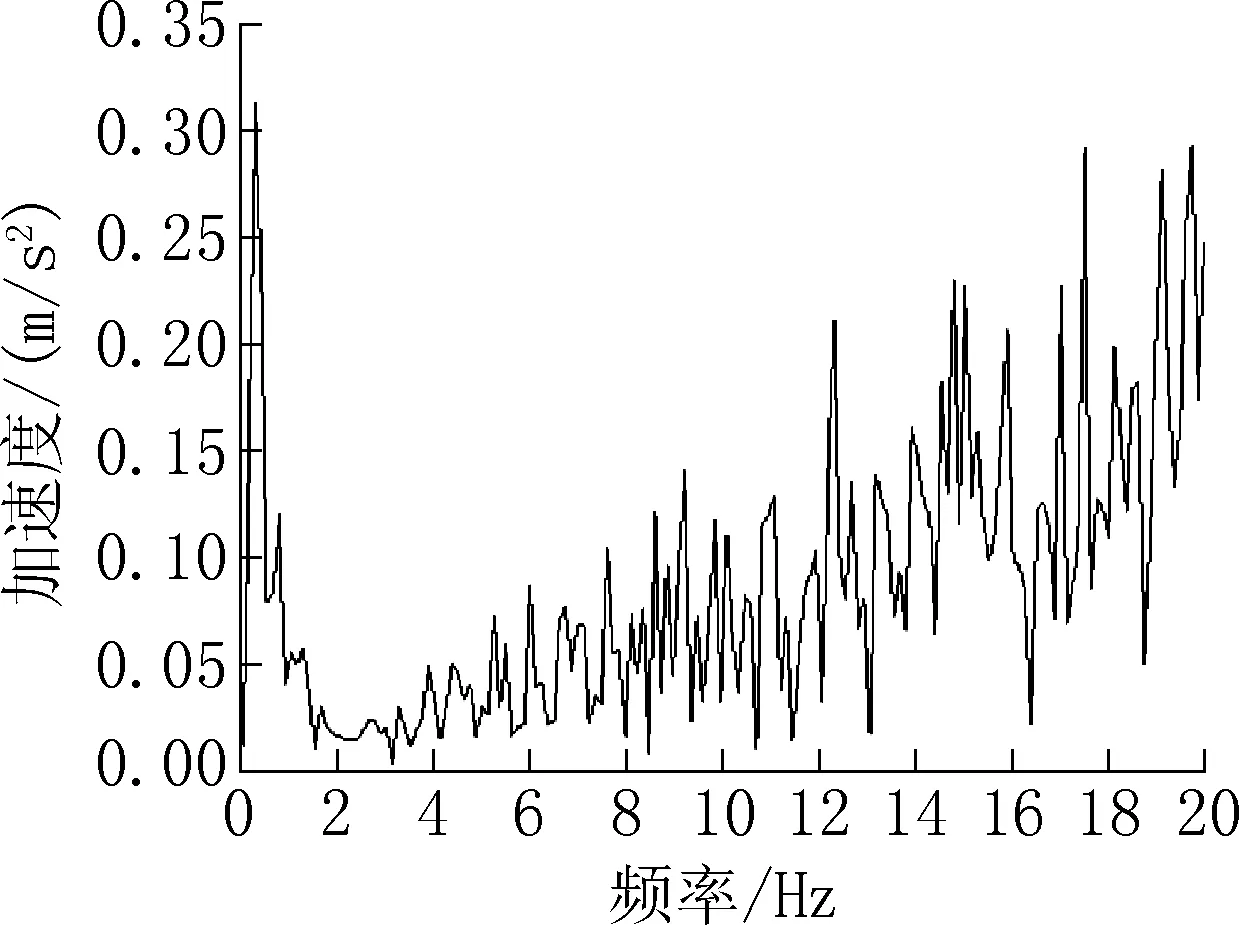
图10 粗糙桥梁接触点加速度频谱图Fig.10 Acceleration frequency spectrum of rough bridge contact points

4.2 有粗糙度、有车流

从图10可以看出，1t小车经过桥梁，获得的接触点加速度频谱图，并未识别出桥梁频率。现加上社会车流，用一辆卡车代替模拟社会车辆，来刺激桥梁响应。社会车辆15000kg，刚度1350kN／m。

从图11中可以看出，加了社会车流，可以刺激桥梁获得更大的响应，可以得到桥梁的前二阶频率。

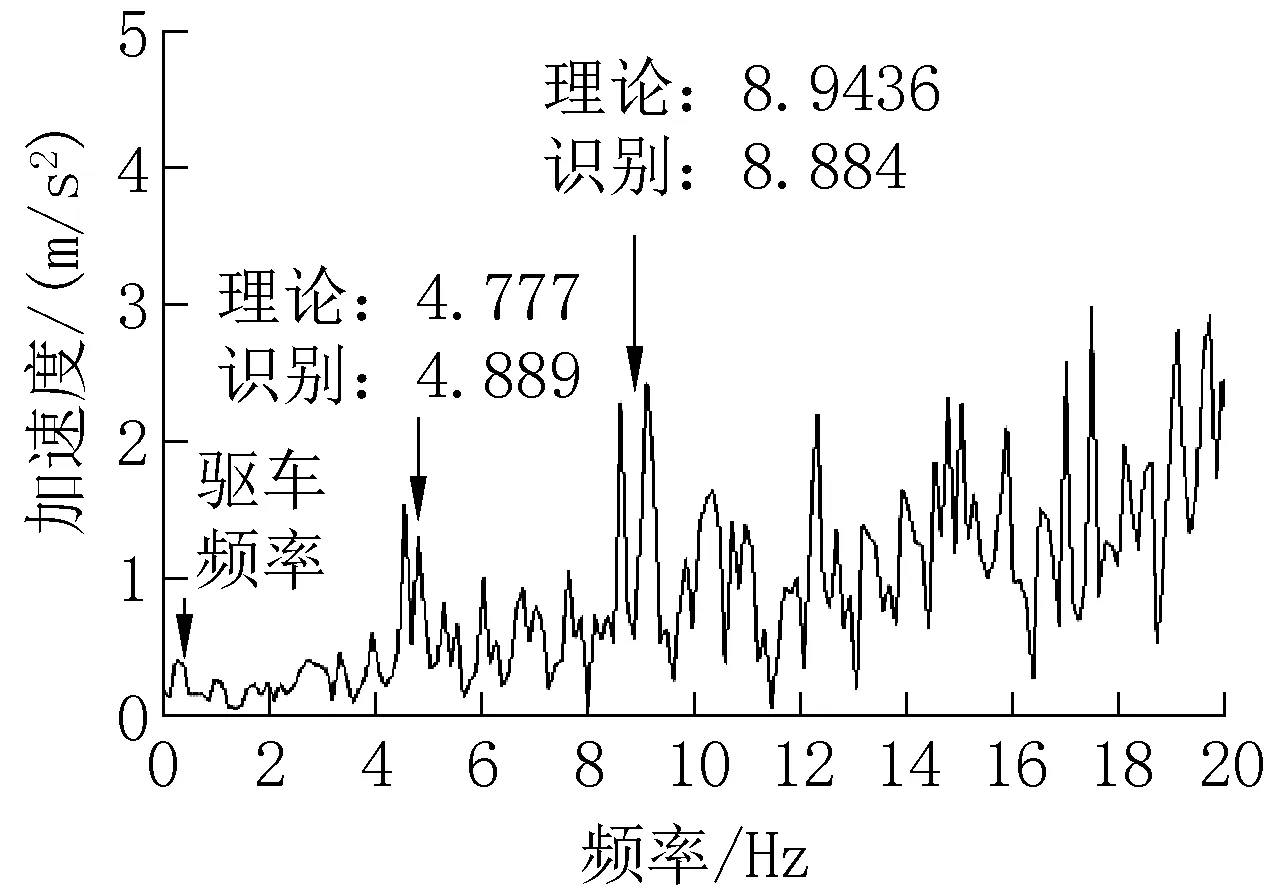
图11 有车流粗糙接触点加速度频谱图Fig.11 Acceleration spectrum of rough contact points with traffic flow

5 结语

本文通过数值模拟得出以下结论：

1.在路面平整情况下，利用接触点响应比车辆响应得到的桥梁频率更清晰、更直观，且不受车辆频率的干扰；

2.在路面不平整情况下，结合现有交通可以更好地识别出桥梁频率，但相比于平整情况下，识别效果变差。通过现有交通，可以刺激桥梁响应。