风力机叶片翼型气动性能对比与分析

于新青 何永玲* 黄芳武 吴 飞 胡 凯

(北部湾大学机械与船舶海洋工程学院1) 钦州 535011) (武汉理工大学交通学院2) 武汉 430063)(桂林电子科技大学机电工程学院3) 桂林 541004)

0 引 言

海上风电是可再生能源，具有风能资源稳定、不占用土地、消纳条件良好等独特优势[1-2].风力机叶片是使风能转化为机械能的主要构件，直接关系到机组的风能利用效率和气动载荷，决定着风力发电机组能量转换效率.

叶片由翼型按照一定规律叠加而成，翼型的气动特性直接影响风能利用效率.刘丽娜等[3]通过Profili与Fluent接口衔接方法，确定了翼型气动模拟方案，在此基础上开发了风力机翼型建模与仿真一体化系统.吴友健等[4]采用数值方法研究不同攻角时NACA4415翼型的气动特性，利用ICEM对NACA4415翼型进行结构化网格划分，计算结果表明在6°攻角时翼型存在最大升阻比，此时翼型的气动性能最佳，对风能利用率最高.Andrew等[5]对比研究了多种不同翼型在低风速环境下的性能，发现NACA4412这种翼型在气动噪声和升阻特性等方面都具有明显优势.代元军等[6]通过对S型翼型绕流流场进行数值模拟，并对比其实测数据，最后证实了S翼型具有气动性能良好的优点.从上述研究中可以看出NACA翼型和S翼型都具有气动性能良好的优点.目前针对我国广西北部湾海域探索性发展海上风电的现状，不同翼型对此海域的适用性探索研究较少.

针对广西北部湾海域在离岸20～40 n mile范围内，100 m高度年平均风速为6.8～7.5 m/s这一特定风速的条件下[7]，选择目前低风速下有代表性的NACA4412和S1010这两种翼型作为研究对象，分别针对这两种翼型进行流动和气动特性研究，并比较其在低风速环境下的性能表现.

1 翼型气体动力学模型

1.1 翼型气动参数

在空气的流场中，气流速度快的区域压力小，气流速度慢的区域压力大.当叶素与大气存在相对运动时，气流在叶素产生了升力dL和阻力dD，阻力与相对速度方向平行，升力与相对速度方向垂直.相对气流方向与叶素翼型几何弦的夹角称为攻角，用α表示.

叶素上的升力为

(1)

叶素上的阻力为

(2)

式中：ρ为空气的密度，kg/m3；ω为相对速度，m/s；c为几何弦长，m；Cl为升力特征系数；dr为叶素的长度，m；Cd为阻力特征系数.

Cl和Cd是描述翼型所受到的力的量纲—的量参数，其中升阻比Cl/Cd是衡量叶片翼型在不同环境中产生升力和阻力的能力的重要参数.升阻比的值越大，说明翼型受到的升力越大，叶片翼型的气动性能越好，叶片能够更好地利用风能来提高发电效率.

2 控制方程和湍流模型

2.1 控制方程

对于低风速风力机绕流，流场中的密度变化很小，因此，可以假设其绕流流动为不可压缩流动.此外，流场中温度的变化不大，黏性系数随温度的变化可以忽略.边界层流体分离和流体的粘性有关，因此在计算时不能忽略流体的粘性.故采用连续性方程和N-S不可压缩方程作为数值模型的流场控制方程

(3)

(4)

(5)

式中：ρ为流体的密度；u为流体的速度；μ为流体黏度系数.

2.2 湍流模型

由于本次计算为外流场模型，壁面附近非常重要，SSTk-ω模型对边界层湍流和自由剪切湍流均有良好模拟效果，是理想的选择，该湍流模型可以求解黏性子层，其运输变量为湍动能k和比耗散率ω，运输方程为

(6)

(7)

式中：Gk为湍动能；Gω为比耗散率，Gω由ω得出；Γω和Γk分别为k和ω的耗散项；Dω为交叉扩散项；Sk和Sω为原项.

3 翼型流场建模与网格划分

3.1 翼型流场建模

本研究总体思路是通过Profili提取翼型数据，在ICEM中建立计算域，经过网格划分，最后导入Fluent中进行计算分析.整体框架图见图1.

图1 整体框架图

Profili软件是专业翼型设计软件，内置翼型数据多达上千种，文中使用Profili翼型库对这两种翼型进行数据提取.通过Profili软件数据库得知NACA4412翼型最大厚度为12.02%，在30%的翼弦位置；最大曲面为4.00%，在40%的翼弦位置.S1010翼型最大厚度6.02%在23.3%的翼位置，最大曲面0.00%在0.0%的翼弦位置.

3.2 流场域的建立与网格划分

根据模拟实际应用，在Profili中选取NACA4412和S1010翼型，输出dat格式翼型坐标点数据.将整理好的翼型数据点导入ICEM中进行网格划分，考虑到单个二维翼型几何形状较为简单，故采用结构化网格进行划分.S1010翼型整体网格分布见图2.

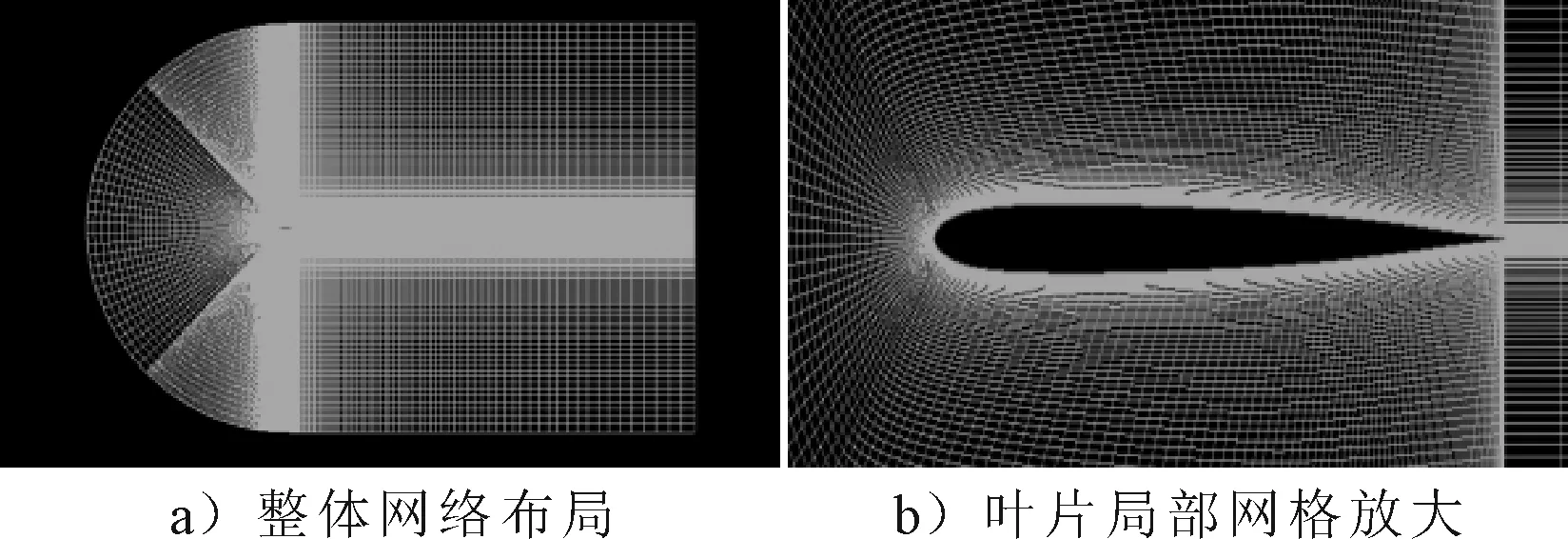
图2 S1010整体网格划分图

将在ICEM中划分好的网格导入Fluent中，并在其中将在边界条件设置为速度入口和压力出口.翼型壁面设置为绝热无滑移壁面边界.选用SST湍流模型，压力-速度耦合采用Simplec算法，压力项、湍流黏度项、动量项均采用二阶迎风格式离散.在计算过程中打开残差监视器同时监测升力系数、阻力系数，当残差最大值小于并且所监测的参数不随迭代次数变化而改变，则认为计算收敛.通过改变风速的来流方向来实现攻角的变化.

4 升阻特性分析

4.1 翼型气动特性分析

选取广西北部湾海域在离岸20～40 nmile范围内，100 m高度年平均风速为6.8～7.5 m/s这一特定风速范围，并在这一特定风速范围下对两种翼型特性进行分析对比.图3～4分别为NACA4412翼型和S1010翼型在7 m/s风速下随攻角α变化的速度云图.

根据伯努利原理，流速大的区域形成负压区，流速小的区域形成正压区.由图3～4可知:随着攻角的不断增大，在0°～12°攻角范围内，翼型尾缘位置出现显著的气流分离，翼型上表面的逆压梯度不断向前缘移动，在翼型尾部区域的气流已经不再紧贴翼型表面来流动了，由层流附着流变为紊流扩散流.

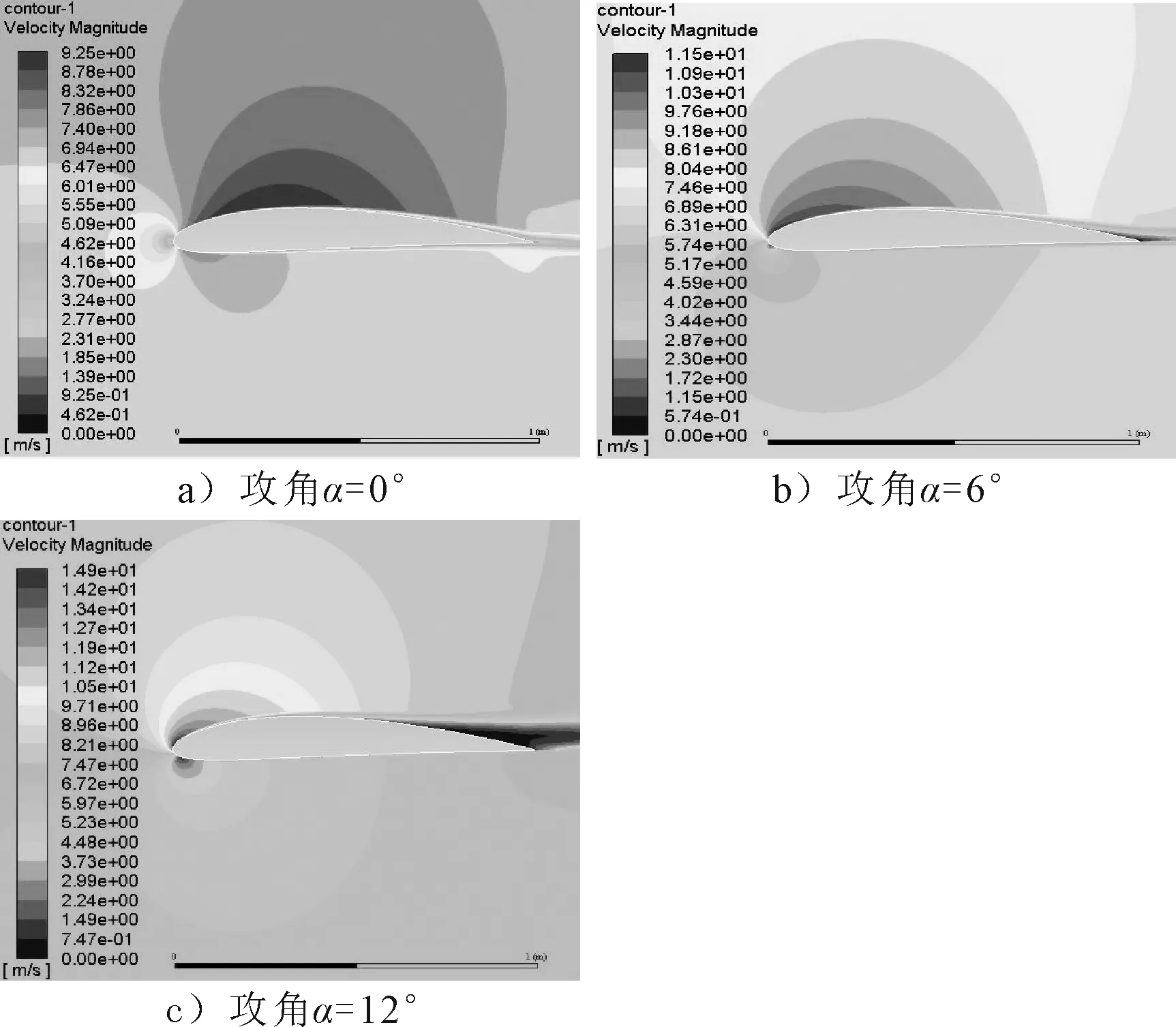
图3 翼型NACA4412速度云图

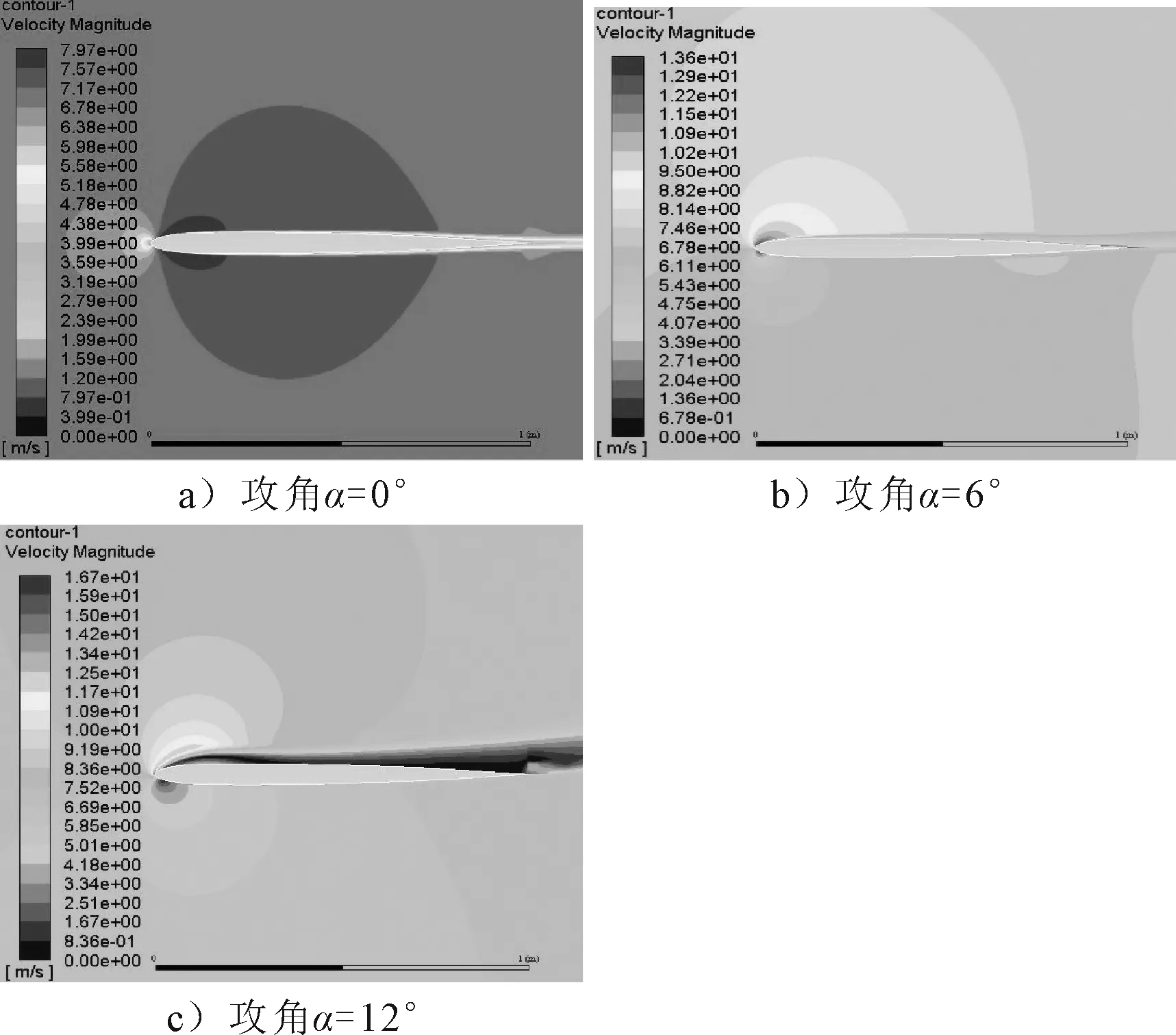
图4 翼型S1010速度云图

4.2 翼型升阻力系数计算及分析对比

为了研究在广西北部湾海域这一特定风况下，攻角变化对翼型气动性能的影响规律及其性能差异，选取6.5，7，7.5 m/s的低风速工况，对这两种翼型在不同攻角下的升阻特性进行数值仿真，并对比分析其升阻比曲线.图5为用Matlab曲线拟合得到的NACA4412翼型和S1010翼型模拟数据曲线，翼型的升阻比随着攻角的增大呈先增大后减小的趋势.由图3～4可知:在小攻角工况下，气流流经翼型表面在翼型尾部还没有发生分离，升阻比随着攻角的增大呈上升趋势；而在大攻角工况下，气流在翼型尾部发生分离脱落现象愈加明显，此时的升阻比呈下降趋势.

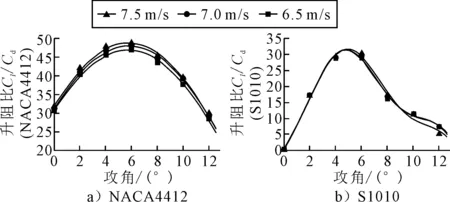
图5 不同翼型升阻比

由图5可知:在6.5～7.5 m/s的风速范围，这两种翼型最大升阻比对应的攻角变化不大，这说明在此风速区间，翼型最佳攻角比较稳定.并且在此风速范围条件下，两种翼型在不同攻角下的升阻比变化规律不受风速变化的影响.分析这两种翼型的在此风速范围内的最佳升阻比以及升阻比变化规律，NACA4412翼型的Cl/Cdmax为48.86，S1010翼型的Cl/Cdmax为30.26.通过对比发现相较于S1010翼型，NACA4412翼型的升阻特性较优.

4.3 数值拟合及数学模型

图6为NACA4412翼型在7 m/s风速下计算所得的7个点坐标运用Matlab曲线拟合的图形，通过Sum and Sine曲线拟合的方法，得到了升阻比曲线图.

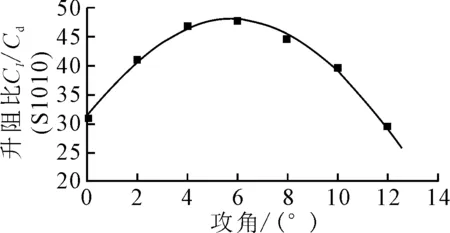
图6 翼型NACA4412拟合升阻比曲线(7 m/s)

拟合升阻比曲线随攻角0°～12°范围内的数学模型为

f(x)=48.1×sin(0.148 3×x+0.710 8)

(8)

图7为S1010翼型在7 m/s风速下计算所得的7个点坐标运用Matlab曲线拟合的图形，通过Custom Equation曲线拟合的方法，得到了升阻比曲线图.

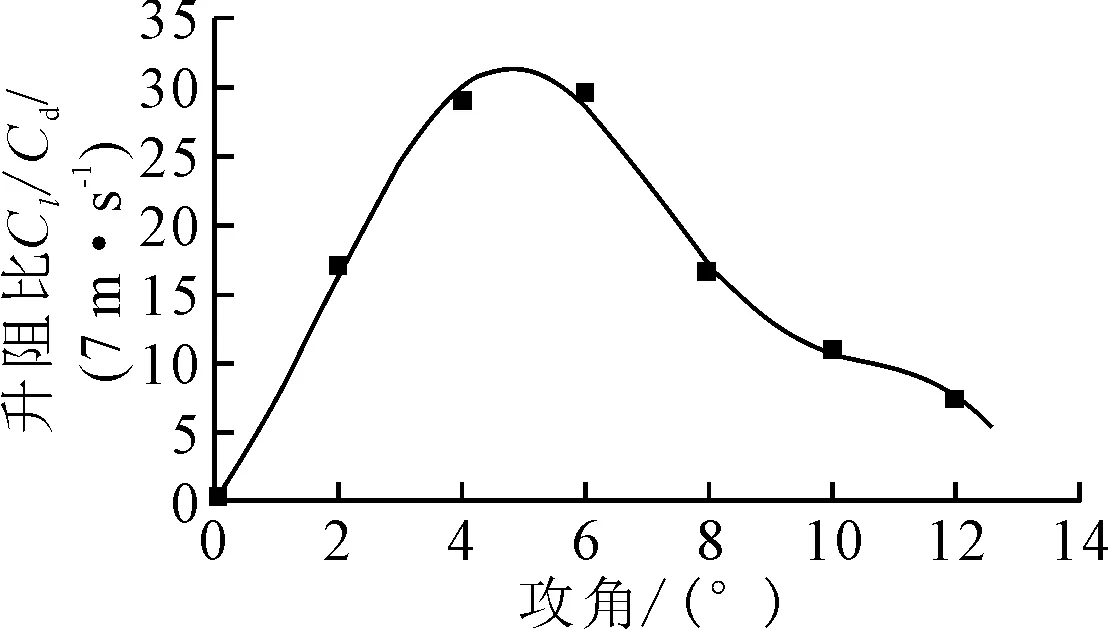
图7 翼型S1010拟合升阻比曲线(7 m/s)

拟合升阻比曲线随攻角0°～12°范围内的数学模型为

f(x)=30×sin(0.21×x+0.35)-

6.29×sin(0.71×x+7.89)-3.96

(9)

5 结 论

1)在广西北部湾海域特定风速条件下NACA4412和S1010两种翼型，两种翼型在不同攻角下的升阻比变化规律基本不受风速变化的影响.

2)非对称翼型NACA4412相较于S1010翼型在相同工况下的升阻比更大，验证了NACA4412翼型更适用于广西北部湾海域的风速环境.

3)通过仿真分析得，随着攻角的增大，来流在两种翼型尾缘发生流动分离，形成涡流，降低翼型的升阻特性；当攻角超过某一临界值时就会出现失速现象，两种翼型在攻角增大趋势中都达到了最大升阻比，此时的气动性能最好，对风能利用率最高.

4)通过Profili软件进行翼型数据点获取，将数据点导入ICEM中进行网格划分，在Workbench中将ICEM和Fluent进行衔接，提高了翼型研究效率.