浮冰区船舶冰阻力数值计算研究
2022-03-12何宾峰詹成胜赵桥生轩慎宇
何宾峰 詹成胜 赵桥生 轩慎宇 国 威
(高性能船舶技术教育部重点实验室(武汉理工大学)1) 武汉 430063)(武汉理工大学船海与能源动力工程学院2) 武汉 430063) (中国船舶科学研究中心3) 无锡 214082)
0 引 言
全球气候变暖造成极地冰层逐年融化,海冰覆盖面积持续减小,影响北极航道通航[1-2].浮冰海况是极地船舶航行将遭遇的一种典型冰况,即便是在夏季通航期,北极航道多处航段都存在冰况不等的浮冰.船舶在浮冰海域航行过程中,易发生船速降低、舵效不佳、操纵困难、船舶的回转圈大幅增加等现象.对于浮冰海域航行的船舶,船体冰阻力的大小不仅取决于船舶的船型和航速,还与浮冰的密集度、厚度、尺寸大小等参数有关.
Cundall[3]提出了一种处理非连续介质问题的数值模拟方法,即离散元方法(DEM).离散元法对浮冰冰块进行几何及物理状态建模,能形象地反应应力场、位移及速度的变化,非常适合于船舶在浮冰区域航行时的运动及冰载荷求解问题.Hopkins[4]将离散元方法引入船舶与破碎冰的相互作用问题,对浮冰区的船、冰作用力进行分析计算.Konno等[5]运用颗粒离散元方法,用二维圆盘和三维圆球建立浮冰模型,求解离散浮冰中航行船舶受到的冰载荷.Lau等[6]运用由块体离散元方法发展而来的商用软件DECICE,计算了浮冰区船舶和浮冰的作用力,验证了离散元方法在处理浮冰问题上的可行性.国内学者对浮冰区船舶冰阻力的研究起步较晚,季顺迎等[7]采用三维圆盘离散元方法,对碎冰区航行船舶的冰阻力性能进行了数值计算研究,得到了不同浮冰参数条件下的船体冰阻力.王超等[8-9]运用离散元模型结合欧拉多相流方法,研究了船体和碎冰之间的相互作用,对冰船碰撞时的运动响应进行了探讨.
离散元方法很好地解决了浮冰的不连续介质特性,能更好地计算船体和浮冰之间的碰撞,是现阶段国际上研究浮冰区船舶冰阻力问题所采用的主要方法.但国内目前在对浮冰区船舶冰阻力的研究中对冰块的建模停留在单个球形颗粒或者单个三维圆盘的结构,研究变量较少,且很少考虑流体作用对冰阻力的影响.在船冰发生相互作用时,冰块的运动将对船体流场有较大的影响,同时流体的流动也会对冰块的运动产生浮托和阻曳作用,忽略流体作用将会对数值结果产生较大的误差.船模试验是一种较为准确的冰阻力预报方法,可以最大程度重现船舶在冰区航行时的状态,但由于成本高、准备时间长,并不适用于初步设计阶段.文中运用EDEM离散元软件,用结构相同的球形颗粒对浮冰块进行建模,考虑流体作用对冰阻力的影响,对船模试验中的不同航速、密集度、厚度和尺寸大小条件下的直航运动进行模拟,分析不同航速和不同浮冰参数条件下的冰阻力特性.
1 数值方法
1.1 基本方程
船在较小尺寸的浮冰区航行时,船冰间、冰块间的相互作用主要体现在碰撞、挤压等行为,冰块主要发生升沉、翻转运动,冰块的破碎现象较少,所以本文将船体和冰块都视为刚体进行数值模拟.水的流动会对冰块产生浮托和阻曳作用,忽略流体作用会对数值结果产生误差,在离散元EDEM软件中,添加水对冰块的浮力和曳力作用.风、浪对冰块的影响较小,在数值计算中忽略自由液面的影响.
以一个浮冰冰块为例,对离散元方法的基本方程进行分析.根据牛顿第二定律,在每一个时间步内,建立冰块的运动方程:
(1)
(2)
式中:mi为冰块质量;ui为冰块形心的运动速度;Fi为对冰块的作用力;Ii为冰块对形心的转动惯性;ωi为冰块的角速度;Mi为冰块作用力产生的力矩.
1.2 接触力
1.2.1接触变量
当两个颗粒或者颗粒-结构体之间发生具有一定重叠量的接触时,通过接触变量表征重叠量的大小,见图1.
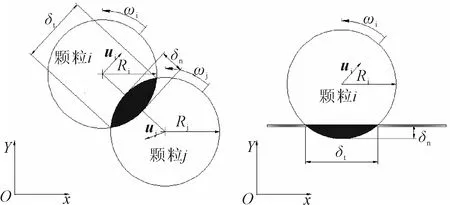
图1 颗粒-颗粒与颗粒-结构体接触时的接触变量
接触变量在二维时为长度量纲,三维时为面积量纲.船体大小远大于冰块颗粒单元大小,当船体与冰块颗粒单元接触时,船体视为半径无穷大的结构体.
1.2.2Hertz-Mindlin接触模型
对于一般的干态、刚性、不发生破碎等变化的固体冰块颗粒及船体,采用Hertz-Mindlin接触模型描述其之间的接触作用力[10].
法向弹性力:
(3)

法向阻尼力:
(4)
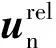
颗粒之间的切向力:
Ft=-Stδt
(5)
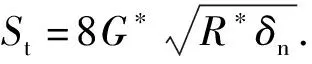
颗粒之间的切向阻尼力:
(6)

切向力合力的最大值受库仑摩擦定律的限制,即切向力的合力不超过最大静摩擦力μsFn,其中:μs为静摩擦系数.
当接触点的两个单元在发生相对转动时,滚动摩擦力将产生额外的力矩作用:
Ti=-μrFnRiωi
(7)
式中:μr为滚动摩擦系数;ωi为接触点的相对旋转角速度.
1.3 曳力和浮力
冰块所受的曳力计算式为
Fdrag=∑kRecAρf|vf-vp|(vf-vp)
(8)
式中:Re为流体雷诺数;A为离散元的网格面积;ρf为流体密度;vf和vp分别为流体与颗粒在离散元的网格处的速度;k为流体曳力系数,取0.627;c为雷诺数系数,取-0.012(k和c的值通过CFD直接数值模拟方法进行标定得到).
冰块所受的曳力产生的力矩为
Tdrag=∑FdragLsinθ
(9)
式中:L为表面网格中心到颗粒质心的矢量长度;θ为矢量F与矢量L的夹角.
冰块所受的浮力计算式为
Fbuoyancy=∑ρgVi
(10)
式中:ρ为水的密度;Vi为冰块浸入水中的体积.
冰块所受的浮力产生的力矩为
Tbuoyancy=∑ρgViLsinθ
(11)
2 计算前处理
选取“雪龙号”破冰船船模作为计算模型,船模与实船的缩尺比为30,船型参数见表1,船模模型见图2.数值模拟过程中,船模进行直航运动,约束船模的升沉及纵摇,忽略重力场的影响.

表1 船体模型参数 单位:m

图2 船模模型图
选取颗粒离散元方法对船模试验中的浮冰冰块进行建模,根据浮冰的材料特性采用球面拟合非球形冰块颗粒外形,相接触的浮冰周边采用较小小球建模,不接触的浮冰内部采用较大小球进行填充,以球面接触代替冰块和冰块之间、冰块和船体之间的复杂曲面接触.在同一工况条件下的每个四棱柱冰块的厚度H和边长D相同,模型见图3.数值模拟中浮冰物理属性根据船模试验中的海冰参数,密度取919 kg/m3,剪切模量取8×108Pa,泊松比取0.25.

图3 浮冰冰块模型示意图
文中计算域为长方体,见图4.长16 m、宽4.5 m、高0.6 m,长度方向为x方向,宽度方向为y方向,高度方向为z方向.本次数值模拟不包含水,但设置一个水平面,以便于观察浮冰块的升沉翻转运动.y方向采用周期性的边界条件,保持计算域中的冰块数量不变.计算网格采用离散元的计算网格,网格大小为0.03 m,时间步长设置5×10-6s,网格数量、冰块数量及模拟总时间设置根据具体的工况为准.
3 计算结果分析
3.1 直航船冰数值模拟现象
图5为0.563 m/s航速,浮冰密集度60%,冰厚0.026 7 m,边长0.2 m参数下的3个时间段的航行运动情况,图6为该工况下的船冰接触现象.由图6可见:在船舶航行的过程中,主要在船体和冰块、冰块和冰块之间发生接触碰撞,碰撞接触的部位主要集中在船艏部和肩部,船体平行中体几乎没有冰块的升沉和翻转,船体后方因船体驶过形成开敞区域.在船冰接触中,冰块主要贴着船体表面在船艏部、肩部进行升沉和翻转运动,然后沿着船体表面向船的两侧滑动,并对周围的冰块产生挤压碰撞.

图5 船体航行运动示意图

图6 船冰接触现象图
3.2 直航航速影响计算结果
对浮冰密集度60%,厚度0.026 7 m,边长0.2 m条件下的不同航速0.188、0.282、0.376、0.470、0.563 m/s的船体冰阻力进行了计算,得到的不同航速船体冰阻力曲线与文献的对比情况,见图7.由图7可知:船体所受冰阻力大小随着航速的增加而增大,随着航速的进一步增加,冰阻力增大的趋势减缓.当船速较低时,冰块几乎不发生升沉翻转现象;随着航速的增加,冰块的升沉翻转现象慢慢发生且程度越来越大;随着航速的继续增加,冰块受到水的曳力影响明显而使冰块远离船体运动,冰块与船体的碰撞频率减小,导致冰阻力增大的趋势减缓.

图7 不同航速船体冰阻力
经无因次化处理后,本次数值模拟情况,与郭春雨等[11]在某拖曳水池中进行的冰区航行船舶非冻结冰模型试验的船体冰阻力在量级上和变化趋势上一致,运用Ls-dyna软件的罚函数算法和流固耦合算法进行的冰区船舶在碎冰中航行的数值模拟结果在量级上和变化趋势一致.
3.3 浮冰密集度影响计算结果
对航速0.563 m/s,厚度0.026 7 m,边长0.2 m条件下的不同密集度40%、50%、60%、70%下的船体冰阻力进行了计算,得到的不同密集度条件下的船体冰阻力曲线图见图8.由图8可知,冰阻力随着密集度的增加而增大,从60%密集度增加到70%密集度时,冰阻力有明显的增长趋势.
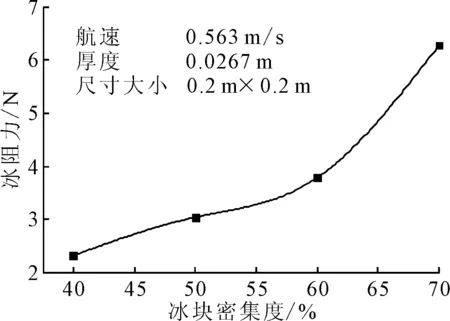
图8 不同密集度下的船体冰阻力
在船舶航行过程中,船艏能够迅速地将冰块冲散到船两侧.在低密集度情况下,冰块有足够的空间散开,冰块的作用范围很小;在高密集度情况下,船艏并不能够迅速地将冰块冲散到船两侧,而是顶着堆积的冰块向前行驶,并在船艏形成堆积现象,见图9,船体与浮冰的碰撞因为密度的增加而加剧,从而导致冰阻力有明显的增长趋势.

图9 70%密集度下的浮冰堆积图
3.4 浮冰厚度及尺寸影响计算结果
对航速0.563 m/s,密集度60%条件下的不同边长0.133 3、0.2、0.266 67 m,和不同冰厚0.016 67、0.026 67、0.04 m下的9种不同参数的船体冰阻力进行了计算.图10为计算得到的船体冰阻力曲线图,在相同的浮冰边长工况下,冰阻力都随着厚度的增加而增大,总体趋势呈线性相关.冰厚的增加使冰块的质量增加,在船与冰接触碰撞后,冰块对船体的冲击动量变大,从而引起冰阻力的增加.

图10 船体冰阻力
在相同的厚度工况下,冰阻力随尺寸的增加而增加,当到达一定尺寸后,冰阻力保持稳定.当冰块尺寸较小时,冰块的作用范围较小,冰块主要受质量影响,尺寸越大,质量越大,冰阻力越大.随着冰块尺寸的增加,冰块的作用范围变大,一方面尺寸的增加会导致冰块的质量的增加,使冰阻力增大;另一方面尺寸会使单位计算区域内的浮冰数量减小,冰块与船体的接触频率减小,使冰阻力减小,最终的结果使船体冰阻力保持稳定.
4 结 论
1)船体冰阻力随航速的增加而增大,随着航速的增加,在航速大于0.470 m/s航速时,冰阻力的增加趋势减缓.
2)随浮冰密集度的增加而增大,在密集度为70%时,冰阻力增长明显.
3)随浮冰厚度的增加而线性增大.
4)随冰块边长的增加而增大,当边长大于0.2 m时,船体冰阻力的无明显变化.
本次计算主要考虑浮冰冰块由多个球形颗粒构成和流体对浮冰的影响两个方面,数值模拟结果通过文献对比,验证了该方法的可行性.但本次计算中浮冰块仍为刚体,未考虑浮冰的破碎现象及浮冰的随机排列,未来的数值研究应在考虑浮冰的破碎现象及浮冰的随机性的基础上进行优化.
