基于粒子法的规则波中浮体运动仿真
2022-03-12宋学敏王绪明刘维勤
宋学敏 王绪明 刘维勤
(高性能舰船技术教育部重点实验室1) 武汉 430063) (武汉理工大学船海与能源动力工程学院2) 武汉 430063)(武汉理工大学国家水运安全工程技术研究中心3) 武汉 430063)
0 引 言
无网格法基本理念是将连续系统以一系列运动粒子来近似,以拉格朗日技术描述空间运动粒子(遵循流体控制方程),以运动粒子表征物理边界且无需网格重构.由此避免了高海况下自由面大变形中网格畸变问题,适用于捕捉强非线性波浪两相流问题(如破波、波浪翻卷等).与网格类方法相比,以拉格朗日法为核心技术的无网格法,计算中无需涉及网格结构,避免了网格生成、网格重构及网格质量所面临的各种问题.
无网格法包括光滑粒子水动力学SPH方法和移动粒子半隐式法MPS方法.目前多数采用显式弱可压缩SPH方法[1-3],包括采用多相流不可压缩ISPH算法[4-6].MPS方法适用于研究自由液面大变形问题如自由液面流体流动问题、破波问题、波浪翻卷.越塚诚一等[7-8]开发了MPS方法并模拟了伴有流体碎片的不可压缩粘性流体流动,柴田和也等[9-11]基于MPS方法研究了甲板上浪冲击的影响,越塚诚一等[12]将MPS方法运用到流固耦合问题的研究中.求解多相流问题的关键技术涉及:交界面粒子的边界捕捉技术;有效实施交界面粒子速度与压力边界条件;局部粒子堆积和分离的移动处理方法;多相压力求解的解耦技术.传统的MPS方法存在搜索粒子耗时、复杂边界处理困难,易产生非物理压力数值振荡(如负压颗粒间空隙、粒子分布不均一),以及自由液面判断准则方式(使某些纯液体粒子误判为自由液面粒子).经过近20年的发展,国内外学者从核函数、压力梯度模型、Laplacian模型、压力Poisson方程中的源项及自由面粒子的判断精度等方面对MPS方法的计算稳定性、精度和效率都进行了系列的改进.Khayyer等[13]对压力梯度的计算进行了改进,提出了一种动量守恒形式(即CMPS),数值结果表明能在一定程度上缓解压力的振荡现象.随后,Khayyer等[14]又提出修改压力Poisson方程源项,提出了高阶源项法(MPS-HS),数值结果表明结合CMPS和MPS-HS方法,即CMPS-HS方法,能够获得较好的效果.万德成等[15-17]基于改进MPS方法、动态负载平衡和MPI(message passing interface)库自主开发了三维并行MPS方法求解器,并进一步将其应用于模拟自由面的流动问题.这些研究工作很大程度地推进了移动粒子半隐式法的发展,但从计算结果上看,这些改进的手段针对不同问题效果不一,还需要更多的应用来验证.有些改进方法实施起来较为繁琐,也需要提出解决问题的新思路.
文中采用改进的MPS方法进行线性波、Stokes二阶波和浮体运动的数值模拟与分析,利用移动粒子半隐式法进行三维的线性波和二阶Stokes波数值波浪水池的研究,基于线性波浪理论生成线性波,并计算结果和理论值分析对比,以及二阶Stokes波的计算和对比验证,验证了MPS方法应用于波浪计算的可行性和可靠性.运用胡克定律模拟浮体的系泊系统,并进行规则波中浮体运动的数值仿真,分析浮式台的运动响应.
1 移动粒子半隐式法
以半隐式算法为核心元素的MPS方法,通过Poisson方程隐式求解压力,确保流体的不可压缩性,显著提升计算稳定性.图1为传统的MPS法流程框架示意图.

图1 传统的MPS法流程框架示意图
1.1 控制方程
在移动粒子半隐式法中,对于不可压缩流体而言,其控制方程是质量和动量守恒方程,为
(1)
(2)
式中:ρ为流体的密度;u为流体的速度;p为压力;μ为运动黏性系数;g为重力加速度.在移动粒子半隐式法中粒子的位置、速度等都是基于拉格朗日描述,粒子法的优势是不用计算对流项.网格法用空间固定计算点来进行计算,速度的拉格朗日微分必须计算式(3)的右边两项,第二项是对流项.
(3)
1.2 粒子相互作用模型
在移动粒子半隐式法中,采用梯度模型和拉普拉斯模型进行控制方程的模拟,为
(4)
(5)
式中:d为空间的维度,二维空间时d=2,三维空间时d=3;n0为标准的粒子数密度;ri为第i个粒子的位置向量;φi为第i个粒子的任意的量;w(r)为由粒子间距离r和影响半径re表示的核函数,此处采用经典的核函数模型考虑粒子间的相互影响见式(6).φi为第i个粒子的最小值,见式(7).
(6)

(7)
φvirtual=0
(8)
在移动粒子半隐式法中,式(5)为由越塚诚一等给出的拉普拉斯模型.其中引入了λ使得数值结果与扩散方程的解析解一致,λ为
(9)
1.3 改进的技术
MPS方法采用了半隐式算法求解N-S方程.N-S方程求解过程中,第一阶段,采用显示解法求解黏性项和重力项;第二阶段,采用隐式解法求解泊松方程.
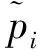
(10)
式中:pvirtual为大气压力.如果pi,pj≥0且pvirtual=0 Pa,式(10)就和式(11)等价
(11)
2 规则波的计算
2.1 流入流出算法
为了生成波浪,在水池的两端使用了流入流出算法作为边界条件,见图2.由图2可知,左右两边的两列假想单元格分别为流入和流出边界.外层的A层假想单元格用作流入单位,粒子会被生成,内侧的B层假想单元格称为辅助单元格用于计算所生成粒子的位置.等边长的立方体表示假想的单元格,立方体的边长等于粒子间的初始距离.流入边界上,如果外侧的A层假想单元格没有粒子,粒子就会被生成在自由液面以下的空的单元格内.新生成的粒子被放在距离邻近外侧假想单元格高度和宽度方向上一定距离的地方.在流动方向的坐标中,这个距离被固定为初始的邻近粒子间距.流出边界上,一旦粒子流出了边界的假想单元格,它们就会被删除.有了流入和流出边界,可以定义任意尺寸的数值波浪水池.

图2 数值波浪水池示意图
在水池中沿着Y轴等间距布置虚拟的圆柱体,测量进入虚拟圆柱体的流体粒子的最大Z轴坐标值,由此,测量得到生成的波浪时程曲线.
2.2 边界上的压力和速度
基于线性波浪理论的理论解析方法,根据伯努利定理的计算值设定边界粒子的压力,可以得到线性波的数值水池计算.同样的,基于二阶Stokes波浪理论的理论解析方法,根据伯努利定理的计算值设定边界粒子的压力,可以在数值水池中生成二阶Stokes波.
方程(12)~(16)表达了二阶Stokes理论.边界流体粒子的X轴和Z轴速度分量由二阶Stokes波浪理论的解析解给出.
(2+cosh 2kh)cos2(kx-ωt)
(12)
(13)
(14)
(15)
ω2=gktanhkh
(16)
2.3 数值水池的验证
将数值水池中计算所得的结果与线性和二阶Stokes波浪理论解析解的结果进行对比分析,从而验证基于移动粒子半隐式法的数值波浪水池的可行性.计算区域的尺寸是6.72 m×0.6 m×1.00 m.验证过程的波浪参数分别为:波长6.72 m、波高0.30 m和波浪周期2.075 s.一阶和二阶Stokes波浪的参数和流体速度的解析解作为初始值和边界值根据波浪理论公式计算得到.在公式的计算中,水深h=8.00 m.实际上,为了节约计算时间,将计算区域可见的水池深度设为1.00 m,然而真实的波浪参数中水深为8.00 m.数值水池底部的粒子的X轴和Z轴的速度根据式(14)~(15)计算得出.
在此验证计算中,流体的密度ρ为1 000 kg/m3.初始的粒子间距为0.03 m.初始时刻的粒子总数为283,552个.进行了20.75 s共计10个波浪周期的波浪传播过程的计算.
2.4 数值结果的分析
通过与二阶Stokes波的理论解进行对比分析,验证了基于移动粒子半隐式法的波浪仿真计算的可行性.图3为一个波浪周期内0.2 s时间间隔波浪粒子图,波浪从右向左传播,整个仿真过程中完整保持了波浪的振幅.图4为MPS方法的线性波的波高时程曲线的计算结果和线性波的理论值的时程曲线的对比.粗曲线代表仿真计算结果,虚线代表线性波浪理论的理论值,由图4可知:MPS方法的计算结果和线性波浪理论的解析值相当接近,仿真值和理论值最大的相差值是0.025 m相当于8.3%的波幅,这是工程应用中能够接受的误差范围.图5为MPS方法的二阶Stokes波的波高时程曲线的计算结果和二阶Stokes波的理论值的时程曲线的对比.同样地,曲线代表仿真计算结果,虚线代表二阶Stokes波浪理论的理论值,仿真值和理论值之间的差值非常小,仿真值和理论值最大的相差值是0.031 7 m相当于10.6%的波幅.通过上述结果的分析发现,移动粒子半隐式法不仅仅可以用于线性波浪的计算,同时也能用于二阶Stokes波的计算.

图3 各时刻波浪速度云图

图4 MPS方法的线性波的仿真结果和理论值的时间曲线

图5 MPS方法的二阶Stokes波的仿真结果波高和理论值的时间曲线
3 系泊的浮体运动仿真
3.1 系泊模型
假设系泊模型由极细的弹性绳索组成,可以忽略绳索与流体之间的相互作用.因此,可以用胡克定律来简化计算系泊模型力.系泊模型的长度可以通过刚体上的固定点与水底的距离来计算.根据实际系泊模型,当长度小于初始长度时,系泊力Fm为零.相反,系泊力Fm为
(17)
根据式(18)~式(19),计算刚体上系泊点a与水底系泊点b之间的不动点长度,(Xa,Ya,Za),(Xb,Yb,Zb)分别为“a”“b”点的x,y,z方向上的位置.系泊模型示意图见图6.初始长度是一个常数L0.
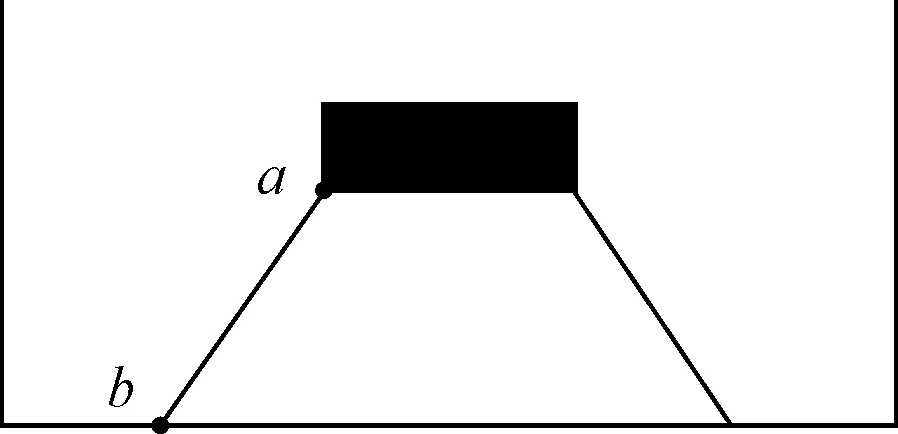
图6 系泊模型
ΔL=L-L0
(18)
(19)
3.2 浮式平台仿真
为了验证本研究中数值方法的可靠性,进行了文献[17]中水池试验工况的数值模拟,具体模型参数、工况波浪参数和文献中一致.运用三维设计软件建立了浮式平台的三维模型,利用三维软件的数据生成等粒子间距的输入文件,粒子间距等于0.01 m.数值模拟中采用与水池试验相同的浮式平台主要特征参数和相同的波浪参数.水池试验情况见图7.

图7 水池试验示意图
根据文献[17]中的试验条件建立了规则波条件下的三维浮式平台模型,并对该模型进行了数值模拟.在数值计算中:①在三维模型中考虑系泊模型;②建立了三维浮式平台模型;③实现了浮式平台6个自由度的运动的计算.通过对浮式平台运动幅值的简单平均得到MPS法的计算结果,表1中比较了浮式平台的纵荡、垂荡、纵摇运动的振幅.结果表明,数值计算结果和试验结果误差在15%以内满足工程应用的要求.

表1 数值计算结果和试验结果对比
4 结 束 语
文中在传统的MPS方法的基础上加入了改进的压力梯度模型,依托该改进的程序分别进行了线性波和二阶Stokes波的数值波浪水池研究和模拟,通过MPS方法的数值计算结果和理论值结果对比分析,发现MPS方法可以生成任意波浪参数的线性波和二阶Stokes波,并且计算结果满足工程应用的精度要求.然后,基于改进的MPS方法的数值造波算法,引入了胡克定律模拟浮体的系泊系统,开展了规则波中浮体运动仿真.本研究一方面验证了MPS方法应用于数值造波计算的有效性和可靠性,为研究航行中船舶砰击、甲板上浪、船舶水弹性等强非线性流体计算提供了可能性.另一方面将该数值方法应用于波浪中系泊浮体运动的模拟,为MPS方法在船舶工程领域更广泛的应用提供新思路.
