基于GPS的常规公交行程时间可靠性因素分析

王 玲 王艳丽 戚新洲 马万经

(同济大学道路与交通工程教育部重点实验室 上海 201804)

0 引 言

在当前积极推进公交优先发展的背景下，如何提升城市公交服务品质提高公交吸引力是当前公交发展的主要任务.而品质和吸引力的提高则需要公交服务可靠性的保障.常规公交仍然是我国大多城市公交系统的主体，相较于蓬勃发展的轨道交通，除了运营速度较慢，关键在于其行程时间的可靠性相对较差.特别是在交通网络较为复杂的大城市，交通拥挤等问题日益严峻，增加了公交车的在途时间，从而影响了公交线路的行程时间可靠性.所以对于常规公交线路的行程时间可靠性进行分析以提高服务可靠性对于提升公交服务品质与吸引力极为重要.

目前，对于常规公交可靠性已经有较多研究，包括路网连通可靠性、服务可靠性以及运行可靠性[1].其中，对于公交运行可靠性的研究，主要集中于可靠性的评价包括评价指标和评价方法、可靠性的影响因素分析以及可靠性的预测模型三个方面.在评价方面，提出了不同的评价指标，如准点率[2]、到达可靠性[3]、行程时间可靠性[4-5]、行车间隔可靠性[6]、候车时间可靠性[7]等，其中，行程时间可靠性是目前公交系统可靠性评价中应用最多，可以综合体现准时、稳定、延误等.对于行程时间可靠性的影响因素，结合不同的案例进行了影响因素分析[8-9]，发现线路长度[10]、道路交通状态[11]、站点数量[12]、站点区间长度[13]等是显著影响因素，而行程时间与影响因素的分析仍以两者的相关分析为主，或者是进行多元线性回归分析.对于行程时间的预测方法上，目前多是针对具体线路构建模型如多元回归模型[14]、神经网络[15]、向量机模型、贝叶斯网络预测、指数平滑技术与基于卡尔曼滤波(KF)的递归方法结合的混合模型等对公交到站时间进行预测.目前综合分析因素对行程时间可靠性的影响较少.总的来说，对于行程时间可靠性的评价指标和计算，大多是针对某一条或者几条线路的评价，影响因素的分析也多是选定一条或几条公交线路，分析的结果也许并不能反映整体状况，有必要研究城市范围内的常规公交线路，给出一般性结论.同时，以往研究多将行程时间可靠性作为连续变量处理，但出行者对公交可靠性的感知，多为分类变量，如可靠与不可靠，故有必要对可靠性进行分类处理，从而得到影响因素与公交线路是否可靠之间的关系.

文中从城市公交线网整体出发，提出评价公交线路行程时间可靠性的指标，并以上海市为例，基于所有的公交线路运行GPS数据，分析影响公交线路行程时间可靠性的显著因素，以及影响规律，并构建逻辑回归模型定量分析影响因素与公交线路可靠性间的关联.

1 行程时间可靠性的评定

1.1 基准时间

对于乘客而言，其认知的基准时间通常是白天平峰的公交的行程时间.因为白天平峰时的交通状况是1 d中相对最为顺畅的时段，其行程时间的差异较少(见图1)，而且白天出行(06:00—18:00)的人数，约占总出行人次的79.9%，故大多出行者对公交行程时间的基准值应多是白天平峰时公交平均行程时间.

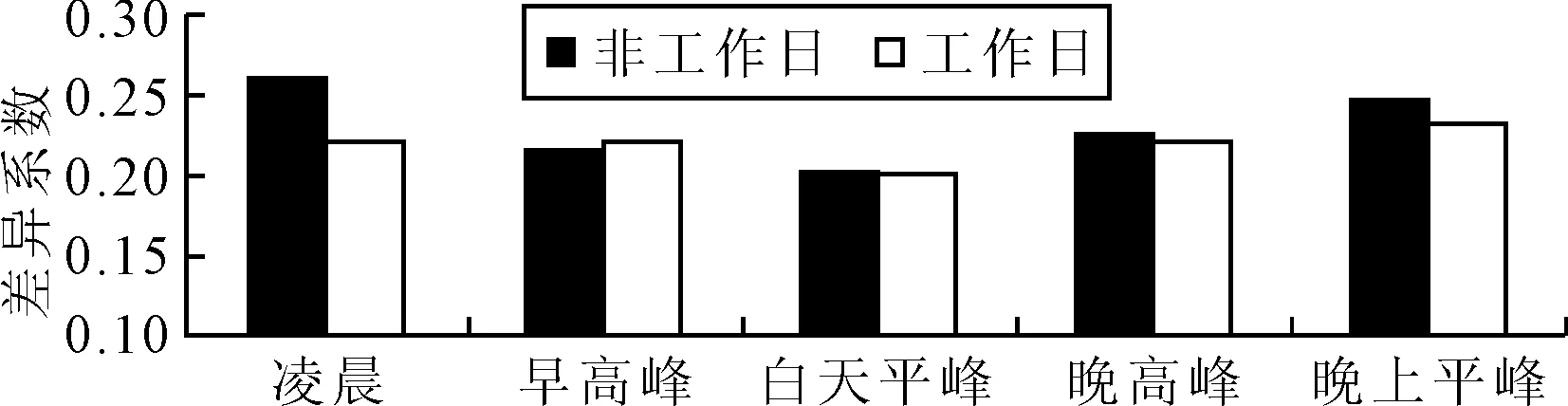
图1 工作日与非工作日各时段行程时间差异系数

1.2 可靠指数

为了评定公交线路与白天平峰时的相近性，提出行程时间可靠指数的概念，即一条线路在某个时间段内从首站到末站(即运行一趟)所耗费时间相对于白天平峰时的相近程度，即

(1)

(2)

(3)

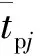
1.3 可靠度

由于出行者对行程时间可靠指数S的具体数值感知并不精确，其对行程时间可靠性的判断通常为可靠或不可靠，所以引入二分变量可靠度R来评定.在用S来表征出行者对某条线路的行程时间与基准值相近性的基础上，将S转换成为二分变量，当S大于等于某个值时，线路运行可靠(R=1)；当S小于某个值时，线路运行不可靠(R=0).

分界阈值的确定取决于城市整体公交线路运行状况，图2为公交行程时间可靠指数分布图.根据上海市的公交运行情况，可靠指数处于70～80范围内时，频次最高；同时，累计频率曲线在70～80区间范围内曲线的切线斜率最大，也就是说，在这个范围内可靠指数变化最显著，因此建议取80作为分界点.

图2 公交行程时间可靠指数分布图

2 可靠性影响因素分析

2.1 数据描述

选取全上海市的常规公交作为研究对象，获取每辆公交在2017年4月1—10日的全部GPS数据.GPS数据的采样间隔为10 s，记录了公交在某时刻(精确到s)的经纬度，同时也记录了车辆的行驶速度，公交在首末公交站点的时间也从GPS数据中获得.共有1 388条线路、826 279条数据样本量.

2.2 变量选取

从线路设置自身初步考虑的变量包括，公交线路的长度、公交线路的站点数量、公交站点的平均间距、公交线路跨越的区域数量、以及公交线路跨越的主要区域类型.其中区域的分类，参照《上海公交线网优化导则》，分为一类区域、二类区域、三类区域.当公交线路跨越几类区域时，频率最高的区域类型作为该线路的主要区域类型；当几种区域类型频率相同时，选择等级更高的区域类型(等级：一类区域>二类区域>三类区域)作为跨越的主要区域类型.

从线路的运行，影响行程时间可靠性造成行程时间波动的因素，主要是受交通状态的影响.交通状态的直接反映指标是速度，所以选取线路平均行程速度作为自变量.

鉴于路网交通流有明显的潮汐性，公交在运行过程中与其他车辆相互影响，所以公交行程时间可靠性也应该分时段分析公交线路行程时间可靠性.根据上海市第五次交通大调查，将一天分为5个研究时段：凌晨0:00—6:00，早高峰6:00—10:00，平峰10:00—15:00，晚高峰15:00—20:00和晚上20:00—24:00.

同时，除了1 d内的交通潮汐情况，工作日与非工作日的交通特性也不尽相同，所以工作日与非工作日也纳入影响因素分析.

对影响因素数据作为变量进行统计，结果见表1.

表1 变量描述性分析

2.3 显著性分析

若影响因素为分类变量则采用卡方检验，否则用T检验，检验结果见表2.

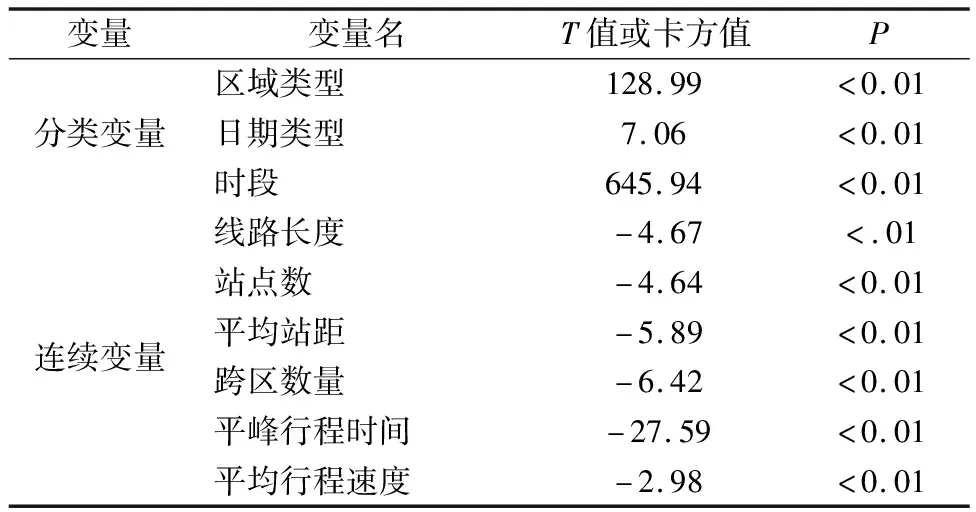
表2 影响因素与公交可靠度R的显著性检验

由表2可知:所有的影响因素变量都与可靠度变量R显著相关.研究进一步分析了影响因素变量间的显著性关系，来排除自变量高度相关，模型变量共线性的问题.结果表明:自变量间的相关性不强.

2.4 影响的二维性及处理

部分影响因素与可靠度R间存在非单调性关系，比如当公交运行的行程时间很短时，公交运行可靠度高，因为被其他车辆或者红绿灯影响公交运行的机会少；当车辆运行的行程时间很长时，公交运行可靠度高，因为行程时间长的公交线路极有可能经过很多长路段，在这些长路段上，公交车可以提高运行速度来弥补在拥堵或交叉口产生的延误.除了公交行程时间，公交站点数量或许也存在类似情况.

为了定量分析这种非单调性关系，以公交行程时间为例，将所有线路的公交行程时间按照数值从小到大依次排列，选取九个等分点，将行程时间数值划分为10个区间，得到在每一个区间的线路可靠度概率(p=可靠度为1的线路数/总线路数)，并计算其发生比的自然对数值，也就是Logit(p)，结果见图3.

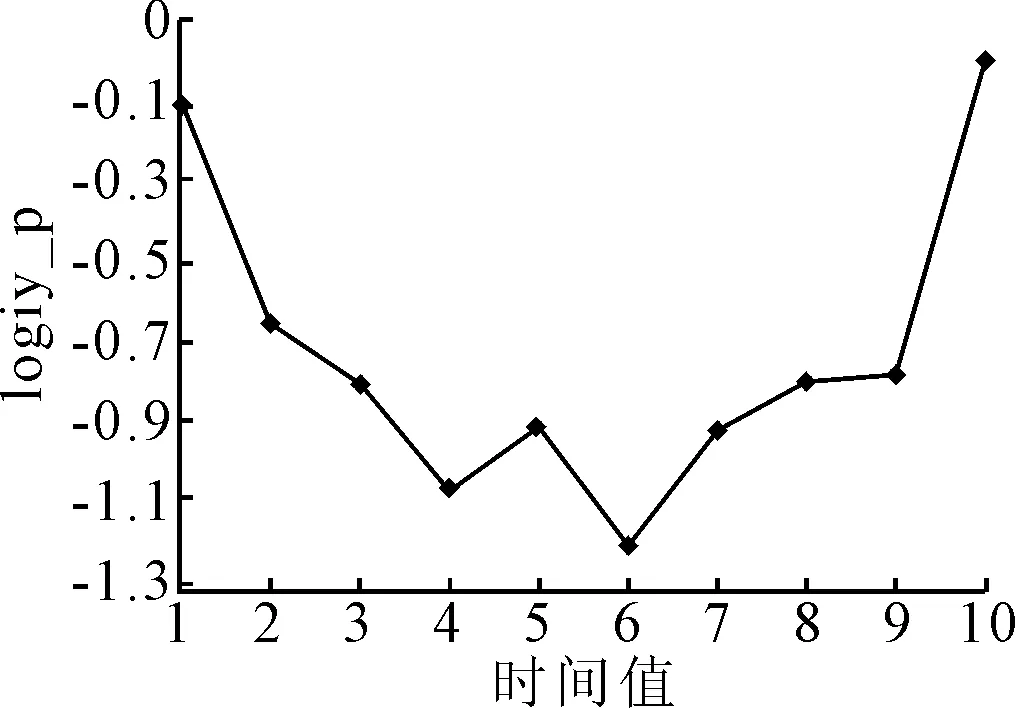
图3 不同行程时间组的Logit(p)

图3表明当公交的行程时间的区间为第6区间时，Logit(p)最低，也就是说行程可靠度最低；而当行程时间离第6区间越远，Logit(p)越高，证明行程时间可靠度越好，第六组的平均值为3 886 s.

公交站点数量也存在和行程时间类似的情况：当公交站点数量处于中间状态(21站)时，行程时间可靠度最好，当公交站点数量与中间状态差距越大，公交的可靠度越差.

若将这两个变量直接放入模型中，这些重要的信息难以得到体现，故需对这两个变量做转换：分别取行程时间与其平均值(3 886 s)和站点数量与其中间状态(21站)差额的绝对值.

3 定量关系分析

3.1 模型的构建

构建贝叶斯逻辑回归模型来定量分析显著影响因素与公交行程时间可靠度R之间的关系.传统的逻辑回归模型认为模型中自变量的系数是一个确定值，但是贝叶斯模型认为自变量的系数服从一个预定的分布，并且贝叶斯模型能以上一次模型的结果作为参考，更新模型，用多次稳定的回归结果来得到自变量系数的分布情况.

行程时间可靠度，可靠与不可靠，发生的比例分别为p(R=1)和1-p(R=0).贝叶斯逻辑回归模型为

(4)

式中：β0距；xj为第j个自变量；βj为第j个自变量的系数.因为没有类似研究能为βj参考，所以采用无信息先验分布，认为β0服从以下分布：

β0～N(0,106)

βj～N(0,106)

行程时间可靠度的贝叶斯逻辑回归模型通过R语言调用Winbugs得到.一共有10 000次模型迭代，其中前5 000次模型迭代没有用于模型结果中，因为初始迭代的结果存在很大的波动性且受初始值影响大，故不能反映真实的自变量系数情况.本研究将后5 000次模型迭代的结果用于得到变量的系数，同时也检查了这5 000次迭代的系数值，结果显示自变量系数的数值稳定，故采用后5 000此迭代的结果是合理的.

3.2 结果解析

研究随机抽取70%的样本作为模型标定的样本，剩余30%作为模型检验的样本.对于标定样本，最先将表2中除了站点数目以及行程时间外的所有变量，以及转换过后的站点数目与行程时间放入贝叶斯逻辑回归模型中，然后将那些在95%贝叶斯区间不显著的变量一一剔除，最终的模型结果见表3.

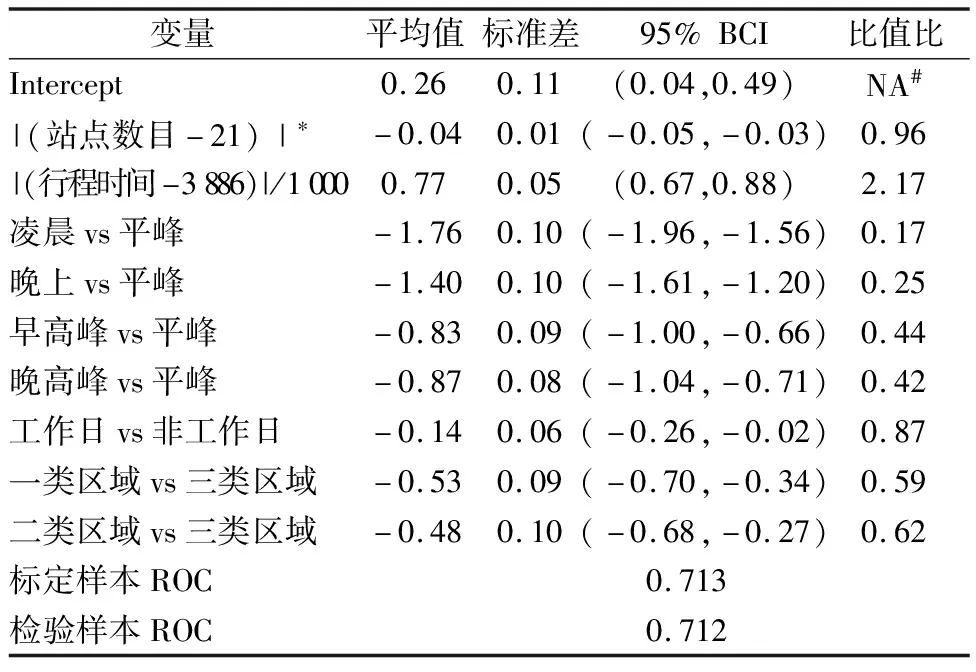
表3 模型结果

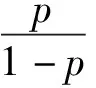
当行程时间与3 886 s相差越大，公交的行程可靠性增加，差距每增加1 000 s，行程时间可靠的发生比增加117%.行程时间很短时，因为被其他车辆或者红绿灯影响公交运行的时间长度短，所以公交运行可靠度高；当车辆运行的行程时间很长时，公交可以在此长时间段，调整速度，以弥补因拥堵或其他突发事件而产生的延误.

相对于平峰而言，凌晨、晚上、早晚高峰的行程时间可靠度较差.工作日相对于非工作日而言，行程时间可靠度较差，这是因为工作日与非工作日相比，出行车辆更多，公交受其他车辆的影响更大.

相对于第三类区域而言，第一类与第二类区域的行程时间可靠度较差.第一类区域为内环内，第二类区域为内外环之间或郊区新城及重点开发，第三类区域为外环外的其他地区，故相对于第三类区域而言，第一类与第二类区域的交通更为拥堵，所以行程可靠度更低.

4 结 束 语

文中提出了可靠度指数和运行可靠度作为整条线路的行程时间可靠性的评价指标，运用上海市公交线路的运行数据进行分析，发现线路平均行程速度、公交线路跨越的区域数量、公交线路的长度、公交线路的站点数量、公交站点的平均间距、公交线路跨越的主要区域类型、以及运行时段、工作日与非工作日都会影响其可靠性，并建立了贝叶斯逻辑回归模型来反映其定量关系.但研究由于数据限制，只分析了的线路的起点到终点的行程时间可靠性，后续可以细化研究站点到站点间的行程时间可靠度.同时，鉴于天气对公交运行也有影响，后需将融合交通气象数据，将天气纳入对公交行程时间可靠度的影响分析中.