Cu-Ni-Ti 合金高温热变形行为及热加工图

2022-03-12李律达洪鑫满绪存陈俏张建波刘锦平

有色金属科学与工程 2022年1期

李律达，洪鑫，满绪存，陈俏，张建波*，刘锦平

（江西理工大学，a. 材料冶金化学学部； b. 应用科学学院，江西赣州 341000）

0 引言

铜合金系列具有良好的导电、导热性能，被广泛应用于电子信息[1-2]、轨道交通[3-4]、机械制造[5-6]等领域。随着大规模集成电路和高速电车轨道系统的快速发展，对其综合性能提出更高需求，众多企业和研究机构开发出Cu-Ni-Si、Cu-Ni-Sn、Cu-Ni-Ti 等时效强化型铜合金。目前，Cu-Ni-Si、Cu-Ni-Sn 的应用较成熟，Cu-Ni-Ti 合金的文献报道主要集中于相图计算[7-8]、组织和性能[9-10]、析出相[11]。当Ni、Ti 质量比接近7 时，经950 ℃、固溶处理1 h 和600 ℃、1 h 时效处理后，析出相Ni3Ti 具有明显的沉淀强化作用，能够获得抗拉强度为600 MPa，导电率为60% IACS，伸长率为10%，高温软化温度为650 ℃的Cu-0.58Ni-2.06Ti 合金。Cu-Ni 系列的高温热变形行为有大量报道[12-14]，但关于Cu-Ni-Ti 合金系列热加工性能的文献报道较少，已有研究多为工艺研究[15]，其高温热变形行为研究仍处于空白。对于铜合金而言，热加工是提高其性能的重要手段，优化热工艺参数能有效调控合金的组织与性能。为了探究最优工艺，研究者建立了基于动态材料模型（DMM 模型）的热加工图，并且成功应用于多种钢[16]、铁基合金[17]、铝合金和铜合金[18-19]等材料。 DMM 模型是通过热变形试验研究应变、应变速率和温度之间的关系，也是描述高温下合金的流变应力、应变速率和温度之间关系的综合模型，根据此模型绘制合金的热加工图，从而确定最佳工艺。综上，对Cu-Ni-Ti 合金应用动态本构模型和热加工图，将成为其热变形工艺优化的重要理论依据。

本研究采用MMS-100 热力模拟机对Cu-Ni-Ti合金在不同温度和不同应变速率条件下开展热压缩试验，研究了合金在热变形过程中的流变应力与应变温度、应变速率之间的关系，建立了描述Cu-Ni-Ti 合金高温流动应力、应变率和温度关系的本构模型和热加工图，并对本构方程的有效性进行了研究，分析了不同应变、应变温度和应变速率下的金相组织。

1 材料制备与方法

实验采用纯度为99.9%的电解铜、99.9%Ni、Cu-10Cr 中间合金、Cu-50Ti 中间合金，通过真空中频感应电磁炉经熔炼浇注获得Cu-Ni-Ti 棒材，浇注温度为1 100～1 200 ℃，其化学成分如表1 所列。为了消除熔铸过程中产生的枝晶偏析，对铸态合金进行温度为800 ℃，时间为20 h 的均匀化热处理，最后随炉冷却。加工直径为10 mm，高度为15 mm 的圆柱形压缩试样。在MMS-100 热力模拟机进行等温压缩实验，变形温度为700、750、800、850 ℃。应变速率为0.1、1、5、10 s-1，总变形量为0.6。热模拟升温速率为10 ℃/s，加热到达预定温度后，保温3 min，完成等温压缩试验后水淬。

表1 Cu-Ni-Ti 合金化学成分Table 1 Chemical composition of Cu-Ni-Ti alloy单位：质量分数，%

2 结果与讨论

2.1 真应力-应变曲线

图1 所示为Cu-Ni-Ti 合金不同变形条件下的应力-应变曲线，由图1 可知，应力-应变曲线在不同应变温度和应变速率的条件下，其变化规律基本相近。随应变程度增加，流变应力快速上升至极限值后逐渐转变为平缓曲线，在等温压缩初期，变形程度较小，均匀化合金等轴晶较多，变形增加使材料中的位错攀移、滑移、增殖互相发生交互作用，出现加工硬化现象，其应力快速上升。随后，当变形温度超过一定临界值时，提供了回复再结晶所需的能量，变形基体位错密度减小并重新产生新的等轴晶使合金软化，加工硬化与动态回复再结晶彼此达到平衡[20]，故应力曲线趋于平缓。图1（b）中850 ℃应力-应变曲线有明显的屈服现象，这是因为屈服前，溶质原子偏聚在位错及其他缺陷周围，对位错、晶界的迁移起钉扎作用，随着温度与外力作用增加，位错挣脱束缚并不再需要更大的应力，流变应力趋于平缓。

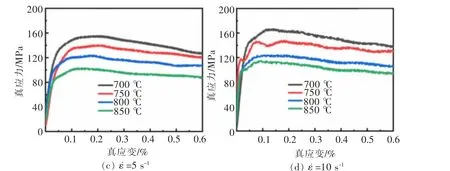
图1 Cu-Ni-Ti 合金不同变形条件下的应力-应变曲线Fig. 1 Stress-strain curves of Cu-Ni-Ti alloy under different deformation conditions

图2 所示为Cu-Ni-Ti 合金在不同变形温度和速率下的峰值应力，综合图1 和图2 可知，在变形温度相同条件下，随应变速率增加，加工硬化效果增强，峰值应力上升；在变形速率相同条件下，随变形温度增加，峰值应力下降[21]。图2 中，在700 ℃，应变速率由0.1 s-1增加至10 s-1时，峰值应力由116.8 MPa 增加至160.9 MPa，增加了37%；在850 ℃，应变速率由0.1 s-1增加至10 s-1时，峰值应力由66.5 MPa 增加至113.1 MPa，增加了70%。在0.1 s-1，变形温度由700 ℃增加至850 ℃时，峰值应力由116.8 MPa 下降至66.5 MPa，下降了43%；应变速率为10 s-1，变形温度由700 ℃增加至850℃时，峰值应力由160.9 MPa下降至113.1 MPa，下降了30%。由此可见，应变速率对峰值应力的影响更大。

图2 Cu-Ni-Ti 合金不同变形温度和速率下的峰值应力Fig. 2 Peak stress of Cu-Ni-Ti alloy at different strain temperatures and rates

2.2 本构方程的建立

根据图1 和图2 可知，Cu-Ni-Ti 合金的变形温度和峰值应力与应变速率之间存在一定的相关性，采用Sellars 和MCTegart 提出的双曲正弦修正的Arrhenius 型方程[22]描述三者之间的关系，如式（1）所示：

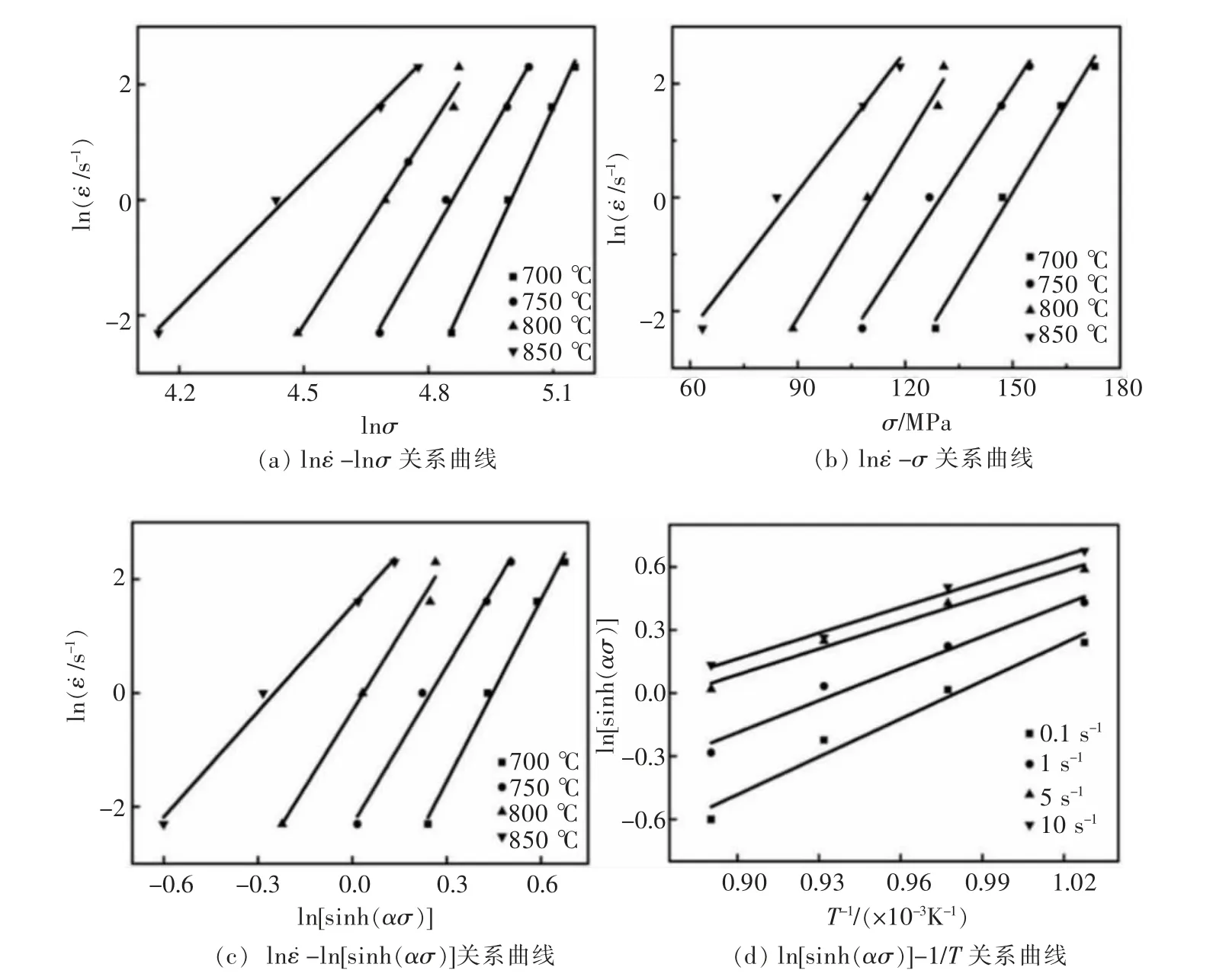
图3 应力与应变速率和温度之间关系曲线Fig. 3 Curves of the relationship between stress and strain rate and temperature

在应变为0.2～1.0 的范围内，以相同的方法求解不同应变的α、n、Q 和A 值。对上述变量进行五次多项式拟合，图5 所示为α、n、Q 和A 与真应变关系曲线。以应变ε 为自变量的多项式表达式如下：

图4 lnZ-ln[sinh（ασ）]关系曲线Fig. 4 lnZ-ln[sinh（ασ）]relation curve

图5 α、n、Q 和A 与真应变关系曲线Fig. 5 The relationship between α，n，Q and A and true strain

表2 α、n、Q 和A 多项式系数Table 2 Coefficients of α，n，Q and A polynomials

图6 所示为ε=0.2 时，应力计算值与实际值的误差曲线，通过线性拟合后可得：应力计算值与实际值的误差曲线相关系数R2=0.990 6，说明上述本构方程准确性较高。

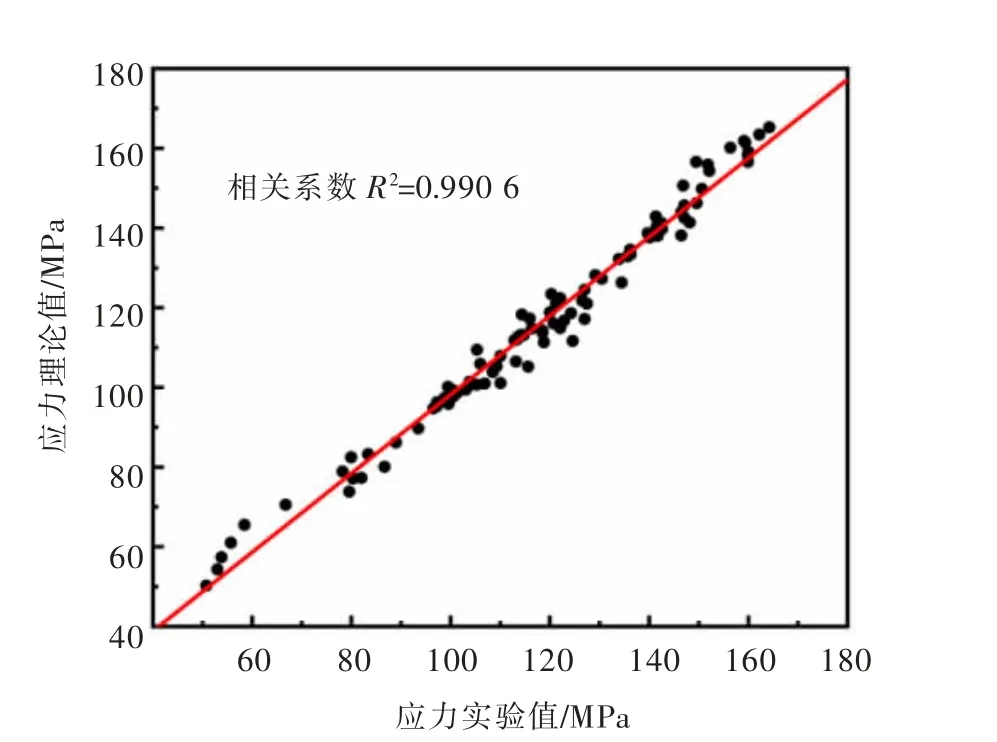
图6 计算值与实际值的误差曲线Fig. 6 Error curve between calculated and actual values

2.3 热加工图

根据塑性变形力学和热力学原理[24]可知，合金热变形时，外界对材料做的总功将以2 种形式耗散，第1 种为塑性变形，其中大部分转化为热能，少部分储存于晶体缺陷中；第2 种为组织演变。用于塑性变形的能量称作耗散量以G 表示，而消耗于组织演变的能量称为耗散协量以J 表示，总输入能量由P 表示。通过应力σ 和变形速率ε·表示三者之间关系，具体如式（11）、式（12）、式（13）所示：

式（17）中，ξ 为失稳因子，ξ＜0 表示材料处于塑性失稳态，区域内会产生开裂、绝热剪切带等缺陷。

实际热变形时，从本构方程可知，σ 与ε·之间的关系并不是简单的幂函数，此时式（16）和式（17）不适用于本构方程模型。因此，直接将式（9）代入式（12）由定积分计算得出J，依据定义得Jmax=ε·σ/2。

失稳因子ξ=2m-η，利用能量耗散因子η 和失稳因子ξ 绘制热加工图。将应变量为0.4 和0.6 的功率耗散图和失稳图叠加得到热加工图，如图7 所示，图7 中等值线表示能量耗散因子η 值，阴影部分代表失稳区。图7（a）显示了Cu-Ni-Ti 合金在应变量为0.4 时的热加工图，随温度增加，耗散因子η 值逐渐增大，在840～850 ℃区间内η 达到峰值为0.30；随应变速率增加，耗散因子η 值逐渐减小。图7（a）存在温度为700～725 ℃和775～830 ℃，应变速率为1～10 s-1的2 个失稳区，区域内最低耗散因子η 分别为0.093和0.063。 Cu-Ni-Ti 合金在高变形速率下位错、缺陷和畸变基体之间产生强烈的交互作用，位错增殖、塞积和缠结程度剧烈增加，加工硬化强于动态回复、再结晶导致材料出现失稳。图7（b）是Cu-Ni-Ti 合金在应变量为0.6 时的热加工图，耗散因子η 随温度和应变速率变化趋势与图7（a）基本一致，其失稳区在温度为700～820 ℃，应变速率为1～10 s-1的范围内，其大部分范围为中低温高应变速率区域，其中最低耗散因子η 为0.053 和0.035，由于变形程度增加，加工硬化效果更强烈，在低耗散区能量更容易集中，产生晶格畸变和晶界裂纹，从而产生失稳。对比图7（a）与图7（b）可看出，随应变量增加，能量耗散效率整体明显降低，失稳区域增大。综合可得，Cu-Ni-Ti 合金较优工艺的温度为840～850 ℃，应变速率为0.1～1 s-1区间内。

图7 Cu-Ni-Ti 合金在不同应变下的热加工曲线Fig. 7 Hot processing map of Cu-Ni-Ti alloy under different strains

为了进一步阐明Cu-Ni-Ti 合金在不同应变下失稳区产生的原因，对ε=0.6 的合金进行了金相组织分析。图8 所示为不同变形条件下Cu-Ni-Ti 合金的显微组织。图8（a）显示了均匀化态的Cu-Ni-Ti 合金，其组织分布均匀，为条状枝晶。图8（b）和图8（c）分别为700 ℃、10 s-1和750℃、10 s-1条件下的金相组织图，具有明显的绝热剪切带组织特征，热加工图显示其为失稳区，晶粒在外部压力作用下，呈长条状，未发现等轴晶粒。由图8（d）和8（e）可知，当温度进一步增加达到800 ℃和850 ℃时，大部分变形组织经动态回复再结晶转变为等轴晶，未发现明显的纤维组织。根据热加工图可知，温度越高，合金耗散量更大，有利于纤维组织转变为等轴晶，耗散因子峰值出现在850 ℃。