圆柱壳结构的转角自由度频响函数估计方法研究1)
2022-03-12李旭龙董俊辉陈立群
李旭龙 张 忠 董俊辉 魏 莎,, 陈立群,
∗(上海大学力学与工程科学学院,上海 200444)
†(北京强度环境研究所可靠性与环境工程技术重点实验室,北京 100076)
∗∗(哈尔滨工业大学(深圳) 理学院,深圳 518055)††(上海市应用数学和力学研究所,上海 200072)
近年来,随着航空航天、船舶和机械等工程领域的迅速发展,越来越多的复杂结构被运用于工程实际,这对其结构动态分析结果的准确性提出了更高的要求。目前,针对大型复杂结构展开有限元仿真计算,需要耗费大量的计算成本,不利于复杂结构中部件的优化设计,频响函数子结构方法为该问题提供了解决思路。该方法将复杂结构进行子结构划分,并对每个子结构进行动态特性分析,最后根据位移协调条件和界面力平衡条件求得整体结构的动态特性[1-2]。同时,相较于模态综合方法,其无需考虑剩余模态和主模态个数的限制,适用于模态密集和较大阻尼结构。但该方法同样须克服诸多难题,在实验测试过程中由于无法进行纯弯矩激励且一般传感器无法对转角自由度数据进行测量,因此转角自由度信息的获取成为了难题之一。
许多学者针对实验测试中存在的转角自由度信息缺失问题展开了相关研究。Liu 等[3]详细讨论了转角自由度信息在频响函数子结构综合方法中的重要性,并指出不考虑该信息进行综合会导致错误的综合结果。Duarte 等[4]采用有限差分法获取了与转角自由度相关的频响函数,具有较高的计算精度,但该方法对试验件的结构有较高要求。Avitabile 等[5]采用测试得到的平动自由度信息进行模态参数识别,并将计算得到的模态振型和残余模态进行扩展从而得到相应的转角自由度频响函数。de Klerk 等[6]提出界面刚性等效方法,假设连接点处的多个拾振点位于同一刚体区域内,通过耦合多个拾振点的平动自由度信息计算得到连接点的转角自由度信息,避免了转角自由度的直接测量。
本文介绍了界面刚性等效方法的基本理论,并将该方法用于圆柱壳结构的转角自由度信息缺失问题。通过对圆柱壳结构的数值仿真和实验研究,验证了该方法的可行性。此外,结果表明该方法的计算结果具有较高的精度,可用于频响函数子结构综合方法的研究。
1 界面刚性等效方法
1.1 基本理论
界面刚性等效(equivalent multi-point connection, EMPC) 方法[6-8]将子结构连接界面视为刚性面,按刚体运动理论对界面进行刚性等效。通过耦合连接点附近的多个平动自由度信息,进行子结构连接点转角自由度信息的近似估计。以对接圆柱壳结构为例,可根据连接特性将其分为子结构A 和B。由系统输入、输出关系,可得到子结构的频率响应方程为[9-10]

为简要说明界面刚性等效方法中变换矩阵R的构成,以每个连接点附近布置三个三轴加速度传感器的典型配置为例,如图1 所示。该结构由子结构A 和B 组成,连接界面为1~3 号节点组成的平面,两子结构在界面处完全固结。将1~3 号节点的拾振点通过符号k(k= 1,2,3) 表示,每个拾振点仅包含3 个平动自由度。

图1 对接结构示意图Fig.1 Schematic diagram of docking structure
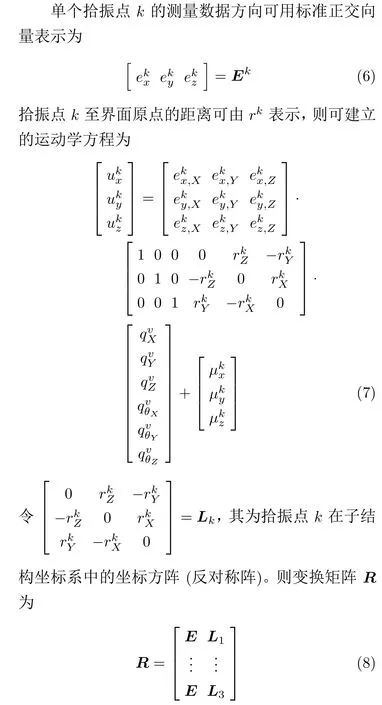
其中,E为单位矩阵。
1.2 界面刚性指数
基于上述理论,可通过连接点附近多个拾振点所组成的局部变形模态对界面连接点转角自由度信息进行近似估计。如果拾振点选取不当将直接导致估计精度的降低。de Klerk 定义的界面刚性指数可作为拾振点选取优劣的评判依据[6,11]。通过子结构连接界面的原自由度响应与转换得到的等效自由度响应的比值,判断局部变形模态是否能够较好地描述界面连接点。不考虑内部点自由度响应,由式(3)可得
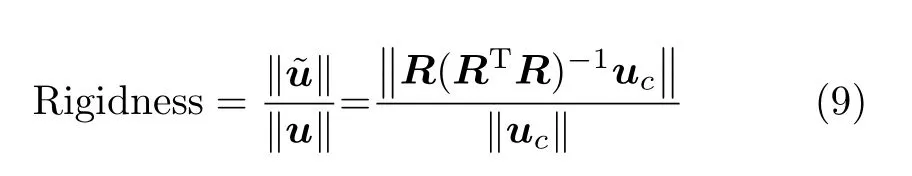
当界面完全刚性时,根据刚体运动特点可知剩余自由度响应µ趋近于零。此时,界面等效自由度响应˜u趋近于原自由度响应u,则界面刚性指数接近“1”,也就是说界面连接点可以被较好地描述,反之则描述效果较差。同样以图1 所示结构为例说明界面刚性指数的计算过程。
令内部节点力fi=0,可得

其中,下标1~3 为拾振点编号。
将式(8)、式(3) 代入式(1) 便可得到子结构连接界面刚性指数。
2 圆柱壳结构数值仿真研究
2.1 仿真模型
将界面刚性等效方法应用于对接圆柱壳结构。仿真过程中采用ABAQUS 有限元分析软件对圆柱壳结构进行频响函数的计算,以下称作“有限元频响”。同时,为模拟实验条件下界面转角自由度信息不可测的情况,采用EMPC 方法耦合多个拾振点的平动自由度信息以进行界面连接点转角自由度信息的近似估计,以下称作 “EMPC 计算频响”。图2 为圆柱壳结构的连接界面示意图,其中1~3号点为待耦合的拾振点,4 号点为待估计的界面连接点。

图2 圆柱壳结构连接界面示意图Fig.2 Schematic diagram of the connection interface of cylindrical shell structure
由于EMPC 理论基于界面刚性假设,故选取三个较为靠近界面连接点的位置作为拾振点。以法兰盘为坐标原点,则三点坐标分别为:1(163.3, 13.2,0),2(185, 0, 0),3(163.3,-13.2, 0),通过式(8) 便可组成变换矩阵R。
2.2 仿真结果及分析
通过EMPC 方法耦合1~3 号点的线自由度信息,可对4 号连接点进行转角自由度信息的近似估计。同时,将EMPC 计算频响与有限元频响进行对比,如表1 所示为二者的峰值误差与峰值处频率误差汇总。
从表1 所得的相对误差可以看出,EMPC 计算频响与有限元频响吻合较好,其最大峰值误差为2.67 dB,峰值处的频率误差为0 Hz,均在误差允许范围内。结果表明界面刚性等效方法可以近似估计圆柱壳结构界面连接点的转角自由度信息。
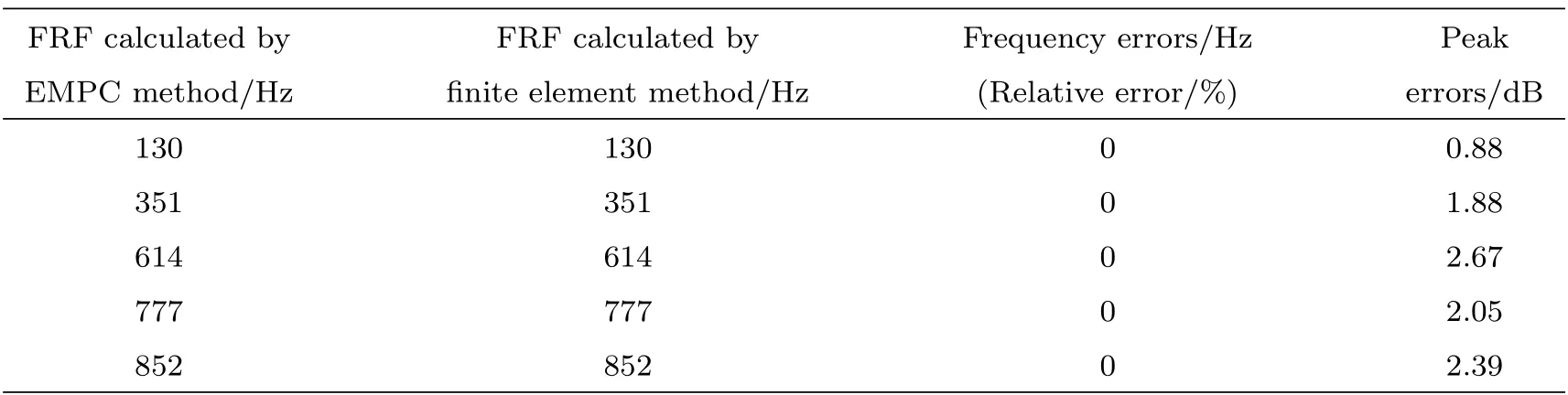
表1 EMPC 计算频响与有限元频响结果的频率误差和峰值误差汇总表Table 1 Summary of frequency errors and peak errors of FRF calculated by EMPC method and finite element method
3 圆柱壳结构试验研究
3.1 实验模型及测试方案
为进一步验证界面刚性等效方法的正确性及其在对接结构中的有效性,采用上述方法对图3 所示的圆柱壳结构进行界面转角自由度信息的近似估计,其中1~4 号点为界面连接点。圆柱壳结构的基本参数信息为:筒壁内径D1= 292 mm,筒壁外径D2= 300 mm,筒壁长度L= 500 mm,法兰厚度b=30 mm,法兰外伸长度h=35 mm。

图3 圆柱壳结构示意图Fig.3 Schematic diagram of cylindrical shell structure
3.2 实验结果及分析
为正确评估EMPC 计算频响的正确性,需结合圆柱壳结构模态振动特性,故本节开展了该结构的实验模态测试与分析[12]。实验过程中通过弹性绳进行圆柱壳结构自由边界的实验实现,采用单点激励多点响应形式,利用冲击力锤施加脉冲激励,力传感器信号和拾振点处的三轴加速度传感器信号反馈给数据采集系统。数据采集系统结合输入和输出信号进行曲线拟合,从而识别系统模态参数,试验模态测试系统如图4 所示。

图4 实验模态测试系统示意图Fig.4 Schematic diagram of experimental modal test system
依次对112 个测点进行径向激励并对对应的频响函数进行5 次有效值平均,计算得到前6 阶固有频率及阻尼比,如表2 所示,其中m和n分别表示轴向波数与周向半波数。

表2 圆柱壳结构前6 阶模态参数Table 2 The first six modal parameters of cylindrical shell structure
由表2 可以发现,带有法兰的圆柱壳结构仍然保留了薄壳振动的大多数特点:(1) 呼吸振型,其轴向和周向都呈现出周期波的特点;(2)其周向的半波数和轴向波数随着模态阶数的增加而呈增加趋势,第3 阶、第5 阶模态虽出现了周向半波数减少的情况,但总体上看其仍满足上述规律,表现为圆柱壳结构的一般振动特性。
基于上述对圆柱壳结构模态参数的求解,现对1~4 号连接点采用图2 所示的拾振点布置,布置结果如图5 所示。同时,为验证拾振点布置的合理性,可根据Klerk 定义的界面刚性指数进行计算[6,11],计算结果如图6 所示。
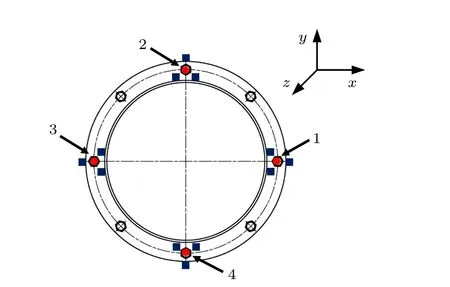
图5 拾振点布置示意图Fig.5 Schematic diagram of pick-up point layout
通过图6 结果可以看出:(1)整个界面的刚性指数随着频率的增加而有所降低,说明拾振点布置是合理的;(2) 250~400 Hz,500~700 Hz 频段处的界面刚性指数较小,界面连接点可能无法得到较好的描述,导致上述频段的频响综合结果较差。上述结论验证了其布置的合理性,由于该过程所用的数据均为实验实测获得,故仍需进行计算精度验证。

图6 界面刚性指数计算结果(Klerk 方法)Fig.6 Calculation result of interface rigidness (Klerk method)
进一步对上述连接点转角自由度信息进行EMPC 方法的近似估计。为便于叙述,将基于实验频响函数EMPC 计算得到的连接点频响函数称为“EMPC 计算频响”。表3 为1 号连接点EMPC 计算频响与有限元频响的频率误差和峰值误差汇总表。由于500~700 Hz 频段界面刚性指数较差,故不对该频段进行讨论。
通过表3 结果可以看出,EMPC 计算频响在各阶固有频率处均有峰值存在。将其与有限元频响进行对比可以发现,二者的频率误差最大为6 Hz(1.68%)、峰值误差最大为1.29 dB,二者具有较高的一致性。因此可得结论:(1)EMPC 方法同样适用于圆柱壳结构;(2) 将实验频响函数进行EMPC 计算得到转角自由度信息具有较高的计算精度,可用于子结构混合建模的研究。

表3 EMPC 计算频响与有限元频响的频率误差和峰值误差汇总表Table 3 Summary of frequency error and peak error of FRF calculated by EMPC method and finite element method
4 结论
本文介绍了界面刚性等效方法,并将其运用于圆柱壳结构的转角自由度信息估计问题。为验证界面刚性等效方法的可行性与计算精度,对圆柱壳结构进行了数值仿真和实验研究,基于上述结果可得结论:(1)界面刚性等效方法可以近似估计连接点的转角自由度信息且可用于圆柱壳结构;(2)圆柱壳结构连接点经过界面刚性等效方法计算后,其结果与有限元结果相吻合,具有较高的计算精度;(3) 经界面刚性等效方法计算得到的转角自由度信息可用于子结构混合建模研究,以提高混合建模精度。
