基于顶点线性插值的建筑物群聚合的简易方法

黄玉兰，郭庆胜＊,王慧慧,王 勇

（1.武汉大学资源与环境科学学院，湖北 武汉 430079 2.中国测绘科学研究院，北京 100830）

建筑物群作为城市地图中的核心要素，对地图表达的效果具有重要影响[1]。建筑物群的自动聚合是制图综合的难点之一，国内外诸多学者对建筑物群聚合方法进行了大量研究[2-26]。基于相关研究，本文提出了基于顶点线性插值的建筑物群聚合的简易方法：首先利用最短邻近连线获取建筑群邻近关系，然后通过对这些连线的分析、量测和计算准确获取相邻建筑物的聚合部分，最后采用渐进式方法实现建筑物群聚合。该方法还能处理建筑物群的多边形存在相交和重叠空间拓扑关系的聚合问题。此外，本文利用道路网将建筑物群划分到不同区域后进行聚合，既维持了建筑物的空间分布特征，又能提高算法效率。

1 建筑物群的空间邻近关系

空间邻近关系是寻找邻近建筑物进行聚合的重要依据，获取的邻近关系不同，则对应的聚合结果也会有所不同。根据建筑物轮廓线可以构建约束性Delaunay三角网（contrained delaunay triangulation,CDT），然后获取建筑物群的空间邻近关系，但该方法会疏漏一些建筑物之间的空间邻近关系。例如，针对图1a中的建筑物群建立CDT并得到相应的空间邻近图，如图1b所示，此时未探测到建筑物B1与B2及B1与B3之间的空间邻近关系。对此已有学者进行了研究，如文献[23]综合考虑多个影响建筑物群聚的因子，可获取B1与B2及B1与B3之间的空间邻近关系，但未讨论如何量测和计算B1与B2及B1与B3之间的具体相邻情况。

加密插值建筑物轮廓线上的顶点后，构建的建筑物间的CDT和建筑物群的空间邻近图分别如图2a和图2b所示。对比图1和图2可知，等间距加密建筑物轮廓线顶点后，能更准确地探测到建筑物B1与B2及B1与B3之间的空间邻近关系，且相邻建筑物间的空间可由三角形填充。

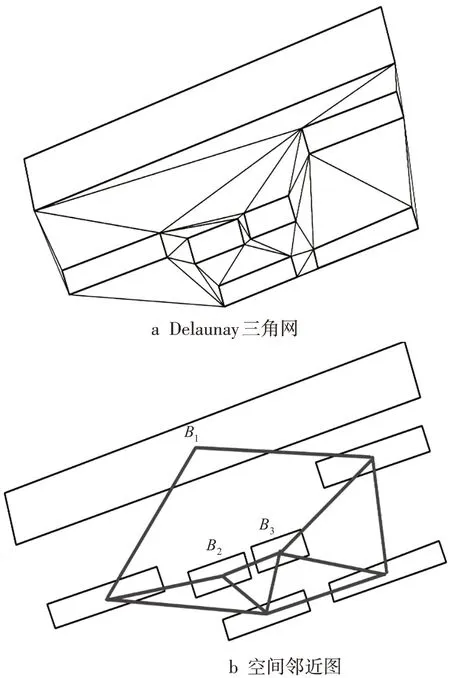
图1 基于CDT的空间邻近关系

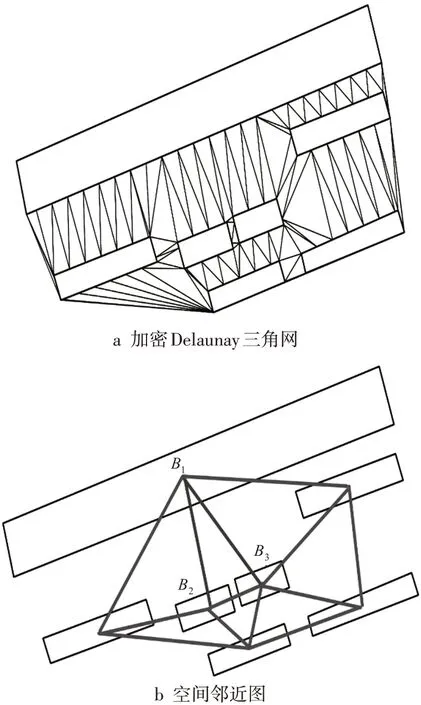
图2 加密顶点后的空间邻近关系

2 搜寻最短邻近连线

建筑物轮廓线顶点加密后，相邻2个建筑物的聚合就有一个直观的理解：相邻建筑物的聚合部分就应该是长度小于阈值的最短距离顶点连线的组合。因此，从一个建筑物轮廓线上的一个顶点到相邻的另一个建筑物轮廓线上最邻近的点之间的连线就非常重要，这里称之为“最短邻近连线”。设a是建筑物A的一个顶点，b是建筑物B的一个顶点，A与B之间是邻近关系，若从a到建筑物B的某个顶点之间距离最小时，建筑物B的这个顶点是b，那么从a到b的连线就是“建筑物A的顶点a到建筑物B的最短邻近连线”。最短邻近连线具有以下特性：

1）dist(a,b)＜dist(a,c),a∈A,b∈B,c∈B,b≠c

2）line(a,b)∩A=Ø

3）line(a,b)∩B=Ø

式中，c表示建筑物B上除b之外的任意顶点；dist表示2个顶点之间的距离；line表示2个顶点之间的连线（不包括a和b）。

基于最短邻近连线的特性就可以构建最短邻近连线网，利用长度小于阈值的最短邻近连线的组合就能确定相邻建筑物的聚合部分。

2.1 数据预处理

数据预处理包括插入交点和通过插值加密建筑物轮廓线顶点2部分。由于数据误差，建筑物之间有可能相交，在这些交点处存在长度为零的特殊最短邻近连线，所以构建最短邻近连线前需插入交点。在建筑物群聚合时，长度小于阈值的最短邻近连线就表示了建筑物群的聚合之处。因此，为了提高建筑物群聚合效果，必须对建筑物轮廓线的顶点加密。处理后的建筑物轮廓点序号在外环中按顺时针方向组织，内环中按逆时针方向组织。

2.2 过滤条件

最短邻近连线网可以准确描述建筑物群的邻近关系，且容易进行长度、角度等几何计算。本文在建立建筑物的一个轮廓点与其所有邻近点之间的邻近连线后，使用位置、属性、长度和角度4个特征度量进行条件过滤，排除不满足聚合要求的连线。具体判断条件如下：

1）属性的过滤条件。邻近连线的端点至少关联一个建筑物。依据端点关联的建筑物ID，可以获取连接相邻的2个建筑物的连线。

2）位置的过滤条件。相离建筑物间的邻近连线不应穿过任何建筑物，而相交建筑物重叠区域的邻近连线应在2个建筑物内部。利用邻近连线的中点M，就可以判断邻近连线的位置。设S1和S2分别为2个建筑物的内部区域，邻近连线能保留下来的条件为：

3）角度的过滤条件。2个视觉邻近的建筑物的待聚合轮廓线应尽量平行，要求最短邻近连线关联的2条轮廓线的方位差小于设定的阈值（设为α）；聚合后的建筑物多边形不应该出现“尖锐角现象”，要求最短邻近连线与关联的每条轮廓边之间的夹角大于设定的阈值（设为δ）。设line(Qi,Pj)为邻近连线，Qi与Pj为轮廓线上点，如图3所示，line(Qi,Pj)连接的待聚合边为e1与e2，则邻近连线能保留下来的条件为：

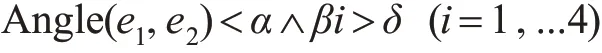
图3 最短邻近连线

4）长度的过滤条件。经上述过滤后保留的邻近连线中长度最短的即可作为当前建筑物轮廓点的最短邻近连线，长度小于聚合距离阈值的最短邻近连线即可用于后续建筑物群的聚合。此外，为了处理建筑物之间相交情况，本文定义建筑物相交区域内部的最短邻近连线的“长度为负值”。

3 构建聚合通道

相邻的2个建筑物聚合时可能会出现在建筑物不同部位进行聚合的情况，这些部位本文称之为“聚合通道”，每个“聚合通道”由一组最短邻近连线组成，“聚合通道”的构建就是搜寻到独立成组的最短邻近连线集合。

设2个邻近建筑物（B1和B2）之间的最短邻近连线集合已经找到，若多条最短邻近连线关联的建筑物轮廓线顶点序号是连续且有序的，那么这个由多条最短邻近连线就组成了一个“聚合通道”；否则，需分2种情况处理：

1）如图4所示，建筑物B1上点Qx与Qk之间所有最短邻近连线已经被剔除，但点Qx与Qk之间这部分还是需要聚合，虽然点Qx与Qk的序号不连续，但是可直接组成一个“聚合通道”。

图4 一个聚合通道

2）如图5所示，建筑物B1上点Qx与Qk之间线段的长度大于设定的阈值，并且与B2上对应的轮廓线部分和关联的两条最短邻近连线所围成的区域比较大，其面积大于设定的阈值。此时，Qx与Qk之间需要分解，两端单独构建“聚合通道”。

图5 多个聚合通道

4 建筑物群的渐进式聚合

4.1 渐进式聚合原理

建筑物群渐进式聚合的基本原理是基于最短邻近连线获取建筑群邻近关系后，从2个邻近建筑物的聚合开始，在新的聚合建筑物生成后，删除原来被聚合的2个建筑物；针对新建筑物和邻近建筑物重新构建最短邻近连线，获取“聚合通道”，随后渐进式地把新建筑物与邻近建筑物聚合，直至该建筑物群全部聚合完成。

4.2 详细算法

基于2个建筑物之间的“聚合通道”，就可以提取聚合后的新建筑物轮廓线。新建筑物轮廓线提取过程为：

1）如图6所示，按照建筑物轮廓点序号升序获取当前点，若当前顶点为“不可聚合的顶点”，则记录当前点并跟踪下一点。

2）若为“可聚合的顶点Pk”（如图6所示），需获取点Pk对应的最短邻近连线，然后按照顺时针方向选择与线段PkPk-1的夹角最小的边PkQj，并对点Qj所在建筑物的轮廓线顶点集合按照同样的方法跟踪，直至当前点为最左边点Si就可构成封闭环，最后将所有构成环的点移出集合R。

3）若2个建筑物之间只有一个“聚合通道”（图6），至此即完成新建筑物轮廓线提取；若如图6b所示，2个建筑物之间有多个“聚合通道”，则新建筑物存在内环，需按照上述提取环方法继续提取建筑物内环，直至R集合中的点无法构成环。

图6 提取内/外环

实现2个邻近建筑物聚合后，就可以对一个建筑物群进行聚合。基于最短邻近连线对建筑物群进行渐进式聚合具体步骤如下：

1）依据聚合距离阈值搜寻到一个建筑物子群。

2）判断建筑物之间的相交情况，插入交点；根据设定的插值点距离阈值加密建筑物轮廓线的顶点。

3）获取当前需要聚合的2个邻近建筑物，聚合后得到一个新建筑物B'。

4）更新建筑物群的空间邻近关系图，获取新建筑物B'的一个邻近建筑物，聚合得到新建筑物B''。渐进式地把新建筑物与其邻近建筑物聚合，直至当前建筑物子群聚合完成。

5）搜寻下一个建筑物子群，回到步骤2）。若所有建筑物子群处理完时，该过程结束。

5 实验与分析

5.1 实 验1

实验1选取了湖北省武汉市部分区域的数据作为实验目标，其地图比例尺为1:10 000。本文用Dot-Spatial+Visual Studio软件，实现并验证算法。图7 a是聚合前的原始建筑物数据。在本实验中，设插点间隔阈值变量为InterD，聚合距离阈值变量为d，删除内环面积阈值变量为Area，2个建筑物边线的方位差阈值变量为α，去除建筑物尖角的角度阈值变量为δ，构建聚合通道所设直线长度、折线长度和面积的阈值变量分别为L1、L2、DelArea。长度阈值的单位均为m，面积阈值的单位为m2。实验目标比例尺为1:100 000，根据国家地形图标准，此时建筑物长、宽和面积的最小尺寸分别为0.7 mm、0.5 mm、0.35 mm[27]，通过实验对比，将阈值设定为：α=30°，δ=5°，d=20，InterD=5，L1=60，L2=20，DelArea=400，Area=400。聚合结果如图7b所示，均为合理。

图7 建筑物群聚合前后对比图

为了对比聚合效果，使用同样的实验数据和参数设置，分别采用文献[28]提出的CDT方法、ArcGIS（10.2）软件中地图综合工具箱的多边形综合工具以及本文提出的方法对实验数据进行处理。其中使用Arc-GIS的多边形综合方法时，勾选了保留直角化特征选项。选取了实验结果的局部区域进行分析，图8a为原始建筑物数据，图8b、图8c及图8d的聚合距离阈值d均为2；图8e、图8f及图8g的聚合距离阈值d均为20，其中椭圆框区域为重点对比部分。对比实验的结果表明：

1)CDT方法用于小跨度的建筑物聚合时，可兼顾特征保持和避免邻近探测疏漏；反之则易出现邻近探测疏漏，产生图8e所示不合理凹部。

2)ArcGIS聚合方法在聚合方向差异较大的建筑物时，“夸大”了局部区域，如图8c所示。但是ArcGIS聚合方法用于大跨度的建筑物群聚合时，聚合结果相对合理，如图8f所示。

3)基于最短邻近连线的建筑物群渐进式聚合方法受聚合跨度影响最小，聚合结果较为合理，具体如图8d与图8g所示。

图8 不同聚合方法的实验效果对比

为了进一步说明本文所提方法的有效性，本文使用同样的实验数据和参数设置，将3种方法对图9a所示的原始建筑物群进行聚合，其中使用ArcGIS的多边形综合方法时，勾选了保留直角化特征选项。图9b为基于顶点线性插值的建筑物群渐进式聚合结果。若使用CDT法进行建筑物群聚合，如图9c所示无法同时构建B1与B4、B2与B3之间的连接三角形，导致B1与B4间无法基于连接三角形获取聚合通道进行聚合，聚合结果见图9d；使用ArcGIS（10.2）软件的聚合工具所得的结果见图9e。从实验结果的比较可以看出，使用本文所提方法可以得到更理想的结果。

图9 建筑物群聚合结果对比

5.2 实 验2

实验2选取了广州市局部地区的建筑物数据作为实验数据，原始地图比例尺为1:1 000，综合后地图比例尺为1:2 000。由于数据采集误差，该区域原始数据中存在较多建筑物群相交的情况。图10a为原始建筑物群，图10b为使用本文所提方法聚合后的建筑物群。由图10可知，本文提出的方法可以处理建筑物多边形之间存在相交和重叠空间拓扑关系的建筑物群聚合问题。

图10 实验结果（局部）

使用同样的参数，采用ArcGIS（10.2）软件中地图综合工具箱的多边形综合（aggregate polygon）工具和文献[28]提出的CDT方法对该实验数据进行处理，勾选了保留直角化特征选项。使用ArcGIS（10.2）软件的聚合工具所得的结果如图10c所示，从结果可以看出ArcGIS（10.2）软件的聚合工具虽然可以处理建筑物之间相交和重叠空间拓扑关系问题，但是有些聚合后建筑物整体轮廓的直角特征不明显；使用CDT法处理所得结果如图10d所示。从实验结果的比较可以看出，使用本文所提方法和CDT法在处理建筑物群的多边形数据里存在相交和重叠空间拓扑关系的聚合问题时，能够更好地保留建筑物整体轮廓的直角化特征。

6 结语

本文提出了基于顶点线性插值的建筑物群聚合的简易方法，在插值加密建筑物轮廓线顶点后，直接构建相邻建筑物顶点之间最短邻近连线用于分析、量测和计算建筑物群的邻近关系实现聚合；与基于CDT的建筑物聚合方法相比，该方法简化了计算过程，融合了三角网法[14-16]和缓冲区法[12-13]的特点。实验结果表明该方法实现了定性、定量获取建筑物群邻近关系进行聚合；处理了建筑物群的多边形数据里存在相交和重叠空间拓扑关系的聚合问题；能满足较大跨度的建筑物聚合，聚合建筑物群的结果合理且美观。目前，基于顶点线性插值的建筑物群聚合的简易方法通过探测相邻建筑物间的空隙完成建筑物群的聚合，仅能完成建筑物内部小岛屿的填充化简，后续将研究建筑物自身凹部细节的化简方法，实现建筑物群聚合和化简的一体化。