非荷载因素作用下的轴力修正计算
2022-03-11戴远俊陈大江
戴远俊,何 钦,陈大江
(1、珠海市金湾区建设工程质量监督检测站 广东珠海 519090;2、广东省建设工程质量安全检测总站有限公司 广州 510500)
0 引言
混凝土支撑对基坑的稳定性十分重要。若支撑轴力超过设计值,便可能会造成基坑失稳破坏。但目前在支撑轴力的监测过程中,会出现支撑轴力监测值远大于预警值以及设计值,但支撑仍然完整的情况。因此考虑对轴力监测值进行修正很有必要。
多年来,基坑轴力监测的准确性未能得到有效提高。叶万灵[1]较早发现混凝土支撑监测轴力远远大于设计值的问题,并通过室内模型试验和现场试验[2-5],对其进行验证(支撑轴力监测值大于实际轴力值)。在此基础上,学者们陆续开展对轴力监测值的修正研究。其中考虑温度与收缩徐变效应的修正是较为常见的方法[6-10],即在传统的轴力计算公式中单一考虑温度或收缩徐变效应,此法虽能适当修正监测所得轴力,但忽略了温度作用下弹性模量的变化及与混凝土徐变收缩共同作用造成的影响以及不同因素的影响大小。随着有限元方法的成熟,相关研究也逐渐采用有限元模拟支撑的轴力[11-12],该法能够较好地反映支撑受力的实际情况,但往往参数设计复杂,需结合现场情况进行修正;此外还有对测量仪器初始参数如钢筋计初始频率进行修正[13]等方法。虽然现有研究对影响支撑轴力的因素都做了相关探讨,但仅考虑单一因素的影响。在《公路钢筋混凝土及预应力混凝土桥涵设计规范:JTG 3362—2018》[14]中,提出考虑温度与收缩徐变影响这一做法,但未详细说明应做何种修正。因此现有的轴力修正方法仍有待研究。
为了提高混凝土支撑轴力监测的准确性,本文在前人研究的基础上考虑影响混凝土支撑轴力的因素,包括温度、混凝土徐变与收缩。结合基坑实测数据进行计算,探究了现有修正方法的修正效果,分析收缩徐变对支撑轴力的影响、修正值与预警值的关系,并对进一步研究提出了相关建议。
1 修正理论
1.1 修正理论概述
当前支撑轴力监测所使用的钢筋计或应变计采用应力应变关系原理,通常在计算轴力时无法排除非荷载因素引起的应变,因此往往造成支撑监测轴力大于实际轴力。目前对非荷载因素的修正方法包括温度修正、收缩修正和徐变修正等[6-7,10]。通过考虑温度膨胀,混凝土在长期荷载下的徐变以及收缩效应,在计算修正轴力时减去非荷载因素造成的变形,进而求得修正轴力。
1.2 温度影响作用
温度作用下混凝土以及应变计都会产生微小变形,但温度会引起多个参数的变化。为简化计算,现只考虑温度作用下的膨胀变形。由于混凝土与应变计的线膨胀系数不同,造成应变计与混凝土之间相互变形不协调,产生了应变偏差[6,10]。因此温度作用下对应变计的修正如下:
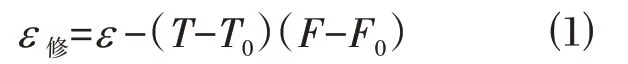
其中:F0=12.2 με∕℃,即钢弦的线膨胀系数为12.2 με∕℃;F0=10,一般情况下,混凝土的线膨胀系数为10 με∕℃。
1.3 徐变效应影响
在荷载的长期作用下,混凝土本身会发生徐变变形,对应变监测传感器产生干扰。在荷载作用下,轴向受力的钢筋混凝土支撑并考虑混凝土配筋率的徐变系数计算[7]可等效为式⑵:
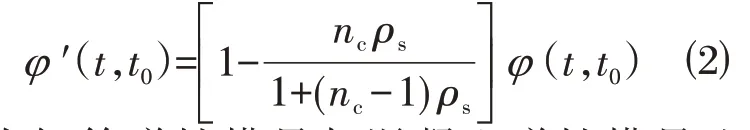
式中:nc为钢筋弹性模量与混凝土弹性模量比值;ρs为构件界面配筋率;其中φ(t,t0)计算参考文献[14]对预应力混凝土徐变相关量的计算:
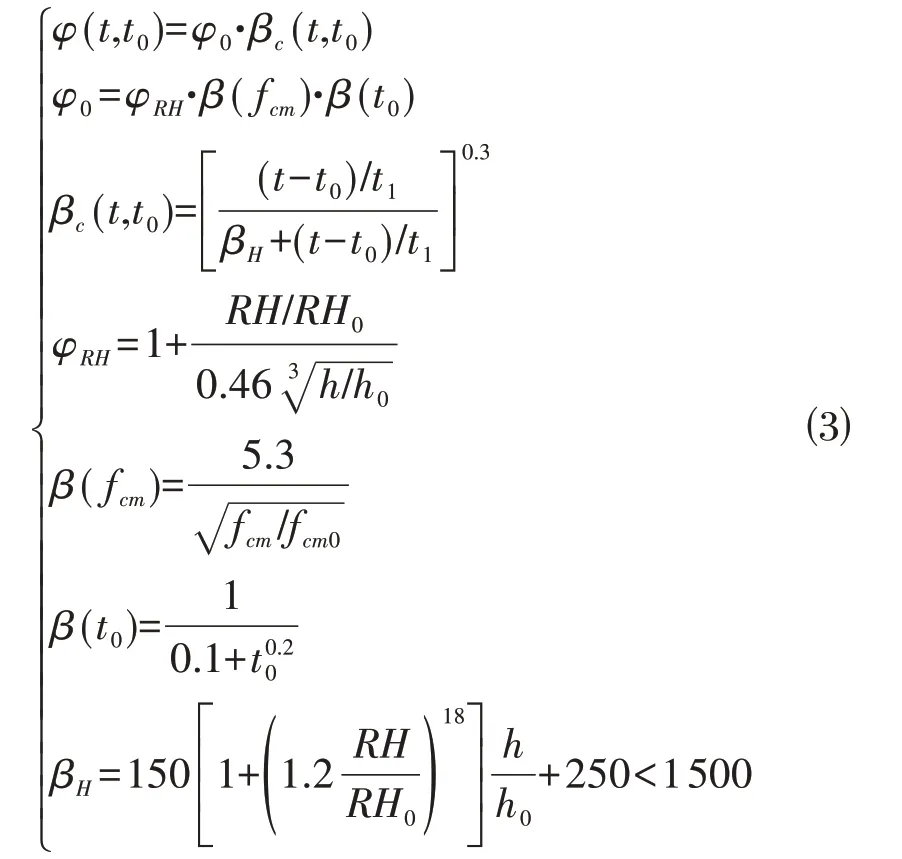
式中:t为计算时的龄期(d);fcm为强度等级为C25~C50 的混凝土龄期在28 d 龄期时的平均圆柱体抗压强度(MPa),fcm=0.8fcu,k+8MPa;fcu,k为龄期为28 d立方体抗压强度标准值(MPa);β RH为与年平均相对湿度相关的系数;RH为环境年平均相对湿度(%);h为构件理论厚度(mm),h=2A∕u;A为构件截面面积;u为构件与大气接触的周边长度;RH0=100%;h0=100 mm;t1=1 d;fcmo=10 MPa。
1.4 收缩效应的影响
在初期凝结、硬化、以及周围环境变化过程中会出现收缩现象,混凝土收缩属于混凝土自身性质,并非由荷载作用引起,同样会引起应变计的监测误差。目前应变收缩的计算公式参考文献[14]如下:
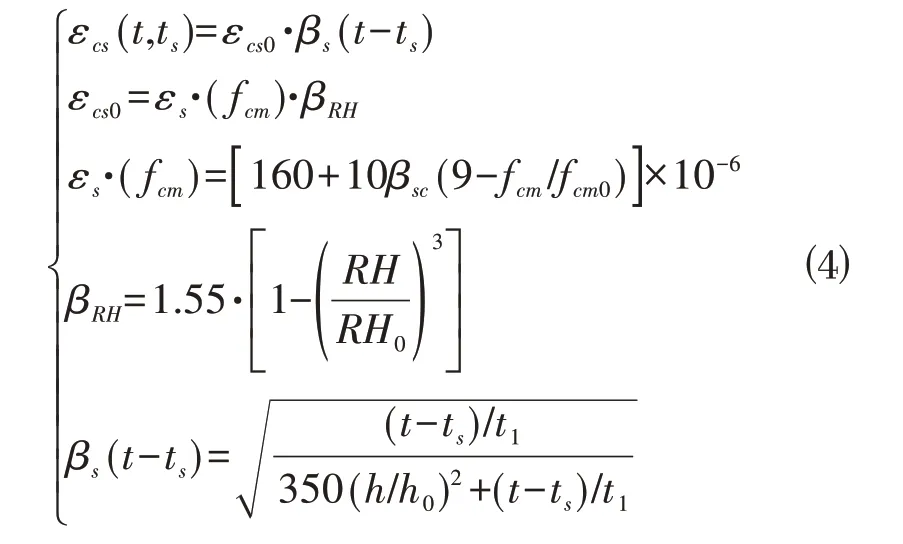
式中:ts为收缩开始时混凝土龄期(d),可假定为3~7 d;εts(t,ts)为变收缩开始龄期为ts,计算考虑龄期为t的收缩应变;εcso为名义收缩系数;βs为收缩随时间发展系数;βsc为对一般硅酸盐水泥或快硬水泥,βsc=5.0。
2 工程概况
2.1 工程概况
珠海某基坑面积为25 870 m2,基坑周长为676 m。基坑开挖深度为13 m,采用围护结构加两道支撑体系。混凝土支撑轴力监测传感器采用混凝土应变计,型号为JMZX-3001,应变计在浇注混凝土前绑扎在主钢筋上,并保证应变计与受力方向在同一轴线上。每个截面4 个角点或上下表面中间各布设1 个应变计。基坑围护结构开始施工时对支撑轴力进行监测。
2.2 支撑监测数据分析
在对基坑两道支撑进行连续监测后,监测过程中轴力异常变化如表1 所示,超出报警值的部分占报警值的比例如图1 所示。对于第一道支撑,其占比变化较明显,监测值超出报警值的比例最大为52%,远远超过报警值,最小比例约为1%。第二道支撑所占比例最大值达到90%,最小比例约为5%。但在基坑施工的整个周期中,两道支撑结构未发生破坏,基坑处于稳定状态。

表1 支撑轴力监测值与报警值Tab.1 Support Shaft Force Monitoring Value and Alarm Value

图1 轴力超出值与报警值之比Fig.1 Ratio of Axial Force Exceeding Value to Alarm Value
第一道支撑轴力随时间变化的趋势如图2⒜所示。可知,支撑轴力前期呈增长趋势,而后逐渐减小最终趋于稳定值。其中测点ZC10-1 在检测过程中最大轴力达到约34 000 kN。
第二道支撑轴力随时间变化的趋势如图2⒝所示。在基坑施工结束前,第二道支撑轴力在1 个月内增长迅速,后期变化逐渐平稳,并且最终轴力整体大于第一道支撑。在基坑施工过程中,测点ZC15-2 最大轴力达到37 835.1 kN,远远大于轴力设计值。在此期间基坑始终处于稳定状态。
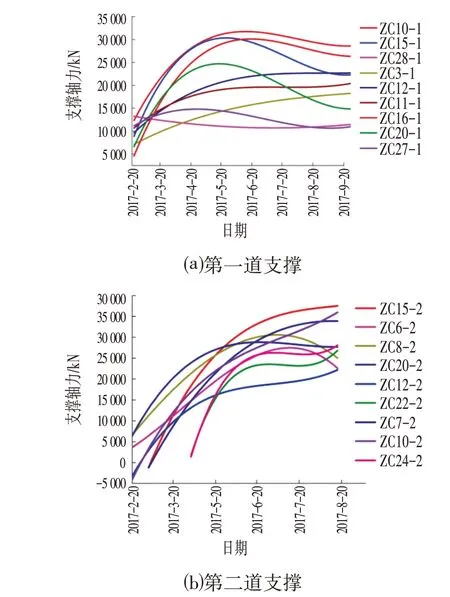
图2 轴力变化趋势Fig.2 Axis Force Change Trend Chart
根据上述分析结果可知,在基坑稳定状态下,部分支撑轴力的监测数据存在偏大的情况,甚至接近2 倍的设计值。但支撑仍旧完好,基坑未发生较大位移。分析上述现象出现的原因是轴力监测仪器只能测得混凝土的应变,但无法区分荷载因素引起的应变与非荷载因素引起的应变,造成监测轴力偏大的现象。而对于只有部分支撑轴力增大这一现象,笔者认为不同部位的支撑受力情况不同,收缩徐变也存在较大差异。但由于情况较为复杂,将不在此考虑本现象,只针对轴力偏大的支撑进行修正分析。
3 计算与分析
3.1 计算分析
根据上述修正公式⑴、⑵、⑷,综合考虑温度、收缩、徐变因素的修正公式以及轴力计算如下:

在现场轴力监测中,总应变即为应变计所测出的应变值。未对支撑轴力进行修正,监测值中包含非荷载因素产生的影响,导致监测值远大于荷载引起的实际轴力值。在修正计算时,为了更好的探究收缩与徐变造成的影响,只考虑混凝土收缩与徐变效应。利用上述修正公式对支撑轴力进行修正,以求得轴力的修正值。修正结果以及各种因素占比如图3、图4所示。
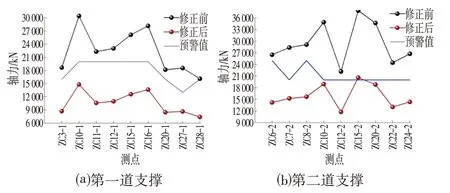
图3 监测值、修正值与报警值Fig.3 Monitoring Value,Correction Value and Alarm Value
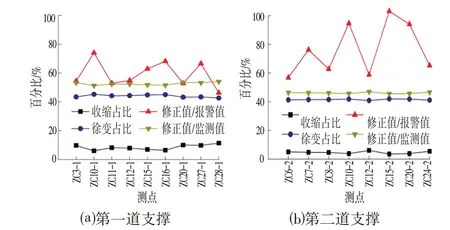
图4 修正值占比Fig.4 Correction Value Percentage Chart
3.2 修正分析
修正后轴力值与监测值以及报警值对比的曲线如图3⒜所示。可知,经过修正后的轴力明显小于监测值。其中ZC3-1,ZC20-1,ZC28-1预警值为16 000 kN,ZC27-1 预警值为13 000 kN,其余支撑预警值均为20 000 kN。图3⒜中所示的修正后轴力均低于设置的预警值。非荷载因素引起第一道支撑的轴力值、收缩徐变值、修正值与报警值之比如图4⒜所示。其中第一道支撑修正值与监测值之比约为51%~54%,收缩占比6%~11%,徐变占比42%~45%;修正后值占预警值比为42%~74%,均小于设置的预警值。
第二道支撑修正值与监测值以及预警值的对比情况分别如图3⒝、图4⒝所示。其中ZC6-2,ZC8-2预警值为25 000 kN,其余均为20 000 kN。第二道支撑修正值与监测值之比约为45%~47%,收缩占比3%~6%,徐变占比40%~42%;修正值与报警值之比约为56%~100.3%。出现比值100%的情况是由于支撑ZC15-2 修正后的轴力值仍高于报警值,因此比值超过100%,但最终结果处于设计值之内;对于两道支撑的轴力缩减幅度存在差异,其原因为第一道支撑存在时间较长,产生的收缩徐变的工期大于第二道支撑,因此其收缩徐变所占比例较大。
由上述两道支撑数据可得,考虑收缩徐变修正后,修正比例最高达到54%。表明收缩徐变效应对混凝土支撑确实存在一定程度的影响,并且徐变效应在非荷载因素中占主要地位,而收缩产生的轴力基本维持在3%~10%。但由于混凝土徐变与收缩的复杂性,修正后轴力与实际轴力的关系需要进一步研究。除此之外,支撑轴力的预警值设置也存在一定的不合理性,修正后的轴力一般约为预警值的60%~70%,因此也可以考虑重新设置预警值。支撑轴力的影响因素较多,对于不同类型支撑其参数也有所差别;并且轴力通过间接测量得到,想要获得精确的结果极其困难。本文只考虑几个影响较大的因素,因此存在一定的误差也是正常的。
4 结论
本文分析收缩与徐变因素对支撑轴力造成的影响,对珠海某基坑中轴力异常的支撑进行修正,比较修正前后的轴力值与预警值的关系。得到以下相关结论:
⑴在修正计算过程中,非荷载因素中收缩产生的轴力较小,约占总轴力的3%~10%;因收缩与混凝土的初凝期有关,在不同支撑中存在一定差异。
⑵徐变产生的轴力约占总轴力的45%~54%,对轴力造成的影响较大,是监测过程中的一个主要影响因素,并且徐变随时间而增长,其对中后期的轴力影响较大;除此之外,徐变涉及因素较多,其具体影响还有待继续研究。
⑶支撑轴力修正后,大部分修正值保持在一定范围内并低于预警值,但仍有部分支撑轴力在修正后仍接近或高于预警值。其原因在于徐变与收缩公式中实际涉及变量较多,并且对不同的混凝土支撑所涉及的参数也存在差别。基于上述修正结果与分析,现有的收缩与徐变收缩公式还需要进一步的探究。
