基于Gabor变换的GIS设备典型放电缺陷识别
2022-03-11孙景文孙艳迪孙承海
李 杰,汪 鹏,孙景文,孙艳迪,孙承海
(国网山东省电力公司电力科学研究院,山东 济南 250003)
0 引言
气体绝缘组合开关设备(Gas Insulated Switchgear,GIS)是电力系统中重要的电气设备,具有占地面积小、运行可靠性高、配置灵活、维护方便等优点[1]。随着电网的建设与发展,GIS 变电站的数目不断增加,其在电力系统中的应用越来越广泛[2],GIS的正常运行对整个电力系统的安全和稳定至关重要[3-4]。
绝缘缺陷是导致GIS 故障的重要原因,绝缘缺陷在一定电场下会导致局部放电的发生,引起绝缘的进一步劣化[5-6],在固体绝缘累积效应的作用下可导致绝缘击穿[7]。因此,做好对GIS 设备的状态评估与检修,及时发现绝缘故障并及时处理,能够有效预防较为严重的故障,对变电站乃至电网的稳定运行具有重要的意义。
由于GIS 的全封闭特性,其故障定位及检修工作比较困难且繁杂,停电检修难度大,需投入大量人力物力。局部放电检测是目前对电力设备绝缘状态常用的在线监测方式之一,当有局部放电发生时,立刻采取预警与行动可以有效预防严重事故的发生,提高电力系统的可靠性[8]。不同类型放电形式下绝缘的劣化机理不同,进而对GIS 绝缘造成不同程度的损伤,其局部放电信号也会呈现出差异,因此对GIS 局部放电进行模式识别是GIS 绝缘状态评估的重要环节[9-10]。
目前各类机器学习算法被应用到GIS 设备局部放电模式识别范畴,并取得了较好的效果。文献[11]将GIS 信号的特高频与超声局部放电特征量融合后,再使用MKL-RVM 进行模式识别,识别率高于单一的超高频和超声波参数的识别率。文献[12]使用局部放电谱图的偏斜度、陡峭度、互相关系数等作为GIS局部放电特征参数,利用最小二乘支持向量机识别局部放电类型。文献[13]将GIS 不同绝缘缺陷的局部放电时域波形图像通过预处理并转化为一维数据,使用一维卷积神经网络实现了对局放缺陷的准确识别。文献[14]使用最小距离分类器,基于GIS 局部放电灰度图像的特征能够实现对4 种不同放电类型的识别。
目前国内外对GIS 特征提取与模式识别已有较多研究,也取得了不错的效果,但较多都是基于局部放电参量或二维局部放电图谱进行的特征提取与识别,较少有研究对局部放电三维图谱进行特征提取。由于三维图谱包含多个周期的局部放电信号,其偶然性与分散性较小,更能反映放电的典型特征,目前对基于时间序列的局部放电状态量信息挖掘不充分。
因此,根据GIS 典型缺陷的特高频局放信号,采用常被应用于图像处理的领域中的Gabor 变换方法[15],对局部放电脉冲序列分布(Phase Resolved Pulse Sequence,PRPS)三维图谱进行Gabor 变化,利用变换系数实现不同方向的有效分解,对分解得到的子图提取特征量作为模式识别的输入量。采用不同的机器学习方法,根据Gabor变换后提取的特征量对不同的放电类型进行识别和诊断。
1 局部放电三维PRPS图谱的获取
设备的制造、安装、运输等过程均有可能会产生气泡、悬浮导电物质、尖端毛刺等缺陷,这些缺陷在一定电场下会导致局部放电的发生[6]。为在实验室模拟这些绝缘缺陷,选择金属微粒放电、悬浮电位放电、金属针尖放电3 种典型GIS 内部局部放电缺陷,在实验室制作了相应的缺陷模型,如图1 所示,将其放入GIS模拟器中进行局部放电试验。
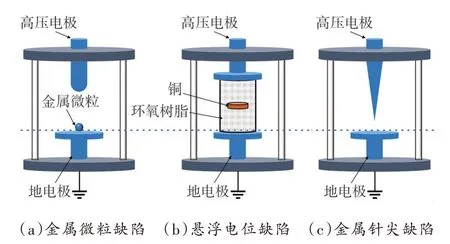
图1 典型局部放电缺陷模型
目前常见的局部放电检测方法主要有脉冲电流法、特高频检测法、超声波检测法、化学检测法、光检测法等。其中,特高频检测法(Ultra High Frequency,UHF)通过局部放电发生时脉冲电流所产生的高频电磁波来监测局部放电,可以在设备不停电的情况下实现带电检测或者在线监测,抗干扰能力较强,可以有效地抑制一些频率较低的背景噪声[16]。因此,试验时选用特高频法检测放电信号,进一步对监测得到的信号进行处理从而识别设备存在的缺陷种类。对采集到的局部放电信号可以进一步绘制局部放电脉冲序列分布PRPS 三维图谱。PRPS 三维图谱包含多个周期内的局部放电信息[17],包含很多能够表征放电类型的特征,对其进行有效提取能够提高识别准确率。
对每一种典型缺陷采集60 组信号,每一组信号包含50 个工频周期,对0°~360°相位开窗,将每个周期分为100 个相位窗口。随后,绘制出典型缺陷模型的幅值-相位-周期三维PRPS 图谱如图2 所示,柱状图的高度即z轴表示信号幅值,x轴表示相位,y轴表示信号周期数。

图2 典型放电缺陷的PRPS图谱
从图2 中可以明显看出,对于金属微粒缺陷,其放电点较为稀疏,整体放电重复率不高,以较大幅值的放电脉冲为主,在相位分布上较为分散;对于悬浮电位缺陷,其整体放电不密集,放电重复率也不高,集中在0°~45°、90°~135°、185°~225°和275°~315°相位区间,在0°~45°与185°~225°相位区间以密集小幅值放电为主,在90°~135°与275°~315°相位区间以稀疏大幅值放电为主;对于金属针尖缺陷,整体放电重复率较高,正半周期放电幅值大而稀疏,但也有部分稀疏的小幅值放电,负半周期放电十分密集,放电幅值波动不大。
图2 表明三维PRPS 图谱在幅值大小、放电次数与相位分布的特性存在一定的差异。为了后续进一步利用机器学习的方法通过放电图谱对不同放电类型进行识别,需要考虑如何量化图谱的特征,使其转化为数字量。
2 二维Gabor变换
Gabor变换是一种短时Fourier变换,相比于传统的Fourier变换,Gabor小波具有良好的时频局部化特性且对图像的边缘十分敏感,因此常被应用于纹理识别[18-19]。近年来,在人脸识别领域,对图像灰度进行多尺度、多方向的Gabor小波变换逐渐成为主流思路之一,得到了广泛的应用[20-21],这是因为Gabor 小波可以提取图像特定区域内的多尺度、多方向空间频率特征,局部关键特征被放大、增强[22]。由于不同缺陷的局部放电PRPS 图谱中的局部关键特征也存在显著差异,因此也采用Gabor变换的方式对图像进行特征提取。
Gabor 变换的基本原理为:根据Heisenberg 测不准原理,任意测量精度都不能同时在时域和频域都获得[23],其下界是时域窗口可以达到的最小面积,高斯函数即在此极限值。因此选择高斯函数作为窗函数可以使得Gabor 变换平衡时域和频域分辨率的矛盾,同时获得二者的较高值。
设需要进行变换的变量为f(t),且f∈L2(R),L2(R)代表实数轴上平方可积的函数空间[24],则根据Gabor变换的定义,Gabor变换表达式为
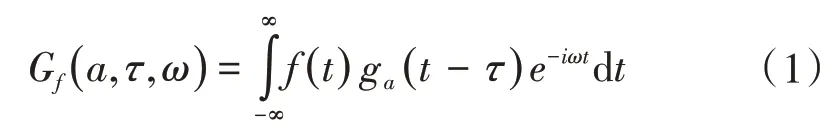
二维Gabor 滤波器是应用最广泛的纹理特征提取工具,目前在人脸识别、虹膜识别[26-27]等方面的应用都取得了不错的效果。二维Gabor滤波器的公式的复数表达形式为:

式中:x、y分别为图像中任意点位置的横纵坐标;λ为波长;θ为波器方向角与y轴的夹角;ψ为相位偏移;σ为高斯包络沿x 轴与y 轴的标准方差;γ为空间的宽高比。
为了使得所设计的二维Gabor 滤波器对于不同典型缺陷的PRPS 图谱具有较好的特征提取能力,还需要合理选择Gabor滤波器的参数,由这些参数限定的滤波器所提取出的能够表征放电类型的特征才具有较高的可区分度。因此,经过多次尝试,选择λ=4,且θ=0°,45°,90°三种方向变换下的Gabor 变换子图作为后续研究对象,对图2 中的PRPS 图谱分别进行二维Gabor 变换,每个PRPS 图谱进行一种尺度三种方向共3种变换,得到GIS 各缺陷模型下局部放电图像的分解如图3所示。
图3 中各子图分别为金属微粒缺陷、悬浮电位缺陷、金属针尖缺陷的局部放电PRPS 谱图经Gabor变换后,在θ=0°,45°,90°三种方向变换下分解图。
观察图3 中Gabor 变换后的分解图,并与图2 中各缺陷模型的原始局部放电图像对比,可以发现,经过Gabor 变换后,原始图像的幅值起伏基本保留,局部细节十分明显,可以清楚地看到局部放电发生部位的尖刺,因此分解后的子图更有利于提取有效的特征参量。

图3 PRPS图谱经Gabor变换后的分解
选用统计法中的Tamura 纹理特征与灰度-梯度共生矩阵,对PRPS 经Gabor 变换后的分解图图像的纹理特征进行描述:首先计算得到粗糙度、对比度、方向性、线性度、规则性和粗略度共6 个Tamura 纹理特征;灰度共生矩阵指图像中两个像素出现的联合频率分布,再进一步根据此求取15 个对于反映图像纹理有帮助的统计量:自相关、对比、相关、集群突出、簇遮蔽、差异性、能量、熵、均匀性、最大概率、平方和、总和平均值、总和方差、总和熵和差异方差。形状特征方面,求取局放图谱的Hu 不变矩获取7 个特征量和6 个Zernike 矩特征量。这样对于每个分解图提取34 个特征量,如表1 所示,每个局放PRPS 图谱获得共计102个特征量。

表1 Gabor变换后对分解图提取的纹理和形状特征量
3 基于机器学习的放电类型识别
3.1 放电数据样本的层次聚类分析
每种缺陷类型的PRPS 图谱在λ=4 且θ=0°,45°,90°三种方向下可以变换得到3 幅变换子图,每张子图可以提取纹理特征及形状特征共34 个。因此,对于每张原始PRPS 图谱,其都对应一种典型GIS 放电缺陷,包含102 个Gabor 变换后提取出的特征量,这些特征量构成了模式识别的向量空间。
在根据这些提取的特征量对不同放电缺陷进行识别之前,需要对采用这种方法的可行性进行分析,即应首先明确这些特征量是否能够区分不同的典型缺陷。因此,基于上述选取的102个特征量,对180个放电数据样本进行聚类分析。聚类是根据一定的准则将未知样本集划分为不同类别的过程,是典型的无监督学习问题。常见的聚类算法有:层次聚类法、K均值聚类算法、自组织映射(Self-Organizing Maps,SOM)聚类算法和模糊C均值聚类算法等。采用使用较广泛的层次聚类法对放电数据样本进行聚类分析。层次聚类法是最基本的聚类方法,可分为凝聚法和分裂法,本文采用凝聚层次聚类法。假设样本矩阵包含m个样本,凝聚层次聚类法的计算步骤如图4所示。

图4 凝聚层次聚类法的计算步骤
将金属微粒缺陷、悬浮电位缺陷和金属针尖缺陷的放电样本分别编号为1~60、61~120 和121~180,按照上述方法对不同缺陷的放电数据样本进行聚类后,得到的类别划分如表2 所示,聚类谱系如图5所示。

表2 不同缺陷放电数据的聚类结果
表2 表明,层次聚类法在放电缺陷与放电数据样本之间的对应关系未知的情况下,聚类的划分结果与实际放电缺陷编号一致,这意味着Gabor变换后提取的特征量与不同放电缺陷存在紧密的联系,能够很好地表征不同缺陷的放电特征并区分不同缺陷类型。图5 也清晰地表明,不同放电数据样本之间的相似度也存在较大差异,这验证了通过特征量对放电数据样本进行识别是可行的。

图5 放电数据样本的聚类谱系
3.2 典型放电缺陷的识别
聚类的结果证明了通过Gabor 变换后提取的特征量进行识别是可行的,由于聚类属于机器学习范畴中的无监督学习,其只能对不同的样本进行区分,无法对其具体类型进行识别,因此需要使用其他方式对放电缺陷进行识别。
选取150 个局放样本作为训练集,30 个样本构成测试集,采用不同的机器学习算法进行局部放电的模式识别。
常见的机器学习分类算法有以下几种:如K 近邻(K-Nearest Neighbour,KNN)算法[28]、朴素贝叶斯算法[29]、决策树算法[30]、支持向量机(Support Vector Machine,SVM)算法[31]、人工神经网络[32]等。不同的分类算法对于同一数据集的表现效果不一样,具有各自的优点和缺点,本文对于同一个数据集,采用不同的机器学习算法,对比不同算法的识别效果。
首先对包含150 组样本的训练数据集,使用不同机器学习算法进行训练,同时进行交叉验证,方式为5-fold cross-validation,其具体方法为:将原始数据分为5 个子集,每次将一个子集作为验证集,其他4组子集数据作为训练集,这样重复进行5 次,得到5个学习模型及每次训练后的模型对验证集的识别结果,最终得到每个模型综合识别准确率。
训练完成后,对测试集进行测试:根据各种分类模型对于150组样本的训练效果,选择5种较为典型的算法,将测试集中30 个样本的特征量作为输入量输入训练好的分类模型中,得到输出量1、2、3 其中的一个数字,分别表征金属微粒放电、悬浮电位放电和金属针尖放电,从而实现GIS 局部放电缺陷的识别。整个识别的过程如图6所示。

图6 典型缺陷类型识别过程
得到不同算法的识别结果如表3 所示。表3 中的识别结果表明,虽然精细高斯SVM 算法对缺陷的识别率较低,仅有80%,但决策树、KNN 算法与神经网络对金属微粒放电、悬浮电极放电与金属微粒放电这三种典型GIS 缺陷的整体识别准确率高达100%,核朴素贝叶斯算法的识别准确率也可达93.3%。这表明:使用Gabor 变换对GIS 特高频局部放电PRPS图谱进行提取的纹理特征量和形状特征量能够较好地刻画放电三维图谱特征,且不同的放电缺陷图谱特性差异性较大,该方法能够有效识别典型放电缺陷。

表3 不同分类算法的识别结果和准确率 单位:%
4 结语
通过试验提出了一种GIS 设备放电故障的诊断方法,通过特高频检测法获取了GIS 内不同放电模型的局部放电信号,随后使用二维Gabor 滤波器,通过Gabor 变换提取了GIS 局部放电三维PRPS 图谱的纹理和形状特征量。将提取出的特征量作为机器学习算法的输入量,对分类模型进行训练以对不同放电类型进行识别。结果表明:SVM、决策树、核朴素贝叶斯和KNN 算法与神经网络对3 种放电类型的识别准确率均较高,利用Gabor变换对图谱提取出的特征量与放电类型的相关度较高并能体现出不同放电类型之间的差异性。该识别算法可为GIS 放电故障类型诊断提供一定的参考。该方法能够实现GIS 故障的放电缺陷类型识别,提高电力系统故障诊断的智能化水平。
