基于等几何分析的自由曲面壳体包容式节点力学分析方法*
2022-03-11孙远韬王斌贺秦仙蓉
孙远韬 王斌贺 张 氢 秦仙蓉
同济大学机械与能源工程学院 上海 201804
0 引言
桁架结构由于其结构简单、承载能力强、加工方便且自重轻的优势在起重机械中得到了广泛的应用。节点的力学性能对桁架结构的承载能力和受力起到了至关重要的作用。但目前常见的节点形式存在应力集中,抗疲劳能力差等问题。故一种新型管相贯节点——包容式节点被提出应用[1],如图1所示。

图1 包容式节点
目前包容式节点已在某风电安装平台、起重机、RMG等项目中得到初步应用,取得良好效果,展示出较好的力学承载能力和抗疲劳性能。但目前包容式节点的设计仍处于经验设计阶段,其曲面形状具有较大随机性,限制了包容式节点的进一步发展。为进一步发挥包容式节点的优势,将曲面形状采用自由曲面的形式进行描述并进行灵敏度分析、形状优化等研究必不可少。
常规的有限元手段在进行自由曲面壳体形状优化时存在容易出现网格畸变,在优化过程中需不断重复划分网格,无法获取灵敏度的解析解等问题,限制有限元方法在包容式节点曲面优化设计中的应用。而由Hughes等于2005年提出的等几何分析(isogeometric analysis,IGA)[2]是一种采用几何模型自身的NURBS函数作为形函数的有限元分析方法。其将CAD、CAE一体化,在优化过程中无需划分网格,不因对几何模型的离散造成精度损失,能给出自由曲面灵敏度的全解析解,且优化结果较为光滑,适用于进一步对包容式节点自由曲面的优化设计。
因此,本文基于对包容式节点曲面优化设计的需求,研究等几何分析在壳体自由曲面分析中的应用,并建立包容式节点的曲面模型,采用等几何分析方法对不同厚度的包容式节点自由曲面进行力学分析,研究不同厚径比对等几何分析结果的影响,并采用有限元仿真结果进行验证,为接下来对包容式节点曲面的优化设计提供力学分析手段。
目前,国内外对于等几何分析在壳体分析领域的研究包括:Kiendl.J等[3]基于Kirchhoff-Love假设建立了三自由度的等几何壳单元,对相关理论进行推导后建立一个基于CAD程序的等几何分析程序验证该方案的有效性。Nguyen[4]将T样条曲线应用到等几何分析方法中,并采用实例说明该方案允许局部细化。张升刚等[5,6]研究了Reissner-Mindlin退化壳理论在等几何分析中的应用,并研究了基于壳体等几何形状灵敏度的曲面优化。李新康等[7]进一步研究了基于Kirchhoff-Love理论的等几何分析在薄壳静态问题中应用,并对NURBS单元的阶次与数量与该方法精度之间的联系进行了分析。常峰[8]分析不同罚函数对Kirchhoff-Love板壳等几何分析方法的精度影响,并将等几何分析理论应用到断裂力学当中。袁沛等[9]基于Kirchhoff-Love理论建立了非结构化T样条薄壳单元,并对其在模态计算和弹性变形分析中的应用进行了研究。
1 NURBS方法基本原理
NURBS方法是一种特殊的样条曲线,起源于航天领域对于曲面设计的要求。其从数学形式上可写为控制点的插值分段有理多项式形式,与常见的拉格朗日等插值方式不同的是,NURBS曲线并非经过控制点,其控制点落在拟合曲线外侧,即凸包性。同时,一段NURBS曲线形状仅与k+1个控制点相关(k为NURBS曲线的阶次),即局部性。几何不变性、参数连续性等也是NURBS方法被广泛应用于描述曲线曲面形状的重要原因[10]。
NURBS曲线通常可写为以下分段有理多项式矢函数形式
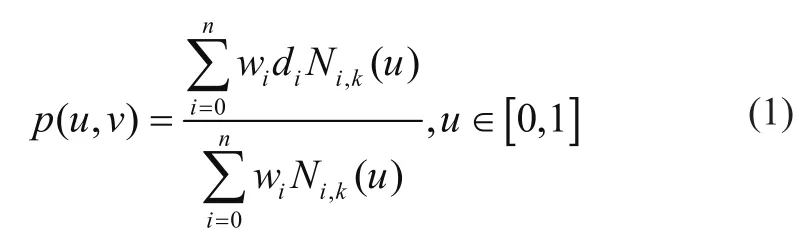
式中:Ni,k(u)为k次B样条规范基,其具体数值一般根据节点矢量U=[u0,u1,…un+k+1]由de-door递推公式获得为
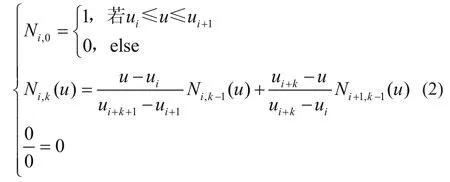
此外,di(i=0,1,…n)为控制顶点,wi(i=0,1,…n)为控制点顶点对应的权因子。
NURBS曲线的表现形式如图2所示。
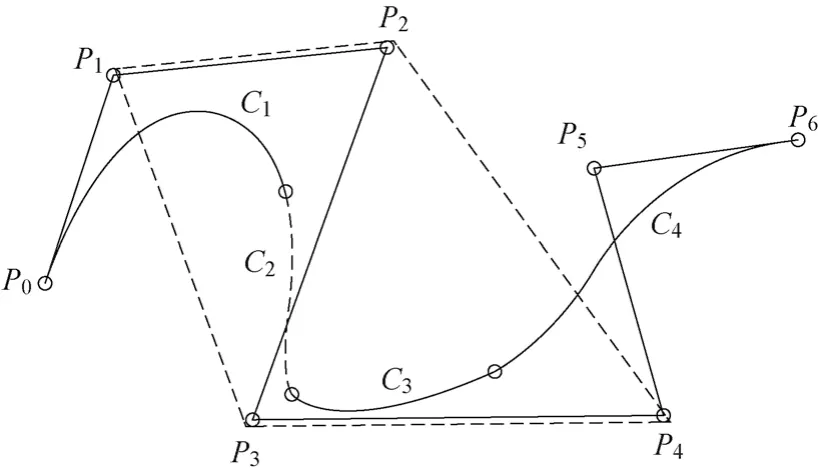
图2 NURBS曲线图
但在程序中采用de-door计算NURBS的基函数需要大量运算,因此,在实际运算过程中可以通过公式推导将NURBS曲线写为矩阵表示形式。同样条件下,采用矩阵表示形式可以提高运算速率20倍以上。
NURBS曲面一般可写为
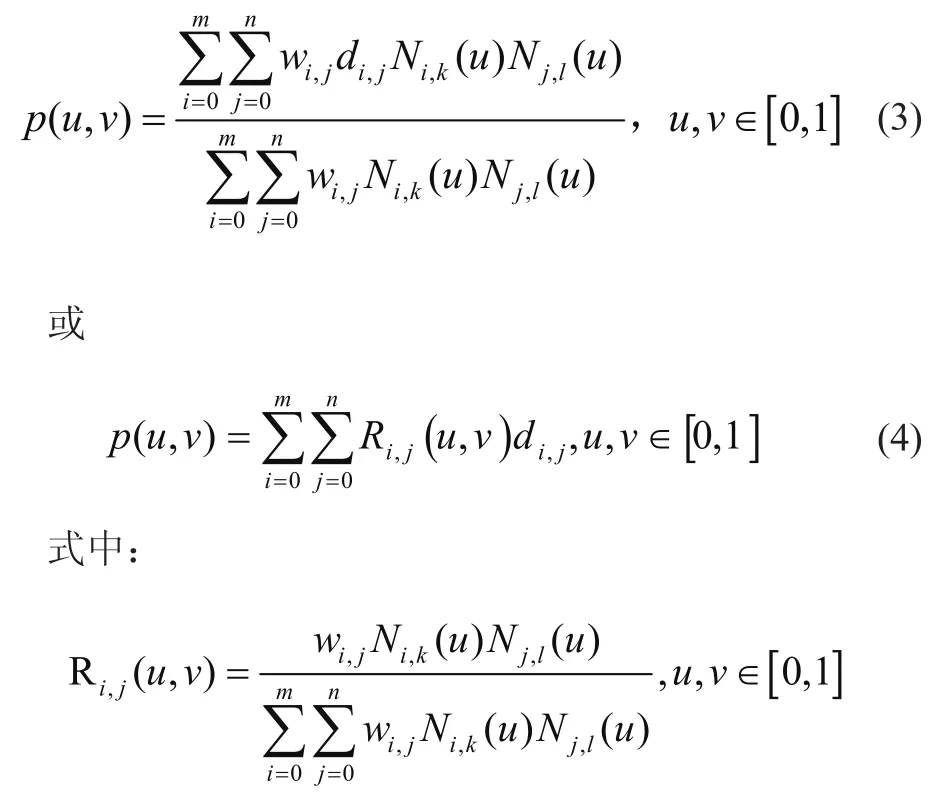
式(3)、式(4)中:dij(i=0,1,…m;j=0,1,…n)为拓扑矩形阵列,形成一个控制网格。wij(i=0,1,…m;j=0,1,…n)为其对应的权因子。Ni,k(u)(i=0,1,…m)和Nj,l(u)(j=0,1,…m)分别为u向k次B样条规范基和v向l次B样条规范基,分别由节点矢量U=[u0,u1,…um+k+1],V=[v0,v1,…vn+l+1]经de-door递推公式获得。
NURBS曲面的表现形式如图3所示。绿色曲面为NURBS曲面,红色星形点为NURBS曲面对应的控制点。事实上,由于几何连续性以及精度方面的优势,工程中自由曲面一般采用NURBS方法进行描述,并于1991年NURBS方法被国际标准化组织定义为描述工业产品几何形状的唯一数学方法。
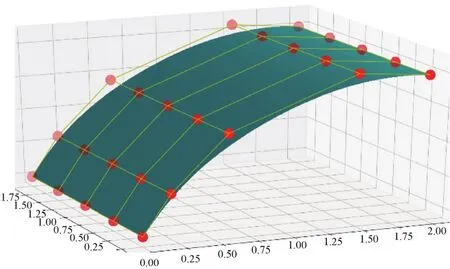
图3 双三次5×5控制点曲面
2 基于Reissner-Mindlin退化壳理论的等几何分析
2.1 基础理论
Reissner-Mindlin退化壳单元具有5个节点自由度,u,v和w以及绕u,v两轴的转动自由度,相较于Reissner-Mindlin单元去除了uv平面内的旋转自由度,Beason[11]采用了大量实例证明了将Reissner-Mindlin退化壳单元应用于等几何分析的可靠性。曲面壳体坐标系的定义如图4所示。
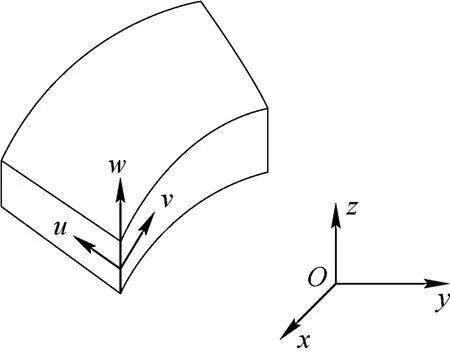
图4 曲面壳体坐标系
等几何分析采用描述曲面自身的NURBS函数作为插值形函数,故有壳体上任意一点坐标的表示为
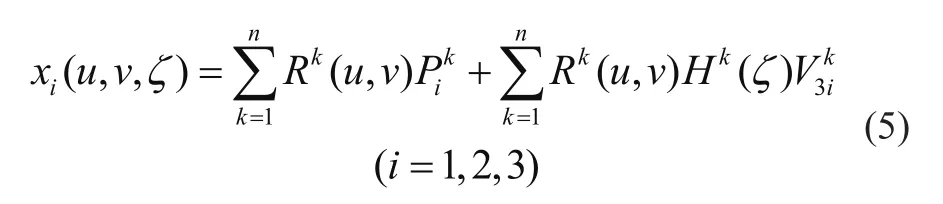
式中:xi(u,v,ζ)为壳体内一点坐标的第i个维度,为控制点对应的法向量,Hk(ζ)为壳体法向插值形函数,Rk(u,v)为NURBS曲面的k次有理基函数。
任意一点的位移为
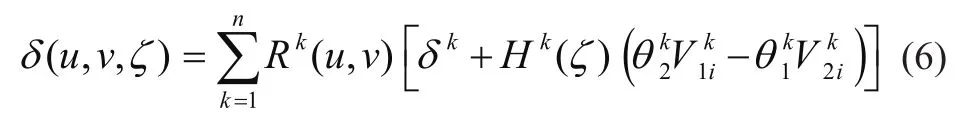
式中:kδ为第k个控制点对应的位移,为控制点对应的切向量,则为控制点绕单位向量的转角。
由此可得,等几何分析对应的应力应变矩阵为
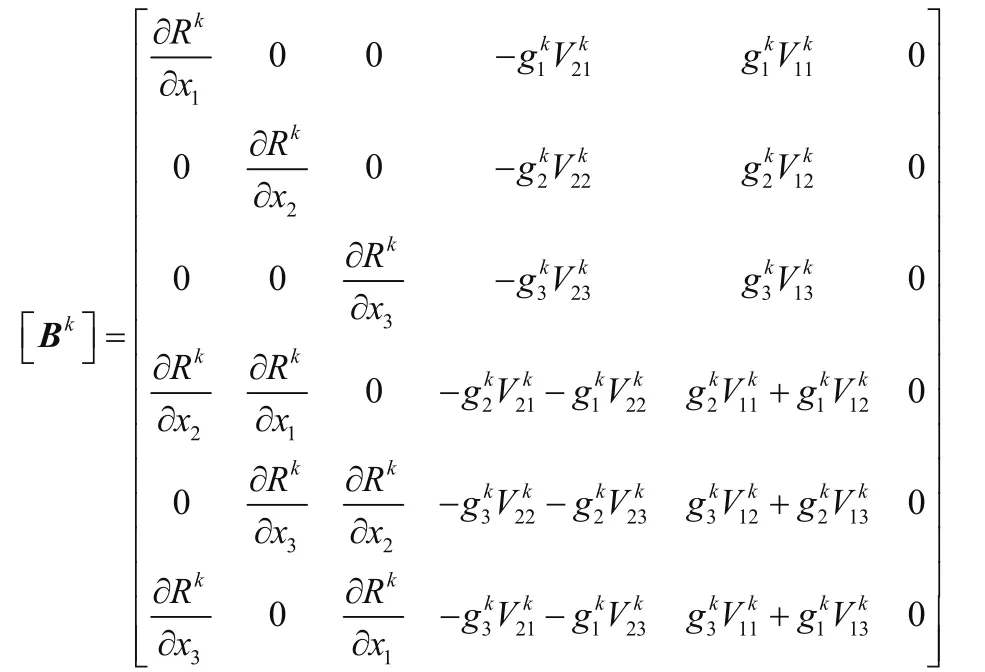
2.2 等几何分析刚度矩阵的计算
有限元分析的单元刚度矩阵一般为
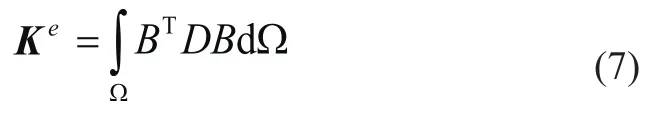
等几何分析方法采用等参元思想,其Reissner-Mindlin壳单元的单元刚度矩阵为
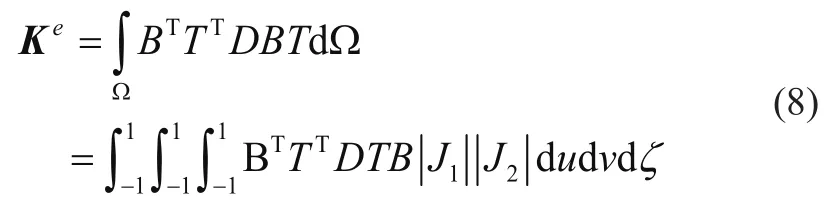
式中:[T]为转置矩阵,将单元刚度矩阵从局部坐标系转置到总体刚度矩阵的坐标系下。
其转置矩阵T为
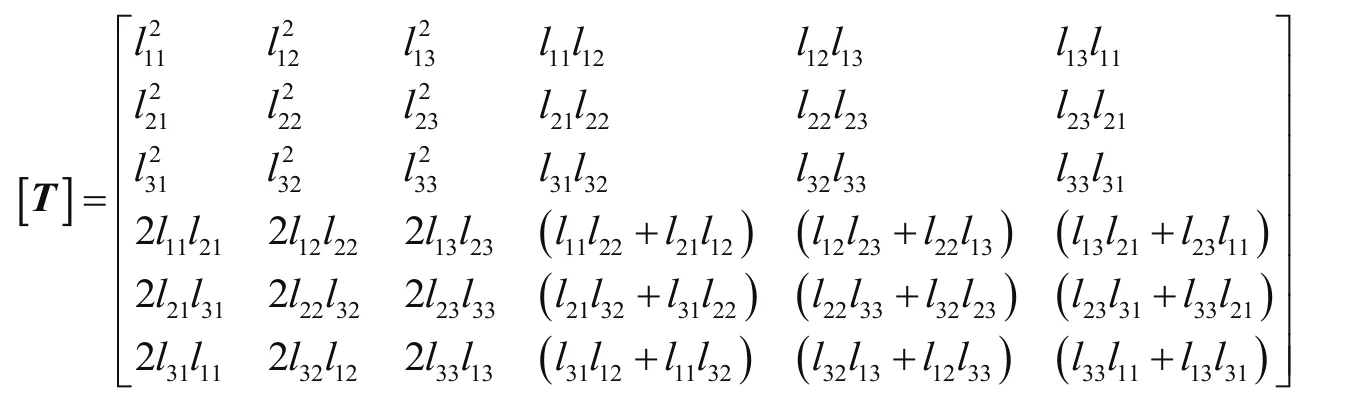
式中:lij为积分点对应的切向量或法向量Vi相对于整体坐标系下的3个坐标轴的方向余弦。
3 等几何分析在包容式节点中的应用
3.1 等几何分析的程序实现
基于Reissner-Mindlin退化壳理论的包容式节点自由曲面等几何分析由以下几个步骤组成:
1)基于NURBS方法建立包容式节点的自由曲面模型。一般可通过逼近和插值获取包容式节点对应的NURBS曲面模型,也可直接设定NURBS参数建模对应自由曲面模型。
2)输入NURBS曲面模型数据 不同于有限元方法的需要根据曲面坐标通过划分网格来划分单元,等几何分析可直接采用几何模型自身NURBS网络进行单元划分,无需在几何形状改变后重新划分网格,也不会因CAD、CAE模型之间的转化造成误差。它一般通过NURBS曲面自身的节点矢量划分单元,并对单元进行编号,记录每个单元对应的控制点编号。计算控制点对应的曲面最近点(u,v)坐标,计算该坐标的法向量作为控制点对应的法向量。赋予所有单元计算单元刚度矩阵所需数据。如图5所示等几何分析单元1以及其对应的控制点。
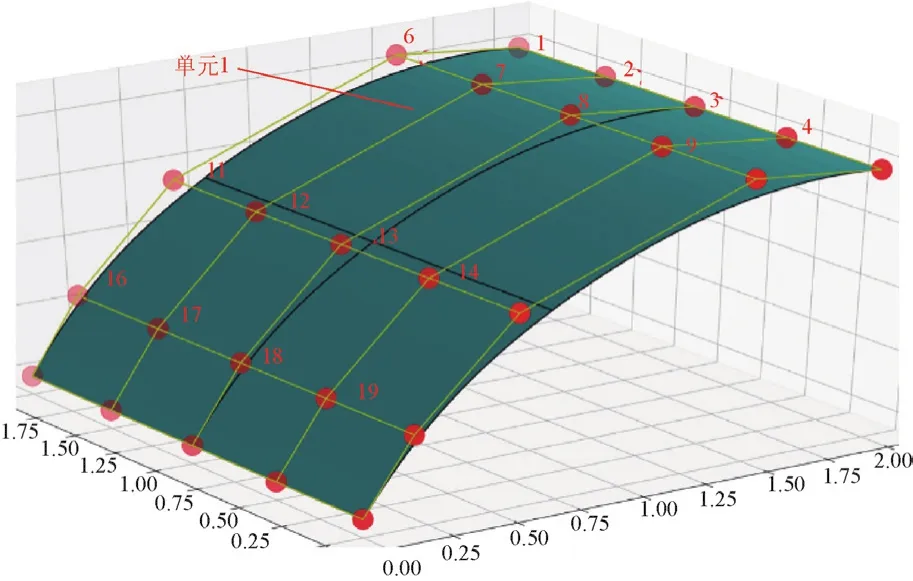
图5 等几何分析单元与控制点对应图
3)遍历所有单元 在单元参数域中取高斯积分点并计算对应的R基函数的值以及其对于参数u,v的导数、雅克比矩阵、应力应变矩阵、弹性矩阵、转置矩阵等,通过高斯积分公式进行积分运算获取单元刚度矩阵。
4)组装总体刚度矩阵 遍历所有单元,根据控制单在单元刚度矩阵以及总体刚度矩阵中的对应位置,将单元刚度矩阵组装到总体刚度矩阵之中。
5)施加载荷 根据载荷的类型及大小生成对应的总体载荷矩阵。
6)施加约束 根据所约束控制点的自由度对总体刚度矩阵进行对角元素置一法处理。
7)采用稀疏矩阵运算库对KU=F进行求解,所获得的位移向量U即为各个控制点对应的位移值。通过NURBS函数的R基函数进行插值处理便可获得曲面上任意一点的位移值。
3.2 包容式节点的等几何分析
包容式节点作为一种曲面壳体结构,一般由凸包和半圆柱面组成,如图6所示。

图6 包容式节点实物图片
采用曲面拟合的方式建立起包容式节点的NURBS曲面模型,为方便展示结果,采用Python对NURBS曲面表面均布采点可视化,如图7所示。
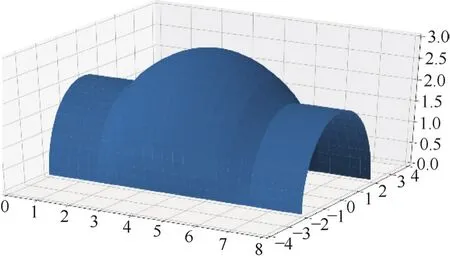
图7 包容式节点NURBS曲面模型
所采用包容式节点NURBS曲面模型参数为:长度L=8 m,半圆柱面半径R=2 m,凸包高度H=1 m,厚度=0.2 m。控制点数目20×20,且曲面为双三次NURBS曲面。力学参数设置为:弹性模量E=2.06×1011Pa,泊松比ε=0.3。本质边界条件为约束其4条边的所有自由度,自然边界条件为在包容式节点中部施加F=3 000 N的集中载荷。采用等几何分析对该包容式节点模型进行分析,对NURBS曲面模型表面局部采点,并记录位移值,为便于与有限元分析结果进行比较,采用Python将其可视化,如图8所示。
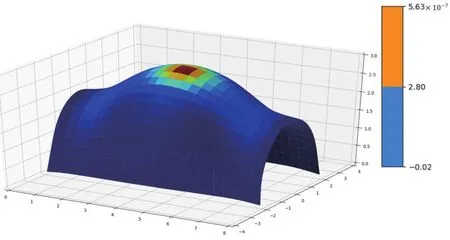
图8 等几何分析仿真结果图
采用有限元方法在相同条件进行力学分析可获得如图9所示结果。

图9 有限元S仿真结果图
如图8、图9所示,两者位移分布基本一致,采用等几何分析算出最大位移值为5.62×10-7m,采用Abaqus分析最大位移值为6.28×10-7m。两者结果基本一致。
采用相同双三次NURBS曲面模型,厚度分别取为0.01 m、0.1 m、0.15 m、0.2 m、0.25 m、0.3 m、0.5 m的包容式节点自由曲面模型进行试验。通过等几何分析以及有限元方法对其进行力学求解,可获得其z方向最大位移值如表1所示。

表1 IGA与Abaqus结果对照表 m
由表1可知,当包容式节点厚度较大时,IGA结果与Abaqus分析结果较为接近。其与有限元分析结果的误差如图10所示。
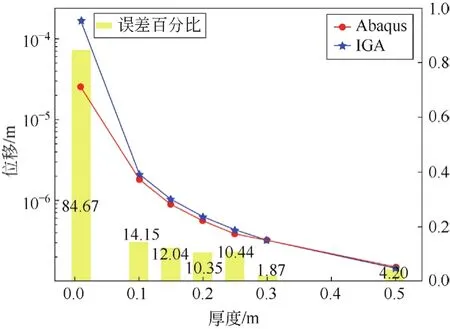
图10 误差随包容式节点厚度分布图
图10中红色折线图为Abaqus仿真结果位移值,蓝色折线图为等几何分析仿真结果,黄色柱状图为误差值。由图10可知,采用基于Reissner-Mindlin退化壳理论的等几何分析方法对半径L=1的包容式节点进行分析时,当其厚径比小于0.005时其结果误差较大。而当其厚径比大于0.05时结果与有限元方法分析结果较为接近,当其厚径比大于0.15时,采用该方法的分析结果基本与有限元方法的分析结果一致。目前,主要应用的包容式节点厚径比为0.2左右,故该方法适用于包容式节点的力学分析。
4 结论
本文简要地介绍了包容式节点在工程中的应用价值以及其进一步发展所遇到的问题。说明了对包容式节点自由曲面模型进行等几何分析方法研究的必要性,并通过建立基于Reissner-Mindlin退化壳理论的等几何分析壳单元模型,给出了相应的单元刚度矩阵等的计算方式,将其应用到包容式节点的分析之中。通过实现等几何分析程序并对包容式节点曲面进行力学分析,与有限元方法仿真结果进行对比验证了该方法的有效性。并对不同厚度的包容式节点采用基于Reissner-Mindlin退化壳理论的等几何分析方法进行分析实验,发现在包容式节点厚径比较小时分析结果严重失真,而当包容式节点厚径比较大时则能取得良好的精度。目前所使用的包容式节点厚径比满足该方法的要求。
