定轴转动过程中珠子多体动力学研究

赵建策　李晨曦　齐景江　王耀浥　王珩　李文博

摘 要：为了研究在定轴转动过程中珠子的动力学运动规律，本文通过珠子的拉格朗日学方程，建立了珠子的一般运动学方程。基于珠子的运动学方程提出了修正摩擦力并从能量角度出發分析了珠子的角速度随角度的变化情况，同时分析了不同摩擦系数条件下珠子角速度与平衡位置的变化。本试验设计了一套能够满足要求的装置，结合试验数据与理论公式分析了二者的符合程度。结论表明：通过多组试验数据拟合，珠子的运动平衡情况基本与理论一致，珠子的角速度运动方程与试验数据基本吻合。摩擦系数的改变能够在较小范围内引起角速度数值的变化，而珠子的平衡位置与摩擦系数的大小基本无关。

关键词：多体动力学;定轴转动;拉格朗日方程

中图分类号：O41     文献标志码：A     文章编号：1003-5168（2022）1-0033-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.01.007

Study on Multi-Body Dynamics of Beads Based on Fixed Axis Rotation

ZHAO Jianze1 LI Chenxi2 QI Jingjiang1 WANG Yaoyi1 WANG Heng1 LI Wenbo1

（1. Shenyang University of Aeronautics and Astronautics， Shenyang 110136，China; 2. Beijing Normal University， Beijing 100875，China）

Abstract： In order to study the kinetic motion of the bead during the rotation of the fixed axis， the general kinematic equations of the bead are established by the Lagrangian equations of the bead. A modified friction force is proposed based on the kinematic equation of the bead and the variation of the angular velocity of the bead with the angle is analyzed from the energy point of view. The variation of the angular velocity of the bead with the equilibrium position under different conditions of friction coefficient is also analyzed. The experiment is designed to meet the requirements of a set of devices， combined with the experimental data and theoretical equations to analyze the degree of compliance between the two. The conclusion shows that the equilibrium of the beads' motion is basically consistent with the theory through the fitting of several sets of experimental data， and the equation of motion of the angular velocity of the beads is basically consistent with the experimental data. The change of friction coefficient can change the value of angular velocity in a small range， and the equilibrium position of the beads is independent of the friction coefficient.

Keywords： multi-body dynamics; fixed-axis rotation; lagrangian equation

0 引言

多体动力学是力学问题的一个重要分支。在各个领域都有较为深入的研究。近年来，人们对于多体运动学的研究更为深入。其中在多体运动学领域对于“珠子动力学”的研究引发专家关注。“珠子动力学”的工作原理为：将一珠子放入圆槽中，圆槽以恒定的角速度运转。珠子通过与圆槽之间相互作用，从而沿着圆槽弧线向上/向下运动。Shovan Dutta[1]通过应用泰勒公式展开对珠子运动学模型进行分析。Ryn Seng，Michael Meeks[2]以理论力学角度深入分析了珠子的整个受力情况，进而给出了珠子运动模型的解释。Lisandro A Raviola， Maximiliano E Véliz[3]设计了一个可以合理测量珠子运动高度的装置，并合理分析了凹槽轮廓对于珠子的滚动约束影响并比较了角速度的差值。

首先建立了珠子的拉格朗日方程并得到珠子的稳定曲线，然后基于能量学方程建立了珠子的运动学方程，并提出了摩擦力修正项。研究在不同摩擦系数条情况下珠子的运动平衡情况变化。同时设计一套试验装置，分析了试验数据与理论的贴合程度，进而验证结论。

1 理论模型

1.1 珠子平衡模型

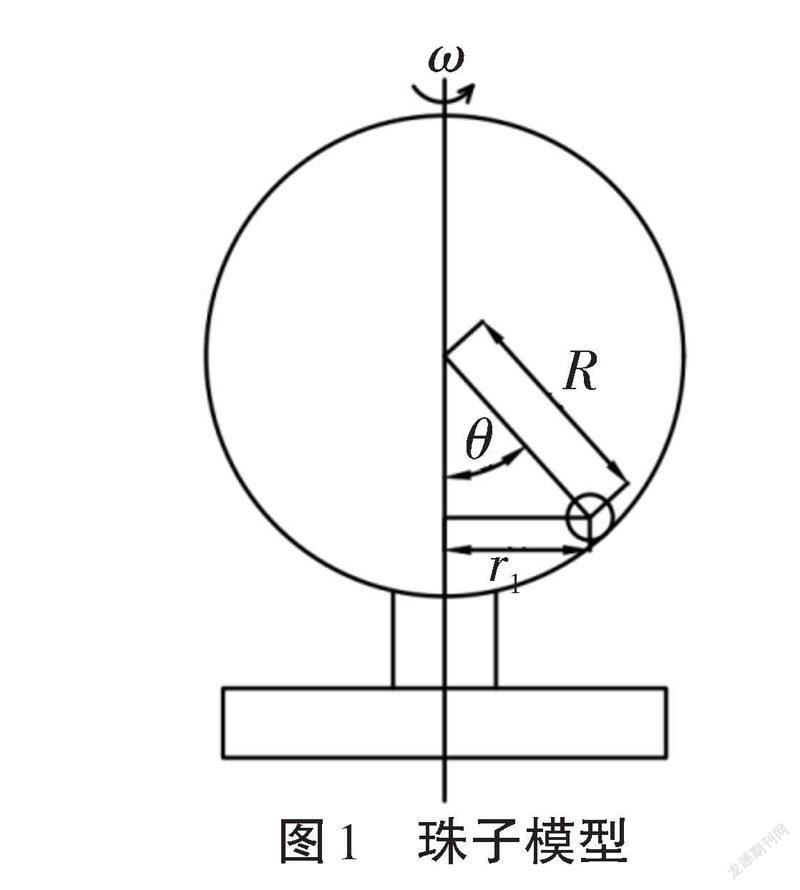
将一个质量为m、直径为d的小球放入半径为R的圆环内，圆环可以绕竖直轴以一定角速度ω旋转（见图1）。由于小球受到圆环的作用从而产生运动，在运动过程中的任意时刻，小球的高度距离底面高度为h，夹角为θ，则在上升过程中，珠子的动能Ek与势能Ep公式为

因此，拉格朗日方程表达式为

由拉格朗日定义可知，

无摩擦条件下珠子的运动的一般方程为

由于实际过程中存在不可避免的摩擦力影响，加入摩擦力修正项[μθm]，

求解最终解得，

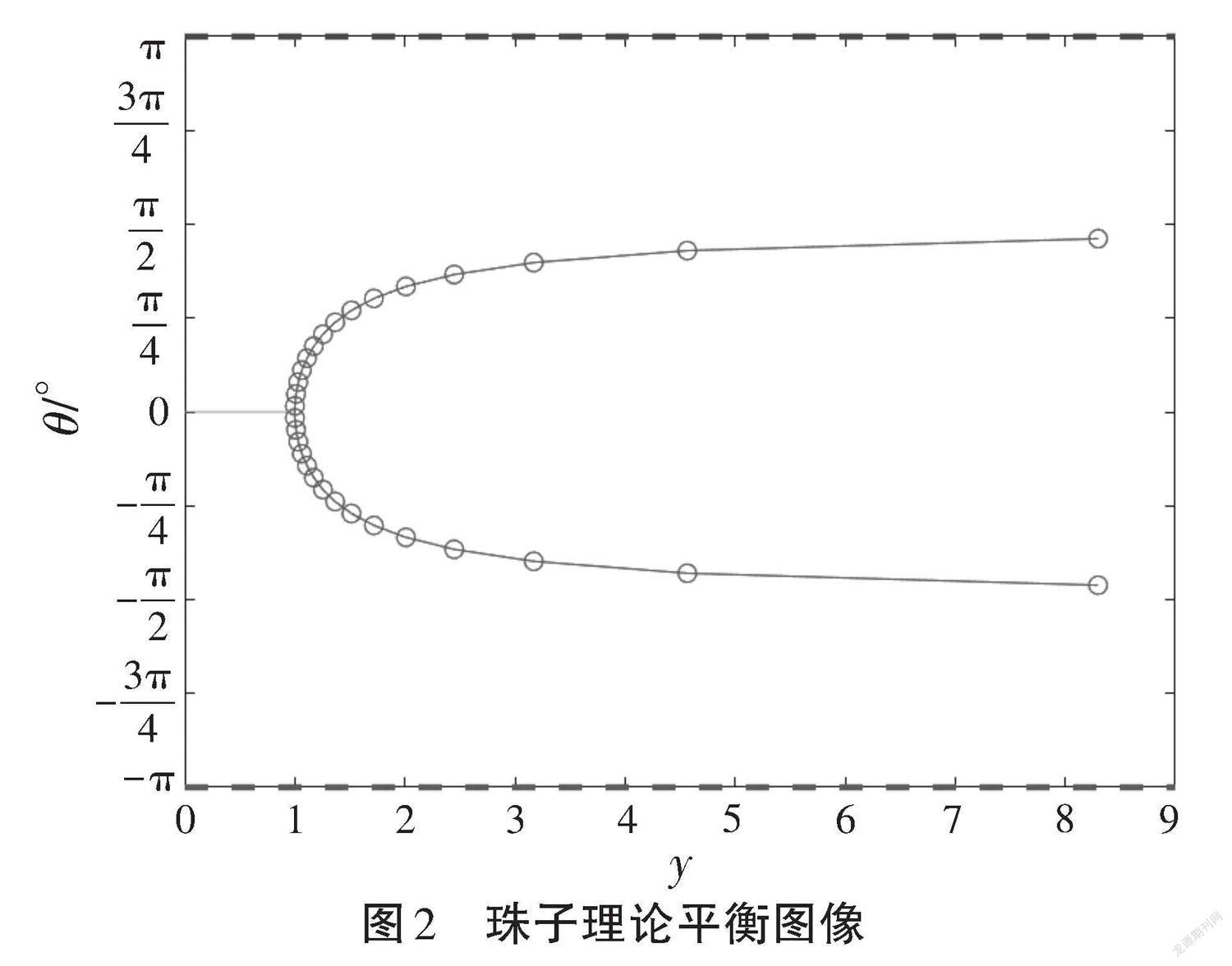
应用MATLAB绘制珠子平衡位置的理论图像如图2所示。

1.2 珠子角速度运动模型

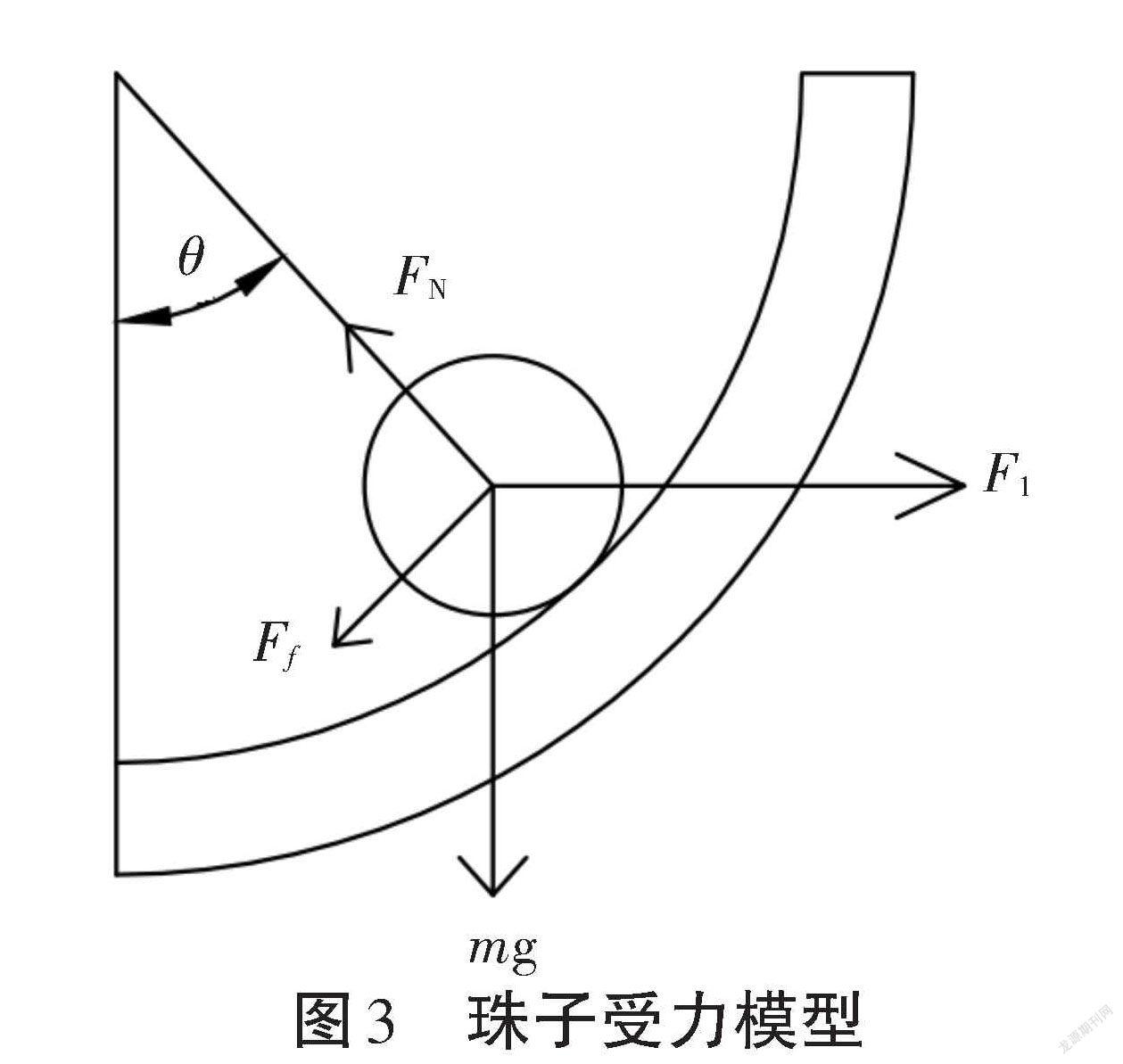
在实际过程中，珠子自身的滚动动能部分由于较小，基本可以忽略不计。为了更好描述模型，珠子的整体受力情况[4]示意图如图3所示。

依据珠子的受力模型，珠子在上升的运动过程中，计算珠子做功的表达式为

式中：ω1为小球角速度，F1为离心力，Ff为滑动摩擦，r为珠子的半径。其中，离心力F1与摩擦力Ff表达式为

将圆环与珠子作为一个系统，根据点的合成运动，珠子的绝对速度等于相对速度加上牵连速度矢量和。

va是绝对速度，也是钢球相对于静参考系运动的速度，其大小和方向都未知;ve是牵连速度，是圆环上与钢球重合的那一点相对于静参考系的运动速度;vr是牵连速度是珠子瞬时动系上与动点相重合之点的速度。牵连速度ve与相对速度vr表达式为

将（10）式代入（9）式矢量加和最终可得绝对速度的公式为

代入（7）式最终求得小球角速度的表达式为：

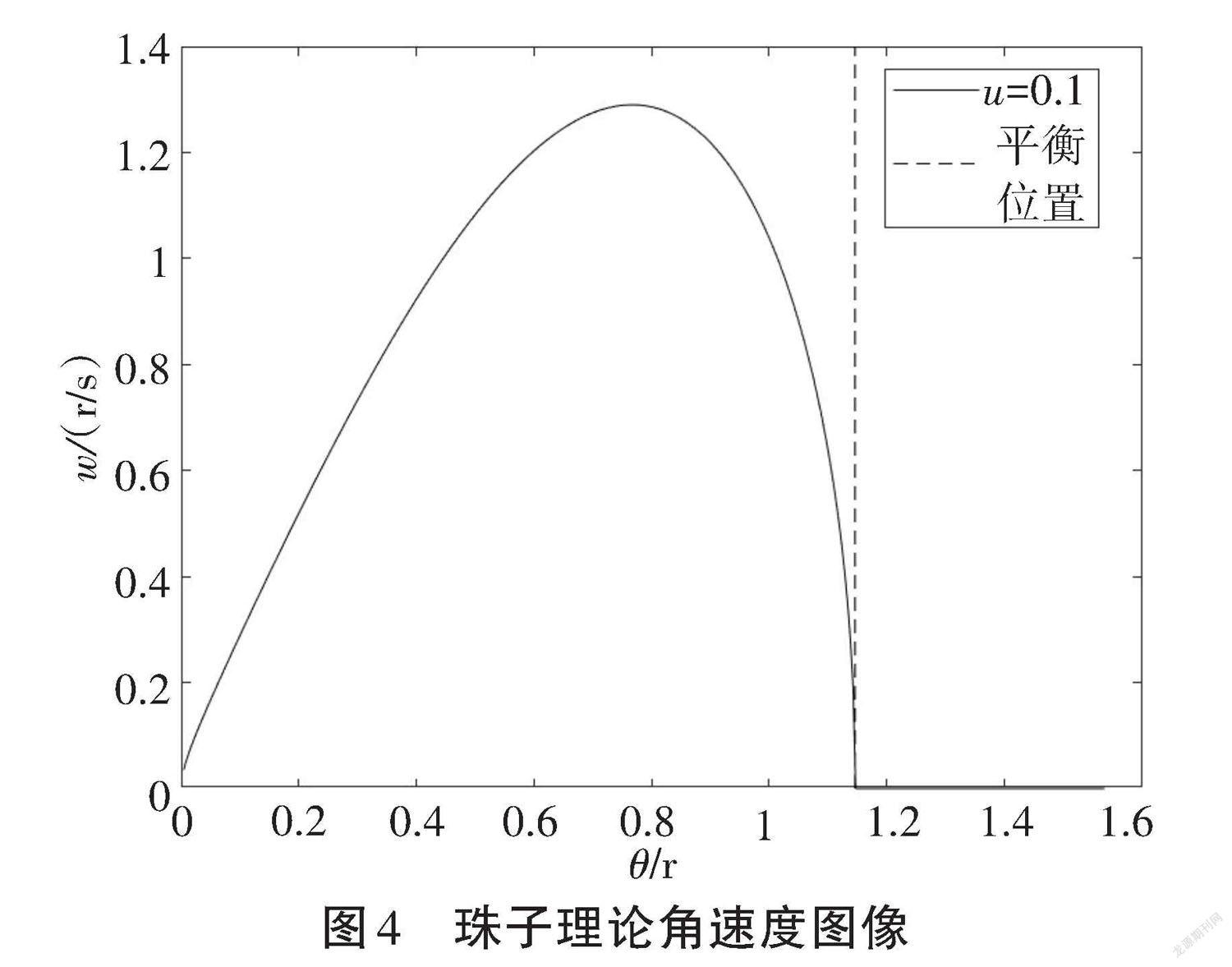
理论曲线为在圆环角速度为3.0 r/s条件下进行，曲线中珠子的角速度先随着角度增加而增大，然后随着角度增加角速度减小。在垂线处为珠子的平衡位置点。理论曲线基本验证了珠子角速度与珠子上升高度关系，同时在角速度与角度的图像上能够找到珠子的运动平衡点。由于平衡情况，珠子是相对圆环静止的，珠子相对于圆环速度为0。珠子的相对速度等效珠子的角速度。因此，珠子角速度为0的点即珠子运动平衡位置。图4进一步解释公式（1）忽略珠子角速度动能的原因，由于珠子的转动动能远小于珠子的动能，因而可以忽略。公式（12）（13）为珠子的角速度运动学模型理论，珠子的角速度变化与摩擦力、转过角度以及环半径有关。

本节内容主要建立珠子的平衡方程以及珠子的角速度运动学模型，并通过MATLAB软件绘制图像分析珠子的运动情况。

2 试验设计与操作

2.1 试验仪器设计

将质量约为10 g的小球放入圆槽半径为250 mm的圆环，通过步进电机驱动。步进电机由伺服控制器控制，角速度由步进电机调速器调整[6～8]。试验设备具体如图5所示。

为了满足试验过程的参数需要，针对需要物理量如數值、材质等进行相关参数说明，如表1、表2所示。

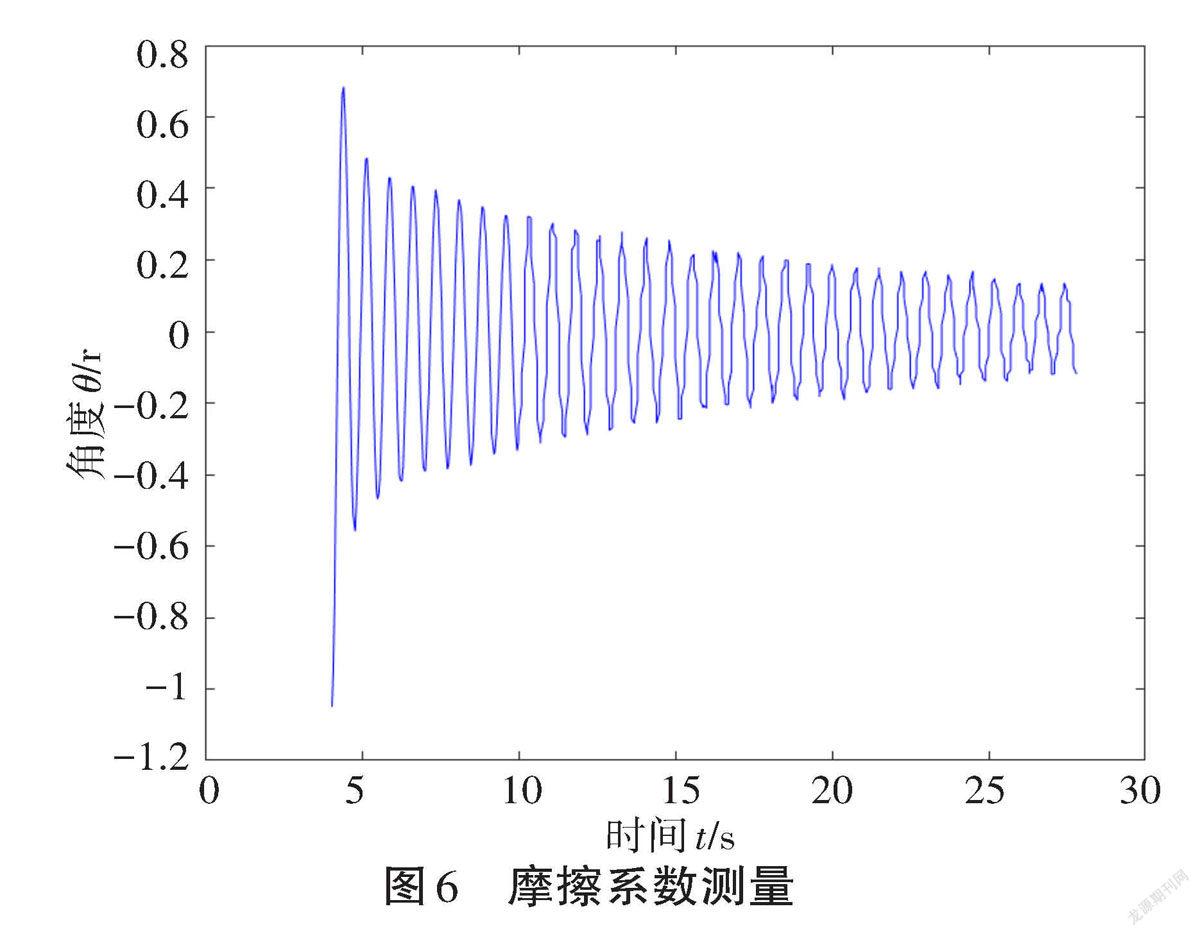
将珠子放在一定高度无初速度释放，通过摄像头拍摄视频，帧率为35帧。测量珠子与轨道之间的滑动摩擦系数，测量过程中无外界干扰保证滑动摩擦系数测量过程中的稳定性与准确性。摩擦系数测量结果如图6所示。

阻尼正弦波（Damped Sine Wave）是振幅会随时间增长而趋向零的正弦波函数。珠子由一定高度自由释放随时间变化，最终振幅趋于0符合阻尼正弦波。因此，拟合应用阻尼正弦波计算珠子的阻尼系数。珠子最终摩擦系数为0.08～0.30。

至此，为了实现研究的目标，珠子相关参数与物理量基本设计完成。

2.2 试验测量

在文献[1]中为了测量珠子的平衡高度，通过摄像头拍摄试验视频，帧数为30。但针对于文献[1]摄像头在上方，采取俯视图读数不利于角度的读取，在读数上误差较大。本试验设计思路与文献[3]类似，采取正视图读取数据，这样能够避免人为读数误差，且更加直观。进行多次试验减小误差并应用tracker软件对试验视频进行数据处理。通过tracker软件对试验过程中珠子进行定标处理。

通过多组试验进行平衡数据采集，同时试验过程排除外界因素干扰。理论曲线与实际曲线变化趋势基本符合（见图7），但在一定程度上减小了误差。试验过程中由于受拍摄视频帧数的误差影响，模型较为精确，基本验证了公式（5）（6）。

通过公式（12）（13）改变摩擦系数研究对于珠子的角速度、珠子平衡位置的影响，如图8所示。结果表明，对于珠子的角速度产生了较小的变化，且对于珠子的平衡位置几乎没有影响。

3 结论

研究定轴转动过程中珠子的动力学运动规律，建立了珠子的平衡方程以及角速度方程。同时，对于平衡方程提出了摩擦力修正项。从珠子的拉格朗日学方程分析了珠子的平衡变化趋势。应用阻尼正弦波拟合计算无初速度在一定高度释放的摩擦系数。基于能量方程分析了珠子角速度的变化。结合多组试验数据分析，珠子的运动平衡情况基本与理论一致，珠子的角速度运动方程与试验数据基本吻合。同时，分析了不同摩擦系数与平衡位置的关系，摩擦系数的改变能够在较小范围内改变角速度的数值，珠子的平衡位置与摩擦系数无关。

参考文献：

[1] DUTTA S，RAY S. Bead on a rotating circular hoop： a simple yet feature-rich dynamical system[J]. physics， 2011.

[2] SENG R，MEEKS M. A Bead on a Rotating hoop.ResearchGate：Find and share research[Z].2008.

[3]LISANDRO A R， MAXIMILIANO E V，HORACIO D S. The bead on a rotating hoop revisited： an unexpected resonance[J].IOPscience， 2017.

[4] 哈尔滨工业大学理论力学教研室.理论力学（I）[M].8版.北京：高等教育出版社，2016.

[5] 王燕玲.多体动力学在机械工程领域的应用[J].江西电力职业技术学院学，2021，34（1）：12-14.

[6] 李华柏，谢永超，胡扬.双馈风力发电系统中变桨距线性自抗扰控制系统研究[J].河南科学，2021，39（2）：190-195.

[7] 温国伟.多体运动学在机械工程领域的应用分析[J].科技视界，2017（13）：89.

[8] 李道力，于珈懿，高粼泽，等.多体动力学在机械工程领域的应用[J].湖北农机化，2019（12）：33.

收稿日期：2021-11-05

基金项目：国家自然基金项目“基于消除光栅衰减的高性能光致聚合全息存储材料研究”（No.11604223）;辽宁省教育厅科研项目“适于体全息存储的新型光致聚合物材料研制及其光动力学研究”（No.JYT19047）;辽宁省自然科学基金项目“高性能光致聚合信息存储材料应用研究”（No.2019-ZD-0222）;国家级大学生创新创业训练计划项目“基于Ansys有限元分析无人机结构设计与分析”（No.202110143007）。

作者简介：赵建策（2002—），男，本科生，研究方向：飞行器设计。

通信作者：王珩（1982—），男，博士，副教授，研究方向：材料。

3226500338272