基于手性超结构设计的可变形机翼研究进展
2022-03-11刘凯曹晓飞李营方岱宁
刘凯 曹晓飞 李营 方岱宁
摘要:安全、稳定、高效是当前飞机机翼设计领域重点关注的问题。机翼是提供升力的主要部件之一,可变形机翼在改善飞机整体性能方面有巨大潜力。以智能材料为代表的新材料的发展对机翼柔性蒙皮、驱动装置、控制技术以及轻量化结构产生了革命性的变革,拓展了手性拓扑结构的应用范围。基于手性拓扑结构、飞机机翼的气动性能分析、先进的制备工艺等技术而设计的变形机翼,可在不同飞行速度、飞行坡度以及周围流场改变其机翼形状,从而提高飞行效率,这是飞机机翼结构设计的前沿领域,也是未来重要的发展方向。本文介绍了手性超结构的设计方法及当前的研究现状,总结阐述了当前国内外基于手性拓扑结构设计的可变形机翼的研究进展,为我国可变形飞机机翼的设计提供参考。
关键词:变形机翼;柔性材料;手性拓扑结构;气动性能;飞行效率
中图分类号:224.3文献标识码:ADOI:10.19452/j.issn1007-5453.2022.01.003
基金项目:国家自然科学基金(11802030)
基于飞行工况进行机翼表面的主动形状控制是飞机工程中最具挑战性的问题之一。根据飞行高度、马赫数以及飞机重量(质量)进行机翼外形设计,并对其外形参数进行优化是常用的机翼设计方法,这种设计方案形成的机翼具有固定的几何形状[1]。固定构型机翼可以保证飞行器在一种特定工况下性能达到最优。然而,随着军民领域复杂任务需求的增加,飞行器面临空中侦察、抢险救灾、远程运输、航空摄影等日益复杂多变的飞行环境,如在飞行时旋翼和机身会产生严重的气动干扰现象,且该现象与飞行速度密切相关。因此,起降、巡航、高速飞行工况下对飞机机翼的外形参数均有不同的要求[2-3]。传统固定构型的飞机机翼不能改变其机翼外形以适应不同的飞行工况,导致飞行器性能的损耗[4]。自飞机诞生以来,研究者们试图利用仿生学的方法设计出能够自主变化的机翼,以提高飞行效率。力学、材料、制造工艺以及控制技术等学科的快速发展为解决此类问题提供了技术基础。
美国于1995年开展智能翼项目研究,截至今日,美国洛克希德-马丁公司(Lockheed Martin Corporation)、新一代航空公司(NextGen Aeronautics)、波音公司(Boeing)、德国航空航天研究院(DLR)对陆续原有结构进行改进,分别提出折叠翼[5]、变后掠翼(MFX-1)[6]、展向自适应机翼[7]、MFC驱动机翼[8]等机翼形式,实现了飞行器性能和效率的大幅提升。基于新材料、新构型的智能变形机翼的研究已然迈入快速发展阶段。
手性拓扑结构是由圆环节点和韧带连接而组成的一种新型轻质多孔结构,通过圆环节点的旋转和韧带的弯曲变形可实现整体结构的变形,可满足变形机翼轻量化、大变形、變形连续等需求。以北京理工大学、佐治亚理工学院等为代表的国内外高校对手性结构的动静态力学性能表征、变形机理、结构创新及理论研究进行了大量研究。目前,基于手性结构设计的变形机翼的大多数研究还处在从概念设计到试验表征的过渡阶段,尚未投入大规模使用。
变形机翼涵盖的范围较广,涉及的材料、构型种类众多。本文着重研究了基于手性结构设计的变形机翼的研究现状,综合目前材料、力学、控制技术等领域的发展现状,探究未来变形机翼的发展趋势。
1发展现状
1.1手性超结构
手性超结构由Kelvin于1894年提出。“手性”一词最初用来描述物理几何的关系,它的表述为:如果一个物体不可以由它的镜像通过旋转和平移得到,那么就称其为手性[9]。
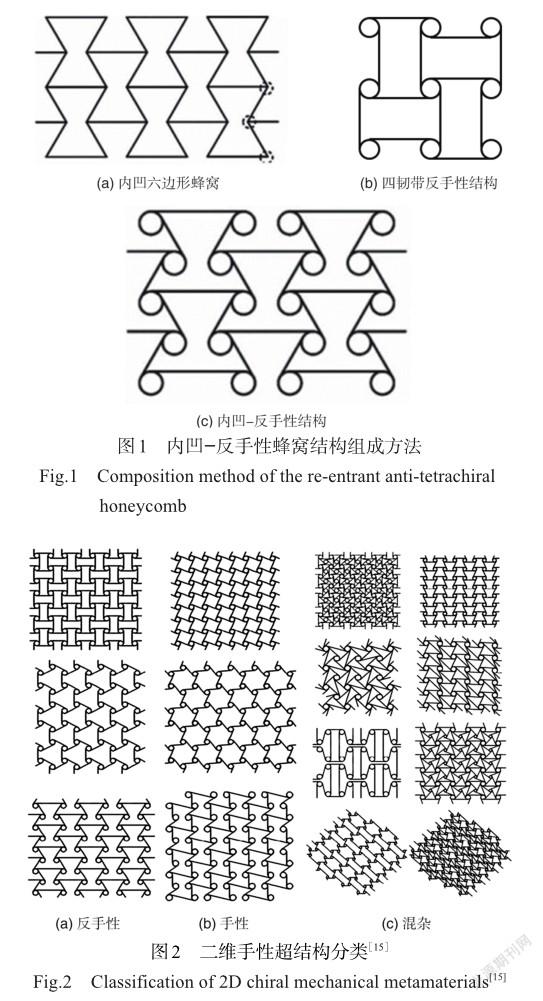
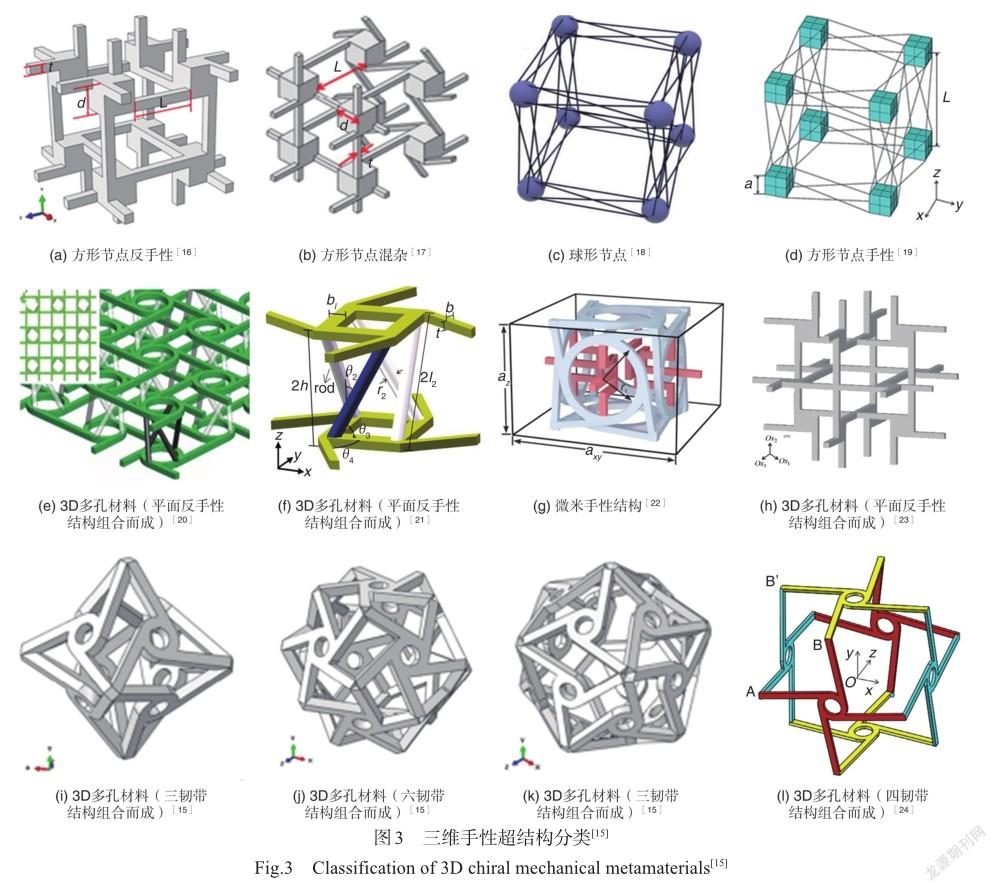
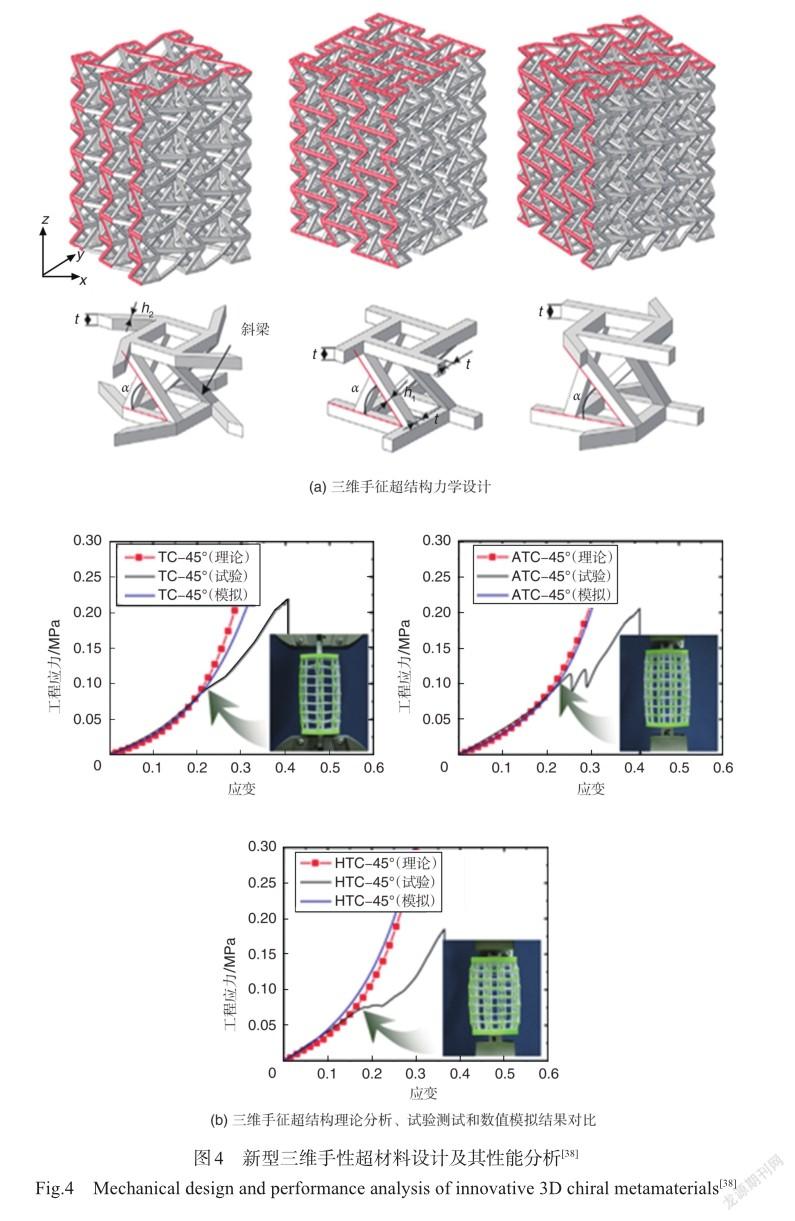
根据结构的特殊排列与空间维度,手性超结构可以分为二维手性结构和三维手性结构。二维手性结构是将节点和韧带在二维平面上进行周期性排列形成的平面结构,在实际的模型制备时需要将平面结构沿着面外方向拉伸一定厚度。三维手性结构是由节点和韧带在三维空间上按一定规则连接的三维结构。与二维平面结构相比,其构型更加复杂,种类更加丰富。根据圆环节点上连接的韧带数目,可以分为三、四、六韧带手性结构;根据韧带和圆环节点的相对位置又可分为手性和反手性。前人的研究表明,反手性结构受到压缩时韧带两端的圆环会朝不同方向旋转,使得韧带弯曲进而产生负泊松比效应。负泊松比结构不同于常规正六边形蜂窝结构,它在轴向压缩时,横向会收缩,整体结构瞬时密度增加,瞬时弹性模量增加,引起结构刚度增加,可提高结构的承载能力,这一结论被郭亚鑫等[10]研究中的内凹蜂窝结构与传统蜂窝结构的准静态力学试验证实。此外,负泊松比结构在承受面外载荷时胞壁易屈曲形成拱形,横向曲率和弯曲的主曲率一样,被称为同向曲率或双曲率现象,这种变形机制提高了面内切变模量和压陷阻力[11]。而常规的正六边形蜂窝在承受面外载荷时,会出现马鞍形状的反背曲率形变[12],以该形状作夹芯结构时会引起蒙皮的不连续变形[13]。魏路路等[14]将内凹六边形蜂窝顶点替换为圆形节点,并将相邻圆形节点采用反手性的连接方式得到内凹-反手性蜂窝,如图1所示。与传统蜂窝相比,内凹结构和圆环节点旋转的协同作用使得该结构的能量吸收性能更强,负泊松比效应更加明显[15-24]。因此,与传统蜂窝结构相比,具有负泊松比效应的手性结构在飞行器变形结构等应用中称为理想的结构材料。常见的二维、三维手性蜂窝结构分别如图2和图3所示。
1.1.1手性超结构理论研究
目前,关于手性超结构的理论研究多集中在探究手性蜂窝静态力学性能与解释负泊松比行为的机制上[25]。关于手性结构公式的推导多基于以下5个假设:(1)圆环节点是完全刚性的,即不考虑圆环节点的变形;(2)与施加载荷方向垂直的力忽略不计;(3)内力取决于观察到的结构的变形;(4)韧带的剪切变形与轴向变形忽略不计;(5)基于小变形假设,仅考虑韧带的弹性弯曲变形而忽略塑性变形。
基于上述假设,国外学者Prall等[26]根据能量法,由传统梁理论首次揭示了面内弹性模量、泊松比和结构参数的关系,并通过试验证明了六韧带手性蜂窝结构的泊松比为-1,该结果与理论模型吻合较好;Alderson等[27]认为上述方法没有考虑到韧带厚度与圆环重合的部分,提出了有效长度的概念,并推出了三、四韧带手性/反手性和六韧带手性蜂窝结构在小变形下的解析表达式。研究结果表明,在相同情况下,不同手性蜂窝结构在压缩变形时的力学性能有很大差异,其中,三韧带手性蜂窝结构的弹性模量最小;小变形情况下,四韧带手性蜂窝结构的泊松比等于-1。Lorato等[28]进一步研究了三、四、六手性蜂窝结构的面外力学性能和结构几何参数之间的关系,计算了不同手性蜂窝结构的切变模量以及横向剪切刚度的Voigt以及Reuss边界,研究结果对手性蜂窝结构的应用提供了理论指导。Bacigalupo等[29]基于微极弹性均质化和梯度均匀化方法探究了四、六韧带手性蜂窝结构的均匀化问题,通过弹性模量解析表达式揭示了名义应变与非对称应变在微极连续体的耦合关系。基于卡式定理,Mousanezhad等[30]系统推导了四、六韧带手性/反手性结构的弹性模量和泊松比的解析表达式。
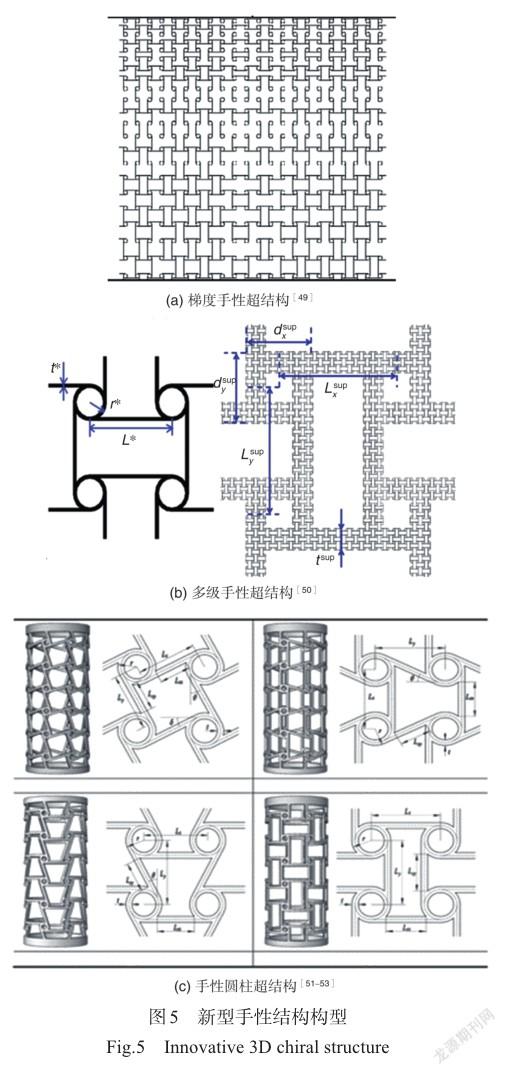
近年来,不仅仅国外学者展开了相关理论研究,国内学者在手性结构理论研究方面也取得了很大进展。针对现有的非中心对称的微极理论无法表征二维手性结构的手性效应问题,Liu等[31]提出一种连续介质理论模拟二维各向同性手性结构的手性效应,并基于此方法确定了手性蜂窝材料的有效材料常数。该离散模型的精确解验证了非手性模型无法预测的结果,很好地解释了拉胀-旋转以及剪切-旋转等效应。Chen等[32]基于均匀化理论探究了韧带长度不相等情况下的四边反手性蜂窝结构的各向异性性能特征,通过研究其弹性力学性能常数与几何参数之间的关系,得到了面内切变模量和泊松比封闭形式的表达式,该表达式对四边反手性蜂窝结构的各向异性设计具有指导意义。基于手性蜂窝结构的旋转机制,Fu等[21]将不同层的手性结构通过旋转的韧带连接设计出了三维手性结构,并基于梁理论和细观力学推导了弹性模量和泊松比的解析表达式。Yuan等[33]构造了一种广义的微极弹性均匀化方法来表征各向异性点阵中的方向模量、泊松比和耦合效应。研究结果表明,可以通过晶格结构的几何重构来调整结构的各向异性。在手性结构大变形的理论研究方面,Zhong等[34]基于梁的大变形弯曲理论,利用椭圆积分方法推导了手性蜂窝结构的面内非线性力学本构关系,揭示了其非正交各向异性的性质。Hu等[35-37]基于试验现象的观测先后建立了三韧带反手性蜂窝受不同方向压缩的理论模型,该模型能够很好地预测结构大变形时的泊松比变化和平台应力。如图4所示,Qi等[38]设计并通过理论、模拟和试验研究了新型三维手性超材料的力学性能。上述研究为手性结构用于可变形机翼提供理论基础。
1.1.2基于手性超结构的结构创新
随着生物医学、航空航天、智能制造等高端技术行业的不断发展,传统的蜂窝结构难以满足高比吸能、大范围泊松比可调可控以及轻量化等多种优良性能集于一体的多功能化需求,限制了行业和产业的发展。针对这一问题,一个较好的思路是通过创新结构设计来满足多功能一体化需求。因此,国内外学者在结构创新方面做了大量工作。Alderson等[39]通过将传统蜂窝结构中杆/板件角点替换为圆形节点设计了三韧带手性/反手性以及内凹三韧带手性/反手性结构。Lakes[40]基于将负热膨胀材料与手性结构相结合的思想,设计并研究了具有负热膨胀系数的手性超结构的力学性质。Ha等[19]将三维手性结构设计成具有拉扭耦合特性的立方体结构,并通过经典Cosserat弹性理论建立了该模型的本构关系。研究结果表明,该结构的泊松比具有明显的尺寸效应。随后,Ha等[41]还通过有限元分析进一步研究了三维各向同性手性结构的力学特性。除了周期性的规则设计之外,不规则和无序的手性超结构的力学性能也被学者们广泛研究。Mizzi等[42-43]基于传统六韧带手性蜂窝结构提出了非周期性对称的六韧带手性蜂窝结构以及节点无序结构,实现了更大范围的负泊松比调控,拓宽了手性蜂窝结构的应用场景。Pozniak等[44]探究了圆形节点大小随机分布的反手性结构的负泊松比效应。
国内学者在结构创新方面也做了大量工作。Fu等[21]通过斜向扭转韧带将不同平面的二维手性结构连接,形成了平面内外均可扭转的新型三维多孔材料。Chen等[32]设计了韧带长度不等的四韧带反手性蜂窝结构。Duan等[45]基于二维手性材料的拉扭耦合效应提出三维负泊松比材料设计方法,实现了泊松比和弹性模量在更大范围的调控。Zhao等[46]设计并探究了四韌带和六韧带结构的形状记忆效应,研究结果表明手性超结构在开发可编程超材料等方面具有很大的潜力。传统的优化方法通常是改变圆环节点的形状、韧带和圆环节点的连接方式等,与基于优化算法的优化方法相比,存在用时时间长、鲁棒性差、可解释性不强、性能不能达到最优等缺点。近年来,拓扑优化、机器学习等优化算法为力学超材料在承受不同载荷下的优化设计提供了可行的技术支持。大连理工大学张会凯[47]基于独立节点密度法、多材料模型和渐进均匀化理论设计的双材料多孔负泊松比超材料比单一材料的承载能力、抗剪切能力更强。基于遗传算法,Qiu等[48]对六韧带手性蜂窝结构的形状和尺寸进行优化,使得优化后的结构在大变形时弹性模量和泊松比保持在一定的范围内,该结构的设计方法对飞机变形的设计具有重要意义。如图5所示,北京理工大学的方岱宁课题组也开展了大量研究工作,并设计了梯度手性超结构[49]、多级手性超结构[50]和混合手性圆柱超结构[51-53]等创新构型,揭示了手性超结构用于可变形机翼的内在机制和变形机理。
1.2变形机翼
机翼是提供升力的主要部件,其面内设计参数主要包括展长、弦长、后掠角;面外设计参数主要包括扭转刚度、翘曲度、弯度等[54],这些结构参数与决定飞行器飞行状态的升力系数、升阻比、外倾角等参数密切相关。变形机翼(morphing wings)也可称为智能机翼(smart wings)、主动机翼(active wings)或自适应机翼(adaptive wings),能够根据实际的飞行环境改变其外形参数,进而减少或消除颤振,减小气动阻力,改善操纵特性,使得飞机在飞行任务中始终处于最优状态[55-56]。此外,该机翼还可以扩展飞行器的飞行包线,减少襟翼式结构[57]。欧美等发达国家对变形机翼的研究起步较早,变形机翼的设计最早可追溯至1890年,Clement Ader基于蝙蝠外形而设计出具有可折叠翼的飞行器,并将其命名为“Eolo”,如图6所示。但由于该设计只是简单的模仿而缺乏一定的科学依据,最终以失败告终。直至1903年,Wright兄弟设计出Wright Flyer I”并试飞成功,实现了人类的飞行梦想。此后30年间,欧美等国家先后开发出变后掠翼、伸缩翼、变展长、变弦长、变弯度等可变形机翼。自20世纪40年代开始,关于变形机翼的研究进入快速发展时期,如意大利、德国的Tornado、美国的X-5、F-111、XB-70,苏联的MAK-10、SU-17、MIG-23、TU-160等变体飞行器为该时期的典型代表[55]。由于早期的机械制造工艺、材料研究水平较低,飞行器结构设计往往比较复杂,机身只能采用刚度更大的材料,以满足更高承载性和更快的飞行速度需求。机翼变形主要通过传统机械式的刚性结构之间的滑动和转动来实现。这种机翼结构需要多个铰链和轴承的协同作用,虽然可以在一定程度上改善飞机性能,但驱动装置、变体结构的使用,一方面对制造工艺、控制精度要求较高;另一方面增加了飞机结构的复杂程度,维护成本高,同时增加了飞机的重量(质量),限制了飞机的机动性、灵活性以及可操作性,无法满足未来军民领域对飞行器轻量化、智能化、信息化等多功能一体化的需求,因此无法广泛适用飞行器结构。表1列举了自1890年至20世纪80年代研发的部分变形机翼的型号与及其变形方式。经过近百年的发展,研究者基于变体结构设计了多种变体机翼。目前,关于变形机翼的分类有不同的标准,依据机翼的变形模式,本文将其主要类型大致分为伸缩翼、折叠翼、变后掠翼以及倾转旋翼4种类型,结构示意图如图7所示。
在航空航天领域,变形机翼最重要的功能是为机翼提供连续变形的能力。新型变形机翼的研发已成为各国航空工业的重要任务之一。20世纪80年代以来,柔性材料的研究为解决飞行器高承载性和高机动性之间的矛盾提供了新的方案。同时,计算机仿真技术的发展极大地缩短了从设计到验证所需的时间,力学体系的完善为机翼的可靠性验证提供了理论指导。各国的研究者们从材料研究、制造工艺、结构创新、控制技术4个方面相继提出不同构型、不同材料的变形机翼。


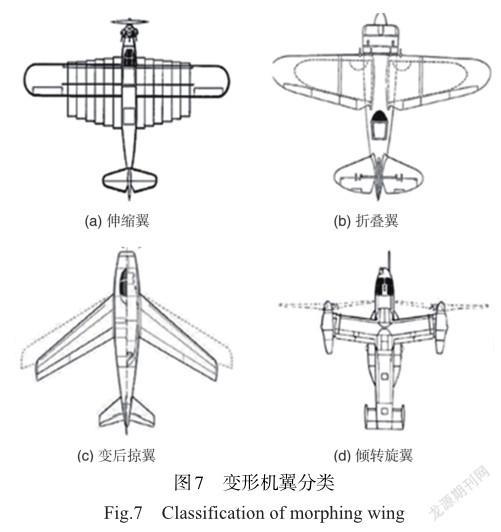
本文将变形机翼的发展历程分为刚性变形阶段和柔性变形阶段。第一阶段为1890年至20世纪80年代,这一阶段机翼的材料主要为传统的刚性材料,变形模式以刚性变形为主;第二阶段为20世纪80年代后,这一阶段的材料主要为柔性材料,变形模式以柔性变形为主。本文主要介绍柔性变形阶段的机翼发展历程。
1.2.1基于手性结构设计的变形机翼
近年来,在结构优化设计和材料选择方面,多孔材料因其具有良好的比刚度、比强度以及吸能特性而得到广泛关注。自然界中存在大量的多孔材料,如木材、蛋壳、蜂窝等,如图8所示。根据构型排布特点,多孔材料可以分为两大类:一类是泡沫材料/结构,其典型特征是构型无序,进一步地根据其内部结构的连通性可以分为开孔泡沫和闭孔泡沫;另一类是构型有序,排列呈周期性分布的多孔结构,其内部结构尺寸较为均匀,也称为点阵结构。比较常见的点阵结构包括蜂窝结构、格栅结构、杆状点阵结构等。手性蜂窝是一种有序的多孔结构/材料,与传统的多孔材料相比,它具有丰富的变形模式、较高的可设计性以及多样的设计参数。
由于传统机翼结构的灵活性较差,基于仿生学思想,从结构设计的角度出发,1999年德国航空航天研究院(DLR)提出“手指概念”,其核心是一种由分离的板状元件构成的柔性机翼,元件之间通过旋转接头连接而成。与传统机翼结构相比,该机翼呈连续变化的弧度的外表面可为飞行器提供更好的升力和更小的阻力[58]。随后,该研究机构针对机翼结构中梁、肋、桁条等零部件高度分化带来的结构复杂、维修成本过高的问题,提出了皮带-肋的自适应机翼的概念,这种设计方法是使用新的belt rib将原有零部件高度集中[59]。相比于传统刚性变形翼形结构,这种设计方法的主要优势在于:(1)零件大幅减少,维修成本低,质量轻;(2)承载能力强,强度大,可靠性高;(3)自主变形,无须借助主动驱动系统;(4)翼型产生连续变形,可控制机翼和叶片的气动弹性和结构性能。

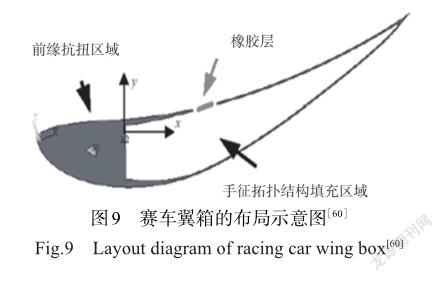
上述研究结果表明,连续变化弧度的外表面可提升飞行器性能。手性蜂窝的变形机制能够很好地产生连续变形。手性蜂窝结构由圆环和韧带组成,在变形过程中韧带绕圆环节点旋转,这种旋转机制允许翼型截面在平面内产生连续的变形。受到上述研究的启发,众多学者开始思考将具有负泊松比特性的手性蜂窝结构用于变形机翼,以探究新结构对机翼性能的影响。然而,传统制造工艺存在周期长、成本高、易产生缺陷等问题,难以发挥手性结构的优势,极大地限制了手性蜂窝结构的工程应用。近年来,增材制造工艺以及计算机数值仿真技术的不断发展解决了上述问题。2005年,谢菲尔德大学Bornengo等[60]以赛车车型Eppler 420为研究对象,首次将六边形手性蜂窝结构作为赛车翼箱的芯层结构(见图9)。2006年,佐治亚理工学院Spadoni等[61-62]研究了动态载荷下手性结构的频响特性,采用动态形状函数描述手性结构在宽频率范围内的变形行为。数值仿真结果与模态试验表明,手性拓扑结构在固有频率激励时具有局部的形变特征,由此可利用共振效应来最小化局部变形出现所需的功率。基于前述研究,Spadoni等[63]随后将手性结构应用于机翼结构,并通过计算力学和结构分析的物理耦合模型研究了手性拓扑结构对机翼气动性能的影响,基于手性拓扑结构设计的机翼及试验装置如图10所示。2008年,布里斯托大学Martin等[64]探讨了基于手性蜂窝结构设计的被动变形机翼的弧度随气流的变化,试验结果表明,机翼的变形与气动载荷之间呈现非线性关系,通过调整手性蜂窝结构参数可改變机翼的外倾角,从而提供较高的变形能力,同时能保持机翼翼盒的结构完整性。2011年,韩国学者Heo等[65]以铝合金为基体材料,基于手性蜂窝、六边形蜂窝以及内凹六边形蜂窝制备了三种不同类型的机翼结构(见图11),采用流固耦合模型模拟机翼在流场作用下的变形能力。数值结果表明,以负泊松比蜂窝结构为芯层的机翼能够兼顾刚度和柔性的需求,同时在相同的载荷时具有更低的局部应力。该研究表明,手性蜂窝结构具备用作被动翼型的潜力。2011年,代尔夫特理工大学Vos等[66]提出一种压力自适应蜂窝结构(见图12),该结构是利用蜂窝内的压力来自发改变其结构的刚度和形状,风洞试验表明压力自适应蜂窝可改变机翼部分的空气动力学特性,基于压力自适应蜂窝设计的变形机翼如图13所示。赵显伟[67]通过拉伸试验和面外承载试验证明手性蜂窝结构具有面内变形、面外承载的双重作用,并将三、四、六韧带手性/反手性蜂窝结构材料作为飞机机翼的填充材料,通过改变手性蜂窝结构参数可得到不同厚度的机翼蒙皮,气动载荷试验结果进一步表明手性蜂窝结构可满足面内低模量和面外高承载需求,它是作为机翼蒙皮合适的填充材料。填充材料为手性蜂窝结构的蒙皮试验装置如图14所示。
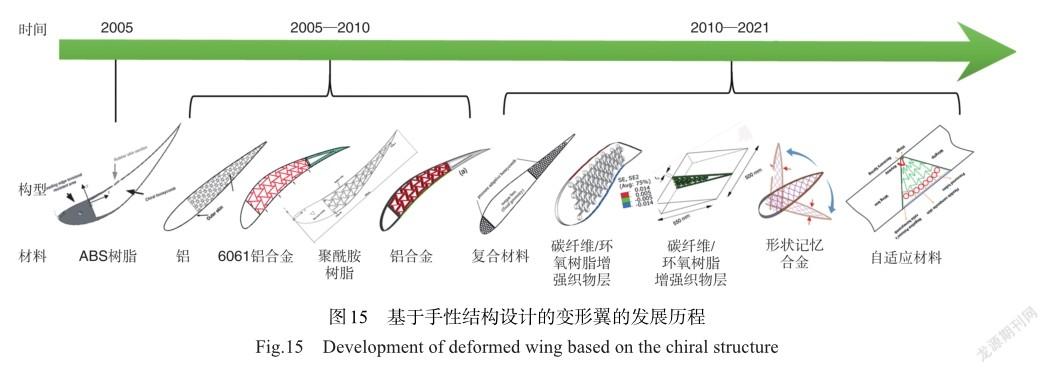
需要指出的是,由于需要同时满足高承载和高机动性的需求,早期受限于材料科学的限制,机翼采用的材料多为金属材料,这在一定程度上抵消了因结构设计带来性能提升的优势。因此,仅通过结构设计带来性能的提升有限。随着新材料的发展,研究者们开始将目标转向新型材料的应用。图15为近20年基于不同材料制备的手性结构机翼的发展历程。从时间历程可以看出,基体材料逐渐由树脂、金属铝转变为复合材料、智能材料和自适应材料。

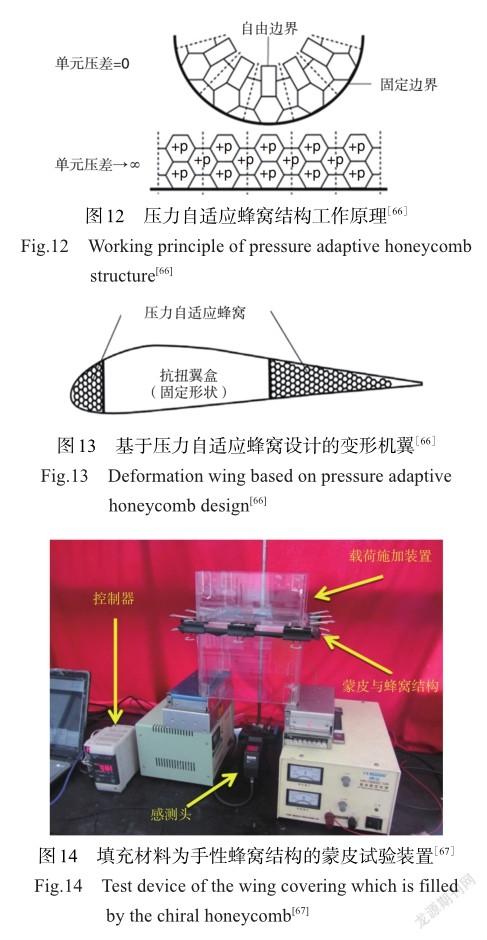
1.2.2基于新材料设计的变形机翼
智能材料是20世纪90年代发展起来的一类新型功能材料。与传统材料不同,智能材料通常以某一智能化体系方式存在,其定义为:由多种材料通过有机紧密复合或严格的科学组装而成的材料系统[68]。智能材料种类众多,其中,形状记忆合金、压电材料、形状记忆聚合物、电流变材料、磁流变材料均可归为智能材料[69]。在新材料中,复合材料常作为蜂窩结构的基体材料,形状记忆合金、形状记忆聚合物以及压电材料等智能材料通常作为驱动器来驱动机翼的变形。
(1)复合材料
复合材料是将不同性质的材料通过先进的制备工艺组合而成的新型材料,相比于传统的金属材料,复合材料具有热膨胀系数小、可设计性强、比刚度大、比强度大等特点,可满足轻量化、高承载等需求,已逐渐成为交通运输、航空航天领域关注的热点[70-73]。
2010年,米兰理工大学研究了基于长纤维增强聚合物制备的具有手性拓扑结构的复杂蜂窝结构在载荷作用下的变形模式和失效机理[57];之后,他们又提出了复合材料手性蜂窝结构用作机翼内部柔性结构的解决方案。具体方法是在复合材料制备工艺中,将不同的单元黏合,在黏合过程中将弹性嵌件均匀压在一起,由此产生的复合材料手性结构可以用非常薄的韧带和不同类型的复合材料制成。同时,他们也提出了复合波纹层合板用作外部柔性蒙皮的设计方法:将蜂窝结构支撑的弹性层集成到波纹层合板中,以解决波纹板不规则的表面会增加气动阻力并降低升力的问题[74]。基于复合材料制备的手性结构的机翼变形模式如图16所示。2012年,西班牙航空公司研究了碳纤维/环氧树脂增强复合材料的失效机理以及复合材料铺层顺序、手性结构几何尺寸对机翼静态和动态性能的影响[75]。结果表明,复合材料手性蜂窝芯用于气动表面结构在有限的应变范围内具有较大的弧度变化,并基于计算结果进行了数值优化。优化结果表明,在低速飞行模式下,升力曲线斜率增加一倍,在迎角范围内增大了升力系数。以上研究均表明基于复合材料制备的手性结构用于变形机翼具有巨大潜力。

(2)形状记忆合金
形状记忆合金(SMA)材料因其具有独特的形状记忆效应、超弹性特性以及生物相容性等优势,具有广泛的应用空间和多元化的发展前景[76-77]。
为探究形状记忆合金材料对手性蜂窝结构力学性能的影响,2008年,谢菲尔德大学Hassan等[78]提出智能蜂窝结构的概念,该结构以形状记忆合金为基体材料制备手性蜂窝结构,研究了该结构在准静态压缩下的泊松比变化历程,并进一步探究智能蜂窝结构用作可展开桁架的变形行为。2012年,布里斯托大学设计了一种基于形状记忆合金材料制备的天线,该天线由手性结构组成,具有可开展特性。模态分析表明该结构的模态响应的最小阈值满足设计需求。目前,变形飞行器朝着小型化和轻量化的方向发展,这限制了电池的尺寸和容量。因此,飞行器的飞行时间和航程有限。机翼的变形需要驱动器的驱动,得益于材料的形状记忆效应,基于形状记忆合金制备的智能驱动器具有能量密度大、输出位移/力高等优点。20世纪末至今,美国国防预先研究计划局(DARPA)、美国空军研究实验室(AFRL)、美国国家航空航天局(NASA)等均展开SMA应用于机翼的研究[79]。如美国国家航空航天局(NASA)和波音公司合作研发的一种由SMA驱动的可变弯度后缘襟翼[80],SMA驱动的可变翼梢小翼无人机PTERA[76],如图17所示。2014年,印度理工学院Prajapati等[81]将SMA驱动器嵌入手性蜂窝结构,为手性结构的变形提供能量。SMA驱动手性蜂窝结构变形如图18所示。
(3)形状记忆聚合物
形状记忆聚合物(SMP)是一种可实现大应变的高分子聚合物,由于温度变化会引起聚合物分子链的熔融结晶,因此会在聚合物中产生形状记忆效应。相比其他形状记忆材料,形状记忆聚合物具有形变大、温度转换易控以及成本低等优势[82-84]。

2014年,波士顿大学Rossiter等[85]利用热响应形状记忆聚合物(SMP)制备了六韧带手性结构,通过热循环试验使其表现出自展开功能,并进一步研究了韧带和圆环夹角对其变形性能和变刚度性能的影响。2017年,布里斯托大学Neville等[86]以剪纸技术Kirigami为设计灵感,使用SMP制备了具有可调变形和形状变形性能的六边形蜂窝结构。2018年,Huang等[87]将ABS塑料的内凹蜂窝结构用SMP的薄板相连接,由于SMP材料的形状记忆效应,该结构表现出形状记忆效应和变刚度特性,并通过试验进一步研究了薄板厚度、温度等对形状记忆效应和变刚度性能的影响。基于形状记忆聚合物制备的零泊松比蜂窝结构如图19所示。SMP也可用作驱动器,2021年Tao等[88]基于蜂窝结构的接触摩擦带电波状表面,设计了一种用于生物力学和无人机变形机翼能量收集的蜂窝式摩擦电纳米发电机,能够在飞行器飞行过程中收集机翼振动产生的动能并将其转化为电能。变形机翼发电机装置如图20所示。

(4)压电材料
压电材料是一种具有压电效应的多晶体,能够将机械能和电能相互转换,即材料尺寸的变化会产生电流,电流也会引起材料尺寸的变化。压电效应的特殊性质决定了基于压电材料的驱动器比传统的机械式以及液压式驱动器的响应速度更快、能量密度更大、结构更简单且更易于控制,因此,被广泛应用在结构振动、变形控制等方面[56-77]。因此,一般情况下,压电材料较少地用于手性蜂窝的基体材料,而是为驱动装置为结构的变形提供动力。
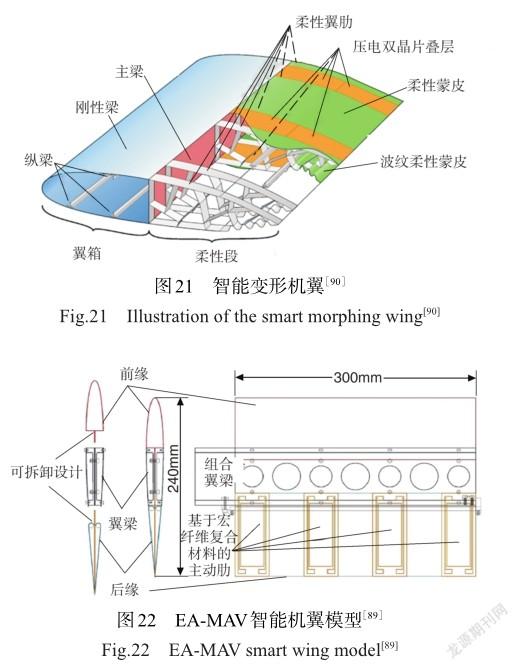
2011年,加拿大航空航天研究所Wickramasinghe等[89]提出以压电陶瓷纤维作为主驱动机构,电活性聚合物作为辅助驱动机构的双活性材料系统的智能变形机翼方案,如图21所示。具体方法是在双晶片驱动器外围覆盖一层预拉伸蒙皮,通过蒙皮的轴向压缩载荷进而使驱动器产生压电效应,最终发现这种设计方案可以提高机翼的变形能力。EA-MAV智能机翼模型如图22所示。2019年,普渡大学Henry等[90]在NACA 0012翼型的基础上进行改装,内部结构使用桁架结构进而引导外层蒙皮的变形,采用压电纤维复合材料(MFC)驱动器驱动整体结构的变形,并采用多学科优化技术对驱动方案以及蒙皮材料参数进行优化,最终使滚转力矩增加27.67%,飞行速度提升83.4%。2020年,俄亥俄州立大学Chillara等[91]提出一种由压电PVDF薄膜分层而成的双稳态层合板,将压电纤维复合材料、形状记忆合金嵌入其中,利用压电材料的压电效应可有效捕捉由结构形变引起的电荷变化,进而将其转化为电信号,可有效捕捉结构中的微小变形。
2当前研究面临的难点
早期的变形机翼多采用传统的机械或液压驱动,机翼材料多为金属材料,变形模式以刚性变形为主。近年来,随着形状记忆合金、压电材料、复合材料、电感材料、可自愈材料等智能材料的兴起,深度学习、强化学习、多传感器融合等智能控制技术的发展,增材制造、复合材料成形工艺等先进制造方法的应用,非线性动力学、流固耦合等仿真技术的完善,推动变形机翼完成了由刚性变形阶段到柔性变形阶段的转变。然而,基于手性结构设计的变形机翼的研究还存在以下几方面问题。
(1)材料性能存在缺陷
表2為几种基于智能材料制备的智能作动器的性能对比,从表中可以看出没有一种作动器能够同时满足响应速度快、能量密度高、输出位移大、输出力大、刚度大的需求。现代飞行器面临更加复杂的飞行任务,需要进一步研发新材料以解决现有智能作动器的缺陷,同时更好地平衡飞行器面临的高承载与高机动性之间的矛盾。
(2)结构设计较为单一
在手性超结构的胞元构型设计方面,主要研究对象仍以传统节点-韧带型手性结构为主,其韧带多是实心的杆或板,不能满足当前对结构设计轻量化、隔热、抗爆、抗冲击等多功能一体化的需求。目前,关于基于手性结构设计的变形机翼研究仅停留在二维层面,多数研究的结论仅是通过数值仿真得出的,缺乏试验验证。
(3)理论研究不够完善
目前,关于手性结构的力学性能研究主要集中在准静态面内力学和面外力学性能研究方面。在动态冲击变形方面,还缺乏手性结构的冲击吸能理论模型,有关实现结构的吸能效率和冲击吸能能力方面的提升还需深入研究。另外,很多复合材料、形状记忆合金以及形状记忆聚合物等材料还缺乏准确描述其力学行为的本构模型。
(4)控制技术不够全面
变形机翼的设计主要集中在结构设计以及材料选择上,局限于驱动性能的研究以及一些静态的分析,对于智能变形机翼的动态特性分析较少;非定常气动力、柔性结构等因素使得飞行器的动力学模型往往涉及非线性、高维度、多参数等问题,增大了仿真求解时间,数值模拟难以做到与实际情况同步。强非线性对变形机翼的主动控制和精确驱动提出了更高的控制技术需求,而目前关于控制技术的研究仍不够全面,仅仅处于起步阶段。

3结束语
基于手性结构设计的变形机翼大多还处于试验验证阶段,还未投入大规模量产。一方面,制造成形控制技术不够成熟,在制造过程中会出现不可预测的缺陷,影响飞行器的安全;另一方面,实际飞行环境远比试验环境复杂,从概念设计到试验验证需要足够的时间加以验证。
智能材料、增材制造以及人工智能等技术的发展推动了变形机翼由刚性变形到柔性变形的转变。近年来,变形机翼智能材料的本构理论及其可应用场景研究,增材制造成形缺陷理论及新成形工艺研究,机器学习、深度学习、强化学习等人工智能技术研究引起了广泛关注。随着增材制造工艺的发展与完善,变形机翼将很可能实现低成本、大尺寸、大规模和标准化生产。人工智能理论的发展将极大地推动多目标优化、拓扑优化等优化算法的求解效率。根据变形方式,本文将现有的变形机翼大致分为伸缩翼、折叠翼、变后掠翼和倾转旋翼4类。在未来,随着变形蒙皮、驱动装置、变形机构、控制技术的发展,机翼的变形方式将会朝着多种变形组合的方向发展,轻量化多孔材料由传统的设计到验证的设计方法将难以满足复杂动态多变的载荷需求。基于人工智能求解的优化方法将缩短结构优化时间,使得多孔材料能更好地满足载荷需求,实现材料、结构和分布驱动参数的最佳匹配。
参考文献
[1]Monner H,Sachau D,Breitbach E. Design aspects of the elastic trailing edge for an adaptive wing[R]. German Aerospace Center Braunschweig(Germany)Inst of Structural Mechanics,2000.
[2]靳鹏,樊枫.直升机机身干扰对旋翼气动与噪声特性影响研究[J].航空科学技术, 2021, 32(6): 9-20. Jin Peng, Fan Feng. Study on the interaction influence of helicopter fuselage on the rotor aerodynamics and aeroacoustics[J]. Aeronautical Science & Technology, 2021, 32(6): 9-20. (in Chinese)
[3]陈以金.变体飞行器柔性蒙皮及支撑结构性能研究[D].哈尔滨:哈尔滨工业大学, 2014. Chen Yijin. Study on flexible skin and supporting substructure ofmorphingaircraft[D].Harbin:HarbinInstituteof Technology, 2014. (in Chinese)
[4]孙杨,昌敏,白俊强.变形机翼飞行器发展综述[J].无人系统技术, 2021, 4(3) : 65-77. Sun Yang, Chang Min, Bai Junqiang. Review of morphing wing aircraft[J]. Unmanned Systems Technology, 2021, 4(3): 65-77. (in Chinese)
[5]Bye D,Mcclure P. Design of a morphing vehicle[C]// Proceedingsofthe48thAIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,2007.
[6]Flanagan J,Strutzenberg R,Myers R,et al. Development and flight testing of a morphing aircraft,the NextGen MFX-1[C]// Proceedingsofthe48thAIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,2007.
[7]Moholt M,Benafan O. Spanwise adaptive wing[C]//3rd Annual Convergent Aeronautics Solutions Showcase and Innovation Faire,2017.
[8]Monner H,Riemenschneider J,Opitz S,et al. Development of active twist rotors at the German Aerospace Center(DLR)[C]//Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference 19th AIAA/ASME/AHS Adaptive Structures Conference,2011.
[9]Thomson B K,Kelvin B,Thomson W. Baltimore lectures on molecular dynamics and the wave theory of light[D]. Cambridge:Cambridge University Press,2010.
[10]郭亚鑫,袁梦琦,钱新明,等.内凹型蜂窝结构在冲击载荷作用下的力学行为及响应特性研究[J].中国安全生产科学技术, 2019, 15(12): 5-10. Guo Yaxin, Yuan Mengqi, Qian Xinming, et al. Study on mechanical behavior and response characteristics of inner concave honeycomb structure under impact load[J]. Journal of Safety Science and Technology, 2019, 15(12): 5-10. (in Chinese)
[11]Caddock B D,Evans K E,Masters I G. Honeycomb cores with a negative Poisson’s ratio for use in composite sandwich panels[C]//Proceeding of the Eighth International Conference on Composite Materials,1991.
[12]Evans K E. The design of doubly curved sandwich panels with honeycomb cores[J]. Composite Structures,1991,17(2):95-111.
[13]邱克鵬,王智,王欢.手性性材料结构的等效力学性能分析计算[C]//第七届中国航空学会青年科技论坛, 2016. Qiu Kepeng, Wang Zhi, Wang Huan. Calculation of equivalent elastic properities of chiral honeycombs [C]//The 7th Youth Science and Technology Forum of Chinese Aeronautical Society, 2016. (in Chinese)
[14]魏路路,余强,赵轩,等.内凹-反手性蜂窝结构的面内动态压溃性能研究[J].振动与冲击, 2021, 40(4): 261-269. Wei Lulu, Yu Qiang, Zhao Xuan, et al. In-plane dynamic crushing characteristics of re-entrant anti-trichiral honeycomb[J]. Journal of Vibration and Shock, 2021, 40(4): 261-269. (in Chinese)
[15]Wu W W,Hu W X,Qian G A,et al. Mechanical design and multifunctionalapplicationsofchiralmechanical metamaterials:A review[J]. Materials & Design,2019,180:107950.
[16]Xia R,Song X K,Sun L J,et al. Mechanical properties of 3D isotropic anti‐tetrachiral metastructure[J]. Physica Status Solidi(B),2018,255(4):1700343.
[17]Wu W W,Qi D X,Liao H T,et al. Deformation mechanism of innovative 3D chiral metamaterials[J]. Scientific Reports,2018,8(1):1-10.
[18]Duan S Y,Wen W W,Fang D N. A predictive micropolar continuum model for a novel three-dimensional chiral lattice with size effect and tension-twist coupling behavior[J]. Journal of the Mechanics and Physics of Solids,2018,121:23-46.
[19]Ha C S,Plesha M E,Lakes R S. Chiral three-dimensional lattices with tunable Poisson’s ratio[J]. Smart Materials and Structures,2016,25(5):054005.
[20]Ebrahimi H,Mousanezhad D,Nayeb-Hashemi H,et al. 3D cellular metamaterials with planar anti-chiral topology[J]. Materials & Design,2018,145:226-231.
[21]Fu M H,Liu F M,Hu L L. A novel category of 3D chiral material with negative Poisson’s ratio[J]. Composites Science and Technology,2018,160:111-118.
[22]Frenzel T,Hahn V,Ziemke P,et al. Large characteristic lengths in 3D chiral elastic metamaterials[J]. Communications Materials,2021,2(1):1-9.
[23]Farrugia P S,Gatt R,Grima J N.Anovel three‐dimensional anti‐tetrachiral honeycomb[J]. Physica Status Solidi(B),2019,256(1):1800473.
[24]Fu M H,Zheng B B,Li W H. A novel chiral three-dimensional material with negative Poisson’s ratio and the equivalent elastic parameters[J]. Composite Structures,2017,176:442-448.
[25]盧子兴,李康.手性和反手性蜂窝材料的面内冲击性能研究[J].振动与冲击, 2017, 36(21) : 16-22. Lu Zixing, Li Kang. In-plane dynamic crushing of chiral and anti-chiral honeycombs[J]. Journal of Vibration and Shock,2017, 36(21): 16-22. (in Chinese)
[26]Prall D,Lakes R S. Properties of a chiral honeycomb with a Poisson’s ratio of-1[J]. International Journal of Mechanical Sciences,1997,39(3):305-314.
[27]Alderson A,Alderson K L,Attard D,et al. Elastic constants of 3-,4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science & Technology,2010,70(7):1042-1048.
[28]Lorato A,Innocenti P,Scarpa F,et al. The transverse elastic properties of chiral honeycombs[J]. Composites Science and Technology,2010,70(7):1057-1063.
[29]Bacigalupo A,Gambarotta L. Homogenization of periodic hexa- and tetrachiral cellular solids[J]. Composite Structures,2014,116:461-476.
[30]Mousanezhad D,Haghpanah B,Ghosh R,et al. Elastic properties of chiral,anti-chiral,and hierarchical honeycombs:A simple energy-based approach[J]. Theoretical and Applied Mechanics Letters,2016,6(2):81-96.
[31]Liu X N,Huang G L,Hu G K. Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices[J]. Journal of the Mechanics and Physics of Solids,2012,60(11):1907-1921.
[32]Chen Y,Scarpa F,Liu Y,et al. Elasticity of anti-tetrachiral anisotropic lattices[J]. International Journal of Solids and Structures,2013,50(6):996-1004.
[33]Yuan Z H,Cui Z M,Ju J. Micropolar homogenization of wavy tetra-chiral and tetra-achiral lattices to identify axialshear coupling and directional negative Poisson’s ratio[J]. Materials & Design,2021,201:109483.
[34]Zhong R C,Fu M H,Yin Q Y,et al. Special characteristics of tetrachiral honeycombs under large deformation[J]. International Journal of Solids and Structures,2019,169:166-176.
[35]Hu L L,Ye W K,Wu Z J. Mechanical property of antitrichiral honeycombs under large deformation along the xdirection[J]. Thin-Walled Structures,2019,145:106415.
[36]Hu L L,Wu Z J,Fu M H. Mechanical behavior of antitrichiral honeycombs under lateral crushing[J]. International Journal of Mechanical Sciences,2018,140:537-546.
[37]Hu L L,Luo Z R,Yin Q Y. Negative Poisson’s ratio effect of re-entrant anti-trichiral honeycombs under large deformation[J]. Thin-Walled Structures,2019,141:283-292.
[38]Qi D X,Zhang P,Wu W W,et al. Innovative 3D chiral metamaterials under large deformation:Theoretical and experimental analysis[J]. International Journal of Solids and Structures,2020,202:787-797.
[39]Alderson A,Alderson K L,Chirima G,et al. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs[J]. Composites Science and Technology,2010,70(7):1034-1041.
[40]Lakes R. Cellular solid structures with unbounded thermal expansion[J].Journal of Materials Science Letters,1996,15(6):1-10.
[41]Ha C S,Plesha M E,Lakes R S. Chiral three‐dimensional isotropic lattices with negative Poisson’s ratio[J]. Physica Status Solidi(B),2016,253(7):1243-1251.
[42]Mizzi L,Attard D,Gatt R,et al. An analytical and finite element study on the mechanical properties of irregular hexachiral honeycombs[J]. Smart Materials and Structures,2018,27(10):105016.
[43]Mizzi L,Attard D,Gatt R,et al. Influence of translational disorderonthemechanicalpropertiesofhexachiral honeycomb systems[J]. Composites Part B:Engineering,2015,80:84-91.
[44]Pozniak A A,Wojciechowski K W. Poisson’s ratio of rectangular anti-chiral structures with size dispersion of circular nodes[J]. Physica Status Solidi(B),2014,251(2):367-374.
[45]Duan S Y,Xi L,Wen W W,et al. A novel design method for 3D positive and negative Poisson’s ratio material based on tension-twist coupling effects[J]. Composite Structures,2020,236:111899.
[46]Zhao W,Zhu J,Liu L W,et al. Analysis of small-scale topology and macroscale mechanical properties of shape memory chiral-lattice metamaterials[J]. Composite Structures,2021,8:113569.
[47]張会凯.拓扑优化方法的力学超材料设计[D].大连:大连理工大学, 2019. Zhang Huikai. Mechanical metamaterial design using topology optimizationmethod[D].Dalian:DalianUniversityof Technology, 2019. (in Chinese)
[48]Qiu K P,Wang R Y,Zhu J H,et al. Optimization design of chiral hexagonal honeycombs with prescribed elastic properties under large deformation[J]. Chinese Journal of Aeronautics,2020,33(3):902-909.
[49]Qi D X,Lu Q Y,He C W,et al. Impact energy absorption of functionally graded chiral honeycomb structures[J]. Extreme Mechanics Letters,2019,32:100568.
[50]Wu W W,Tao Y,Xia Y,et al. Mechanical properties of hierarchical anti-tetrachiral metastructures[J].Extreme Mechanics Letters,2017,16:18-32.
[51]Geng L C,Ruan X L,Wu W W,et al. Mechanical properties of selective laser sintering(SLS)additive manufactured chiral auxetic cylindrical stent[J]. Experimental Mechanics,2019,59(6):913-925.
[52]Ma C,Lei H H,Liang J,et al. Macroscopic mechanical response of chiral-type cylindrical metastructures under axial compression loading[J]. Materials & Design,2018,158:198-212.
[53]Wu W W,Geng L C,Niu Y H,et al. Compression twist deformation of novel tetrachiral architected cylindrical tube inspired by towel gourd tendril[J]. Extreme Mechanics Letters,2018,20:104-111.
[54]段富海,初雨田,关文卿,等.变形机翼的发展现状综述[J].机电工程技术, 2021, 50(1): 12-18. Duan Fuhai, Chu Yutian, Guan Wenqing. et al. A review of development status of morphing wing [J]. Mechanical & Electrical Engineering Technology, 2021, 50(1): 12-18. (in Chinese)
[55]张尧,张婉,别大卫,等.智能变体飞行器研究综述与发展趋势分析[J].飞航导弹, 2021 (6) : 14-23. Zhang Yao, Zhang Wan, Bie Dawei, et al. Review and development trend analysis of intelligent morphing aircraft [J]. Aerodynamic Missile Journal, 2021 (6) : 14-23. (in Chinese)
[56]王晓明.压电驱动柔性翼面的优化设计与变形控制方法[D].大连:大连理工大学, 2018. Wang Xiaoming. Optimal design and shape control method for piezo-actuatedflexiblewingsurface[D].Dalian:Dalian University of Technology, 2018. (in Chinese)
[57]Bettini P,Airoldi A,Sala G,et al. Composite chiral structures for morphing airfoils:Numerical analyses and development of a manufacturing process[J]. Composites Part B:Engineering,2010,41(2):133-147.
[58]Vo?R,Strohmeyer D,Sachau D,et al. The Adaptive wing projekt(DLR):Survey on targets and recent results from active/adaptive structures viewpoint[C]//Proceedings of the 10th International Conference on Adaptive Structures and Technologies(ICAST′99),1999.
[59]Campanile L F,Sachau D. The Belt-Rib concept:A structronic approach to variable camber[J]. Journal of Intelligent Material Systems & Structures,2000,11(3):215-224.
[60]Bornengo D,Scarpa F,Remillat C. Evaluation of hexagonal chiral structure for morphing airfoil concept[J]. Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2005,219(3):185-192.
[61]Spadoni A,Ruzzene M. Numerical and experimental analysis of the static compliance of chiral truss-core airfoils[J]. Journal of Mechanics of Materials and Structures,2007,2(5):965-981.
[62]Spadoni A,Ruzzene M. Static aeroelastic behavior of chiralcore airfoils[C]//Proceedings of ICAST-Sixteenth International Conference onAdaptive Structures and Technologies,2005.
[63]Spadoni A,Ruzzene M. Static aeroelastic response of chiralcore airfoils[J]. Journal of Intelligent Material Systems and Structures,2007,18(10):1067-1075.
[64]Martin J,Heyder‐Bruckner J J,Remillat C,et al. The hexachiral prismatic wingbox concept[J]. Physica Status Solidi(B),2008,245(3):570-577.
[65]Heo H, Ju J, Kim D M, et al. Passive morphing airfoil with honeycombs[C]//ProceedingsoftheASMEInternational Mechanical Engineering Congress and Exposition, 2011.
[66]Vos R,Barrett R. Mechanics of pressure-adaptive honeycomb and its application to wing morphing[J]. Smart Materials and Structures,2011,20(9):094010.
[67]趙显伟.可变形蜂窝结构的力学性能分析[D].哈尔滨:哈尔滨工业大学, 2013. Zhao Xianwei. The analysis of mechanical properties of morphing honeycomb structures[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese)
[68]白子龙.智能材料研究进展及应用综述[J].军民两用技术与产品, 2020 (3) : 15-20. Bai Zilong. Review on research progress and application of intelligent materials[J]. Dual Use Technologies & Products, 2020 (3) : 15-20. (in Chinese)
[69]冷劲松,孙健,刘彦菊.智能材料和结构在变体飞行器上的应用现状与前景展望[J].航空学报, 2014, 35(1) : 29-45. Leng Jinsong, Sun Jian, Liu Yanju. Application status and future prospect of smart materials and structures in morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 29-45. (in Chinese)
[70]王曦,付晨.复合材料转向架构架及其疲劳损伤分析方法研究综述[J].北京交通大学学报, 2019, 43(1): 42-53. Wang Xi, Fu Chen. Review of composite bogie frame and its fatigue damage analysis methods[J]. Journal of Beijing Jiaotong University, 2019, 43(1) : 42-53. (in Chinese)
[71]张恩奋.无人机结构用复合材料及其制造技术综述[J].科技风, 2018 (11) : 1. ZhangEnfen.Reviewofcompositematerialsand manufacturing technology for UAV[J]. Technology Wind, 2018(11) : 1. (in Chinese)
[72]程健男,徐福泉,张体磊.树脂基复合材料在直升机的应用及其制造技术[J].航空科学技术, 2021, 32(1) : 109-114. Cheng Jiannan, Xu Fuquan, Zhang Tilei. Application and manufacturing technology of composites in helicopter[J]. Aeronautical Science & Technology, 2021, 32(1): 109-114. (in Chinese)
[73]孙侠生,肖迎春,白生宝,等.民用飞机复合材料结构健康监测技术研究[J].航空科学技术, 2020, 31(7) : 53-63. Sun Xiasheng, Xiao Yingchun, Bai Shengbao, et al. Research on structural health monitoring technology of civil aircraft composites[J]. Aeronautical Science & Technology, 2020, 31(7) : 53-63. (in Chinese)
[74]Airoldi A,Bettini P,Boiocchi M,et al. Composite elements for biomimetic aerospace structures with progressive shape variation capabilities[J]. Advances in Technology Innovation,2016,1(1):13.
[75]Airoldi A,Crespi M,Quaranti G,et al. Design of a morphing airfoil with composite chiral structure[J]. Journal of Aircraft,2012,49(4):1008-1019.
[76]杨建楠,黄彬,谷小军,等.形状记忆合金力学行为与应用综述[J].固体力学学报, 2021, 42(4): 345-375. Yang Jiannan, Huang Bin, Gu Xiaojun, et al. A review of shape memory alloys: mechanical behavior and application[J]. Chinese Journal of Solid Mechanics, 2021, 42(4): 345-375. (in Chinese)
[77]李继威,张勇,陈继春.压电材料在飞行翼形控制方面的一些应用[J].电子元件与材料, 2009, 28(6): 74-78. Li Jiwei, Zhang Yong, Chen Jichun. Application to control airfoil of aerocraft using piezoelectric materials[J]. Electronic Components & Materials, 2009, 28(6) : 74-78. (in Chinese)
[78]Hassan M R,Scarpa F,Ruzzene M,et al. Smart shape memory alloy chiral honeycomb[J]. Materials Science and EngineeringA,2008,481(1):654-657.
[79]顏硕.基于NiTi形状记忆合金的柔性可变翼面设计[D].成都:电子科技大学, 2020. Yan Shuo. Research on morphing wing based on NiTi shape memory alloy[D]. Chengdu: University of Electronic Science and Technology of China, 2020. (in Chinese)
[80]Kamlet M,Gibbs Y. NASA tests new alloy to fold wings in flight[R]. NASA:Edwards,CA,USA,2018.
[81]Prajapati M,Mahapatra D R. Shape memory alloy-based active chiral composite cells[C]//Proceedings of the Active and Passive Smart Structures and Integrated Systems 2014,2014.
[82]Prajapati M,Mahapatra D R. Shape memory alloy-based active chiral composite cells[C]//Active and Passive Smart Structures and Integrated. International Society for Optics and Photonics,2014.
[83]刘京彪.形状记忆聚合物及其复合材料性能与热力学行为研究[D].哈尔滨:哈尔滨工程大学, 2020. Liu Jingbiao. Study on the performances and thermodynamic behavior of shape memory polymers and their composites[D]. Harbin: Harbin Engineering University, 2020. (in Chinese)
[84]杜海洋.形状记忆聚合物的力学性能分析及其智能模具制备[D].哈尔滨:哈尔滨工业大学, 2018. Du Haiyang. Mechanical behavior analysis and smart mandrels fabrication based on shape memory polymers[D]. Harbin: Harbin Institute of Technology, 2018. (in Chinese)
[85]Rossiter J,Takashima K,Scarpa F,et al. Shape memory polymer hexachiral auxetic structures with tunable stiffness[J]. Smart Materials and Structures,2014,23(4):045007.
[86]Neville R M,Chen J,Guo X,et al. A Kirigami shape memory polymer honeycomb concept for deployment[J]. Smart Materials and Structures,2017,26(5):05LT03.
[87]Huang J,Zhang Q H,Scarpa F,et al. Shape memory polymer-basedhybridhoneycombstructureswithzero Poisson’s ratio and variable stiffness[J]. Composite Structures,2017,179:437-443.
[88]Tao K,Chen Z S,Yi H P,et al. Hierarchical honeycombstructured electret/triboelectric nanogenerator for biomechanical and morphing wing energy harvesting[J]. Nano-micro Letters,2021,13(1):1-16.
[89]Wickramasinghe V,Chen Y,Martinez M,et al. Design and verification of a smart wing for an extreme-agility micro-airvehicle[J]. Smart Materials and Structures,2011,20(12): 125007.
[90]Henry A C,Molinari G,Rivas-Padilla J R,et al. Smart morphing wing:optimization of distributed piezoelectric actuation[J].AIAAJournal,2019,57(6):2384-2393.
[91]ChillaraV,RamanathanA,DapinoM.Self-sensing piezoelectric bistable laminates for morphing structures[J]. Smart Materials and Structures,2020,29(8):085008.
[92]段富海,初雨田,關文卿,等.变形机翼的关键技术研究现状及其展望[J].空军预警学院学报, 2020, 34(3): 203-209. Duan Fuhai, Chu Yutian, Guan Wenqing, et al. Research status and prospect of key technology of morphing wing[J]. Journal of Air Force Early Warning Academy, 2020, 34(3): 203-209.(in Chinese)
Research Progress of Deformable Aircraft Wing Based on Chiral Superstructures Design
Liu Kai1,2,Cao Xiaofei1,2,Li Ying1,2,Fang Daining1,2
State Key Laboratory of Explosive Science and Technology,Beijing Institute of Technology,Beijing 100081,China
Abstract: Safety, stability and efficiency are the key issues in the field of aircraft wing structure design. Wing is one of the main components to provide lift, and deformable wing has great potential in improving the overall performance of aircraft. The development of new materials represented by smart materials has revolutionized the wing flexible skin, driving device, control technology and lightweight structure, and expanded the application range of chiral superstructures. The deformable wing designed based on chiral structure, aerodynamic performance analysis of aircraft wing and advanced preparation technology can change its wing shape at different flight speeds, flight slopes and surrounding flow fields, so as to improve flight efficiency, which is not only the frontier field of aircraft wing structure design, but also an important development direction in the future. This paper introduces the design method and theoretical method of chiral superstructures, and summarizes the research progress of deformable aircraft wing at home and abroad so as to provide
3336500338247
