基于原位共角椭偏与反射谱的TiO2薄膜光学常数分析
2022-03-10孙晓娟韩培高隽方蓥郝殿中
孙晓娟,韩培高,隽方蓥,郝殿中
(曲阜师范大学 物理工程学院 物理系,曲阜 273165)
引 言
近年来,TiO2以其高催化性、高稳定性、强氧化性以及强紫外线吸收能力,且无毒无害、无刺激性、低成本和不会造成二次污染等优点,被广泛应用于废水处理、自清洁、空气净化、太阳能、光电转化、光催化、防晒护肤等众多领域[1]。同时,因TiO2较大的带隙、较高的折射率,又是常用的可见和红外介质膜镀膜材料[2-5]。TiO2薄膜的制备方法包含电子束蒸发法、溶胶-凝胶法、浸渍提拉法、气相合成法、平面磁控溅射法、分散法等[4-10]。其中溶胶-凝胶法具有操作简单、成本低、制作周期短、适合大面积镀膜等优点[4,6-7],但相较于原子层沉积、电子束蒸发、磁控溅射等方法制备的较致密TiO2薄膜,溶胶-凝胶法制备的TiO2薄膜通常存在一定的孔隙率,且孔隙率、折射率等受溶胶-凝胶制备方法中前驱体选择、温度、旋涂速率等多种因素的影响,因而不同的制备条件得到的TiO2薄膜通常具有不同的孔隙率、折射率色散等光学特性[7,9],影响薄膜的反射、透射等性能。因此,对溶胶-凝胶法制备的TiO2薄膜光学常数的检测分析具有重要意义。
目前,测量薄膜光学常数的方法有椭偏测量法、干涉法、光度法和棱镜耦合法等[7]。其中,椭偏法测量具有对样品无破坏性、灵敏度高、精度高、对环境的非苛刻性等优点,逐渐成为薄膜光学常数测量的一种重要手段,为薄膜和光电器件结构设计与性能调控提供了有力的基础光学数据和理论指导[11-16]。在椭偏光谱分析中,薄膜的色散模型选择非常重要,对TiO2薄膜的椭偏分析通常采用Cauchy色散模型[1],关于New Amorphous色散模型应用于溶胶-凝胶法制备的TiO2薄膜椭偏光谱分析的研究较少,本文中介绍利用New Amorphous模型在1.55eV~4.00eV波段对溶胶-凝胶法制备的不同厚度TiO2薄膜椭偏光谱的拟合分析,研究了薄膜折射率色散、孔隙率及厚度随旋涂层数的变化关系。薄膜光学常数的椭偏光谱拟合测量方法是一种间接测量方法,除薄膜色散模型的选择之外,对拟合结果的验证也是椭偏法的重要内容。作者提出了原位共角椭偏与反射谱的测量方法,通过原位测量反射谱与椭偏拟合结果反演理论反射谱的对比,对椭偏拟合结果进行验证,为微区、非均匀薄膜情况下光学常数的椭偏测量与验证提供了参考。
1 实 验
1.1 样品制备
以正丁醇和二异丙基钛酸酯配置溶胶。将10mL正丁醇(质量分数为0.998)和0.75mL的二异丙基钛酸酯(质量分数为0.75)混合,搅拌均匀后得到TiO2溶胶,将制备好的溶胶在室温下老化24h以备用。在清洁的环境下,用匀胶机在清洁的单晶硅基片上镀膜,采用多步旋涂法制备TiO2薄膜,分步旋涂转速分别为700r/min和4000r/min,旋涂时间分别为5s和25s,每次旋涂结束后立即将样品放在120℃的加热板上加热10min,待样品冷却至室温后重复上述操作,制备不同旋涂层数的薄膜,涂完最后一层膜以后,将样品放入200℃的烘干箱中干燥30min,然后放入500℃的马弗炉里加热30min,得到最终样品。本实验中针对旋涂层数为1层~6层的样品进行研究,对应样品分别用d1~d6表示。
1.2 样品测试
采用热场发射扫描电镜(scanning electron micro-scopy,SEM)(Sigma 500,ZEISS)对TiO2薄膜表面形貌进行观察。使用椭圆偏振光谱仪(UVISEL型)测量薄膜的椭偏光谱,光源为150W氙灯,实验中选取测量的波段为1.55eV~4.00eV,入射角为70°,起偏棱镜方位为45°,光弹调制器光轴方位为0°,调制频率为50kHz,检偏器方位为45°。利用椭偏光谱仪,在相同的70°入射角度下,原位测量样品的反射光谱,参考片为单晶硅片。
2 结果与讨论
2.1 SEM分析
通过对样品薄膜表面的SEM测量,发现d1~d6样品的TiO2薄膜表面形貌基本相同,即旋涂薄膜表面形貌基本不受旋涂层数影响。图1是d3样品的SEM表面形貌图。从图1中可以看出,薄膜表面较均匀的分布着溶胶-凝胶方法制备的薄膜中常见的孔隙,薄膜表面整体比较平整,在薄膜表面观察不到明显的裂纹存在。

Fig.1 SEM image of TiO2 thin films surface
2.2 TiO2薄膜的椭偏光谱分析
椭偏光谱测量技术作为一种灵敏的、非接触、无损测量技术,通过测量偏振光经过样品反射或透射后偏振态的改变得到椭偏光谱,然后根据样品结构建立结构模型,对结构模型中的材料选择合适的色散模型,对椭偏光谱进行拟合分析,来获取样品的光学参量,是一种间接测量技术。在通常的反射测量情况下,椭偏参量ρ定义如下[17-18]:
式中,rp和rs分别代表p光和s光的振幅反射系数;tanΨ是振幅反射系数比的模,Ψ∈[0°,90°];Δ是振幅反射系数比的幅角,Δ∈[0°,360°]。UVISEL型椭偏光谱仪光路元件的设置顺序为氙灯光源、起偏器、样品、光弹调制器、检偏器、单色仪,在起偏器、光弹调制器、检偏器相对入射平面的方位分别为45°,0°,45°的设置情况下,椭偏光谱中间参量Is,Ic分别为:
Is=sin(2Ψ)sinΔ
(2)
Ic=sin(2Ψ)cosΔ
(3)
椭偏参量Ψ和Δ由Is和Ic算得出,因此Ψ,Δ为间接参量,非直接测量参量,同时受限于sin(2Ψ)在Ψ接近45°时随Ψ变化不明显,计算误差较大,以及数值上关于45°的镜像效应,在椭偏光谱拟合分析中通常采用对Is,Ic色散曲线进行拟合的方法,而不是对Ψ,Δ色散曲线进行直接拟合计算。
采用起偏器、光弹调制器、检偏器相对入射平面的方位分别为45°,0°,45°的设置,在70°入射角下,分别测量了d1~d6样品在1.55eV~4.00eV区间的椭偏反射光谱。
考虑到TiO2薄膜含有一定的孔隙率,且SEM观察到的薄膜表面形貌基本不受旋涂层数影响,建立了如图2所示的样品结构模型,用来对样品的椭偏光谱进行拟合分析。在材料色散模型选择中,单晶硅、SiO2天然氧化层均为常规标准材料,采用标准参考文件,环境空气取折射率n=1,空气消光系数k=0。TiO2层的色散模型采用New Amorphous色散模型,该色散模型是由Fourouchi & Bloomer的Amorphous模型发展来的[18],该色散模型可以看作是能带带隙之上的单振子模型,带隙之下消光系数k=0,视为无吸收,折射率n和消光系数k可以分别表示为:
C=2fjΓj(ωj-ωg)
(7)
式中,n∞为长波折射率,ωg为带隙能量,ωj为最大吸收能量,fj为振子强度,Γj为展宽因子。

Fig.2 Model of film structure with voids for ellipsometry fitting
图3a、图3b分别是对d1~d6样品椭偏光谱Is,Ic色散曲线的测量和拟合结果。可以看出,在1.55eV~4.00eV波段内,拟合得到的Is与Ic色散曲线与实测曲线均吻合较好。
表1为拟合得到的不同旋涂层数的TiO2薄膜的厚度和孔隙率结果。可以看出,在实验采用的旋涂参量下,TiO2薄膜每层旋涂的厚度约为8.9nm,旋涂层数的增加与薄膜厚度的增加成较好的线性关系,因此可以在一定程度上通过控制旋涂层数实现对薄膜厚度的控制。同时可以看到,薄膜的孔隙率均为15%~16%,即薄膜孔隙率基本不随旋涂层数变化,这与SEM观察到的不同旋涂层数样品表面形貌基本相同是一致的。

Fig.3 Results of elliptic polarization measurement and fitting of TiO2 thin films with different spin coating layers
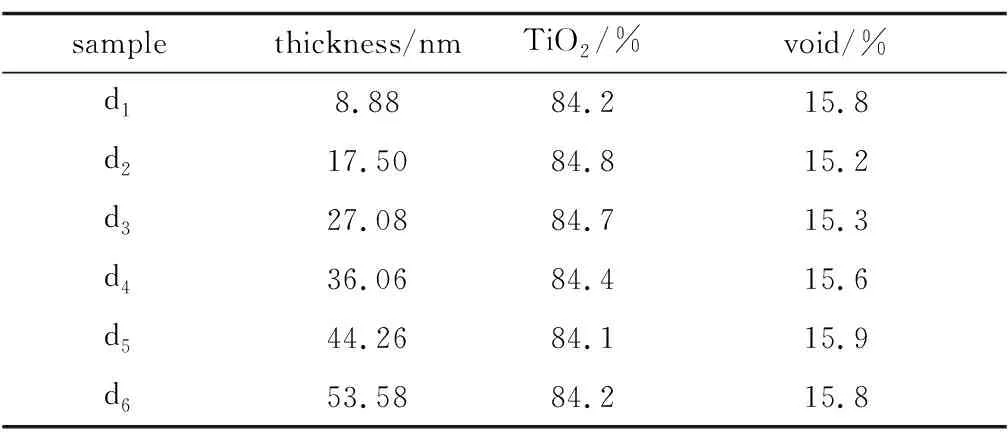
Table 1 Thickness and porosity of TiO2 thin films with different spin coating layers
椭偏光谱拟合得到的TiO2薄膜New Amorphous色散模型中参数值如表2所示。

Table 2 Fitted parameter values of new amorphous dispersion model
拟合得到的TiO2薄膜的带隙ωg≈3.1eV,这一参量跟参考文献[19]和参考文献[20]中TiO2薄膜的带隙ωg≈2.9eV~3.2eV相吻合。
将表2中所得的参量代入New Amorphous色散模型中,得到TiO2薄膜的折射率n和消光系数k色散曲线,如图4所示。
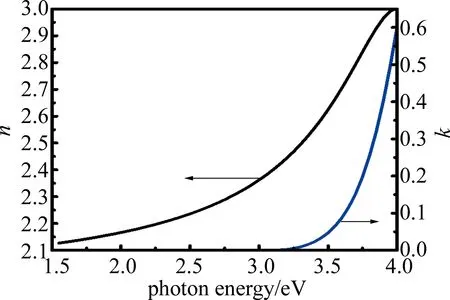
Fig.4 Refractive index n and extinction coefficient k dispersion curves of TiO2 thin films
由图4可见,在1.55eV~4.00eV波段内,TiO2薄膜的折射率处于2.1~3.0之间,薄膜对于3.1eV以下波段消光系数k=0,是无吸收的。
2.3 光学常数的反演
椭偏光谱作为一种薄膜光学常数的间接测量方法,对拟合结果可靠性有必要进行验证。由椭偏光谱拟合得到的折射率色散及薄膜厚度等光学常数结果,通过计算可以反演得到样品的理论反射光谱,将理论反射光谱与实测反射光谱进行比较,两者的符合程度是检验椭偏光谱拟合结果可靠性的便捷方法之一。
在椭偏光谱测试中,起偏器方位45°、光弹调制器方位0°、检偏器方位45°,由琼斯矩阵分析可知,探测器得到的直流信号与入射光强、样品反射率成正比。实验中以单晶硅片为参考基片,与椭偏光谱测量共角度70°下,原位测量了样品相对单晶硅的反射光谱Rr,得到了样品实际反射率色散曲线Rf,换算过程中单晶硅片理论反射率RSi的计算采用了单晶硅理论复折射率色散值并考虑了单晶硅表面天然氧化层的影响。
图5为根据椭偏光谱拟合所得光学常数通过薄膜干涉理论计算反演得到反射谱与原位共角实测反射谱的对比。从图中可以看到,不同厚度样品的理论反射率曲线与实测反射率曲线在峰位、形状上总体吻合均较好,表明对椭偏光谱拟合的结果是可靠的。同时注意到,反演得到的反射率曲线与实测反射率曲线在强度值上最大有3%左右的偏差,可以认为这是由薄膜表面及内部孔隙界面散射所致,同时表面微尘散射和氙灯光源强度的稳定性也会影响反射率测量值的大小。
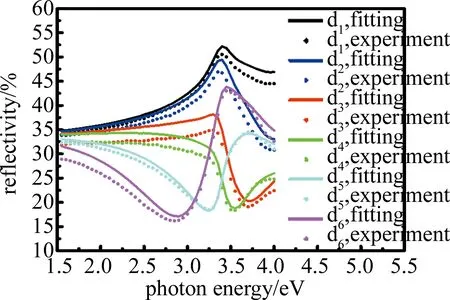
Fig.5 Comparison of reflectivity fitting value and measurement value of TiO2 thin film with different thickness
3 结 论
利用New Amorphous色散模型对溶胶-凝胶TiO2薄膜1.55eV~4.00eV波段的椭偏光谱进行了拟合,得到了TiO2薄膜的带隙、复折射率和色散,TiO2薄膜厚度与旋涂层数成正比,每层的旋涂厚度约为8.9nm,可以通过旋涂层数控制薄膜厚度,薄膜孔隙率约为15%~16%,且随旋涂层数变化不明显。利用原位共角反射光谱对椭偏光谱拟合结果进行了验证。
