饱和承压水砂层排水诱导驱替注浆技术研究

邓洪亮，王守凡，李小鹏

(1.北京工业大学城市建设学部，北京 100124；2.北京市政路桥股份有限公司，北京 100045)

0 引言

目前，隧道及地下工程领域发展迅速，对注浆技术不断提出新的要求。北京地铁17号线工程西坝河站—太阳宫站区间联络线段及渡线段开挖断面地层为饱和承压水砂层，砂层位于黏土层之间，含承压水且砂层已达到饱和状态，承压水水头位于黏土层上方。开挖断面砂层自身稳定性差，且存在承压水，为隧道开挖带来极大难题。此外，由于承压水的影响，浆液在砂层中难以扩散，饱和承压水砂层注浆面临新的难题。

砂土孔隙相比其他土体大，注浆时一般以渗透注浆为主，已有学者对渗透注浆理论和技术开展了大量研究。基于达西定律建立的球形扩散理论与柱形扩散理论成为诸多学者研究渗透注浆理论的基础。Bouchelaghem等[1]得到了基于Bear的空间体积平均统计模型的混相浆液在饱和变形多孔介质中的传播规律。Saada等[2]、周军霞等[3]和李术才等[4]分别考虑了渗滤效应和浆液黏度时变性对砂土渗透注浆的影响。叶飞等[5-6]、张连震等[7]分别考虑了驱替效应以及动水条件对渗透注浆的影响，并对动水条件下的渗透注浆设计及工艺提出了改进方法。此外，一些学者根据工程经验对富水区地层注浆施工提出改进方案[8-9]。即使如此，目前注浆理论与技术的发展仍然满足不了工程的需要，对注浆技术的研究仍显得十分重要。

诱导注浆技术是一种新兴的注浆方法，其目的是通过物理以及化学作用，人为诱导浆液定向扩散，达到预期的加固效果。黄明利等[10]通过在土体中布设诱导孔改变土体在注浆过程中的应力状态，从而控制劈裂缝扩展方向，达到诱导劈裂注浆的目的。冯冰[11]提出了布设卸压孔诱导注浆的方法，并采用理论计算与数值模拟的方法分析了最佳的布孔方式，研究了卸压诱导注浆扩散机制。此2种诱导注浆方法适用于具有一定强度的硬质土层，对于饱和承压水砂层，劈裂注浆难以达到需求的加固强度。Whiffin[12]首次将微生物诱导碳酸钙沉淀(microbial induced calcite precipitation，MICP)方法应用于土体加固中，发现该方法可以显著提高砂土的剪切强度。彭劼等[13]通过试验验证了MICP注浆方法的可行性及加固效果。MICP方法适用的加固土层范围较广，但大量培养微生物需要高额花费，不适用于隧道工程大规模注浆。

目前，适用于饱和承压水砂层的诱导注浆方法及理论较少。针对饱和承压水砂层这一特殊地质条件，本文提出排水诱导驱替注浆技术，在饱和承压水砂层中施加注浆压力与排水压力，通过排水产生的抽吸压力诱导浆液在饱和承压水砂层中定向渗透扩散，对饱和承压水砂层预定区域进行加固。同以往注浆方法相比，排水诱导驱替注浆技术可解决饱和承压水砂层中承压水导致的压浆困难的问题，且可同时达到定向诱导注浆的效果。本文基于达西定律和质量守恒定律，推导注浆压力与排水压力作用下排水诱导驱替注浆渗流压力梯度空间分布方程，并结合饱和砂土定向诱导注浆试验对注浆压力与排水压力作用下排水诱导驱替注浆的渗流压力梯度空间分布进行研究。

1 排水诱导驱替注浆可行性分析

1.1 饱和砂土可注性分析

浆液性质及砂层自身性质决定了砂层的渗透注浆可注性，水泥类颗粒型浆液的流动性、稳定性和颗粒粒径等因素决定了这类浆液的可注性及适用范围，只有在浆液颗粒粒径小于岩土体孔隙的有效尺寸时，颗粒类浆液才具有可注性。

可注性判别由被注介质孔隙直径和注浆材料直径之间的关系比来确定。当浆液颗粒尺寸比被注介质孔隙尺寸小时浆液可充分注入，反之则不能注入。Burwell[14]、Mitchell[15]提出了可注性的判别参数和相应的判定标准。假定D15、D10分别为砂层颗粒级配曲线中颗粒质量分数小于15%和10%所对应的特征粒径，d85、d95分别为浆液颗粒级配曲线中颗粒质量分数小于85%和95%所对应的特征粒径，N=D15/d85，M=D10/d95。当N﹥24时，可注；当M﹥11时，可注；当N﹤11时，不能充分注入；当M﹤5时，不可注。但砂层复杂的孔隙结构很难通过简单的参数确定，所以不同可注入标准之间存在一定的差异。

1.2 排水诱导驱替注浆原理

砂层为多孔介质，一般而言，当土体的渗透系数大于10-5cm/s时，浆液扩散方式主要以渗透为主。当砂层为饱和承压水砂层时，承压水作为填充砂层孔隙的流体介质，具有传递压力的作用。在饱和承压水砂层中设置排水管，通过排水管在饱和承压水砂层中施加抽吸力，在排水管附近形成负压区域，诱导砂层中的承压水向排水管流动形成渗流通道，从而达到对浆液定向诱导的作用，其浆液锋面扩散示意如图1所示。

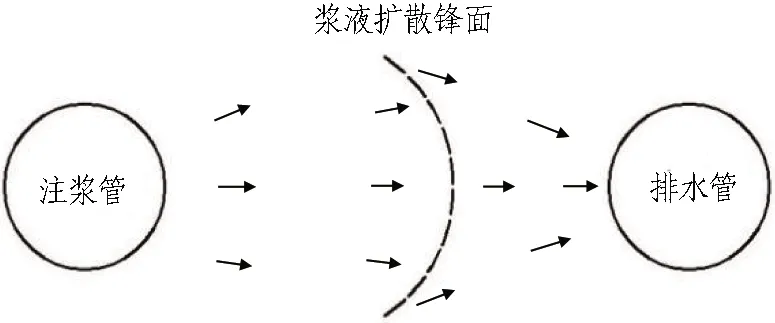
图1 排水诱导驱替注浆下浆液锋面扩散示意图

在饱和承压水砂层进行排水诱导驱替注浆时，如果在饱和承压水砂层内部一定区域内布置注浆管与排水管，注浆过程中持续施加注浆压力与排水压力，饱和承压水砂层中将形成高低压力场，浆液作为另一种流体将会向低压区渗流，排水产生的抽吸压力驱使浆液定向渗流，实现定向诱导注浆。

2 排水诱导驱替注浆理论

2.1 基本假定

1)假定饱和承压水砂层内部为封闭空间，与外界无法进行气体交换；

2)假定地下水初始压力和承压水水位在注浆过程中保持不变，且注浆过程中不考虑排水注浆对承压水初始压力状态的影响；

3)假定饱和承压水砂层内部各向均匀分布；

4)假定初始状态下砂层中承压水为地下静水，单一注浆或单一排水状态下，管壁周围流体渗流区域呈柱形分布，且管壁周围任意方向上流体的流速相等；

5)假定注浆过程中浆液不发生化学反应。

2.2 注浆压力与排水压力空间分布方程

砂层在天然状态下为多孔介质，浆液在砂层中的扩散方式以渗透为主。根据基本假定，与注浆管垂直的任意平面上，浆液以圆形向周围扩散。根据达西定律，浆液的渗流运动方程为

(1)

式中：vg为浆液渗流速度，cm/s；kg为浆液在土体中的渗透系数，cm/s；ρg为浆液密度，g/cm3；g为重力加速度，m/s2；pg为注浆压力，kPa；rg为浆液渗流半径，cm。

根据质量守恒定律，在相同时间内，扩散面A与扩散面B处浆液的流量相等，如图2所示。设Rg为注浆孔钻孔半径，vg0为注浆管管壁周围的浆液初始渗流速度，其计算可参考文献[16]。根据质量守恒定律可得

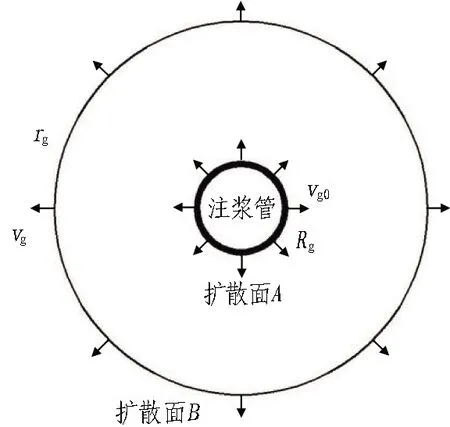
图2 浆液渗流扩散平面图

2πRgvg0=2πrgvg。

(2)

根据式(2)，浆液扩散区域任一点的流速用浆液初始渗流速度表示为

(3)

由式(1)和式(3)可得注浆压力梯度空间分布方程为

(4)

将式(4)移项积分可得注浆压力空间分布方程为

(5)

设初始注浆压力为pg0。当rg=Rg时，pg=pg0，将边界条件代入式(5)，可得

(6)

将式(6)代入式(5)中，可得注浆压力空间分布方程为

(7)

根据文献[17]，浆液在砂层中的渗透系数计算公式为

(8)

式中：kw为水在砂层中的渗透系数，cm/s；μw为水的动力黏度，mPa·s；μg为浆液动力黏度，mPa·s。

将式(8)代入式(7)，可得注浆压力空间分布方程为

(9)

对于饱和承压水砂层排水时，水在砂层中的渗流运动符合达西定律，排水压力梯度方向与注浆时方向相反，故排水压力梯度空间分布方程为

(10)

式中：pw为排水压力，kPa；rw为排水渗流半径，cm；vw0为排水管管壁周围水的初始渗流速度，cm/s；ρw为水密度，g/cm3；Rw为排水孔钻孔半径，cm。

排水过程中排水压力空间分布方程为

(11)

式中pw0为初始排水压力，kPa。

2.3 排水诱导驱替注浆渗流压力场空间分布方程

在自然状态下，注浆管周围的土体各个方向上的孔隙水压力相等。在注浆管周围的压力区内部布置排水管并施加排水压力，饱和承压水砂层内部排水管周围产生负压区域，负压通过承压水向注浆管附近传递，此时，在注浆管和排水管之间出现低压区。注浆管与排水管之间的渗流压力由注浆压力和排水压力组成，渗流压力场分布如图3所示。

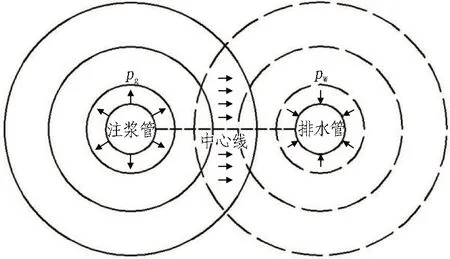
图3 排水诱导驱替注浆下的渗流压力场分布

设注浆管与排水管之间的距离为L，注浆管半径与排水管半径均为R，注浆管与排水管中心连线为渗流场压力中心线，土体中浆液扩散半径为r，则rw=L-r。渗透注浆过程中，渗流压力场中注浆压力与排水压力相互影响。假设注浆压力与排水压力同时作用下渗流压力为ph，根据式(4)、式(8)和式(10)可得渗流压力场中心线上渗流压力梯度空间分布方程为

(12)

对式(12)求导，可得渗流压力梯度空间分布方程的导数为

(13)

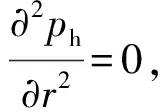
(14)

将一元二次方程移项变换，式(14)可变换为

(15)

(16)

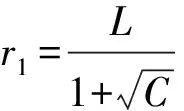
对于渗透注浆而言，通常以压力梯度作为渗透注浆发生的判别依据，当土体内部渗流压力梯度大于启动梯度时，饱和承压水砂层内部即可实现渗透注浆。流体在多孔介质中流动时，多孔介质中的孔隙可以等效为半径r0的毛细管，依据杨志全等[18]的研究，等效毛细管的半径可表示为

(17)

式中φ0为砂层孔隙率。

假设λ0为浆液启动梯度，依据杨秀竹等[19]的研究，流体在多孔介质中的启动梯度

(18)

式中τ0为流体的屈服应力，可参考文献[20]取值。

将式(17)代入式(18)，则饱和承压水砂层注浆启动梯度计算公式为

(19)

根据公式推导结果可知，当渗流场压力梯度λ大于启动梯度λ0时，浆液可贯通渗流场。

2.4 理论适用条件

假设渗流场同时施加注浆压力与排水压力下浆液渗流扩散速度为vh，将式(12)代入式(1)并简化可得

(20)

根据文献[21]，流体雷诺数计算公式为

(21)

式中d为土体颗粒的有效直径，一般用d10表示，mm。

本文推导的理论公式基于达西定律，根据文献[22]可知，达西定律适用于雷诺数小于5的渗流运动。对于本文推导理论，式(21)计算雷诺数小于5，即可满足本文理论公式的使用条件。

3 数值分析

北京地铁17号线工程西坝河站—太阳宫站区间渡线段与联络线段开挖饱和承压水砂层为中粗砂层，渡线段渗透系数kw=0.02 cm/s，浆液黏度为10.24 mPa·s，计算得到浆液在饱和承压水砂层中的渗透系数kg=0.002 cm/s。令初始注浆压力pg0等于初始排水压力pw0，其取值与初始渗流速度取值见表1。管间距L分别取70 cm、80 cm和90 cm。

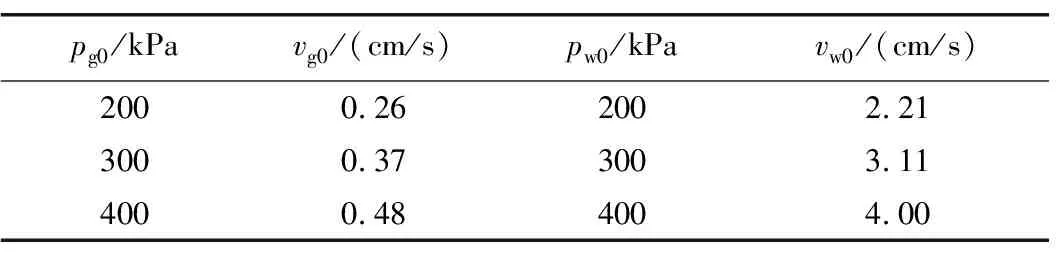
表1 初始压力与初始渗流速度取值

根据本文推导的渗流压力梯度空间分布方程，不同初始注浆压力与排水压力条件下的渗流压力梯度空间分布如图4所示。

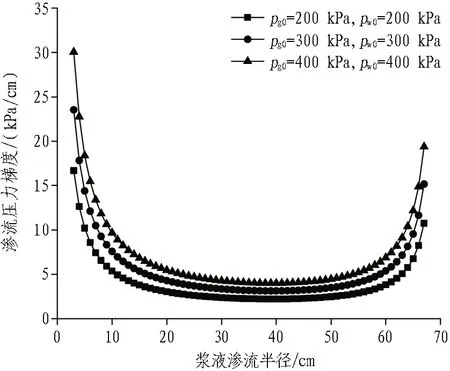
(a)L=70 cm

由于浆液的启动梯度很小，可认为以上计算渗流压力梯度满足贯通要求。根据图4中不同初始注浆压力与排水压力条件下渗流压力梯度空间分布曲线可知：

1)注浆管与排水管周围渗流压力梯度较大，渗流压力梯度曲线在注浆管与排水管周围变化较为显著，在渗流场中央变化较为平缓。

2)不同初始注浆压力和排水压力条件对渗流压力梯度有显著影响；渗流场可叠加的前提下，由于注浆压力与排水压力同时作用于渗流场，不同初始注浆压力与排水压力条件下，渗流压力梯度空间分布曲线均呈现先递减后递增的规律。渗流压力梯度空间分布曲线最低点大于启动梯度时，可实现定向诱导渗透注浆。

4 饱和砂土定向诱导注浆试验及结果分析

4.1 试验设计

4.1.1 试验装置

试验模型箱采用有机玻璃制成，外加加固梁。注浆管和排水管均采用半径为3 cm且侧面开孔的有机玻璃管，孔隙水压力传感器采用规格为400 kPa的振弦式压力传感器，注浆泵采用QDX系列750C型潜水泵，排水泵采用QDX系列370C型潜水泵。试验模型如图5所示。

图5 饱和砂土定向诱导注浆试验模型

4.1.2 试验材料

饱和砂土定向诱导注浆试验主要采用石英砂作为多孔介质材料。由土质分析得到砂层粒径分布曲线，如图6所示。根据土质分析结果，试验所用砂层属于砾石，砂层渗透系数kw=8×10-2cm/s，土体颗粒的有效直径d=0.8 mm。

图6 试验砂土粒径分布曲线

试验注浆材料水灰比为1.0，浆液密度为ρg=1.52 g/cm3。水泥采用普通硅酸盐水泥(PC32.5R)。现场采用漏斗黏度计测量浆液漏斗黏度为14.62 s。根据文献[23]的研究结果可知，浆液漏斗黏度与浆液动力黏度换算关系为

(22)

式中A为浆液的漏斗黏度，s。

根据式(22)可得浆液动力黏度为11.56 mPa·s。

4.1.3 试验方法及数据采集

本文饱和砂土定向诱导注浆试验中，数据测量装置共设置5个土压力传感器、8个孔隙水压力传感器。所有传感器均为振弦式压力传感器，其布置于饱和砂土内部同一平面内，如图7所示。

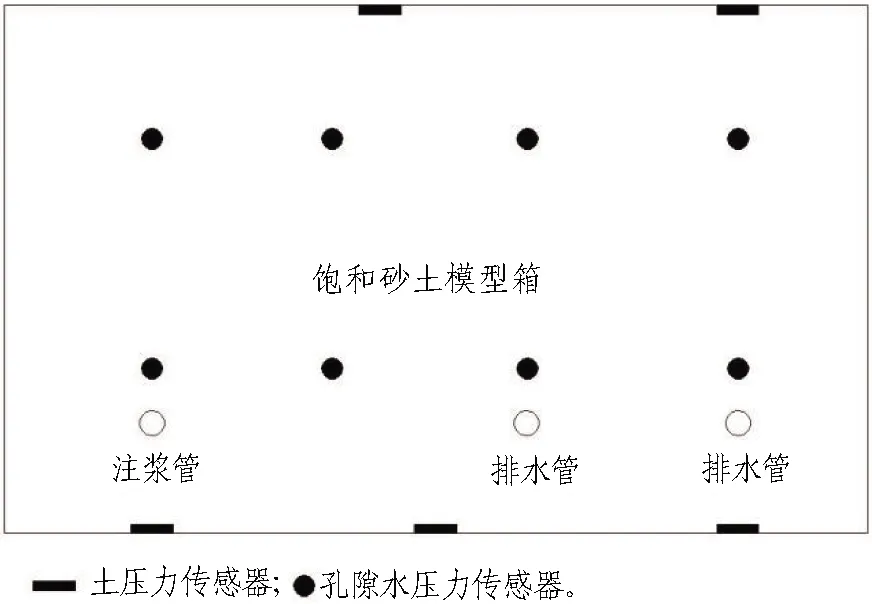
图7 试验传感器平面布置示意图

注浆过程中，各个传感器实际测量所得的数据为振弦频率，各个传感器的振弦频率与渗流压力变化值转换公式为

(23)

式中：p为传感器换算压力值，kPa；K为传感器率定系数，kPa/Hz2；f0为传感器初始频率，Hz；fi为传感器测量频率，Hz。

试验中各个传感器的数据采集频率为每5 s 1个，土压力传感器与孔隙水压力传感器测得的频率通过式(23)换算可得土压力与孔隙介质压力的变化值。

本文主要研究注浆管与排水管之间渗流压力梯度空间分布规律，故对以上试验模型进行简化，对相应的监测点进行编号。简化后试验模型的传感器监测点编号分别为DMKY-1、DMKY-2和DMKY-3，其平面布置示意如图8所示。本文饱和砂土定向诱导注浆试验采用振弦式孔隙水压力传感器测量试验过程中砂土中孔隙介质的压力变化值，其在一定程度上反映了注浆过程中的渗流压力梯度值。

图8 简化试验模型孔隙水压力传感器平面布置示意图

本文饱和砂土定向诱导注浆试验总共6组，第1组至第5组砂层采用均质石英砂，第6组采用河砂。本文采用前3组注浆试验数据对理论规律进行分析，3组试验的注浆设计参数见表2。试验过程中，注浆压力和排水压力均为恒压。

表2 注浆试验设计参数

根据以上试验设计参数，通过式(21)分别计算注浆过程中各监测点处浆液渗流雷诺数，计算结果见表3。

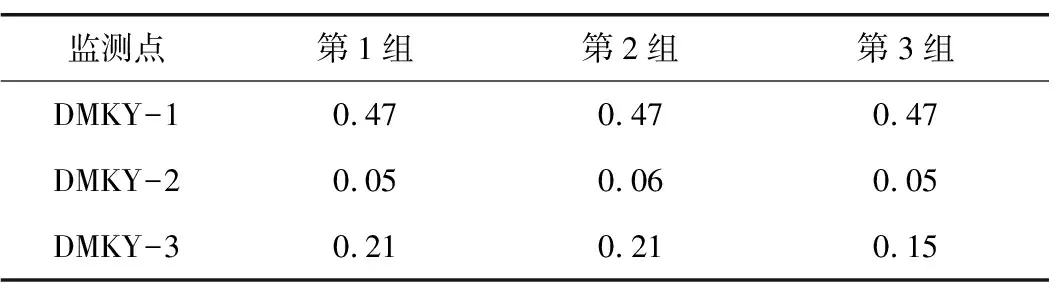
表3 注浆过程中各监测点处浆液渗流雷诺数

根据表3中雷诺数计算结果可知，浆液渗流符合达西定律使用条件，故满足本文公式适用性。

4.2 试验结果处理与分析

试验过程中的孔隙介质压力变化值反映了注浆过程中的渗流压力梯度。由于试验过程中存在大量的无效数据，因此本文对无效数据进行剔除，处理后每min数据量为7～9个，然后对每min的数据取平均值。根据注浆监测数据显示，注浆初始阶段由于饱和砂土中浆液与水不均匀分布，试验监测值波动较大。在注浆30 min之后3组试验的孔隙水压力传感器监测数据趋于稳定。此时，渗流压力梯度空间分布试验值与理论值对比如图9所示。

(a)第1组试验

由图9可知：

1)在一定误差允许范围内，本文推导的理论公式计算结果与试验结果一致性较好，本文理论公式可在一定程度上反映饱和承压水砂层在注浆压力与排水压力作用下排水诱导驱替注浆渗流压力梯度空间分布规律。

2)试验监测结果普遍大于本文推导的理论公式计算结果，理论值与试验值误差处于4.4%～29.0%。误差主要原因为试验过程中砂土的渗透系数和浆液黏度变化，导致试验监测值偏大。鉴于砂层注浆存在较大不确定性，误差处于可接受范围内。

3)试验初始注浆阶段，试验监测值波动幅度较大；浆液贯通渗流场后试验监测值逐渐趋于稳定；注浆结束后，在饱和砂层中可形成预期的定向加固区域。

5 工程应用分析

本文排水诱导驱替注浆技术主要为解决北京地铁17号线工程西坝河站—太阳宫站区间联络线段及渡线段饱和承压水砂层注浆加固问题。联络线段及渡线段开挖土层的饱和承压水砂层为中粗砂层，渗透系数kw=0.02 cm/s，浆液在饱和承压水砂层中的渗透系数kg=0.002 cm/s。工程施工中，注浆材料为水泥-水玻璃浆液，水泥浆的水灰比为1∶1，水泥浆与水玻璃体积比为1∶1，水玻璃溶液波美度为35 °Bé，双液浆的胶凝时间约为20 min，水泥-水玻璃浆液的屈服应力τ0取10 Pa。注浆过程中注浆泵压力值控制在300～800 kPa。由于饱和承压水砂层中承压水的影响，工程中渗透注浆半径取50 cm。

本文结合实际工程施工情况，对联络线段饱和承压水砂层采用排水诱导驱替注浆方法进行注浆加固，注浆过程中，在饱和承压水砂层一定范围内施加注浆压力与排水压力。工程施工中，抽水泵压力宜控制为200～400 kPa。根据以上参数，通过渗流压力梯度空间分布方程与启动梯度对最大管间距进行计算，计算结果如图10所示。

图10 不同初始注浆压力条件下最大管间距

根据计算结果可知，工程实际注浆条件下浆液扩散范围在54～105 cm。对于排水诱导驱替注浆方法而言，排水压力产生的抽吸力不仅减小了承压水的影响，而且对浆液渗流扩散提供了诱导作用。根据本文试验结果与工程施工经验可知，不同的注浆材料扩散效果与范围存在差异。因此，建议根据不同注浆材料合理选择管间距，以达到预期的定向注浆效果，当注浆材料为双液浆时，根据不同的工程地质砂层状况，注浆管与排水管间距建议控制在50～90 cm。

6 结论与讨论

1)本文依据达西定律与质量守恒定律建立了排水诱导驱替注浆相关理论，推导了在注浆压力和排水压力作用下排水诱导驱替注浆渗流压力梯度空间分布方程，通过饱和砂土定向诱导注浆试验得到了在注浆压力和排水压力作用下孔隙介质的压力变化规律，理论公式计算结果与试验结果的一致性较好。

2)本文理论计算结果与试验结果误差在4.4%～29.0%，误差处于可接受范围内。本文推导的理论公式基本符合饱和承压水砂层中注浆压力与排水压力作用下排水诱导驱替注浆渗流压力梯度空间分布规律。

3)饱和承压水砂层在排水诱导驱替注浆过程中，由于注浆压力与排水压力同时作用于渗流场，渗流压力梯度空间分布曲线在注浆管与排水管周围走势较陡，在渗流场中央走势较为平缓。渗流压力梯度空间分布曲线最低点大于启动梯度时，可实现定向诱导渗透注浆。实际工程注浆中，根据本文推导的理论公式可计算排水诱导驱替注浆的最大管间距及其相关注浆参数。

4)由于排水压力的诱导作用，浆液在注浆管与排水管之间可实现定向渗透扩散，在饱和承压水砂层内部形成预期的定向加固区域。本文根据现有的注浆施工经验与试验研究，建议当注浆材料为双液浆时排水诱导驱替注浆最大间距控制在50～90 cm。

5)通过本文推导的理论公式可确定注浆压力和排水压力作用下排水诱导驱替注浆渗流压力梯度的空间分布规律，并可分析工程应用中的相关参数，但对于注浆管与排水管之间的最大管间距与工程应用有待进一步深入研究。