合成地震动空间相干性的震源机制影响

万珂羽，孙晓丹，2

（1.西南交通大学土木工程学院，四川成都 610031；2.陆地交通地质灾害防治技术国家工程研究中心，四川成都 610031）

引言

我国是一个活断层广泛分布的国家，地震频率高、震级大，因此地震带来的危害不容忽视。当大长跨重大工程无法避开活断层时，则须从结构抗震角度对建筑进行必要的地震动输入［1］。在近断层范围内，空间两点地震动可能存在差异，这种地震动的空间差异对于大跨度建筑而言，可能导致结构各支承点的地震作用不相同，即，所谓的“多点激励”。平面尺寸较大的结构如核电站、大跨桥梁、坝体等，通常自振周期较长，地震反应与常见的工程结构物差别较大。早期受抗震设计理念和计算机能力的限制，对这类结构物的地震动输入仅考虑一致输入，即两支承点输入的地震波波形完全相同。而仅考虑简单的“一致激励”，会导致大跨度结构动力分析产生显著偏差［2］。赵大海等［3］针对大跨空间展览馆的研究表明，考虑多点激励后，结构的柱底剪力和弯矩、结构顶部的位移以及剪力墙的应力显著增大。吴祚菊等［4］以管道等长线结构为研究对象，发现在多点激励下，管道结构的环向切应力存在突变。复杂土体中的大型地下结构如隧道，在多点地震激励下，隧道截面各个部位间的相对位移也可能出现明显增大［5］。而若忽略地震动的空间差异，可能导致大跨拱桥内力的严重低估，甚至能引发高铁桥梁的落梁，造成危害［6，7］。

目前普遍认为，导致地震动空间差异的原因来自4种效应：1）行波效应（wave⁃passage effect）；2）不相干效应（incoherence effect）；3）衰减效应（attenuation effect）；4）局部场地效应（site⁃response effect）。但其中衰减效应对柔性较好的大跨结构影响较小［8］。Soyluk等［9，10］借助斜拉桥及上承式拱桥等大跨结构的地震响应分析，证明了不相干效应、局部场地效应与行波效应同等重要。王岱等［11］也通过均匀介质地下连续管线的地震响应，证实了局部场地效应、不相干效应的重要性。王燕丽［12］针对单层球面网壳，分析了行波效应、不相干效应以及两种效应耦合的激励方式，分析表明同时考虑两种效应耦合时对结构影响最大。

为了研究空间两点地震动的相干性特征，一些国家建立了密集观测台阵，如我国台湾布设的SMART-1（Strong Motion Array in Taiwan，phase I）大型台阵。基于密集台阵记录，利用随机信号处理中的相干函数（co⁃herence function）进行统计分析，以此描述地震动相干性的变化特征和影响规律。目前普遍认为，地震动空间相干性随两点间间距增加而降低，随频率的增加而降低。此外，王国新等［13］发现地震动相干性随深度增加也呈现降低趋势。而地震动竖向分量的相干函数变化规律与水平分量相似，相干性随频率增大而减小，随两点间距离增大而减小［14］。三个地震动平动分量间是低相干的。水平分量与垂直分量间的相干性小于两水平分量间的相干性，同测点不同地震动分量间的相干性随频率衰减不明显［15］。为了构建地震动空间场，20世纪80年代起，建立了许多相干函数模型，分为理论相干函数模型［16-19］与经验相干函数模型［20-26］，其中应用较为广泛的是Abarahamson（1991）的模型和Loh（1990）的模型。

但大部分相干函数模型，都是基于实测的密集台阵记录统计得到的，严格地说其结论只适于该台阵场地类型。但是，地震动的空间差异受震源、传播途径、场地条件等多种因素的影响，特别是在震源效应显著的近断层区域，地震动的空间变化更为复杂［27］。但是，大震近场地震动记录还不够丰富。若采用实测记录进行相干性分布的计算，不仅受场地条件等影响，还缺少精确的震源机制信息，因此借助合成的地震动场研究空间相干性，是一种有效的手段。如，丁海平等［28，29］基于合成的地震动场，提出了基岩地震动相干函数模型，并分析了走滑断层与倾滑断层的不同震源机制影响。路建波等［30］也利用震源—传播途径—场地条件一体化的地震动模拟方法，合成了设定地震的地震动场，分析了相干系数的变化规律，认为基于合成地震动得到的相干函数特征与基于密集台阵数据的相干函数特征基本相符。郑飞和叶继红［31］借助均匀单一介质理论地震图，研究了地震动相干性，并认为地震动相干性随地震波的传播方向存在各向异性，断层走向是空间地震动场相干性的重要影响因素。

总的来说，目前绝大部分相干函数研究中，震源机制的考虑仍不多见。因此，本文借助近场地震动的运动学模拟方法，计算不同设定断层引起的空间地震动场，探究空间相干性受震源机制变化的特征规律。

1 近场地震动的运动学模拟

根据Hartzell等［32］提出的地震动模拟的运动学模型，设定地震引起的某点在某时刻的地震动位移U（x，t），可以通过给定速度结构下理论格林函数的叠加实现：

该方法中，假定断层面上分布着不同尺寸的许多子震，每个子震视为具有等效半径的独立地震。子震的分布互不重叠，子震的尺寸符合2的幂次分形，且符合ω-2高频谱衰减。最小子震的震源时间函数采用Brune模型R（t）=te-λt［33-35］；最小子震的拐角频率为f0smallest=4.9×106×β（Δσ/M0smallest）1/3，β是震源区剪切波速。通过叠加最小子震并与标度因子-S(f)=C[1+(f/f0smallest)2]/[1+(f/f0larger)2]卷积可以构建更大规模的子震，其中(f)是公式（1）中S(t)的傅里叶变换；C可以保证叠加的子震的总地震矩等于目标地震矩。公式（1）中，g（x，y，t-tsij-trij）是最小子震引起的地震动位移，采用成层半空间全波理论波数法计算［36］；Nk是第jk个子震的断层面积中包含的最小子震的个数；*代表卷积；tsij、trij分别代表了S波从第i个子震传播到场点引起的时间延迟以及破裂从起始点扩展到第i个子震的破裂时间延迟；r0/rij项表达的是几何传播效应，其中rij是子震至台站x的距离，而r0是g（x，y，t）i j中震源y至台站x的距离；借助Δσij/Δσ0可以实现非均匀滑动分布的表达，其中应力降代表的是根据子断层滑动量累积计算出的静应力降［37，38］。不过，本文中为突出震源机制对空间相干性的影响，排除断层滑动分布的干扰，采用了均匀滑动分布假设。公式（1）中的叠加包括3个过程：首先，叠加最小子震形成每一个尺寸为k的子震，然后叠加全部尺寸为k的子震，最后把L个不同尺寸的所有子震叠加起来，形成最终的地震动时程。

本文采用非线性土层校正程序DESA2表达近地表土层效应，假定场地为美国NEHRP场地分类为C类［39，40］。本文假定目标场地位于四川省，借助九寨沟地区地壳构造信息，构建了25层的水平成层速度结构模型。速度结构中包含了高速-低速层（图1），高-低速层相间的平层波导能够实现区域的地震波衰减效应模拟［41］。滞弹性衰减模型［42］为Qp=300f0.5和Qs=150f0.5。

图1 四川地区设定工程场地一维速度结构模型Fig.1 One-dimensional velocity structure model of engineering site in Sichuan

图2是水平成层场地的断层破裂面示意图。其中断层长度L=15 km，断层宽度W=10 km，震源深度H=20 km，A点为断层起始破裂点，在地表的投影与C00点重合。地震波传播方向为双向传播，滑动面模型沿走向和倾向离散成13×9=117个子源。

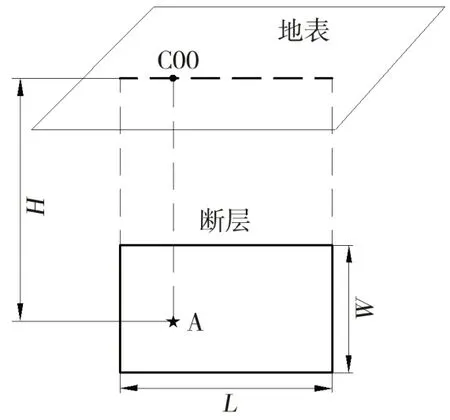
图2 断层计算模型Fig.2 The calculation model of fault

本文依照密集观测台阵的形式设置计算场点，构建模拟台站，如图3所示。模拟台阵以C00为中心计算点，环状布置24个台站，从内向外共计3圈，半径分别是200 m、600 m、1 000 m。每圈上布置8个台站，分别位于正东、正西、正南、正北、东北、东南、西北、西南8个方向上。半径为200 m的计算点称为内圈计算点，从正北方向出发顺时针编号I01、I02、……I08；同理，半径为600 m的计算点称为中圈计算点，以M开头顺时针编号；半径为1 000 m的计算点为外圈计算点，以O开头顺时针编号。在模拟中断层的走向、倾角、滑动角随不同工况有所变化，图4中所示的就是走向为153°，倾角为84°，滑动角为-33°时的部分计算点EW方向的地震动时程。在做相干函数计算之前，先将合成的地震动时程旋转成为平行断层与垂直断层两条地震动分量，以进一步观察空间相干性与断层方位之间的关系。

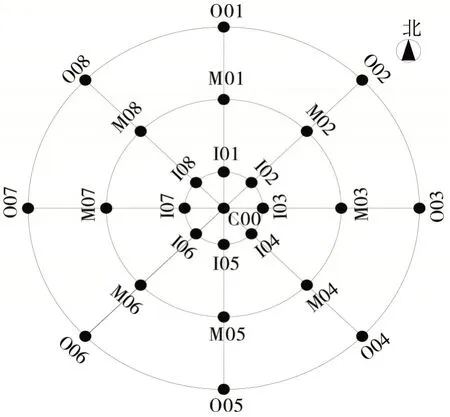
图3 模拟台阵布局Fig.3 Simulated dense array configuration

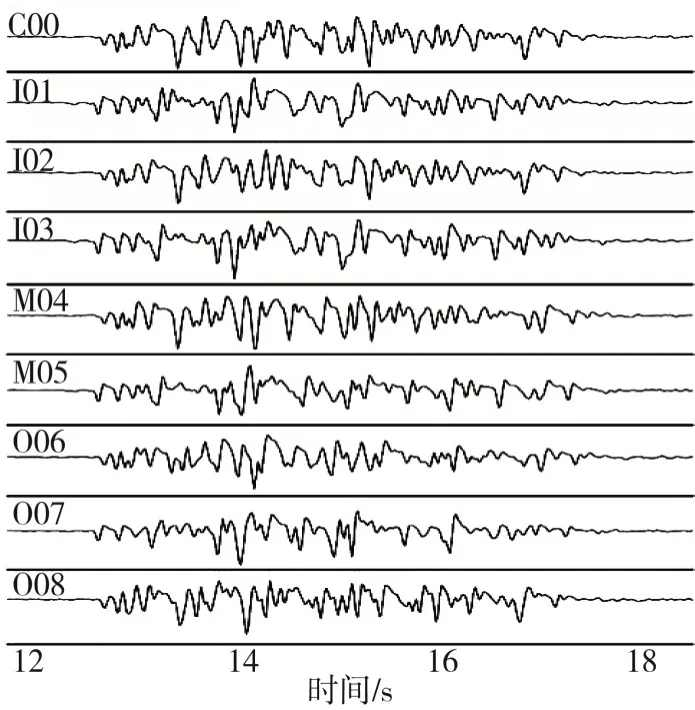
图4 走向153°倾角84°滑动角-33°部分EW向加速度时程图Fig.4 Partial EW accelerations for strike 153°，dip 84°，rake-33°

2 相干函数的计算

对于两个计算点i和j，相干函数γij(ω)的模为：

为做对比本文进而采用Loh（1990）相干函数模型对相干系数曲线进行拟合：

式中，ω=2πf，d为两点间间距。得到的拟合模型曲线如图5中虚线所示。下文中在地震动模拟中依次变换断层的走向、倾角和滑动角，并将得到的相干系数曲线按公式（3）拟合后，进行对比。

图5 走向153°倾角84°滑动角-33°时EW分量相干函数计算及拟合图Fig.5 Calculated and fitted coherence for EW component for strike 153°，dip 84°，rake-33°

3 震源机制对相干性的影响

3.1 断层走向对相干性的影响

本文首先探讨断层走向变化对空间相干性的影响。假定断层倾角为45°、滑动角0°保持不变，分别取断层走向为45°、135°、225°和315°。模拟各断层走向情况下，25个模拟台站处的地震动时程，并计算各台站与中心台站之间的相干系数曲线。图6和图7分别给出了平行断层分量与垂直断层分量的相干系数。受篇幅限制，图中只列出了45°、135°、225°和315°方向上点对（即后缀02、04、06和08的点与中心点之间）的相干系数曲线。图6和图7中，不同颜色表示不同的点距情况，其中黑色、蓝色、红色分别代表点距200 m、600 m、1 000 m时相干系数曲线变化情况；不同的线型又表示不同的断层走向情况。

首先观察不同颜色的曲线之间的差异。由图6和图7可见，相干系数随点对距离增加普遍降低，且随着频率增加，下降的幅度越大。此外，可以观察到的一个明显规律是，于平行断层分量而言，相干系数曲线在2 Hz以下频段随着距离增加而下降的幅度不明显。对于垂直断层分量，点距从600 m增至1 000 m时，相干系数在2 Hz以下频段显著下降。

再观察不同线型的曲线差异。图6和图7中显示，当计算点距离中心点200 m时，断层走向的变化对于相干性几乎不存在影响。当计算点距离中心点600 m以上时，断层走向变化可导致垂直断层分量的相干系数曲线产生差异，且频率越大差异越大，点距1 000 m时这种差异更为显著。一个有趣的规律是，对于平行断层的分量来说，走向对相干性的影响并不显著，但仍存在沿断层走向方向的点对在2 Hz以下频段相干系数较低的规律。对于垂直断层分量来说，相干性分布情况存在显著差异，断层走向与点对方向平行时，相干系数明显低于断层走向与点对方向垂直的情况。

图6 走向为45°、135°、225°以及315°时，倾角45°，滑动角0°平行断层分量相干函数图Fig.6 Coherence of parallel fault component of simulated ground motion for dip 45°and rake 0°with the variable strike of 45°，135°，225°and 315°

图7 走向为45°、135°、225°以及315°时，倾角45°，滑动角0°垂直断层分量相干函数图Fig.7 Coherence of perpendicular fault component of simulated ground motion for dip 45°and rake 0°with the variable strike of 45°，135°，225°and 315°

3.2 断层倾角对相干性的影响

接下来探讨断层倾角变化对空间相干性的影响。假定断层走向为45°、滑动角0°保持不变，依次取断层倾角为15°、45°和75°。分别模拟各断层倾角情况下，25个模拟台站处的地震动时程，并计算各台站与中心台站之间的相干系数曲线。图8和图9分别给出了平行断层分量和垂直断层分量的相干系数，不同颜色表示不同的点距情况，其中黑色、蓝色、红色分别代表点距200 m、600 m、1 000 m时相干系数曲线变化情况；不同的线型又表示不同的断层倾角情况。受篇幅限制，仍只显示45°、135°、225°和315°方向上点对的相干系数曲线。

图8 倾角为15°，45°以及75°时，走向45°，滑动角0°平行断层分量相干函数图Fig.8 Coherence of parallel fault component of simulated ground motion for strike 45°and rake 0°with the variable dip of 15°，45°，and 75°

图9 倾角为15°，45°以及75°时，走向45°，滑动角0°垂直断层分量相干函数图Fig.9 Coherence of perpendicular fault component of simulated ground motion for strike 45°and rake 0°with the variable dip of 15°，45°，and 75°

在图8与图9中，先观察不同颜色的曲线簇给出的差异，可看出各方向点对的相干系数随距离的增加均呈现下降趋势，且随着频率的增加，下降的幅度越大。值得注意的是，于平行断层分量而言，沿走向方向的点对引起的相干性在2 Hz以下频段随距离的增加无显著下降。而对于垂直断层分量，平行断层走向的点对给出的相干系数衰减速率大于垂直断层走向的点对。

再由不同曲线线型探讨断层倾角对相干性的影响。由图8和图9可见，点距200 m时，倾角的变化对平行断层分量的影响并不明显，仅在沿走向方向上的相干性随着倾角的增加缓慢降低。有趣的是，随着点距的增加，倾角对相干性的影响逐渐显现。进一步可观察到，在垂直断层迹线的方向上，平行断层分量与垂直断层分量给出的相干性均表现出随倾角减小而衰减的性质。

3.3 断层滑动角对相干性的影响

随后，本文探讨滑动角变化对空间相干性的影响。假定断层走向为45°、倾角为45°保持不变，分别取滑动角为0°、180°、90°和-90°。分别模拟各滑动角情况下，25个模拟台站处的地震动时程，并计算各台站与中心台站之间的相干系数曲线。图10和图11分别给出了平行断层分量和垂直断层分量的相干系数，不同颜色表示不同的点距情况，其中黑色、蓝色、红色分别代表点距200 m、600 m、1000 m时相干系数曲线变化情况；不同的线型又表示不同的断层滑动角情况。仍只针对45°、135°、225°和315°方向上点对的相干系数曲线进行分析。由图10和图11可见，滑动角为0°和180°时（即，左旋走滑与右旋走滑）相干系数曲线完全重合，滑动角为90°和-90°时（即，正断层与逆断层）相干系数曲线完全重合，所以，将四种滑动角合并为走滑断层与倾滑断层两种情况进行分析。

先观察不同颜色曲线簇之间的差异。图10与图11展示了走滑和倾滑2种情况下，各方向点对的相干系数随距离变化的情况。从图中可以观察到，无论走滑还是倾滑运动模式，相干系数随着点对距离的增加，都是下降的。相干系数随频率变化的下降速率和幅度是基本相同的。同时可以观察到，走滑断层模式下，平行断层分量给出的相干系数在2 Hz以下随距离的增加无明显下降。此外，当点距1 000 m时，垂直断层分量的相干系数在低频处的衰减大于平行断层分量的情况。

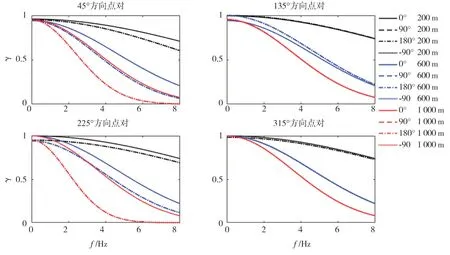
图10 滑动角为0°，90°，180°以及-90°时，走向45°，倾角45°平行断层分量相干函数图Fig.10 Coherence of parallel fault component of simulated ground motion for strike 45°and dip 45°with the variable rake of 0°，90°，180°and-90°

再观察曲线不同线型之间的差异。从图10和图11可以共同观察到，对于平行断层分量和垂直断层分量来说，点距200 m时走滑或倾滑运动模式对于相干系数几乎不存在影响。随着点距的增加，滑动方向的影响逐渐表现出来。但这种影响对于平行断层走向方向的点对而言，则更为显著，而对于垂直断层走向方向的点对来说，仅出现了细微的空间差异性。进一步发现，在平行走向方向的点对上，对于平行断层分量来说，倾滑断层给出的相干系数曲线要低于走滑断层给出的相干系数曲线，而对于垂直断层分量来说，则正相反，走滑断层给出的相干系数曲线相对更低。

图11 滑动角为0°，90°，180°以及-90°时，走向45°，倾角45°垂直断层分量相干函数图Fig.11 Coherence of perpendicular fault component of simulated ground motion for strike 45°and dip 45°with the variable rake of 0°，90°，180°and-90°

4 结论

本文借助地震动的运动学模拟方法，对四川某设定工程场地的地震动场进行模拟。在模拟中，变换断层的走向、倾角以及滑动角，计算设定环形台阵上各点相干系数，分析了走向、倾角以及滑动角对地震动场空间相干性的影响。研究得到的主要结论包括：

合成地震动场的相干系数，表现出了明显的随两点间距离、频率的增加而降低的特征，这与目前地震动空间相干性的普遍认识相符，表明用合成的地震动场研究空间相干性是可靠的。

断层走向的变化，对地震动场空间相干性的影响比较显著，这与郑飞和叶继红（2009）认为的断层走向是空间地震动场相干性的重要影响因素的结论吻合。且断层走向对空间相干性的影响规律性比较明显。即，对于平行断层分量来说，沿断层走向方位的空间相干性在2 Hz以下频段较低。对于垂直断层分量来说，平行于断层走向的区域相干性明显低于垂直断层走向的区域。

断层倾角变化，对地震动场空间相干性也有较大影响。表现为，两个水平分量给的空间相干性均在垂直断层走向的区域表现出随倾角的增大而显著增加的规律。

滑动角的变化，对地震动场空间相干性的影响也较为显著，且具有明显规律性。体现在，对于平行断层分量来说，倾滑断层给出的相干性要低于走滑断层给出的相干性，且在平行断层走向方向上相干性随距离增加快速下降；对于垂直断层分量来说，走滑断层反而给出了更低的相干性，且在平行断层走向的方向上相干性随距离增加快速下降。

在模拟地震动的过程中将断层的滑动面设置为均匀分布，有效避免了其他因素的干扰，以突出震源机制参数对空间相干性的影响。且，研究结果中出现了左旋走滑与右旋走滑相干性完全相同以及正断层与逆断层相干性完全相同的特征，是因为滑动角改变180°时，不影响断层面的力学性质，仅使得相应台站的加速度记录方向相反，因此并未影响相干系数计算结果。此外，本文为排除局部场地条件的影响，在地震动合成中采用了水平成层速度结构模型。对于横向不均匀介质场地来说，地震动空间相干性变化特征更为复杂。今后可基于三维不均匀介质模型合成地震动场，与本文对比探讨局部场地条件对空间相干性的影响规律。