建筑运维阶段可接受风险标准及基于LQI的最优安全投资方案研究
2022-03-10张子墨陈思佳
张子墨,陈思佳,张 辉
(1.上海交通大学船舶与海洋建筑工程学院,上海 200240;2.上海建科工程咨询有限公司上海市工程结构安全重点实验室,上海 200032)
引言
近年来我国经济迅猛发展,其中建筑行业的总产值也不断增加。建筑在建设完成后开始投入使用,并进入长期运行维护阶段,期间的各种安全事故也在逐年增加。目前国内外研究学者对于建筑风险的研究主要集中在施工阶段,针对建筑运维阶段的风险研究较少,正处于起步阶段[1]。
风险在不同领域有着不同的表现形式,对“风险”的探讨也已经有很多[2,3]。但不论如何定义风险,在主观上,建筑运维阶段的所有利益相关者(包括政府、业主、使用人员、维护人员等)都不希望存在风险。此时,为了利用合理的资源最大程度地降低风险,基于广泛认同的价值观和原则而建立的定量分析方法是必要的,它可以帮助决策者在面对复杂问题时根据数据做出判断,回答“怎样的安全是安全”的问题[4]。为了实现这一目标,通常的方法是将风险限制在一个合理的、可接受的水平上,并基于影响风险的各种因素,建立合适的风险评估模型,寻求最佳的安全投资方案。
现阶段关于风险可接受性,在其他工程领域的学者也已做了大量研究。1974年英国健康和安全委员会(theHealth and Safety Executive,HSE)[5]提出了著名的“在可行的范围内尽量低(As Low As Reasonable Practi⁃cable,ALARP)”风险评价准则;尚志海等[6]系统阐述了可接受风险的定义与研究方法。很多学者也给出了不同领域的可接受风险标准,赵成等[7]使用历史统计法给出了住宅火灾个人风险可接受标准值;张舒等[8]采用AIR值法计算出煤矿个人可接受风险标准值;针对我国大坝可接受风险标准,周兴波等[9]也进行了深入研究并给出了相应的社会可接受风险标准值。同时在泥石流灾害风险[10]、油气管道风险[11]、病险水库风险[12]等研究领域,也都有相关学者对基于LQI理论而建立的最优安全投资方案的研究。
目前在建筑运维阶段,我国在该领域既没有制定明确的可接受风险标准,同时也缺少围绕可接受风险标准而建立的最优安全投资方案。因此,本文将综合考虑其他工程领域对于可接受风险标准的规定及其研究方法并与建筑运维阶段的实际情况相结合,确定在建筑运维阶段的可接受风险标准,同时将基于改进生活质量指数,量化控制风险所需投资,建立一个合理的最优安全投资方案。
1 建筑运维阶段可接受风险标准
基于2009年,联合国国际减灾战略组织(UNISDR)[13]对可接受风险的定义,可以给出建筑运维阶段的可接受风险定义:在现有社会、经济、政治和环境条件下,各利益相关者可以接受建筑破坏导致的潜在损失。
1.1 建筑运维阶段的风险分级原则及研究方法确定
建筑运维阶段可接受风险标准的制定,需要综合考虑到目前的技术水平、社会制度、法律法规、经济发展水平、环境保护以及公众心理承受能力等因素,确定社会各方都能接受的风险界限。吕保和等[14]在“可接受风险标准研究现状与思考”中提出了在制定我国可接受风险标准时应遵循的若干原则。本文结合相关领域学者的研究成果,提出建筑运维阶段可接受风险标准制定所需满足的原则:
(1)平等原则:风险面前人人平等。对任何人而言,生命都是最宝贵的,因此不能把任何人暴露在较大风险之下,必须设定一个人类所能承受的最大风险限值,超过这一限值,应无条件采取措施降低风险。
(2)利益相关者可接受原则[15]:风险可接受性的问题涉及科学、技术、社会等多个领域,因此建筑运维阶段可接受风险标准的制定,也应该以多个角度出发,最大程度保证利益相关者都能接受。
(3)同等风险水平原则:结合Jonkman等[16]相关研究,借鉴GAMAB原则[17],制定的建筑运维阶段的可接受风险水平至少达到目前全球相关领域的风险等级。
(4)动态原则:随着经济社会发展、安全生产环境改善、人们思想观念变化,公众的风险可接受标准也应该动态变化。其在短期内作为标准应具有时效性,长期看也要体现出动态变化的特征。
考虑到建筑运维阶段的风险影响是多方面的,本文对它的研究将从生命风险(包括个人风险、社会风险)、经济风险、环境风险以及社会稳定风险这4个方面展开。现阶段国内外针对可接受风险标准的研究方法有多种,主要分为主观调查法与客观度量法。本文采用客观法中的横向对比法,这种方法最为直接,通过对相关领域的可接受风险标准进行横向对比,从而确定建筑运维阶段的可接受风险标准。
1.2 个人可接受风险
现阶段国内外机构或学者针对个人可接受风险标准提出了很多建议。1992年,英国健康和安全委员[18]建议主要工业灾害的典型个体可接受风险值取10-6~10-5/年;李剑锋等[19]给出我国个人风险值(Individual Risk,IR)区间为1.89×10-7~9.43×10-6/年;杜效鹄等[20]提出我国大坝溃坝个人可容忍风险标准不应低于10-4/年,可接受风险标准不低于10-5/年;周兴波等[9]认为我国大坝生命可接受风险研究领域,设定为10-5/年为可接受风险标准是合理的。更多国内外不同行业的个人可接受风险标准如表1所示。

表1 国内外部分行业个人可接受风险标准Table 1 Part of the individual risk criteria at home and abroad
参考目前国内外各行业的个人风险标准,综合考虑我国社会经济的发展水平以及人口大国这一国情,按照死亡率同等风险水平原则,建议建筑运维阶段的个人生命可容忍风险标准为10-5/年,可接受风险标准为10-6/年。
1.3 社会可接受风险
建筑运维阶段的社会生命风险标准可以参考目前大部分文献的表达方法,即通过FN曲线来表达。绘制FN曲线的关键是确定其斜率n,截距C以及后果限制值。于汐等[15]在重大岩土工程可接受风险标准研究中对此有细致的讨论,并建议斜率n取-1,可容忍风险曲线截距取10-3/年,可接受风险曲线截距取10-4/年,可容忍后果限制值取1 000人,可接受后果限制值取100人。国内在相关领域研究社会可接受风险标准的学者建议的FN曲线斜率也多为-1[24,25]。
对于截距C的取值,赵新伟等[26]建议中国油气管道FN曲线的可容忍风险标准截距取10-4/年。李雷等[27]给出大中型水库FN线起点为10-3/年,可容忍和可接受FN的极限值分别为10-5/年和10-6/年。
当死亡人数超出一定限度,不论怎样低的可接受风险标准值都是不可接受的社会风险,因此要设定一个后果限制值。国内学者周兴波等[9]建议我国大坝以年计的社会可容忍风险标准以1 000人为后果限制值;李红英等[25]建议库区滑坡灾害以1 000人为后果限制值。我国《生产安全事故报告和调查处理条例》中规定死亡人数为30人以上的事件称为特别重大事故;造成3人以下死亡的称为一般事故。
综上,建议我国建筑运维阶段的FN曲线参数如下,取斜率n为-1,可容忍风险标准截距取10-3/年,可接受风险标准截距取10-4/年,可容忍后果限制值为30人,可接受后果限制值为3人。依此绘制建筑运维阶段社会生命可接受风险标准FN曲线,如图1所示。
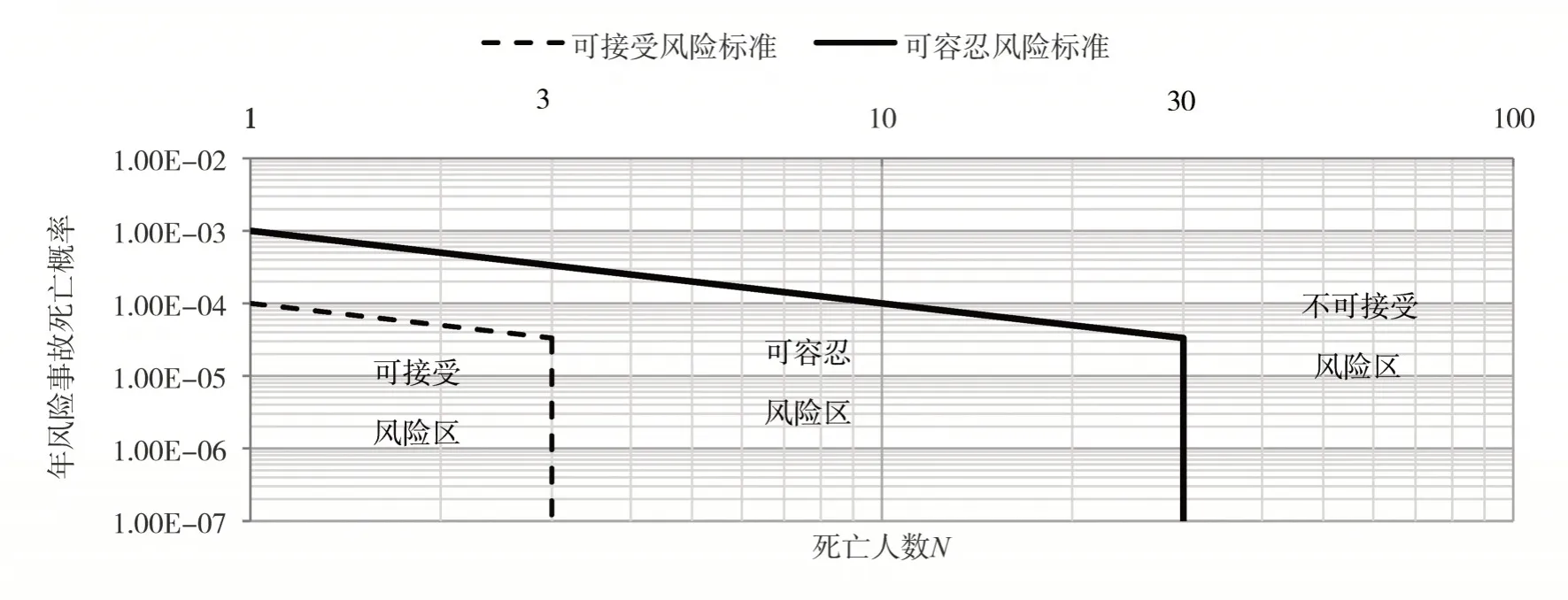
图1 建筑运维阶段社会可接受风险FN曲线Fig.1 Social life acceptable risk criteria FN curve for building operation and maintenance stage
1.4 经济可接受风险
目前国内对于建筑运维阶段的经济可接受风险标准研究并未有明确的文献资料,在其他相关领域中经济可接受风险标准通常采用FD曲线来表达。我国的《生产安全事故报告和调查处理条例》中规定,造成1亿元以上直接经济损失的事故称为特别重大事故,1 000万元以下直接经济损失的事故称为一般事故,类比前文FN曲线参数取值,以及国内相关领域学者于汐[15]、李雷[27]、秦国晋[28]等在该方向的研究成果。
本文建议建筑运维阶段的经济可接受风险标准中FD曲线的斜率n取-1,可容忍风险标准值截距为10-3,将108元作为可容忍风险后果限制值;设置可接受风险标准值截距为10-4,将107元作为可接受风险后果限制值。
1.5 环境以及社会稳定可接受风险
目前国内外的环境可接受风险标准研究大多在极易引起环境污染的领域,且针对区域突发性环境污染事件可接受风险的研究较少[29]。因此本文建议在建筑运维阶段的环境可接受风险标准可暂时参考挪威技术标准协会[30]提出的环境污染可接受风险标准。
社会稳定可接受风险的确定可以依据由中国国家发展与改革委员会(2012)出台的《国家发展改革委重大固定资产投资项目社会稳定风险评估暂行办法》。
王力等[31]在重大水利枢纽工程社会稳定风险研究中,采用未确知测度理论(Uncertainty Measurement,UM)构建社会稳定风险等级评估模型。之后的研究人员亦可借鉴此方法细化建筑运维阶段的社会稳定风险标准,并继续深入研究建筑运维阶段在生命、经济、环境等方面更合理准确的风险评价标准,在这一领域作出新的贡献。
前文详述的可接受风险标准中,生命风险(个人或社会)和经济风险是最直观的,其中生命风险是事故中公众关注度最高、也是决策者最想减少的。本文采用生命风险作为建筑运维阶段的主要风险分级标准,并选择个人可接受风险标准值作为最优安全投资的目标,展开基于LQI的最优安全投资方案的研究。
2 基于LQI的风险评价标准建立
生命质量指数(Life Quality Index⁃LQI)是由Pandey、Lind等[32]最先提出,起初应用于公共管理领域,近些年来逐渐成为众多学者评估涉及工程领域生命安全的风险控制决策工具,并形成了较多研究成果。
Pandey等将LQI应用于空气污染等公共安全领域,给出了基于LQI理论的决策应用方法;Rackwitz等[33]将LQI应用于结构可靠度的研究,推动了LQI在结构可靠度领域的应用;国内学者关贤军等[34]也基于LQI理论进一步完善了我国在结构目标可靠度领域的研究;尚志海等[10]基于LQI给出了在泥石流灾害领域的生命风险价值评估方法;胡江等[12]研究了基于LQI的病险水库除险加固效应评价方法;张舒等[8]在研究我国煤矿可接受风险标准中引入了LQI,并基于LQI计算了我国煤矿可接受风险标准的最优安全投资;吕大刚等[35]将LQI应用于地震灾害的生命损失估计中,给出了相应的社会挽救生命成本;于汐等[15]利用LQI提出了在重大岩土工程领域降低风险的最优化投资方法;赵成等[7]将LQI应用于住宅火灾可接受风险标准研究,给出了住宅火灾风险中的最优投入成本。
本文将在LQI理论基础上,结合已有的研究成果,建立适合于建筑运维阶段风险的最优安全投资方案。
2.1 生活质量指数LQI的公式及其改进
由生活质量指数的定义可知其表达式为

式中:g表示人均国民生产力;e表示出生时人口的预期寿命;w表示工作时间占预期寿命的比例,称为“工作时间比”。
从经济学的角度考虑前文的LQI表达式,对于财富或GDP来说,劳动(LQI中的工作时间)是非常重要的部分,但是还有一部分的GDP来自于资产或者说来自于投资。所以对于LQI来说,影响其中的财富增长的部分还应包括投资所得,这部分并非因为劳动所得。对此,国际标准ISO2394:2015[36]引入了柯布—道格拉斯弹性系数,并给出了改进的生活质量指数表达式

式中:q=w/[β(1-w)],β称为“柯布—道格拉斯弹性系数”,即休闲时间中投资带来财富的影响。
引入柯布—道格拉斯弹性系数后,式(1)可改进为

显然,考虑了休闲时间中投资对经济生产的影响的公式更具普适性和合理性。
对LQI的改进公式(3)两边求导并除以L可得

式中:dL是LQI的增量,dg是人均GDP的增量,而d e是预期寿命的变化。
当dL<0,表示生活质量指数在降低,这种情况说明风险管理措施不当,违背了公共利益,不能被社会接受;当dL>0时,说明国内生产总值用于保护生命的投资过于安全,造成资金浪费,但是可接受;当dL=0时,国内生产总值用于保护生命安全的投资则是无多余浪费的最优方案,此时的投资也是社会愿意支付的保护生命成本。
令dL/L=0时,可以得到

上式表达了人均国内生产总值的降低(d g为负),将带来预期寿命的增加(d e为正)。
对式(5)两边分别从g到g+Δg积分,e到e+Δe积分可以得到

经过移项,从而可得每年延长一个人Δe年的寿命的费用,以ΔC表示为

上式ΔC即为每年的最优安全投资成本,从上述的定义和积分过程可以发现,该成本是每年延长一个人Δe年寿命的费用。
2.2 基于改进LQI的避免死亡隐含费用ICAF
在灾害经济学和保险学中,一般利用“避免死亡隐含费用(Implied Cost of Averting a Fatality,ICAF)”作为在灾难事件中付给受害者经济补偿的数量指标,类似于补偿给受害者的保险费用[33]。那么对于某项安全措施的ICAF值来说,则是从决策时刻开始,要避免一个人的死亡,即需要延长该人Δe年寿命到达预期寿命的费用,对此每年需投入的资金为:

上式可以认为是某项安全措施为了拯救一个人所需要投入的合理资源。当然,这里需要强调的是,ICAF值不能看作是人的生命价值,因为生命无价,而且衡量生命价值这件事情本身就是不道德的,ICAF值所度量的是社会所能负担的并且应当以道德原则所支付的保护生命的费用。
在建筑运维阶段风险中,更直观的数据应是处在风险中社会群体的社会挽救费用(SLSC),其计算公式为:

式中:F为实际死亡率,F a为可接受死亡率,N p为对应社会群体的人口总数。
2.3 ICAF的影响因素及在本文中的考虑
对不同地区、不同行业、不同工作内容、不同年龄段的社会群体而言,其各自的w、β、Δe取值都会有所不同,有必要对这些数值的选取进行分析讨论。
2.3.1w的影响
前文的LQI表达式中w被认为是一个人工作时间占其生命总时间的比例,则(1-w)是剩余的非工作时间或休闲时间。那么假设每天工作时间为8小时,每周工作5天,每年法定假日11天,所以每年工作天数为

则每年的工作时间为

若假定我国一个人的平均工作时间为a年,则一个人一生总共的工作时间为

假设预期寿命为e,则工作时间的比例w为

而Ditlevsen等[37]则对休闲时间即(1-w)提出了不同的看法,他们认为LQI中(1-w)的部分并非仅仅是一个人对GDP没有贡献的时间,而应该是享受健康生活和娱乐的时间,那才是人们的追求。其中的睡眠时间是保证人身体健康、保持清醒从而享受生活和正常工作所必须的时间,它不应该被算在(1-w)里面,即享受生活的时间应扣除正常的睡眠时间。
如果认为正常睡眠时间为8小时,则上述工作时间的比例w为

如果考虑到我国不同行业的实际工作时间,假设每天工作时间为t1,每周工作d1天,每年除周末外的其他假期为d2天,则按照上述计算过程可得w为
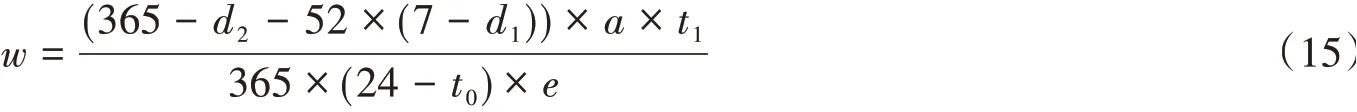
全国劳动者的平均工作时间比例可以按照式(13)计算。根据调查数据显示,中国2019年平均寿命达到了77岁。国家法定的企业职工退休年龄是男人年满60周岁,女工人年满50周岁,女干部年满55周岁。鉴于这一退休年龄有延迟的趋势,可以选取40年为劳动者的平均工作年限,则工作时间比例为

在建筑运维阶段的风险研究中,w值可以结合当地的平均年龄和平均工作时间依据公式进行计算。
2.3.2β的影响
对于柯布—道格拉斯弹性系数的取值,国际上在经济学领域一般取β=0.6~0.8,我国国家计委针对我国国情经过计算给出的结果为β=0.7~0.8。这些值是适合国家宏观经济领域的,可作为参考。对于LQI中β的取值,新版ISO2394-2015结构可靠度标准中的建议是取β=0.7。苏黎世大学的Faber等[38]经过研究给出的建议是,对于发达国家取β=0.7,发展中国家取β=0.6。国内大部分工程领域的学者在利用LQI进行最优安全投入成本研究时,并未引入β参数,即默认取β=1进行计算。吕大刚等[35]将LQI应用于地震生命损失估计时,考虑了β的影响,并结合我国实际工作情况建议β=0.7。
综上所述,引入柯布—道格拉斯弹性系数到LQI理论中是较为需要和可行的。根据目前的文献成果,综合考虑各方机构以及学者对β的取值,本文建议在建筑运维阶段,β取0.7。
2.3.3 Δe的影响
对于Δe的取值,国内部分学者李静等[11]、吕大刚等[35]采用人口年龄分布密度曲线的积分结果来表达人们期望延长的寿命。吕大刚等通过调研数据并计算发现,在社会群体中,ICAF的计算结果相当于避免一名中年人死亡的费用,即Δe=e/2,代入可得ICAF的一个实用表达式为

这个Δe的近似取值也被国内众多学者所认同。因此,本文建议在建筑运维阶段风险研究领域一般情况下Δe取值为0.5e;在平均年龄较低地区中Δe取值为0.6e;平均年龄较高地区中Δe取值为0.4e。
2.3.4 各省市ICAF值计算对比
查询2019年各省市统计局统计的国内生产总值数据、人口数量、期望寿命等数据,并基于此计算各省市的ICAF值。具体结果见表2。
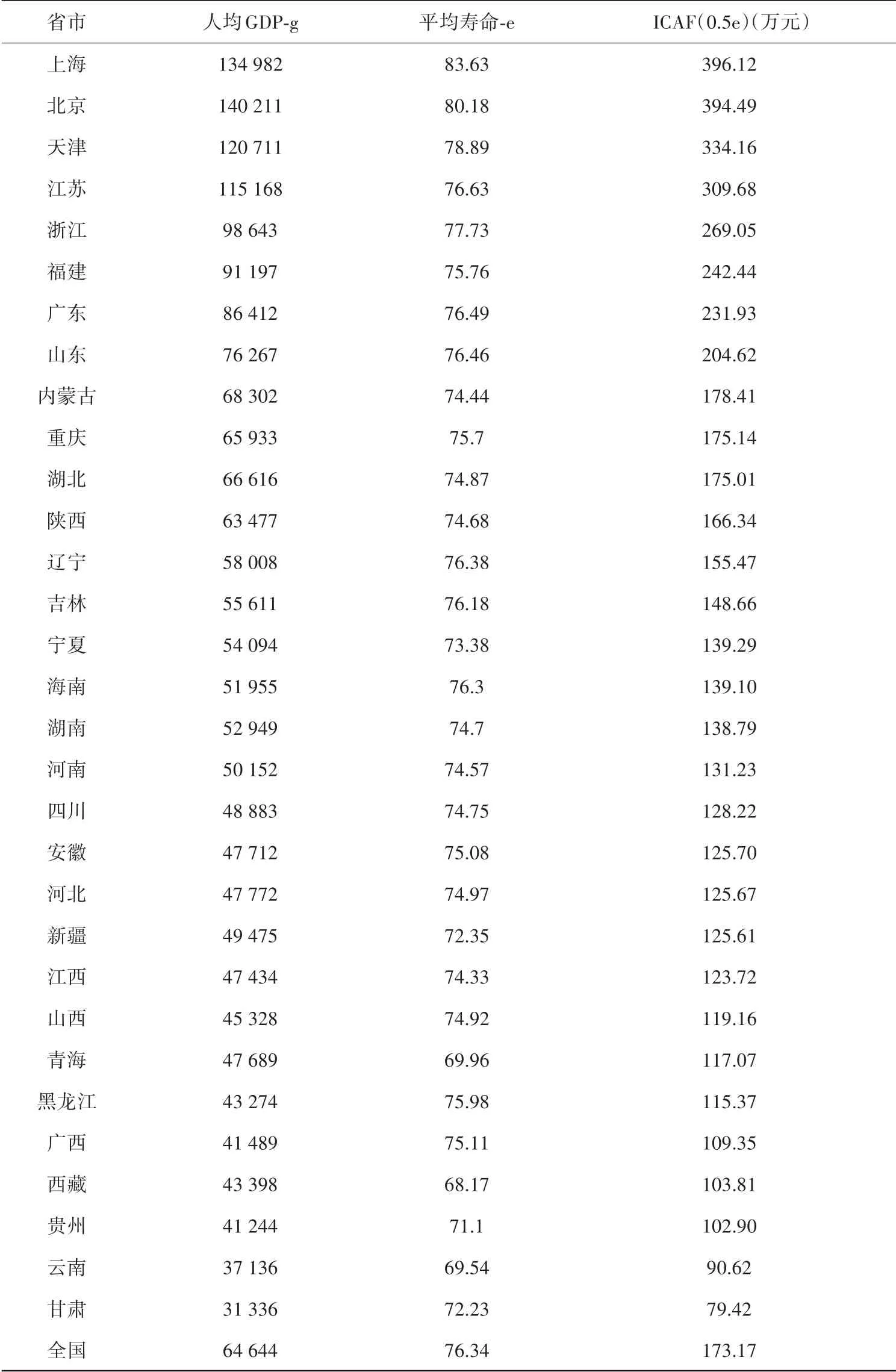
表2 2019年各省市ICAF值Table 2 ICAF value of provinces and cities
从表2可以看出,上海、北京2个直辖市的ICAF值接近400万,其挽救生命成本最高。全国的平均挽救生命成本约173万元,处于各省市的中等水平。
3 建筑运维阶段最优安全投资应用示例
3.1 最优安全投资方案验证
前文通过对改进的LQI公式进行推导,并赋予参数相应数值,得出了不同地区的避免死亡隐含费用ICAF值,其最终目的是计算降低风险的最优化投资,为决策者的投资决策提供依据。
由张舒等人[8]文献相关数据可知,2008-2012年我国煤矿的个人死亡率为1.564 5×10-3/年,若想将此值降低到英国的危险产业的最大可容忍风险标准1×10-4/年。基于前文的SLSC计算方法,调整相关参数,可计算得到在2013年社会需投入的最优安全资金为124.4亿元。同理按照2019年的数据进行计算,该数值约为187.34亿元。
查阅相关数据可知我国这几年在煤矿行业安全费用的实际投入约为170.5亿元/年。对比前文基于LQI的最优安全投入金额可知,我国煤炭行业的实际安全投入是较为合理的。多年的投入,也使得我国煤炭生产安全问题得到长足的改进,煤炭百万吨死亡率从2013年的0.3已下降至2019年的0.09,达到了中等发达国家的水准,个人死亡率已经降低为3.83×10-4/年,大幅度缩小了与发达国家的差距。该例子在一定程度上说明了基于LQI建立的最优安全投资方案的合理性。
3.2 应用示例
对于建筑运维阶段的安全风险,如果考虑增加投资以改善目前的风险状况,那么社会可接受的合理的投资金额同样可以通过基于LQI的SLSC值来确定。本例计算上海市2019应为降低建筑运维阶段中围护结构失效风险的合理投资金额。
由前文可知2019年上海市ICAF(0.5e)值为396.12万元,人口为2 423.78万。由上海建科工程咨询有限公司关于《城镇建筑结构运维安全风险识别及评估理论和方法》报告(后称《城建风险报告》)可知围护结构失效的死亡概率约为1.22×10-5/年。参考本文前面得到的建筑运维阶段个人可接受风险标准为10-6/年,可知该个人风险处于不可接受区域,如果现在要使得个人风险从目前的状态降低至可接受风险标准,则需要投入的资金为
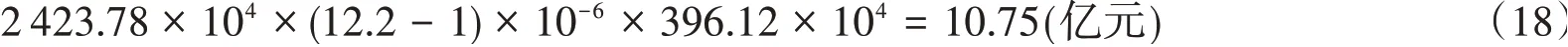
即为了将建筑运维阶段中因围护结构失效而死亡的概率降低到可接受的程度,则2019年上海市相关部门需投入到围护结构改善措施中的合理资金为10.75亿元。
由于缺少官方的精确数据,本文按以下方式估计2019年上海市在围护结构改善措施中实际投入。《上海市建筑业行业发展报告(2020年)》中指出2019年上海市完成各类旧房区改造面积约为1 343.3万m2;根据《住宅专项维修资金管理办法》,粗略估计维修改造费用约为150/m2;《城建风险报告》中相关资料显示围护结构发生事故概率在建筑运维阶段各种事故中占比为41.3%,则可以由此估算上海市2019年在旧区改造修缮工作中,针对围护结构的投入约为8.32亿元。对比前文模型计算值,可以认为上海市相关部门在该方向的资金投入较为合理。
4 结论
随着我国建筑业蓬勃发展,越来越多的建筑被投入使用并进入运维阶段,其中的安全事故的风险水平也在不断增加,因此在该领域进行风险评估与管理迫在眉睫,确立建筑运维阶段的风险评价标准是风险评估管理的前提。本文在目前各领域风险评价标准文献调研的基础上,基于我国国情制定了针对建筑运维阶段的风险评价标准,并基于改进LQI建立了建筑运维阶段的风险评价标准和最优安全投资方案,具体结论如下:
(1)给出我国建筑运维阶段风险可接受标准,其中包括生命、经济、环境及社会稳定风险4个方面,重点关注生命风险,并建议建筑运维阶段的个人生命可容忍风险标准为10-5/年,可接受风险标准为10-6/年。
(2)基于改进LQI给出了避免死亡隐含费用(ICAF)表达式以及社会挽救费用(SLSC)的计算公式。
(3)讨论了计算公式中3个关键参数即工作时间比例w、柯布—道格拉斯弹性系数β以及剩余生命Δe对ICAF值的影响,并给出了三者在建筑运维阶段的计算方法和建议取值。
(4)结合本文建议的参数取值给出了全国不同省市的ICAF值,对比了不同区域的生命拯救费用,发现上海、北京2个直辖市的挽救生命成本最高。
(5)基于建筑运维的风险分级标准和LQI理论,建立了建筑运维阶段的风险决策模型和最优安全投资方案,并计算了2019年上海市需在围护结构上的安全投入,结果为10.75亿元。并将此结果与基于现实数据估算的上海市2019年在围护结构上的维修投入进行对比,发现本文模型计算值与现阶段的投入接近,较好验证了基于改进LQI的风险评估方式是可行的。
