大前进比旋翼气动特性计算研究
2022-03-10邱逢昌樊枫
邱逢昌 樊枫
(中国直升机设计研究所直升机旋翼动力学重点实验室,江西景德镇 333001)
0.引言
随着作战需求的不断提升,常规直升机的速度和航程已难以满足现代战争的需求[1-2]。常规直升机由于受到前行侧激波和后行侧气流分离的影响,其速度受到很大的限制,为了获得较大的前飞速度,就需要降低旋翼转速[3],此时,旋翼在大前进比下工作。在工程上,常规直升机旋翼的计算,由于反流区较小,往往都是直接忽略其影响。而在大前进比下,反流区会扩散到整个后行侧,旋翼有一半时间都在后行侧转动,处于其中的旋翼不会产生升力或产生负升力,这种超常规的流动特性对旋翼气动载荷和旋翼配平都产生了直接的影响。
国外针对大前进比的气动特性开展了大量研究。早在上个世纪,国外先后进行了全尺寸的PCA-2旋翼[4],H-34旋翼[5]和UH-1D旋翼[6]风洞试验,试验表明升力系数和前进比呈负相关。由于这些试验缺少全面的气动载荷数据,难以对大前进比旋翼流动的机理进行进一步探索。为此,美国进行了全尺寸的UH-60A旋翼风洞试验,试验前进比达1.0。试验结果[7-9]表明:在同一总距下,前进比越大拉力系数越小;在前进比达到1时,推力不随拉力的增加而增大,出现推力反转现象;前进比越大,后行侧出现反流区,前行侧产生的升力远大于后行侧,也就需要更大的纵向周期变距实现配平。马里兰大学也进行了相关大前进比旋翼缩比风洞试验[10-14],其中,Berry B.[10]和Chopra I.[11]分别采用不同弦长和不同翼型旋翼进行风洞试验,试验结果表明推力反转出现在前进比μ=0.8~0.9,并且推力反转不受扭转和翼型差异的影响。Sugiura Masahiko[15]提出了一种新型的高速复合式直升机主旋翼桨叶外形,优化后的桨叶有效升阻比约为同等条件下UH-60A的两倍,同时能够保持与之相近的悬停性能。
国内目前针对大前进比旋翼气动特性研究较少,仅孔卫红[16]提出一种前进比达0.8的旋翼气动分析方法,主要是用桨叶动态扭转考虑动态失速对气动力的影响,加入动态失速对阻力系数的修正因子。仅通过理论计算与H-34旋翼试验进行对比,分析了大前进比状态下反流区对桨叶剖面迎角、升力以及阻力的影响。未得出旋翼气动性能、功率和载荷随前进比的变化规律。
本文运用CAMRAD II对HART II模型旋翼进行数值模拟,对大前进比下旋翼性能、功率和载荷随前进比和总距的变化开展计算研究,得到旋翼气动性能、功率和载荷随前进比的变化规律,为大前进比旋翼气动设计奠定相关理论基础,能够指导后续大前进比旋翼的研制。
1.计算方法及验证
CAMRAD II是一款知名的旋翼飞行器综合分析软件,在直升机多学科综合计算中应用广泛[17]。本文基于CAMRADII软件,以HART II模型旋翼[18]为模型,建立了一个大前进比旋翼计算模型。其中,气动模型采用自由尾迹模型,桨叶结构模型采用二维翼型+一维梁的中等变形梁理论,并取 6 阶模态桨叶模态,主要考虑三阶挥舞、二阶摆振、一阶扭转等主要模态。
首先,根据国外已有的HART II模型旋翼(旋翼参数如表1所示)实验数据[18],运用CAMRADII计算桨叶载荷并与试验值进行对比。HART II模型旋翼为BO-105直升机旋翼的40%缩比模型,试验状态为轴倾角5.3°的基准状态,额定转速1041r/min,悬停时桨尖马赫数 0.641,前飞速度33m/s,前进比0.15。图1给出了本文计算的HARTII模型旋翼典型的桨叶剖面载荷结果与试验值的对比。从图中可以看出,计算值与试验值吻合良好,表明计算模型合理有效。

表1 HART II旋翼模型参数

图1 HART II旋翼r/R=0.87桨叶剖面载荷计算值与试验值的对比
2.计算结果分析
大前进比状态下,由于受前行侧激波和后行侧气流分离的影响,需要降低旋翼转速。本文所有计算状态均是在30%额定转速状态下进行。
2.1 旋翼性能
图2给出了0°轴倾角状态下,不同前进比下旋翼拉力随总距的变化规律。从图中可以看出:在相同前进比下,旋翼拉力随总距的增加而增大;在相同总距下,旋翼拉力随前进比的增加而减小。
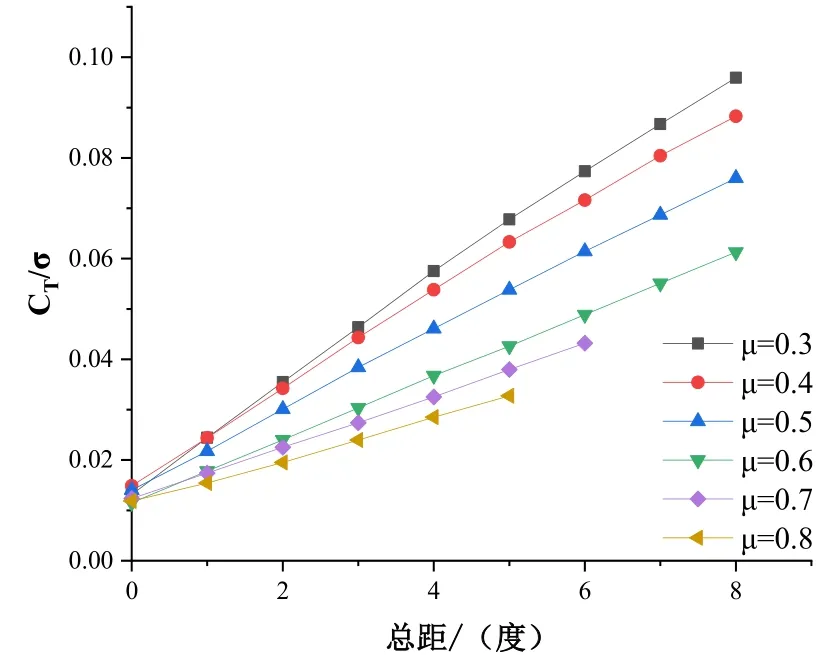
图2 不同前进比下旋翼CT/σ随总距的变化规律
为了平衡反扭矩,后行侧的攻角要增加以保持前行侧和后行侧的平衡,但效率会降低,特别是后行侧容易失速。因此,随着前进比的增大,拉力逐渐减小,这也是限制常规直升机飞行速度的主要因素。
图3给出了0°轴倾角状态下,不同前进比旋翼阻力系数随拉力的变化规律。从图中可以看出:在相同拉力下,阻力系数随前进比的增大而增大;在相同前进比下,前进比小于0.4时,阻力系数随拉力的增加而减小,前进比大于0.4时,阻力系数随拉力的增加而增大。
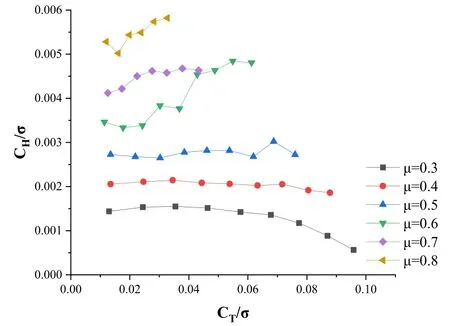
图3 不同前进比下旋翼CH/σ随拉力的变化规律
前进比大于0.4时,在相同拉力下,前进比越大,一方面反流区越严重,另一方面在大前进比保持相同的拉力需要更大的旋翼总距,此时处于失速的剖面越多,因此旋翼阻力越大。
图4给出了0°轴倾角状态下,不同前进比下升阻比随拉力的变化规律。从图中可以看出,0°轴倾角状态下,在相同拉力下,升阻比随前进比增大先增大后减小,在前进比等于0.4时,升阻比最大。
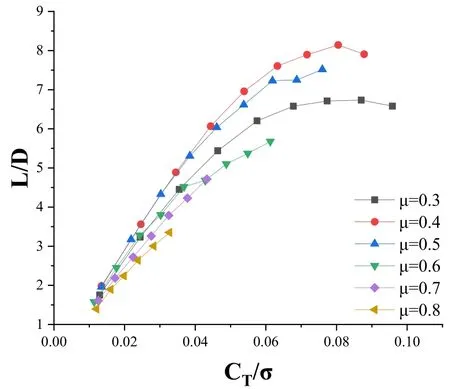
图4 不同前进比下旋翼L/D随拉力的变化规律
前进比大于0.4时,在相同拉力下,前进比越大,达到对应的拉力的需要更大的总距,在大总距状态下所对应的旋翼阻力就越大,因此升阻比相应减小。
2.2 旋翼功率
图5给出了0°轴倾角状态下,不同前进比下旋翼功率随拉力的变化规律。从图中可以看出,在前进比大于0.4时,相同前进比下,旋翼功率随拉力的增加而增大,且在大拉力状态下,旋翼功率迅速增加;相同拉力下,旋翼功率随前进比的增大而增大。

图5 不同前进比下旋翼功率随拉力的变化规律
图6给出了0°轴倾角状态下,不同前进比下旋翼型阻功率和诱导功率之和随拉力的变化规律。从图中可以看出:在相同前进比下,旋翼型阻功率和诱导功率之和随拉力的增加而增大;在相同拉力下,旋翼型阻功率和诱导功率之和随前进比的增大而增大,且在大拉力状态下,旋翼型阻功率和诱导功率之和迅速增加。
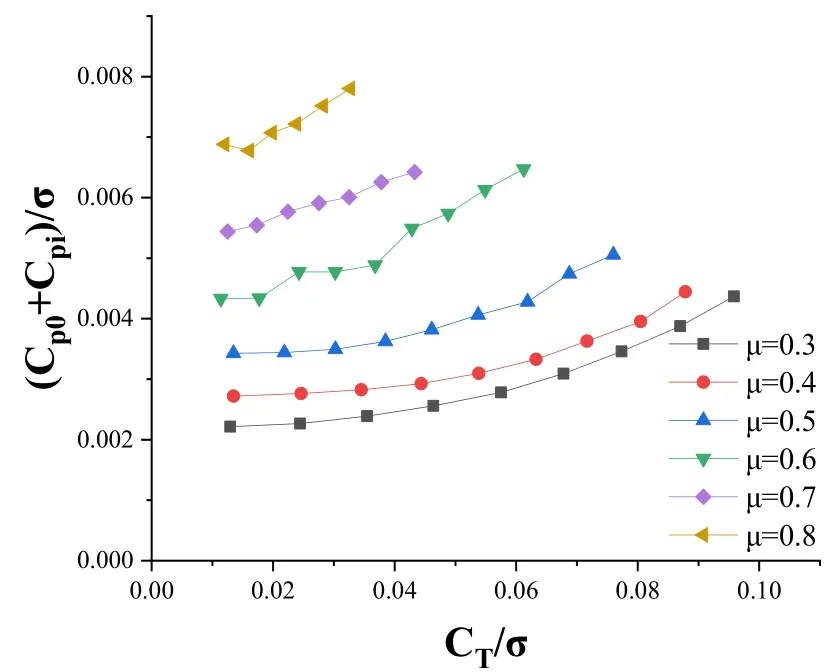
图6 不同前进比下旋翼诱导功率和型阻功率之和随拉力的变化规律
在相同前进比下,旋翼拉力增大,诱导功率也增大,与此同时桨叶剖面迎角增大使得失速的翼型剖面增加,从而导致型阻功率增大;在相同拉力下,旋翼型阻功率和诱导功率之和随前进比的增大而增大,这主要是因为阻力的增加导致了旋翼型阻功率增加。在后行侧,前进比越大反流区越严重,桨叶失速剖面越多,阻力也就相应的增大;在前行侧,前进比越大,前行侧桨叶压缩性越强,用于克服阻力的旋翼功率增加。此外,随着前进比的增大,旋翼型阻功率和诱导功率之和增加的越来越明显。
图7给出了0°轴倾角状态下,不同前进比下旋翼型阻功率随拉力的变化规律。从图中可以看出:在相同前进比下,旋翼型阻功率随拉力的增大而逐渐增大;在相同拉力下,旋翼型阻功率随前进比的增大而增大,且在大前进比状态下,旋翼型阻功率迅速增加。其中可以明显看出型阻功率占诱导功率和型阻功率之和的主要成分,在趋势上,型阻功率的变化规律决定了型阻功率和诱导功率之和的变化规律。
2.3 旋翼载荷
图8给出了,不同前进比下r/R=0.91截面处法向力系数在不同方位角的变化规律。从图中可以看出,在前行侧法向力最小,且随着前进比的增大负法向力也随之增大。后行侧由于受反流区的影响,前进比越大,反流区约严重,因此法向力在后行侧随着前进比的增大而减小。在大前进比时,在270°方位角时基本不产生升力。

图8 不同前进比下r/R=0.91截面法向力系数
3.结语
本文基于CAMRAD II对HART II模型旋翼在大前进状态下进行数值计算,得到旋翼性能、功率以及载荷在不同总距、不同前进比状态下的变化规律。通过对计算结果进行分析,得到以下结论:
(1)通过对计算典型的桨叶剖面载荷结果与试验值的对比,计算值与试验值吻合良好,表明计算模型合理有效。
(2)在相同前进比下,旋翼拉力随总距的增加而增大;在相同总距下,旋翼拉力随前进比的增加而减小。在相同拉力下,旋翼升阻比随前进比的增加先增大后减小。
(3)在相同前进比下,型阻功率与诱导阻力之和、型阻功率随拉力的增加而增大;在相同拉力下,型阻功率与诱导阻力之和、型阻功率随前进比的增加而增大。
(4)在r/R=0.91截面处,前行侧产生负升力,随着前进比的增大负升力越大,后行侧产生的升力随着前进比的增大产生的升力越小,且在大前进比时,在270°方位角基本不产生升力。
