模块化多电平型直流变压器的类两电平调制方法研究

史伟 殷新博 张锦涛

摘要：直流变压器作为未来高压直流电网互联的关键设备，将对远距离大规模新能源的消纳起到重要作用。现首先介绍了模块化多电平型直流变压器的拓扑结构和基本工作原理，然后提出了类两电平调制方法，并在此基础上分析了电容和电感的参数设计问题，最后通过仿真进行了验证。

关键词：模块化多电平;直流变压器;类两电平

中图分类号：TM41    文献标志码：A    文章编号：1671-0797（2022）04-0008-04

DOI：10.19514/j.cnki.cn32-1628/tm.2022.04.003

0    引言

可再生能源的大规模开发与利用、直流负荷的增多以及城市配电结构需求的多样性使得直流配电网成为当前研究的热点[1]。DC-DC变换器作为直流配电网中的关键元件，起到了不同直流电压等级間互联、负荷接入等作用。模块化多电平型DC-DC变换器因具有可扩展性强、功率等级高与输入/输出侧电气隔离等优点而适用于中压直流配电网[2]。

通过子模块工作模态的变化，理论上可以在交流侧调制出任意形状的电压波形，文献[3]中描述了一种最近电平逼近调制（Nearest Level Modulation，NLM）方法，即给定正弦调制信号，改变上下桥臂投入的子模块数量，使桥臂电压叠加后生成的交流输出电压为接近正弦的多电平形状，电平数量越多越接近于正弦调制信号。NLM调制算法相对简单，在高压直流输电等电平数量多的应用场景中，输出电压波形质量高;但在中压直流配电网的应用场景中，由于电平数相对较少，NLM调制应用较少[4]。

本文对模块化多电平型直流变压器的工作原理进行了详细介绍，包含功率特性与子模块电容、桥臂电感等无源器件尺寸的定量分析，并利用Matlab/Simulink搭建模型进行仿真研究，以验证理论分析的正确性。

1    类两电平调制方法及特性分析

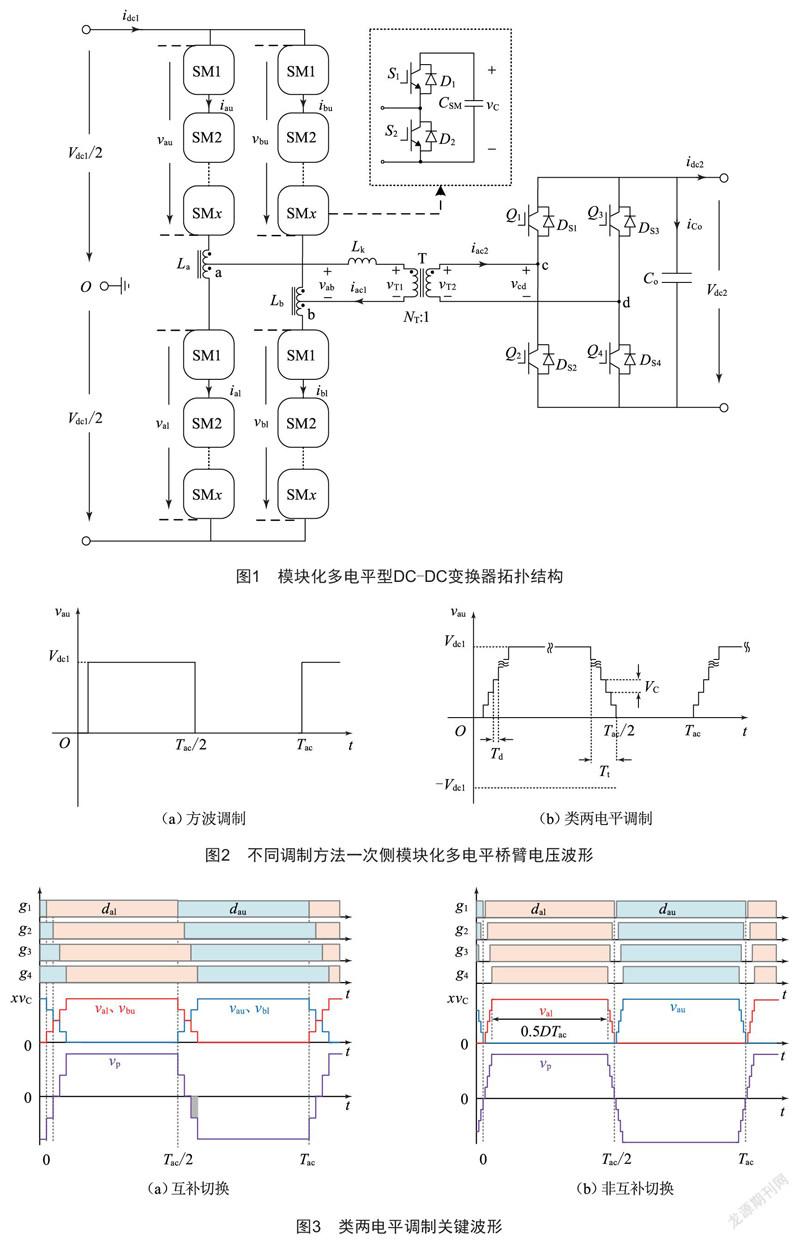
模块化多电平型DC-DC变换器拓扑如图1所示，由一次侧模块化的多电平、二次侧H桥、中频变压器T（变比NT：1）、一次侧直流输入电压Vdc1与二次侧直流输出电压Vdc2组成并实现能量在一、二次侧的流动。以一次侧a相桥臂为例，为了简化分析，假设桥臂每个子模块电容电压vC相等，且其平均值VC等于Vdc1/x，x为一个桥臂子模块数量;且忽略子模块电容电压纹波的影响。

由图2可以看出，方波调制下，桥臂电压vau在一个周期内波形为标准的两电平方波，在模块化多电平中体现为一个桥臂x个子模块同时投入电路中，即每个子模块开关S1同时导通，显然在电压等级高的应用场合会产生大的dv/dt。类两电平调制下，vau在每个时间间隔Td内投入或切除1个子模块，x个子模块投入或切除总共用时Tt=（x-1）×Td;通过这个过程，vau的电平变化由方波的突变变为类两电平中阶梯状的过渡过程，且阶跃值为子模块电容电压vC。合理设置时间间隔Td、直流侧电压Vdc1与子模块数量x，能获得可接受的dv/dt。

以每个桥臂子模块数量为4的情况为例，类两电平调制的具体实施过程如图3所示。

图3中，g1～g4分别为子模块开关器件S1的开关信号，无固定顺序，dal、dau为驱动信号占空比，桥臂电压过渡阶段时间为3个Td。图3（a）中模块化多电平工作在CS模式，驱动信号是一组时延为Td、占空比为0.5的方波，上下桥臂子模块工作在互补状态，上下桥臂投入的子模块数量之和恒为x，投入子模块电压之和等于直流侧电压;对角桥臂子模块工作在相同状态。图3（b）中模块化多电平工作在NCS模式，图中D为桥臂电压在交流周期Tac内值为Vdc1的持续时间与Tac/2的比值，通过改变g1～g4的脉冲宽度可获取不同的D。

类两电平调制一方面具有方波调制高直流电压利用率的优点，另一方面又克服了方波调制dv/dt过大的缺陷，因此该调制方法适用于模块化多电平型DC-DC变换器。

对于类两电平调制，若要分析子模块数量x与每个阶梯时间间隔Td对功率传输的影响，此时电压/电流变化的状态数过多，利用瞬时功率积分法将会增加计算的复杂度。本文利用相量法计算功率特性，该方法的核心是通过电压/电流量的傅里叶分解，在可接受的误差范围内取分解后的项数得到功率传输方程。下面将对相量法的计算过程进行详细分析。

模块化多电平对角桥臂子模块工作在相同状态，则一次侧等效交流电源vp表达式为：

令vp傅里叶级数为vp（t），由式（1）可得：

从而求得vp的傅里叶级数为：

从以上分析过程可以得出，在类两电平调制下，利用相量法进行分析时，过渡阶段对整体的影响很小，可视为方波处理。一次侧与二次侧移相角为β，则二次侧交流电源vs的傅里叶级数表达式与式（1）相同。

模块化多电平型DC-DC变换器具有类似于DAB的3种工作模式，第一种为降压（Buck）模式，即Vdc1>NTVdc2;第二种为升压（Boost）模式，即Vdc1

（1）整体分析：分析移相角对传输功率的影响;控制其余参数相同，取一次侧一个桥臂子模块数x为4;Td/Tac为1/200。

分析电感电压波形可以得到其等效纹波频率为两倍交流频率，即2fac，电感电压与电流的关系为：

式中：Lpdc为桥臂共模电流通路的等效电感，其值为2（Lp+Mp）。

则耦合电感单绕组电感量Lp为：

式中：k为耦合系数。

类两电平调制中忽略共模电流icm的存在，则NCS方式下桥臂电流组成中只需考虑交流侧电流。电容充放电特性表达式为：

式（6）中ε为电容纹波电压峰峰值ΔvC与平均值VC的比值，因此选取电容值的关键是计算电容充放电电荷ΔQ的值。电荷ΔQ与电容电流相关，根据上面的分析，只有在过渡阶段相应桥臂才有电流流过，即发生电容的充放电过程，首先确定了时间段;由于桥臂中每个子模块投入与切除的顺序不同，在计算電容值的时候应选取投入时间最长的子模块作为目标，因为该子模块电容充放电时间是最长的，电荷累积最多。实际上当移相角为π/2时就可实现有功功率最大传输，若限制移相角在0～π/2，电容值可进一步减小为：

（2）过渡时间占交流周期比例Tt/Tac很小，即为类两电平调制能够减小子模块电容值的原因。

2    类两电平调制仿真研究

为了对提出的调制方法进行验证，搭建参数如表1所示的仿真模型。

图4（a）为类两电平调制NCS工作模式下一次侧模块化多电平稳态运行时各桥臂电压/电流波形，桥臂电压过渡阶段阶梯数为3;图4（b）为桥臂电流波形;在过渡阶段桥臂电感被施加阶梯变化的电压，如图4（c）所示，该电压起到调节桥臂直流电流纹波的作用;在图4（d）中桥臂电流直流分量纹波频率为开关频率的2倍，其纹波峰峰值为7 A，直流侧电流idc1稳态值约为105 A，其纹波峰峰值为15 A，纹波系数r约为0.14，满足小于0.2的要求;仿真中采用脉冲循环法控制子模块电容电压的平衡，本处给出a相上桥臂电容电压仿真结果如图4（e）所示，可见平衡效果良好，对其进行区域放大，得到各个桥臂电容电压纹波峰峰值为28 V，纹波系数ε最大值仅为1.24%，满足小于5%的要求。

3    结语

本文主要对应用于模块化多电平型直流变压器的调制方法进行了研究，提出了类两电平调制方法，分析了功率特性和参数设计，最后在Matlab/Simulink中搭建模型对调制方法进行了仿真分析，验证了理论推导的正确性和类两电平调制方法应用的可行性。

[参考文献]

[1] 马钊，焦在滨，李蕊.直流配电网络架构与关键技术[J].电网技术，2017，41（10）：3348-3357.

[2] 胡子珩，马骏超，曾嘉思，等.柔性直流配电网在深圳电网的应用研究[J].南方电网技术，2014，8（6）：44-47.

[3] 熊雄，季宇，李蕊，等.直流配用电系统关键技术及应用示范综述[J].中国电机工程学报，2018，38（23）：6802-6813.

[4] 王丹，柳依然，梁翔，等.直流配电网电压等级序列研究[J].电力系统自动化，2015，39（9）：19-25.

收稿日期：2021-11-23

作者简介：史伟（1980—），男，江苏人，工程师，研究方向：直流输电技术。

3139500338254