多编组铰接式胶轮电车结构分析和试验

马 凯，徐洪德，陈秉智，刘 昱

(1.青岛中车四方轨道车辆有限公司，山东 青岛 266111；2.大连交通大学，辽宁 大连 116028；3.中车工业研究院有限公司，北京 100160)

传统有轨电车采用钢轮钢轨系统，由轮轨间振动引起较高的噪声，对城市生态环境影响较大。为克服噪声大的缺点，近年来世界各地的研发机构均进行胶轮电车的研发工作[1]。

城市轨道交通的胶轮电车系统目前主要有单轨系统、自动导向轨道系统和导轨式胶轮电车系统等模式。单轨系统和自动导向轨道系统均为一种车辆与专用轨道梁组合成一体运行的中运量轨道运输系统，存在建设周期长、建设成本高、转弯半径大等缺点。在城市公共交通系统中，传统的公共汽车存在着运量小、驾驶难度大、信息自动化程度低等缺点[2]。为了解决以上问题，加拿大庞巴迪公司于2000年研发出H型导向方式的胶轮电车(GLT)；法国NTL公司2006年研发出V型导向方式的Translohr胶轮电车。导轨式胶轮电车是一种采用橡胶车轮在常规路面上承载和驱动，由导向钢轮沿着道路中间导轨引导车辆运行的有轨电车[3]。

本文研究的多模块铰接式胶轮电车为三辆编组结构，采用胶轮走行部和单元式铰接车体结构，导向方式采用了防脱H型结构；采用DC 750 V车载储能装置供电；100%低地板设计，客室内实现无障碍贯通；通过的最小曲线半径为15 m，最大爬坡能力为13%，最高运行速度为80 km/h；可以与社会车辆混合路权行驶。

1 导轨式胶轮电车架构分析

导轨式胶轮电车采用悬浮车辆铰接编组架构。电车基本编组形式为“Mc1+ Tp+ Mc2”。其中，Mc为带司机室的动车；Tp为带受电弓的拖车[4]。端部车体底部布置动力走行部，中间车体与端部车体之间布置非动力走行部。图1为导轨式胶轮电车架构。表1为主要技术参数。

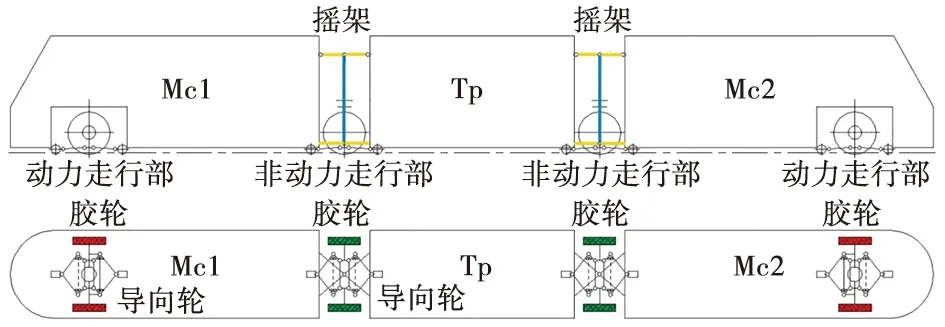
图1 导轨式胶轮电车架构图

表1 导轨式胶轮电车主要技术参数

车体为多模块通过铰接机构连接而成，摇架和铰接机构组成车体模块的铰接连接单元，同时也是车体与非动力转向架的连接单元。端部车体与中间车体通过铰接连接单元连接，形成一个铰接式编组。图2为车体编组结构原理图。

图2 车体编组结构原理图

走行部(图3)分为动力走行部和非动力走行部。动力走行部由门式轴桥(转向驱动桥)和导向机构组成；非动力走行部由门式承载桥和导向机构组成[4]。走行部与车体通过空气弹簧、垂向液压减振器等连接。采用双拉杆牵引方式。

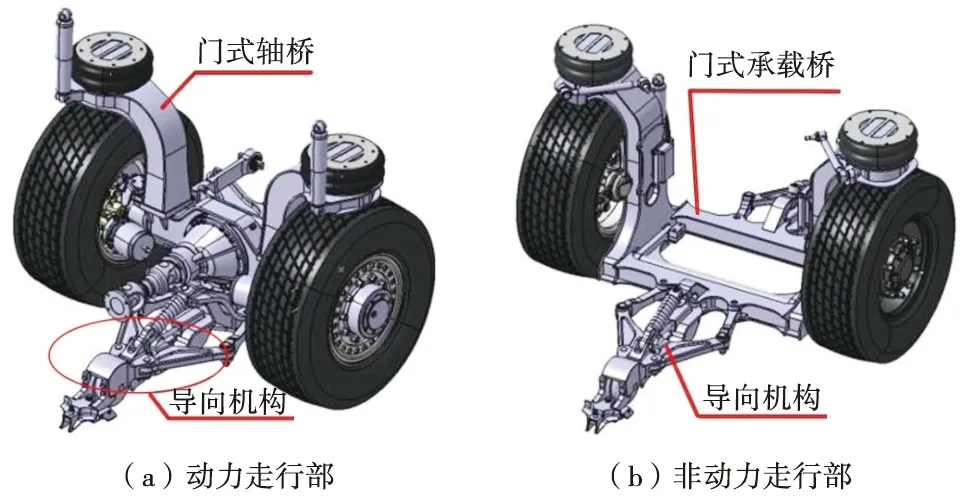
图3 走行部示意图

动力走行部的导向机构通过转轴与门式转向驱动轴桥连接(图4)，转向臂与轴桥的转向节连接，非动力走行部的导向机构直接与门式承载桥连接。

图4中可以看出，对于端部车，端部车体通过悬挂装置坐落在动力走行部；当导向机构的导向轮进入曲线导轨后，在导向轮与钢轨横向力作用下，使导向机构围绕转轴相对轴桥转动；在转向臂的作用下，橡胶车轮也发生转动，从而实现车辆的转向。对于中间车，摇架通过悬挂装置坐落在非动力走行部；当导向轮对着端部车进入轨道曲线后，在导向轮与钢轨横向力作用下，通过门式承载桥使橡胶车轮产生侧向力，从而实现车辆的转向。即该架构下的动力走行部为主动转向，非动力走行部为被动转向。

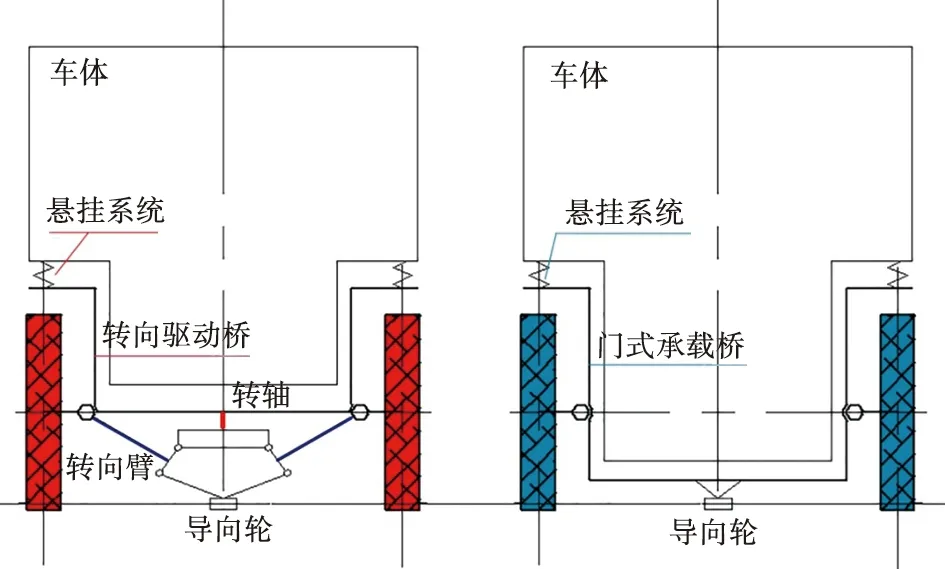
图4 走行部与车体关系简图

2 铰接机构的作用原理

由于电车主要在城市或郊区的公路上行驶，公路的路况相对钢轨比较复杂。当橡胶轮胎经过凸凹不平的坑道时，对于三辆编组的单元式铰接车体，前、中、后三节车体会先后出现侧滚，三节车体之间会形成较大的扭转角度，这就要求前、中、后三节车体之间在铰接点处关于纵向轴具有一定旋转自由度来缓解铰接处的受力。同时电车在运行过程中，会经过坡道，这就存在前、中、后三节车体有一节车体已经进入坡道，另外两节车体仍处于水平路面上等情况，这时两节车体之间形成一个夹角，这就要求前、中、后三节车体之间在铰接点处关于横向轴具有一定旋转自由度。因此，在车体与贯通道之间的连接轴承需要选用，以绕垂直轴旋转为主要旋转自由度，同时在纵向轴和横向轴也允许一定量的旋转自由度，这才能保证车辆顺利通过弯道、坑道、坡道等复杂线路情况。

图5为下部固定铰结构，采用了铰接轴承连接机构，两端与车体连接，为固定结构；中部安装在摇架上。保证固定铰座通过铰接轴承1绕垂直轴自由旋转，与中间摇架之间通过铰接轴承2绕垂直轴自由旋转，在水平和横向轴有一定的旋转自由度，满足了电车通过复杂线路的装配自由度要求。

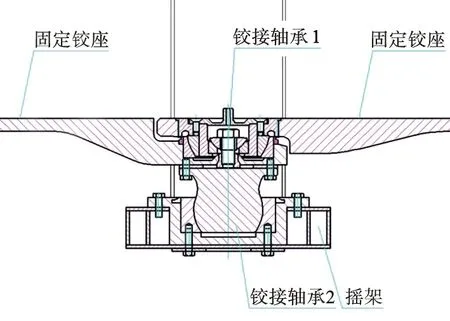
图5 下部固定铰结构

在车体端部与摇架之间安装抗侧滚装置来减小端部车体与贯通道之间的侧滚角度；由于中间车体两端连接的轴承都存在侧滚方向的自由度，因此安装三角拉杆式弹性抗侧滚装置来限制中间车体与摇架之间的侧滚自由度；而端车与摇架之间可以允许车体发生点头方向的运动，设置具有抗测滚装置的自由铰，如图6所示。弹性铰一端与车体连接；另一端通过关节轴承与摇架相连。车体在水平曲线运动时，弹性铰围绕摇架上的关节轴承1转动；车体在竖曲线运动时，弹性铰围绕车体端的关节轴承2转动。

图6 上部铰接结构

3 车体运动过程分析

当端部车体进入水平曲线而第一个非动力走行部未进入曲线时，端部车体上部与弹性铰围绕关节轴承1共同旋转；端部车体下部与固定铰围绕铰接轴承1共同旋转；实现车体转动，如图7(a)所示。

当端部车体与非动力走行部全部进入水平曲线时，摇架在走行部的作用力下将摇架转动，形成摇架与车体端部平行的姿态，如图7(b)所示。以此类推，车辆进入水平曲线；反之离开水平曲线。

当端部车体进入竖曲线时，固定铰座围绕铰接轴承2转动；弹性铰围绕着关节轴承2转动；自由铰的Z字型结构在外力作用下，发生垂向转动；从而端部车体相对中间车垂向转动，进入竖曲线。以此类推，编组进入竖曲线；反之，编组离开竖曲线，如图7(c)所示。

图7 车体曲线转动原理图

4 车体运动关系仿真

利用MSC ADAMS多体系统动力学软件，建立整车多单元运动学系统模型(图8)。点线运动副简化模型模拟导向轮与轨道的啮合关系；旋转运动副模拟纵向牵引杆连接关系；接触单元模拟橡胶轮胎与地面的摩擦滚动；弹簧单元模拟空气弹簧连接关系，球铰模拟弹性铰与自由铰的连接关系[5]。

图8 整车多单元运动学系统模型

计算时其端部车体下部的橡胶轮可以绕轮轴自转，还可以通过导向轮的作用实现转向；且假设橡胶轮的方向与其下部的导向轮方向一致。

4.1 小半径平曲线(R15 m)线路通过分析

为考察车体结构是否满足小半径平曲线通过，在MSC ADAMS中设计半径为15 m的1/4圆模拟该车拐直角弯，如图9(a)所示。检查曲线通过过程中主要部件之间的干涉情况及最大转动角。

图9 小半径平曲线通过模拟仿真计算

通过仿真计算可以得出，车体与走行部之间、车体与摇架之间均未发生干涉；通过图9(b)和图9(c)可以看出，车体与走行部之间的最大转角为16.7°，两车体之间最大转角为27.4°[5]，为车体尺寸优化提供依据。

4.2 R200 m竖曲线、13%坡道的通过分析

为考察车体结构是否满足小半径竖曲线通过，在MSC ADAMS中设计半径为200 m的竖曲线轨道。坡道的坡度为13%，根据相切原理，曲线长度为25.87 m，坡度为13%的坡道长取60 m，进行模拟计算，如图10(a)所示。检查排障器离地间隙和车体及摇架之间的转角。

图10 小半径竖曲线通过模拟仿真计算

通过仿真计算可以得出，车体与走行部之间未发生干涉；通过图10(b)和图10(c)可以看出，排障器最小离地间隙为10.4 mm，端部车体相对于前摇架的转角最大，为2.03°[5]；为关节轴承的选择以及车体尺寸的优化提供依据。

4.3 小半径S形曲线通过分析

为考察车体是否满足S形曲线通过，如图11所示，在MSC ADAMS中设计半径为15 m的S形曲线，轨道为两个1/2圆相切连接(注：计算时不设S形曲线的夹直线)。检查S形曲线通过过程中主要部件之间的干涉情况及相对的最大转角。

图11 小半径S形曲线通过模拟仿真计算模型

通过仿真计算可以得出，车体与走行部之间未发生干涉；车体与走行部的相对转角出现在前端部车体，最大转角为16.8°；两车体最大扭转出现在后端部车体与中间车体之间，最大为28.0°[5]。

4.4 固定铰受力分析

为了得到固定铰垂向和横向的受力状态，在MSC ADAMS中计算不同工况下的铰接装置受力状态。考虑约束方程和系统的动力学方程，ADAMS利用带拉格朗日乘子的拉格朗日第一类方程的能量形式求出约束反力的原理，采用NewMark逐步积分法，获得载荷时间历程，取最大载荷校核强度[6]。不同载荷状态下，固定铰铰接轴承安装孔处的最大垂向载荷为45 kN，最大横向载荷为55 kN。

5 曲线通过试验

车辆编组后，分别在15 m半径曲线、S形曲线和200 m半径竖曲线线路上进行试验(图12)。

图12 车辆曲线通过试验

试验结果表明，在15 m半径曲线线路通过时，车体与走行部无干涉；端部车体与橡胶车轮之间最小的间隙为100 mm。在S形曲线线路通过时，车体与走行部无干涉；端部车体与橡胶车轮之间的最小间隙为85 mm。在竖曲线线路通过时，车体与走行部无干涉；车体转动无异响。

在试验完成后，对固定铰、自由铰和弹性铰进行了拆解检查，铰接装置无损伤。