基于小波分解改进算法和峭度最大原则的滚动轴承故障诊断研究

孙 强，赵东波，王良涛，王孝卿，刘 洋

(中车大同电力机车有限公司，山西 大同 037000)

滚动轴承是旋转机械中最重要的且应用范围最广的零部件之一,据不完全统计显示，由滚动轴承损坏引起的故障数量大约占旋转机械设备故障总数的30%，在钢铁业，由于滚动轴承损坏导致的旋转机械设备故障率高达70%。因此，对滚动轴承的故障诊断方法进行研究具有十分重要的现实意义[1-2]。

通常情况下，在机车轴承相应的位置上安装智能传感器，在机车上搭载在线检测离线分析系统，对比检测轴承各个时域特征参数与正常轴承的各个时域特征参数，如若发现异常，系统自动报警，将数据发送给专业技术人员，由其对数据进行分析处理，从而确定滚动轴承是否出现故障，如若出现故障则确定故障的具体位置。针对后续的数据处理，本文提出了一种新的方法，由于小波分解改进算法能很好地克服小波分解传统算法过程中的频率混淆问题，而峭度的大小可以反映轴承的故障程度，因此采用小波分解改进算法和峭度最大原则对采集到的信号进行分析处理，提取故障特征频率，从而对滚动轴承进行故障诊断。

1 小波分解传统算法和小波分解改进算法

小波分解传统算法是将原始信号分别与高低通滤波器进行卷积，在卷积之后进行隔点采样，然后再让低频部分A1分别与高低通滤波器进行卷积，在卷积之后再进行隔点采样。依此类推，具体算法如图1所示。但是在卷积之后发现信号的长度会变长，即出现边界效应。在此基础上进行傅里叶变换时，是以长度增加了的信号为一个周期，就会出现主频的偏移。当边界效应越显著，主频偏移会越明显。为了克服主频偏移的问题，应该在信号与滤波器进行卷积之后将多余的信号长度去掉，这样可以保证信号的长度不变，即克服了边界效应，可以有效降低主频偏移的问题。

g.高通滤波器；h.低通滤波器；*.离散采样；A.近似系数；D.细节系数；↓2.隔点采样。

在小波分解过程中，由于小波滤波器的截止特性并不理想，低频部分会混有部分相邻的高频成分，而高频部分也会混有部分相邻的低频成分，这样就无法满足采样定理而出现频率折叠的现象。在小波重构过程中也会出现真实频率的映像[3-4]。针对上述出现的问题，后人提出了小波分解改进算法，可以有效地解决频率折叠现象和真实频率的映像问题，图2为具体算法。

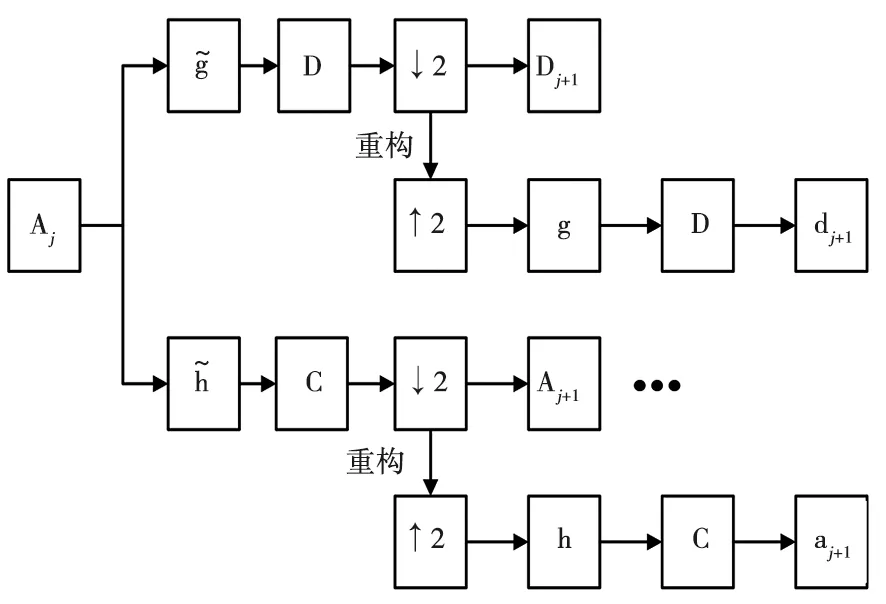
图2 改进小波算法

(1)

(2)

式中：x(n)——小波分解在第j层上的低频子带小波系数；

Nj——小波分解第j层分解信号的长度；

k——小波系数子带的个数，k=0，1，…，Nj-1。

上述小波分解改进算法是将原始信号分别与高低通滤波器进行卷积，卷积之后分别进行FFT、多余频谱置零及IFFT，然后再进行隔点采样，便可得到下一尺度的低频小波系数和高频小波系数。在重构过程中，先进行隔点插零，再与相应的滤波器进行卷积，然后再进行FFT、多余频谱置零及IFFT，就可保留信号的原有长度并消除多余频率成分，以解决频率折叠现象和真实频率的映像问题，依此类推，然后根据需求再对低频小波系数继续分解。

2 小波分解改进算法验证

以信号x(t)作为模拟故障信号，对传统小波分解算法和改进小波分解算法进行对比验证。考虑实际工况下振动信号含有噪声，因此对信号x(t)添加高斯白噪声n(t)，信噪比为-5 dB，同时选用db10正交滤波器，采样点数和采样频率分别设置为10 240和12 kHz，其中x(t)=sin(2π·500t)+ sin(2π·1 800t)+ sin(2π·4 000t)+n(t)，图3和图4分别为信号x(t)的波形图和FFT频谱图。

图3 x(t)的波形图

图4 x(t)的FFT频谱图

由x(t)的FFT频谱图可以发现，信号x(t)的故障频率为500.2 Hz、1 800 Hz和4 000 Hz，分别利用小波分解传统算法和小波分解改进算法对信号x(t)进行3层小波分解。

图5为小波分解传统算法频谱图，由图5可以看出，小波分解传统算法各频段存在频率混淆现象，同时出现1 200 Hz、2 000 Hz和4 200 Hz等虚假频率。

图5 小波分解传统算法频谱图

图6为小波分解改进算法频谱图。由图6可以看出，改进后的小波分解算法能够很好地克服传统小波分解过程中出现的问题，能够精准识别故障频率。小波分解传统算法和改进算法具体各频段频率范围和分解结果如表1和表2所示。

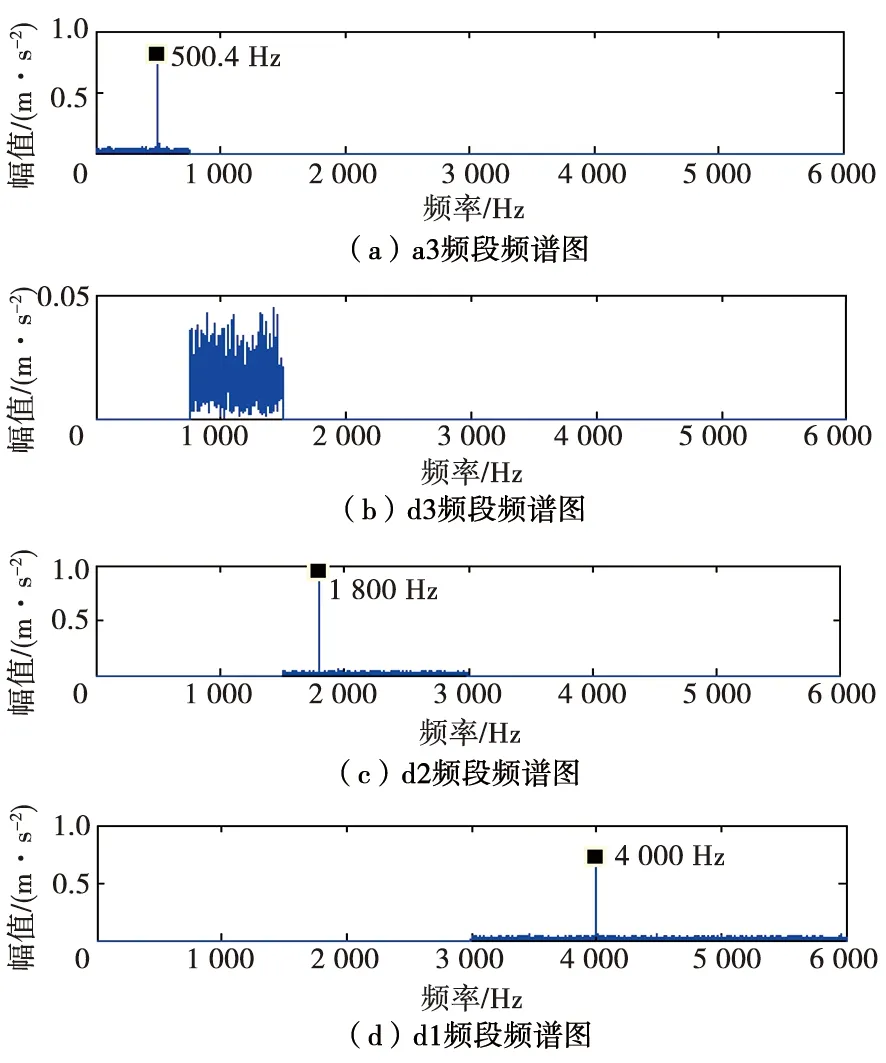
图6 小波分解改进算法频谱图

表1 小波分解传统算法和小波分解改进算法的各频段频率范围对比 Hz

表2 小波分解传统算法和小波分解改进算法分解结果对比 Hz

由表1和表2对比可以看出，小波分解改进算法的各频段频率范围和分解结果与理论结果相差不大，而小波分解传统算法则出现虚假频率和频率混淆。

3 实例研究

通过上述模拟信号验证了小波分解改进算法的可行性，下面将基于小波分解改进算法通过峭度最大原则来选取故障频段，然后再对故障频段进行Hilbert包络解调和傅里叶变换来查看故障频率，具体故障诊断流程如图7所示。

图7 故障诊断流程图

本文的试验数据借用美国凯斯西储大学提供的数据，通过故障频率的计算公式计算SKF 6205-2RS轴承故障频率[5-6]，具体数值如表3所示。

表3 SKF 6205-2RS轴承故障频率数值表 Hz

图8为正常情况和外圈故障下的时域波形对比图。

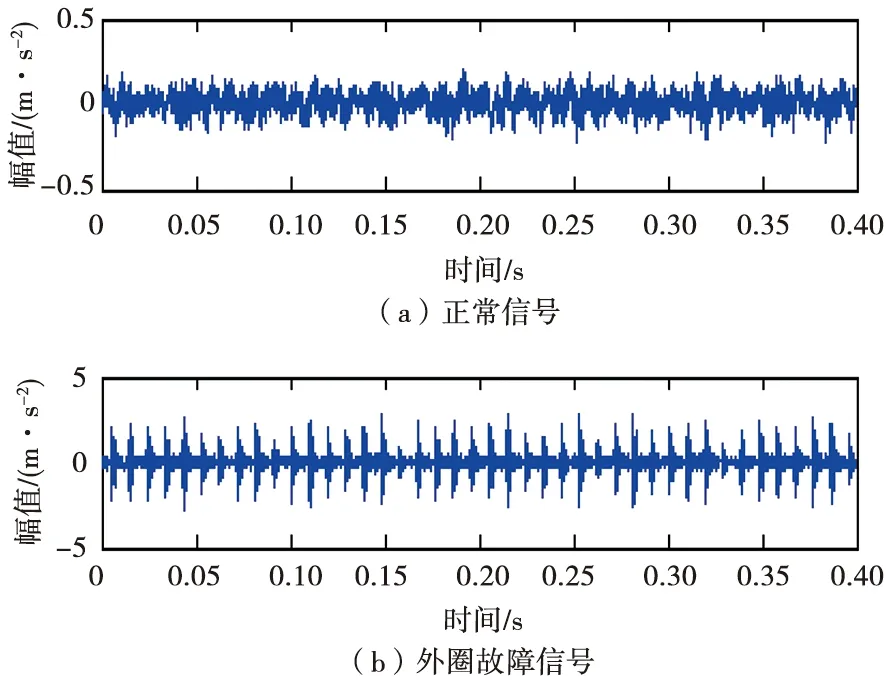
图8 正常情况和外圈故障下的时域波形对比图

通过对比可以发现，当滚动轴承的外圈出现故障时，其幅值跟正常时相比变化较大，而且出现周期性的冲击振动幅值，但是由于灰尘、异物等的存在也会引起振动冲击，因此需要通过进一步的诊断才可判定。

图9对外圈故障的采集信号进行了FFT频谱分析和功率谱分析。由图9可以看出，只进行FFT频谱分析或只进行功率谱分析均无法识别滚动轴承外圈的故障频率，故需要对该数据进行深层次分析。下面则采用改进小波分解算法进行进一步分析处理。

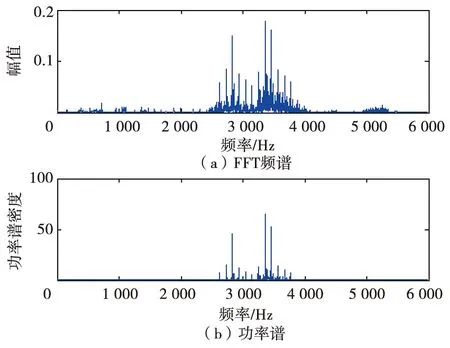
图9 FFT频谱分析和功率谱分析图

选用db10小波，利用小波分解改进算法对其进行3层分解，将其分为4个频段，分别为：a3频段、d3频段、d2频段和d1频段，上述4个频段的频率范围如表4所示。

表4 各频段的频率范围 Hz

对a3、d3、d2和d1上述 4个频段分别进行重构，各频段的重构信号如图10所示。由图10可以看出，在d1和d2频段的幅值较大，并且其波形跟外圈故障信号的波形相似，计算各频段的峭度值，具体数值如表5所示。

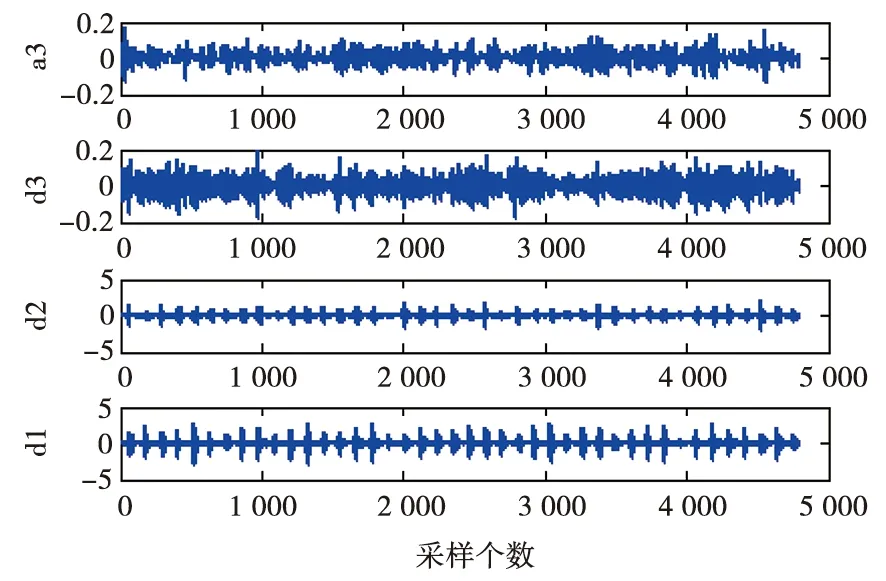
图10 各频段重构信号

表5 各频段峭度值

由于峭度指标对冲击信号比较敏感，故障特征信号一般积聚在峭度值较大的频段，而d1频段的峭度值最大。因此本文选取峭度值最大的d1频段进行重构，并对重构信号进行Hilbert包络解调，图11为其包络频谱图。

图11 小波分解改进算法后重构信号的包络频谱图

在图11中可以精准地识别出该滚动轴承的外圈故障频率为105 Hz，而上述理论计算的外圈故障频率值为104.4 Hz，因此可以确定是滚动轴承的外圈出现故障。

图12为基于小波分解传统算法，通过峭度最大原则选取故障频段，然后对故障频段进行Hilbert包络解调和傅里叶变换的重构信号的包络频谱图。

图12 小波分解传统算法后重构信号的包络频谱图

由图11、图12可知，小波分解传统算法和小波分解改进算法均能够对滚动轴承进行诊断，但是小波分解改进算法能够更加精准地识别故障频率，克服主频偏移的问题，有效地解决频率折叠现象和真实频率的映像问题。

4 结束语

本文通过对比分析小波分解传统算法和小波分解改进算法，并模拟故障信号对小波分解改进算法进行验证，然后在小波分解改进算法的基础上，利用峭度最大原则选取故障频段，最后对其进行Hilbert包络解调和傅里叶变换来查看故障频率。结果表明，小波分解改进算法具有很好的诊断效果，可以为后续机车轴承诊断提供方法支持，同时提高准确率。