基于变论域模糊-Smith的白酒勾调控制
2022-03-09周永帅
周永帅
庹先国1,2
韩 强1,2
刘 鑫1,2
(1. 四川轻化工大学自动化与信息工程学院,四川 宜宾 644000;2. 人工智能四川省重点实验室,四川 宜宾 644000)
与传统的人工勾调相比,白酒的自动化勾调具有产品质量稳定、生产效率高的优点,而勾调的精确性也成为系统设计的关键。1997年中船重工710研究所与稻花香集团研制了白酒勾调自动化控制系统,开启了酒企自动化改造升级的时代[1]。2005年衡水老白干集团成功利用计算机技术对传统的人工勾调操作进行了自动化升级,所开发的智能勾兑系统,在控制的精度、稳定性以及生产效率上均表现优良,且成品酒风味质量俱佳[2]。2010年贵州茅台酒业为了解决使用小容器进行白酒勾调产品质量不稳定,生产效率低下的问题,使用脉冲的气动调和、大容器的自动勾调等技术实现了白酒的规模化、智能化、优质化生产[3]。综上,白酒勾调智能化还处于刚刚发展的阶段,随着中国白酒市场不断扩大,以及走向国际化,白酒勾调对于实现品牌化、规模化起到越来越重的作用。
白酒自动化勾调系统在生产过程中,需要各种原酒及调味酒严格按照成品酒的配方比例,经过装配有输酒泵、流量计、电动调节阀等设备的管道输送至成品酒罐混合而成所需的成品酒,酒液的比例稍有不适便会影响成品酒的口感。目前酒液流量的精确控制存在以下难点:① 被控对象为累计流量属于过程控制量,由于管路输送距离等原因,对控制信号的响应具有时滞性[4];② 具有管路传输过程中管阻,水锤等非线性以及不确定因素的影响[5];③ 累计流量具备不可回调性,因此系统具有响应无超调的前提要求。
研究拟建立一种适用于白酒自动化勾调系统的流量精确控制算法,采用Smith预估补偿器消除时滞性对系统的影响,使用模糊控制解决系统数学模型建立不精确的问题,并且结合论域自适应方法提高模糊控制器的控制精度,以期实现白酒自动化勾调过程中酒液的精确传输。
1 白酒自动化勾调系统数学模型
由于白酒自动化勾调系统具有时滞性,非线性的特点,精确模型的建立非常困难,通过等效方法建立近似的数学模型[6]。白酒自动化勾调过程存在的环节:① 酒液开始在管道中传输至流经流量计之间,此时流量计尚未检测到数据,因此产生一个大滞后环节;② 流经电动调节阀瞬时流量的大小与阀门的开度相关,此时会产生一个一阶惯性环节;③ 由于系统存在大滞后环节,而其他环节的时间常数远远小于滞后时间,故其他的环节均可等效为比例环节;④ 由于系统的被控对象为累计流量,因此需要增加一个积分环节。以上各环节的乘积即为该控制系统的近似数学模型:
(1)
式中:
G(s)——控制系统的近似数学模型;
k——系统的总体增益;
T——惯性时间常数;
τ——纯滞后环节时间常数(与输送管道的距离以及液体的流速相关)。
系统的闭环框图如图1所示。

R(s). 被控对象累计流量的设定值 E(s). 累计流量与设定值的误差 D(s). 需要进行设计的控制器 U(s). 控制器的输出作用 Gp(s). 被控对象去除滞后环节的传递函数
2 控制算法设计
2.1 Smith预估补偿原理
在工业生产控制过程中,被控对象往往存在着滞后环节,滞后现象的存在会严重影响系统的稳定性。为了改善对系统的不良影响,国内外进行了大量的方法研究,其中最具代表性的是在1957年由Smith提出的预估控制器,即Smith预估器。其补偿原理为:由于滞后环节的存在,造成控制器对系统的调节作用即系统的响应曲线延迟了滞后时间τ,而Smith预估器却能使控制器提前滞后时间τ获知系统在当前控制作用下的响应,进而根据系统的偏差输出控制作用。从原理来看,经过补偿后滞后环节对系统的影响达到了被消除的效果,并且Smith预估器具有结构简单以及算法适用性强的优点,能够有效地解决系统时滞性的问题[7-10]。
由图2可知,其主要方法是设计一个补偿环节GB(s)与控制器D(s)进行反并联。
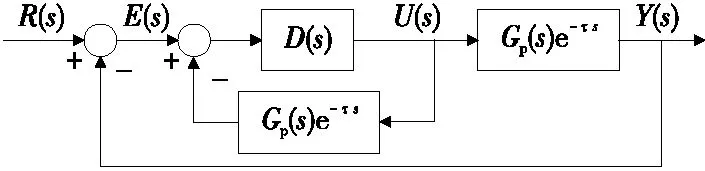
图2 Smith预估器补偿系统的闭环框图
补偿环节的传递函数:
GB(s)=Gp(s)(1-e-τs)。
(2)
Smith预估器补偿后的系统闭环传递函数为:
(3)
经过补偿后,系统的等效闭环框图如图3所示。

图3 补偿后系统的等效闭环框图
从图3可以看出,经过Smith预估补偿后,系统的滞后环节被排除在闭环回路之外,从而消除了滞后环节对系统稳定性的影响,而滞后环节只是将控制器的调节作用在时间上推迟了滞后时间τ,之后再对控制器D(s)进行单独设计即可。
2.2 PID-Smith控制算法设计
传统的PID控制算法设计相对简单,在工业生产控制中被广泛应用。在对被控对象的滞后环节进行Smith预估补偿后,对排除滞后环节的部分进行单独的PID控制器设计[11-12],研究拟采用的被控对象传递函数为:
(4)
其中:
(5)
由于系统控制要求无超调量,因此应将系统整定为典型的I型系统[13-14],故:
D(s)=kp。
(6)
由图3可知补偿后系统的开环传递函数为:
(7)
由于系统的阶跃响应无超调,因此系统应为临界阻尼二阶系统,即阻尼比取1,由式(7)可得:kp=0.001 25。
2.3 变论域模糊-Smith控制算法设计
2.3.1 模糊控制器的设计 模糊控制不依赖系统的精确数学模型,而是在现场操作者的经验以及专业人员的知识基础上构建起控制模型,然后根据相关的经验知识通过逻辑推理进行控制决策,最后完成对系统的调节作用,因此具有很强的容错能力[15-17]。
设计的两输入单输出模糊控制器:
(1) 输入语言变量E,表示设定流量Qd与实时累计流量Q的误差e=Qd-Q。
(2) 输入语言变量EC,表示误差e的变化速率ec=e2-e1。
(3) 输出语言变量U,表示控制器的输出量u。
(4) 模糊论域都设定为X=[-6,6],且都具有模糊语言值{正大(PB),正中(PM),正小(PS),零(ZE),负小(NS),负中(NM),负大(NB)},对于E表示实时累计流量相对设定流量:非常少、比较少、少一点、正好、多一点、比较多、非常多;对于EC表示实时累计流量变化速度:减速非常快、减速快、减速慢、不变、增速慢、增速快、增速非常快;对于U表示电动调节阀的开度变化量:阀门全开、增加量多、增加量少、不变、减小量少、减小量多、阀门全关。模糊语言值隶属度函数均选用高斯函数。
(5) 模糊规则语句的形式类如“if E is NB and EC is NB then U is NB”,其具体模糊规则如表1所示。
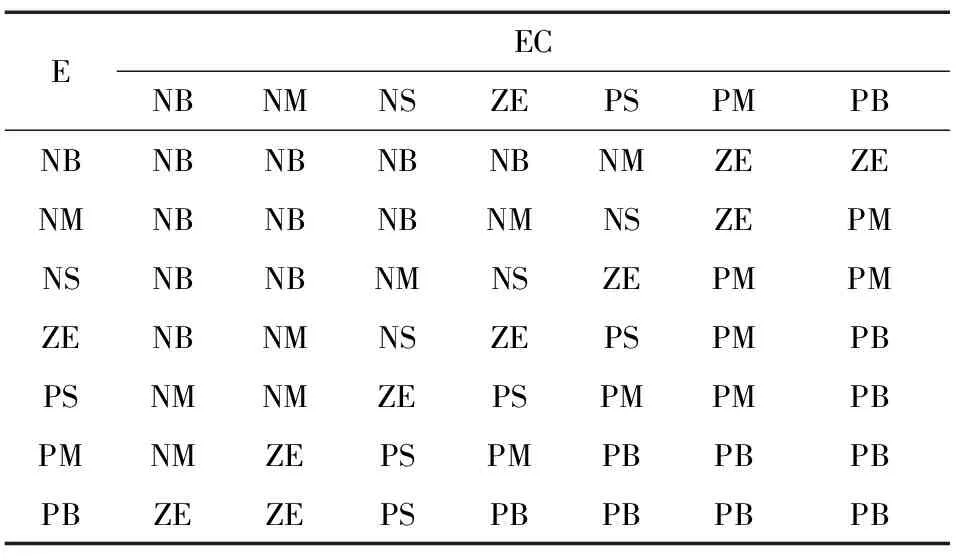
表1 模糊规则Table 1 Fuzzy rules
(6) 解模糊:模糊控制器的输出同样为模糊量,不能在系统中直接使用,而解模糊用于模糊量的精确化,清晰化。在解模糊的方法中,信息包含全面、计算精确的重心法使用频率最高。数学表达式:
(8)
2.3.2 变论域算法的设计 在模糊控制器的设计中,需要根据各个变量在系统中可能变化的范围来确定输入以及输出变量的实际论域,实际论域选择范围的不准确性会间接影响到量化因子以及比例因子取值的精度。在系统的控制过程中量化因子以及比例因子取值的不当会间接降低控制器对系统的控制精度,并且当系统趋于稳定状态时,输入变量的实际值只在实际论域的某一个很小的范围dδ内进行变化,如图4所示。
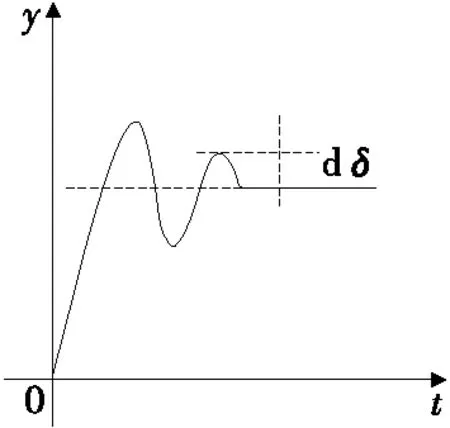
图4 变量的变化过程Figure 4 The process of changing variables
由图4可知,在系统趋于稳定状态时,由于误差以及误差变化率只在实际论域的某一很小范围dδ内变化,此时采用固定的量化因子只能将输入变量的实际值映射到模糊论域的很小区间内,不能遍布模糊论域的整个范围,此时进行模糊推理取得的控制量变化很小甚至保持不变,因此系统容易产生稳态误差,并且响应速度较慢。
为了解决此问题,李洪兴[18]提出了一种变论域的方法,即在系统趋向稳定的过程中,通过“论域伸缩因子”对变量的实际论域进行调节,当变量的实际值变大时论域变大,实际值变小时论域变小。量化因子以及比例因子的大小随着实际论域的变化而变化,实际论域伸张则因子变大,实际论域缩小则因子变小。在控制过程中,使用此方法能将变量的实际值模糊化后充分地分布在整个模糊论域,文中加以引用设计变论域模糊控制器[19-21]。
(1) 论域伸缩及论域伸缩因子:假设变量x初始的实际论域为[-xo,xo],在系统的控制过程中,具有可变实际论[-α(x)xo,α(x)xo],其中论域伸缩因子α(x)为关于变量x的连续函数,图5为论域的伸缩过程。
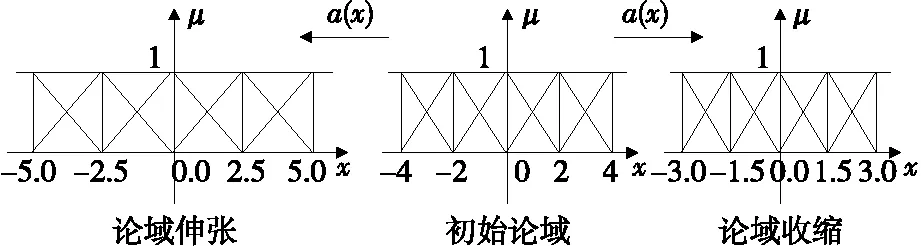
图5 论域伸缩过程Figure 5 On the process of domain scaling
且α(x)随x的变化一般具有如下规律:① 对于任意给定x的增量Δx,α的增量Δα,Δx与Δα呈正比;② 对于同样大的增量Δx,x越大,则Δα越大;③α不超过1,且α越接近1,Δα越小。
由此可知函数α(x)具有如下形式:
α(x)=1-exp(-kx2/2),
(9)
式中:
k——常系数。
k在一定程度上反映了控制算法的灵敏度大小,k的取值越大,α(x)趋近于1的速度越快,算法也就越灵敏,在x趋近于0时,α(x)的取值趋向于0。
(2) 论域伸缩因子的确定:取偏差e、偏差变化率ec和控制输出u的实际论域分别为[-Ee,Ee]、[-Eec,Eec]和[-Eu,Eu],其初始实际论域分别为[-Eeo,Eeo]、[-Eeco,Eeco]和[-Euo,Euo]。由式(9)取偏差e、偏差变化率ec的论域伸缩因子为:
(10)
αec(ec)=1-λexp[-k(ec/Eeco)2],
(11)
式中:
λ——最小论域取值范围系数(反映系统的控制精度)。
在控制过程中,控制输出u的论域伸缩因子αu同αe与αec的变化相关,取值公式:
(12)
(3) 变论域算法:取e、ec以及u的模糊论域的最大值均为Nmax,e*、ec*以及u*分别表示系统的实时测量误差,误差变化率以及经过比例调整后的实际控制量,其算法设计:
① 由式(10)~式(12)计算论域伸缩因子αe、αec以及αu;
② 调整e*、ec*以及u*的实际论域:
Ee=Eeo·αe,
我班开展了时光宝盒活动——让学生在纸上描绘出一个九年级的自己(包括成人、成才、成事三个方面),同时把纸条折叠成小船(从此岸到彼岸之意)、飞机(飞向梦想之意)或爱心(心想事成之意)等有良好寓意的形状,然后将所有学生的纸条共同保存在一个铁盒子里密封起来,在3年后的毕业典礼上打开。
(13)
Eec=Eeco·αec,
(14)
Eu=Euo·αu;
(15)
③ 调整量化因子qe,qec以及比例因子qu:
qe=Nmax/Ee,
(16)
qec=Nmax/Eec,
(17)
qu=Eu/Nmax;
(18)
④ 量化e*和ec*:
e=qe·e*,
(19)
ec=qec·ec*;
(20)
⑤ 对模糊控制器的控制输出u进行比例调整:
u*=qu·u,
(21)
式中:
u*——被控对象需要的控制量。
2.3.3 变论域模糊-Smith控制器结构 在对系统的滞后环节进行Smith预估补偿后,采用图6所示的变论域模糊控制器结构。
从图6可以看出:在控制过程中,通过论域伸缩因子对e、ec和u的实际论域进行了调整,量化因子以及比例因子随之而改变,使得系统的实时测量值e*以及ec*在模糊化之后能够分布到整个模糊论域,从而使模糊推理以及决策更为精准,在消除稳态误差的同时提高了控制器对系统的调节速度。并且此算法独立于模糊控制器之外,如此便可对相类似的系统设计相同的模糊控制器,只需对系统中变量的初始实际论域进行调整即可,简捷且直观。
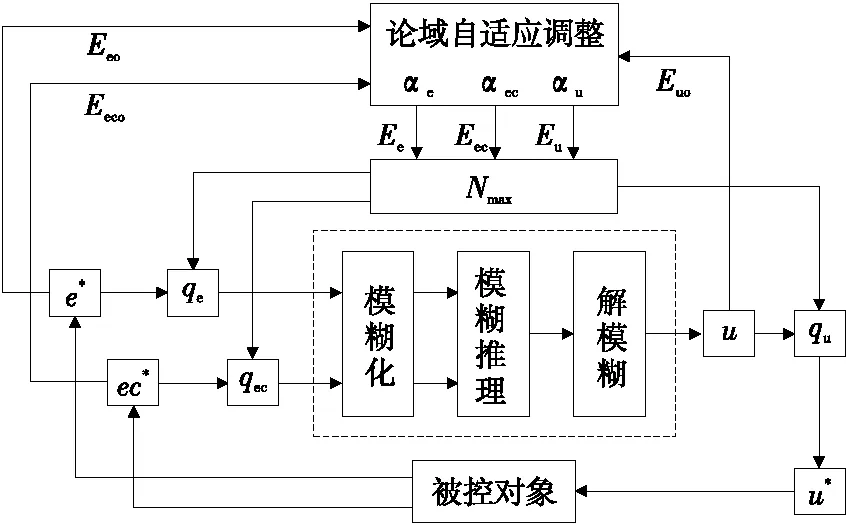
图6 变论域模糊控制器结构Figure 6 The structure of variable universefuzzy controller
3 仿真与分析
3.1 仿真参数设定
选用被控对象的传递函数为:
(22)
其中滞后时间τ=20 s,流量传输目标值为20。
3种控制器的设计:
(1) 对于PID-Smith控制器,控制器的kp=0.001 25。
(2) 对于常规模糊-Smith控制器,模糊控制器按照章节2.3.1进行设计,并且取量化因子qe=0.3,qec=7,比例因子qu=0.02。
(3) 对于变论域模糊-Smith控制器,模糊控制器同样按照章节2.3.1进行设计,并且结合章节2.3.2的变论域算法。取Eeo=20,Eeco=1.3,Euo=0.12,k=20,λ=0.99,Nmax=6,论域伸缩因子αe、αec按式(10)、式(11)进行计算,αu可由式(23)求得。
(23)
3.2 仿真结果对比分析
(1) 快速性:如图7所示,变论域模糊-Smith控制算法要优于常规的模糊-Smith控制算法和PID-Smith控制算法,对系统的调节时间最短,而PID-Smith控制算法的调节时间最长。

图7 响应曲线Figure 7 The response curve
为了分析其原因,将系统在PID-Smith控制、模糊-Smith控制及变论域模糊-Smith控制3种控制算法调节下的瞬时流量进行对比,如图8所示。在变论域模糊-Smith控制算法的调节下,系统的瞬时流量峰值最高且变化速度最快;在PID-Smith控制算法的调节下,系统的瞬时流量峰值最低且变化比较平缓;在常规的模糊-Smith控制算法的调节下,系统的瞬时流量以及变化速度均处于它们之间。因此,系统在变论域模糊-Smith控制算法的调节下达到稳态的速度最快。

图8 瞬时流量Figure 8 Instantaneous flow
(2) 超调量:为了分析系统在PID-Smith控制、模糊-Smith控制及变论域模糊-Smith控制3种控制算法的调节下是否出现超调量,将图7的响应曲线进行放大,如图9 所示。由图9可知,系统在变论域模糊-Smith控制算法以及PID-Smith控制算法的调节下无超调量,而在常规的模糊-Smith控制算法的调节下存在稳态误差而形成超调量,无法满足系统响应无超调的要求。
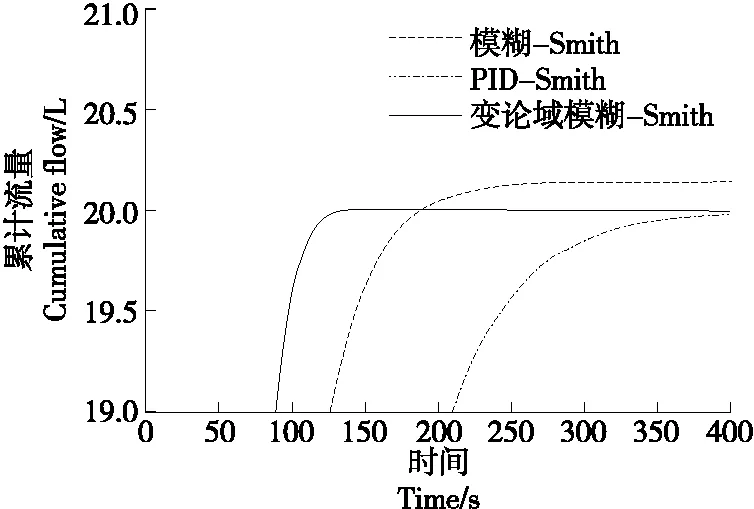
图9 放大后的响应曲线Figure 9 The enlarged response curve
为了分析其原因,将变论域算法对量化因子以及比例因子的修正效果展示如图10所示。由图10可知,随着误差e以及误差变化率ec的缩小,量化因子qec在变论域算法的作用下扩大到能使ec较好分布到整个模糊论域的数值,使得控制器进行模糊推理以及决策更加精准。而比例因子qu在算法的作用下随着误差趋于零而减小,使得控制输出量不至于过大而使得系统的响应变化过快,以致出现超调。因此,系统在变论域模糊-Smith算法的作用下控制精度更高,避免了稳态误差以及超调量的存在。
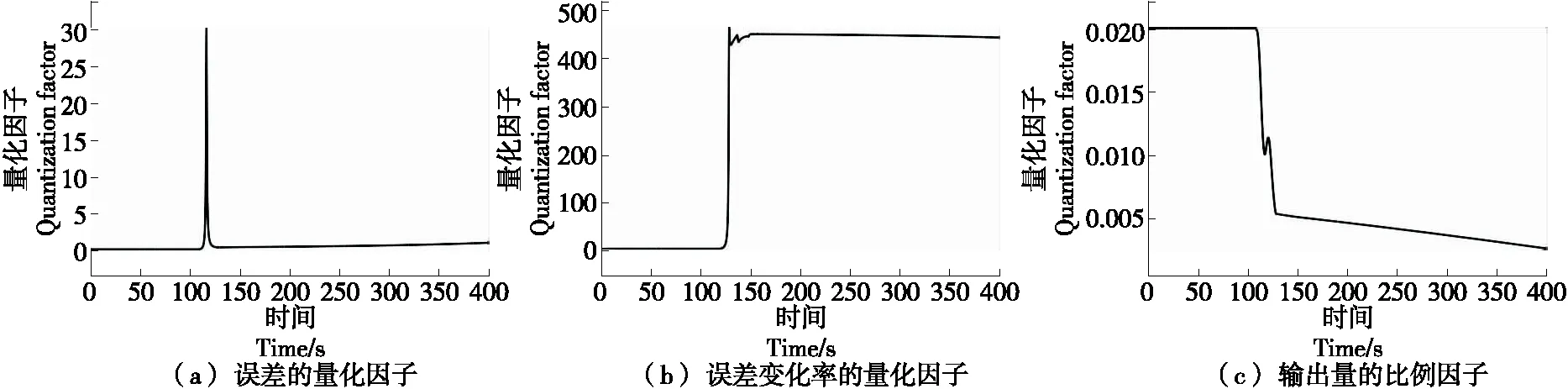
图10 量化因子以及比例因子的修正Figure 10 Modification of quantization factor and scale factor
(3) 鲁棒性:改变被控对象的传递函数为:
(24)
改变模型后系统的响应曲线如图11所示,系统在变论域模糊-Smith控制器的作用下响应无超调,而在PID-Smith控制器的作用下出现超调。因此,变论域模糊-Smith控制算法对数学模型的精确度依赖较低,鲁棒性更好。
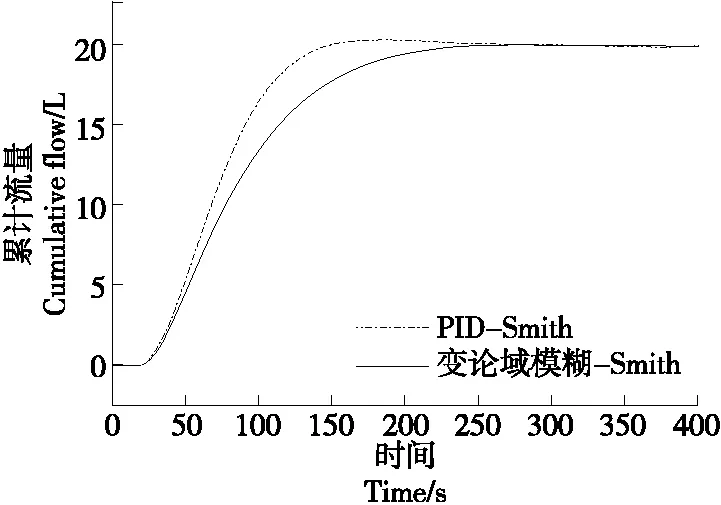
图11 改变数学模型后的响应曲线
(4) Smith预估器的补偿效果:如图12所示,在变论域模糊-Smith控制器移除Smith预估器后,系统响应曲线出现振荡,PID-Smith控制器移除Smith预估器后,出现超调量,均无法满足系统的控制需求,由此可见Smith预估器对时滞系统滞后环节的补偿作用。
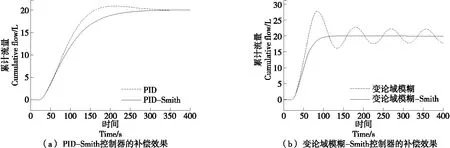
图12 Smith预估器的补偿效果Figure 12 The compensation effect of the Smith predictor
4 结论
为了实现白酒自动化勾调的流量精确传输,先建立白酒勾调控制系统的近似数学模型,再针对系统的特点,将模糊控制,Smith预估器以及变论域算法的优点进行了有效结合,最终设计出一种变论域模糊-Smith控制算法。通过Matlab对PID-Smith控制、模糊-Smith控制以及变论域模糊-Smith控制3种控制算法的调节作用进行了仿真验证,发现Smith预估器能够很好地消除滞后环节对系统的影响,并且与PID-Smith以及模糊-Smith控制算法相比较,变论域模糊-Smith控制算法的快速性以及鲁棒性更好,而且控制精度更高。由于Smith预估器依赖于系统精确的数学模型,尽管模糊控制器能在一定程度上降低系统数学模型不精确的影响,但不能完全替代Smith预估器的补偿作用。随着人工智能等高新技术的发展,具有自学习能力的人工神经网络在白酒勾调智能化控制中的应用有待进一步研究。
