基坑工程排桩内支撑围护结构局部破坏安全风险评价方法研究

2022-03-09李鹏飞朱良武张明聚谢治天万伟子

铁道勘察 2022年1期

关键词：轴力弯矩承载力

李鹏飞朱良武张明聚谢治天万伟子

(北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124)

随着城市现代化程度越来越高，基坑也在朝着开挖深度更深、开挖面积更大的方向发展。然而，部分深基坑工程发生了不同程度的事故，轻则引起邻近建筑物倾斜、开裂；重则导致基坑发生连续垮塌，邻近建筑物发生倒塌[1-2]，见图1、图2。

图1 新加坡某地铁基坑事故

图2 杭州地铁某基坑事故

目前，我国的基坑工程设计规范主要有基坑稳定性验算、支护结构强度计算和基坑变形计算三方面的内容[3]，对于基坑连续性倒塌方面却鲜有提及。在基坑连续破坏方面，程雪松等[4]通过显式有限差分法研究悬臂式排桩支护基坑局部破坏引发连续破坏的机理；郑刚等[5]通过模型试验研究内撑式排桩支护基坑局部结构破坏引发连续破坏机理；雷亚伟等[6]探究局部超挖对悬臂式排桩支护基坑安全性能的影响。宋利文[7]基于冗余度理论，提出一种提高环梁式基坑支护抵抗破坏风险的设计方法；袁小峰[8]研究内撑式排桩支护基坑局部结构失效的机理；顾家诚等[9]通过有限元法研究内撑式排桩支护基坑连续破坏机理；熊思嘉[10]从冗余度的角度，探索内撑式基坑在拆撑阶段的最不利工况，并提出优化方案。以上文献从不同的理论角度出发，研究了不同支护形式基坑连续破坏的问题，但在评价基坑连续破坏风险方面存在不足，未能有效地量化基坑破坏风险，并提出相应的风险控制方法。

通过MIDAS/GTX有限元软件建立内支撑式排桩支护基坑三维数值模型，采用拆除构件法模拟不同排桩的破坏，对剩余基坑支护结构进行连续性倒塌风险分析。同时基于结构承载力冗余度理论，针对该种支护形式基坑，提出局部结构破坏引起的风险量化指标和评价方法。

1 数值模拟

1.1 计算模型

某地铁车站明挖基坑采用“排桩+内支撑”的支护体系，地层以砂性土层为主，施工环境无地下水影响，基坑支护结构剖面见图3。

图3 标准段横断面(单位：m)

为减少边界效应对基坑数值模拟结果的影响，模型尺寸取84 m×40 m×36 m(长×宽×高)，基坑宽度和正常开挖深度均为12 m。基坑两侧沿Y方向设置40根排桩，桩间距1 m；沿基坑深度方向设置3排钢支撑，同列钢支撑垂直方向间距3.2 m，第一道支撑距离基坑顶部2.4 m；同排相邻钢支撑水平方向间距3 m，共设置13道支撑。在桩后0.5 m、地表至埋深12 m范围内，提高土体强度50 kPa，用来模拟桩体的挡土效果及桩间喷射的混凝土。

沿基坑Y方向通长布置围檩，基坑模型见图4。分别对前后边界面约束X方向位移，左右边界面约束Y方向位移，底面边界面约束X、Y、Z三个方向位移，最后对围檩沿基坑长度Y方向的位移和Z方向的转动进行约束。

图4 数值模型网格(根据对称性略去基坑一侧地层网格)

1.2 计算参数及工况设置

采用莫尔-库伦本构模型，摩擦角φ取30°，砂土黏聚力取0 kPa，泊松比取0.3。静止侧压力系数K0=1-sinφ，弹性模量E随土层深度线性增加，增长率为1.5 MPa/m[11]。计算过程中，不考虑地下水和止水帷幕的影响。

在模型中，支护桩和围檩均采用结构梁单元进行模拟。支护桩为φ0.8 m，长19.2 m的C30混凝土钻孔灌注桩。围檩断面规格为0.64 m×0.96 m(宽×高)。在实际工程中，钢支撑所承担的绝大部分荷载为轴力，为了研究方便，采用桁架线弹性单元模拟钢支撑，截面参数取0.630 m×0.012 m(直径×壁厚)，材料为Q235钢，EA为5.96×109N。通过MIDAS/GTS中的“印刻”连接桩与土的接触面，以模拟围护桩与土的界面效应[12]。支护桩依次编为1号～40号，钢支撑依次编为1号～13号，位置见图5。

1.3 数值模型验证

为验证数值模型的可靠性，建立与郑刚[5]现场试验条件相一致的单排内支撑式排桩支护基坑模型，得到正常开挖条件下23号支护桩的弯矩变化曲线，见图6。可以看出，排桩弯矩值随着开挖深度的增加而增大，当开挖至坑底时，最大弯矩为595.5 kN·m。而在开挖阶段测得的最大弯矩平均值为9.8 N·m，由模型相似比1∶16[11]计算出原型基坑在正常开挖阶段排桩最大弯矩理论值为642.25 kN·m，本模型计算值与理论值的偏差仅为7.28%，表明该数值模型具有较高的准确性。

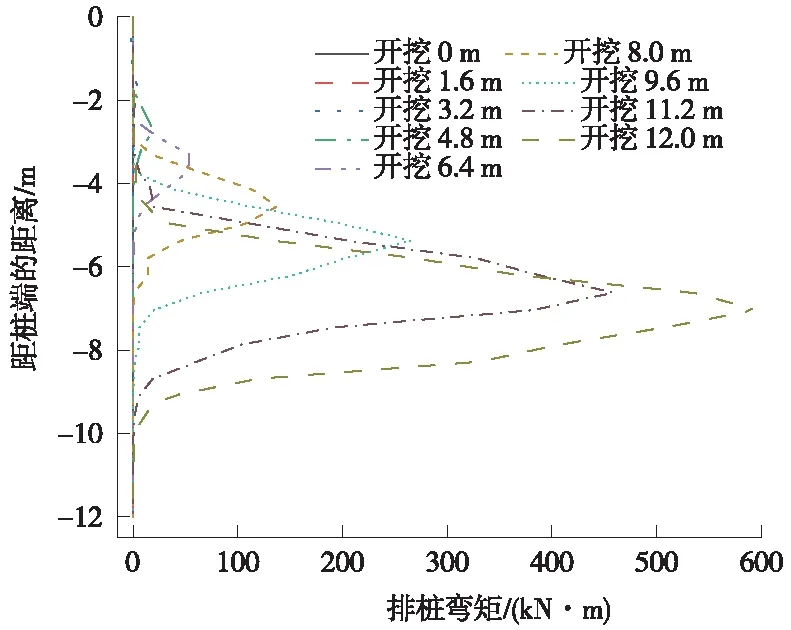
图6 排桩弯矩随开挖深度变化曲线

2 基坑局部结构破坏分析

基于拆除构件法原理的非线性分析方法，通过删除不同位置的排桩模拟局部结构失效，研究基坑剩余结构的力学机理。共设置6组工况：1根桩破坏(18号)，2根桩破坏(18号～19号)，3根桩破坏(18号～20号)，4根桩破坏(18号～21号)，5根桩破坏(18号～22号)，6根桩破坏(18号～23号)，以研究剩余排桩弯矩、钢支撑轴力变化规律。

2.1 排桩破坏对钢支撑轴力产生的影响

图7～图9分别为排桩破坏工况下不同排(B1，B2，B3)的5号～10号钢支撑轴力随排桩破坏数的变化曲线。

图7 第一排钢支撑轴力随排桩破坏数变化曲线

图8 第二排钢支撑轴力随排桩破坏数变化曲线

图9 第三排钢支撑轴力随排桩破坏数变化曲线

2.2 排桩破坏对邻近桩最大弯矩值的影响

图10为不同排桩破坏数下邻近桩最大弯矩值变化曲线，其中号7和8号钢支撑分别架设于21号桩和24号桩。从图10可以看出，当桩发生破坏后，邻近桩最大弯矩值均有不同程度的增大。当19号桩发生破坏后，20号桩最大弯矩值由174.6 kN·m增长到234.9 kN·m，增长34.5%。随着破坏桩的范围增大，排桩发生破坏的风险增加，进而会导致基坑产生连续破坏现象。

图10 邻近桩最大弯矩随排桩破坏数变化曲线

3 安全风险评价方法

3.1 结构承载力冗余度

结构承载力冗余度可以衡量结构物抵抗连续破坏的能力[13]。当结构发生局部破坏时，冗余的传力路径越多，剩余结构形成新的稳定状态的概率越大，从而能够有效避免连续破坏现象。

Frangopol等[14]认为，结构体系的冗余度受单个构件强度和整体结构承载力的影响，故提出基于承载力的结构冗余度Rl计算公式，即

(1)

式中，Li，Ld分别为结构发生局部失效前后的极限承载力。从式(1)中可以看出，当某个结构发生破坏时，该结构的极限承载力下降。当Ld接近0时，Rl=1，结构已失去大部分承载性能。Rl虽然可以反映某个局部破坏结构前后极限承载力的变化，但未能体现在局部结构破坏后基坑整体的风险程度。

3.2 安全风险等级划分

为更准确地量化内支撑式排桩支护形式基坑局部结构破坏而引起的连续破坏风险，定义反映基坑支护结构破坏风险的冗余度因子k。其包含排桩弯矩冗余因子kM和抗弯刚度冗余因子kD，以及钢支撑抗压强度冗余因子kN。kM、kD和kN分别指的是基坑局部结构破坏前后排桩最大弯矩、钢支撑轴力和排桩最大水平位移变化的百分比，有

(2)

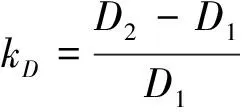
(3)

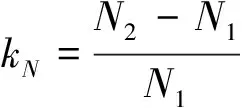
(4)

其中，M1、M2分别为基坑发生局部结构破坏前后排桩的最大弯矩值；D1、D2分别为基坑发生局部结构破坏前后排桩的水平位移值；N1、N2分别为基坑发生局部结构破坏前后钢支撑的轴力值。

从式(2)～式(4)可以看出，基坑局部结构破坏引起的剩余支护结构内力和变形越大，就越容易遭到连续破坏，基坑发生连续破坏的风险也越高。因此，为量化基坑发生连续破坏的风险，将k作为风险评价指标引入基坑连续破坏风险评价体系中。并进一步提出能够综合评价基坑支护抵抗连续破坏能力的抵抗破坏系数β，有

(5)

其中，[k]为达到支护极限承载力或极限位移下的极限冗余度值，k=n[k]为该二次函数对称轴，[k]≥k>0，n≥1。

基坑的初始破坏通常由支护体系局部内力或变形达到极限值引起，这意味着支护体系的内力或变形越接近其极限值，基坑发生破坏的风险越大，故通过[k]-k的值可以衡量基坑破坏风险，当k=[k]时该支护发生破坏。因此，抵抗破坏系数β由k=(kM，kD，kN)中各因子与极限冗余度值的最小差值确定，若[kM]-kM>[kN]-kN，则k=kN，[kN]-kN，有

(6)

当对称轴k=n[k]取不同值时，抵抗破坏系数β与冗余度因子k的变化关系见图11。

由图11可知，当支护体系所承受的传递荷载接近0时，也即冗余度因子k接近0，此时抵抗破坏系数β接近于1，基坑体系在抵抗破坏方面偏向于安全。

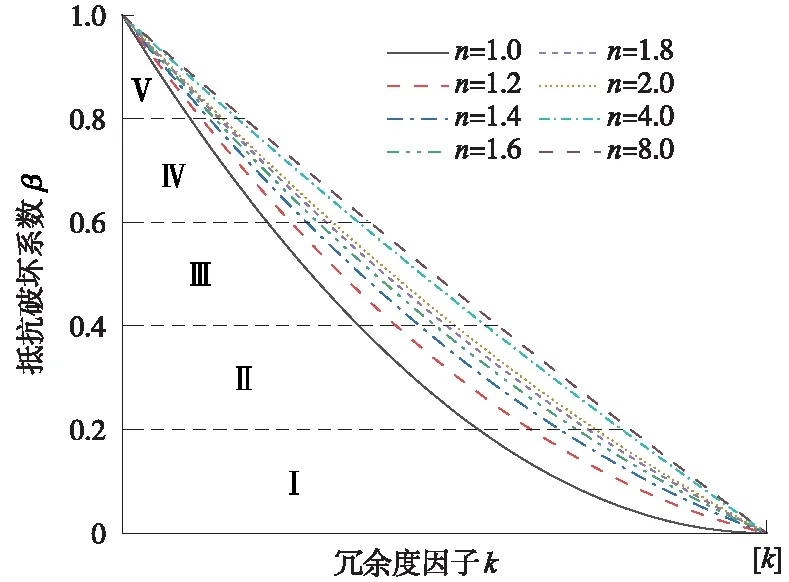
图11 β随k函数变化关系

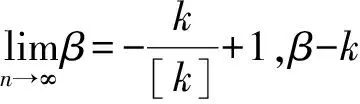
在进行综合风险评价之前，应对风险等级进行界定，以便更好地对基坑连续破坏风险进行量化处理。依据统计学的原理，认为评定每个基坑连续破坏风险的概率相等。因此，在界定风险等级时，结合抵抗破坏系数β的取值范围[0，1]，将基坑连续破坏风险划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ共5个等级[15]。从图11可以看出，当冗余度因子k一定时，n越大，β越大，基坑破坏风险等级越高。故将n=1的β函数曲线称为最保守估计曲线，n=∞时称为最乐观估计曲线。针对不同等级的风险采用不同的风险控制对策和处置措施见表1。