碳排放权交易的CO2减排效应研究——基于包含溢出效应的SCM

苏瑞娟 ，赵博娟，杨文青

（1.天津财经大学珠江学院 数据工程学院，天津 301811；2.天津财经大学 统计学院，天津 300222）

0 引言

碳排放权交易为一种基于市场机制运行的工具，通过经济激励对CO2排放进行总量控制，与基于行政处罚的排污准则相比，具有降低治污成本、促进技术革新，同时实现环境与经济红利的优势[1-4]。我国自2006 年成为世界上最大的CO2排放国家以来，排放量仍在逐年上升，2018 年的排放占世界的26%，同比增长1.9%[5]。为了实现减排目标，政府在2011 年宣布成立了7 个碳排放权交易试点，并于2013 年开始陆续实现交易。初始碳排放权的合理配置是碳交易市场有效运行的关键[6]，试点配额总量过于宽松及控排企业的初始配额过多会导致碳价格低迷甚至零交易，无法促进企业的减排行为[7]。刘传明等[8]则进一步对碳交易市场运行机制进行了数理模型分析，当低碳排放和高碳排放企业（即碳交易的供、需两方）均以利润最大化为目标而做出最优选择时，碳市场达到均衡并实现完全交易，而该均衡得以实现的前提仍是高碳排放企业初始配额不足且低碳排放企业配额富余。目前，各试点已形成了事前分配与事后调整动态结合的配发机制来实现更合理的分配[9]，张武林等[10]、赵立祥和王丽丽[11]、吕靖烨等[12]对各试点碳交易价格进行了研究，得到各市场已逐渐达到了不同程度弱式有效的结论。然而，碳排放权交易市场的目的不是交易，而是通过市场机制倒逼企业节能减排以及研发创新，最终实现环境红利[13]，因此各试点是否有效地发挥了减排效用及效用的持续性有必要进行实证检验。

我国多位学者基于省际面板数据，采用双重或三重差分模型（DID）实证检验了碳交易在省级层面具有积极的碳减排效应[14-18]；沈洪涛等[19]、刘晔和张训常[20]将同样的方法应用于微观企业得到了碳交易能够促进企业碳减排及研发创新的结论；周迪和刘奕淳[21]则应用匹配—双重差分模型（PSM-DID）对273 个地级市进行分析，得到碳交易对降低试点城市碳排放强度具有显著且持续的效用。然而广泛使用的DID 模型仅为所有试点估计一个综合或平均的效用，各试点市场制度设计的差异性及封闭运行使得试点的政策效果并不能一概而论，合成控制模型（SCM）为各试点碳减排效果异质性的探索提供了有力工具[8,22]。另一方面，学者对碳交易在经济、环境和社会方面的综合影响进行了广泛的模拟分析，例如Cui 等[23]、Lin &Jia[24]运用可计算一般均衡模型，得到碳交易市场能够促进节约减排成本、增加减排量，但交易市场不同运行模式下的作用大小有差别；Zhang 等[25]应用随机前沿技术、线性规划等综合方法得到碳交易能带来显著的波特效应，在GDP 不变的约束下使得碳排放强度下降19.79%～25.24%；Wang 等[26]应用基于DEA 的最优化模型得到基于市场的控排政策在节省减排成本及增加减排量方面均有显著的效用；张俊荣等[27]应用系统动力学方法得到碳交易机制能有效促进京津冀地区碳减排进程，但影响程度受机制设计例如碳配额总量、免费配额发放以及碳价的影响。

综上，大量实证以及模拟研究均表明碳排放权交易对CO2减排具有促进作用，但是以下两个问题在已有文献中均未考虑：（1）碳交易政策溢出效应的存在，可能会引起政策干预效应的低估或高估。（2）类似的碳减排政策，例如低碳试点城市、政府管控和税收等强制减排政策可能与碳排放权交易的作用发生混淆，从而导致政策效用的错误估计。鉴于此，本文采用Cao &Dowd[28]提出的包含溢出效应的合成控制模型（SCM-SP）对碳交易在每个试点的CO2减排效果分别进行定量研究，并进行了完备的检验，SCM-SP 在溢出效应以及混淆政策存在的情况下仍能对政策效用进行准确的估计，为全国统一碳排放权交易市场的创建提供经验支持。

1 模型和方法

1.1 合成控制模型

合成控制模型（SCM）由Abadie &Gardeazabal[29]提出，其基本思想是通过为实验单元合成相似的“反事实”对照单元来探索政策干预在宏观层面上所产生的效用。假定有N个地区T时期的观测数据，其中i=1 为实验单元，i=2,…,N为控制单元，t=1,2,…,T0为干预前的时期，t=T0+1,…,T(1 ≤T0＜T)为干预后的时期。用1 和0 分别表示受到和未受到政策干预，则i在时期t上的观测值。

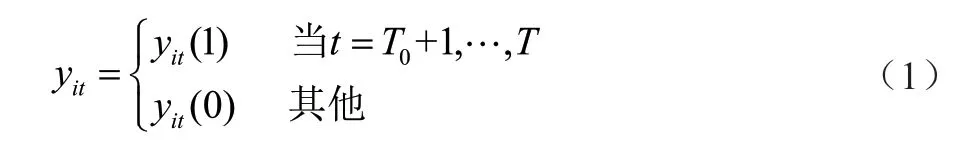
因此，地区1 受政策的干预效应为α1t=y1t(1)-y1t(0)，且在干预前y1t(1)=y1t(0)，然而在政策实施后，实验单元未进行政策干预的结果y1t(0)是不可观测的，需通过利用干预前的信息为控制单元选择最优权重对实验单元进行合成，并基于合成的估计值估计政策的效果

Ferman &Pinto[30]研究了传统SCM 估计方法[31]在政策干预前时期合成不完美时的统计性质及缺陷，并提出在合成值中加入截距项对实验单元进行合成，即：

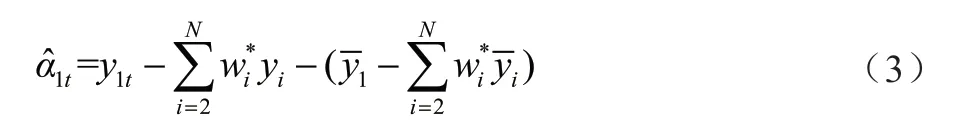
去均值估计量与Doudchenko &Imbens[32]对传统SCM 扩展得到相同的结果。

1.2 溢出效应的合成控制模型（SCM-SP）

上述的SCM 均不允许政策溢出效应及混淆政策的存在，即假定“非实验单元不受干预效应影响”。而碳排放权交易对CO2减排存在不可避免的溢出效应，原因为：（1）由“避难者天堂”假说及区域温室气体（RGGI）的经验，企业因寻求更有利的政策而进行区域间转移，进而引发试点与非试点之间的碳泄漏[33]。（2）非试点地区企业可能受到附近试点政策的“文化熏陶”，并依此对自身的行为进行调整。（3）碳交易首先促进试点地区企业进行技术创新，而技术的快速传播使得非试点区域间接受到影响。Abadie 等[34]在研究德国合并对西德经济的影响中曾提出溢出效应可能会使传统的SCM 对政策的干预效应做出偏误的估计，但并未给出具体的解决方法，Cao &Dowd[28]基于Ferman &Pinto[30]首次提出了包含溢出效应时合成控制模型（SCM-SP）稳健的估计量及统计推断过程，并证明了其在溢出效应存在情况下的优良表现。

1.2.1 估计

假定有p个控制单元受政策溢出效应的影响，则溢出结构矩阵可由以下N×P的矩阵A来表示，即：

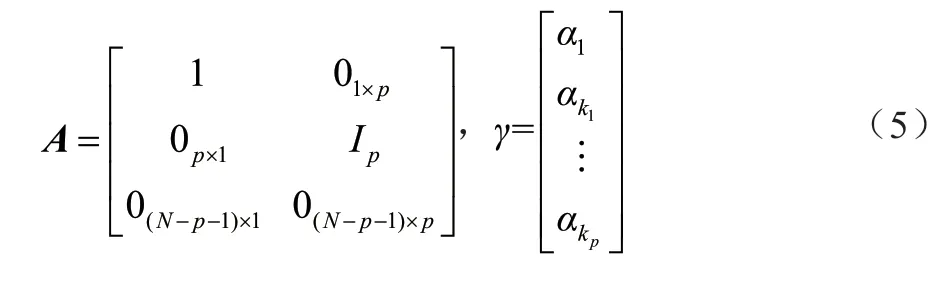
类似于空间计量经济学中的空间权重矩阵，A取值为1 的元素表示受政策影响的单元（包括直接政策效应的和间接的溢出效应）的位置，并且看作是已知的。由于溢出效应可以看作一种特殊的干预效应，因此在A中并不需要将两者进行特别的区分。本文仅考虑线性的情况，假设干预及溢出效应向量α可以看作某些未知参数γ的线性变换，则：

从而将α的估计问题转化为对未知参数γ的估计。

将式（2）扩展到对每个单元进行合成，则有：

1.2.2 统计推断

Cao &Dowd[28]将P 检验[35]推广到SCM-SP 中，由干预前残差估计值构建统计量来进行干预效应及溢出效应的统计推断以及区间估计，本文仅对置信区间的构建进行介绍。

将τ设定为0.025，从而得到干预效应95%的置信区间。

2 CO2排放量测算及其变化趋势

2.1 CO2排放量测算

由于碳排放权交易仅在试点内部进行，因此以省域边界测量各省份CO2排放量以保持与政策的一致性。能源消耗和水泥生产是CO2的两个主要来源，本文对二者的CO2排放量进行测算[16]，即：

地区能源平衡表中列出了详细的各种能源“终端消费量”数据，其中“用作原料、材料”的终端消费不是燃烧用途而不产生CO2；电力、热力在生产阶段而非终端消费阶段产生CO2，因此用于火力发电和供热所消耗能源产生的CO2需进行考虑。因此，地区i在t时期能源用途消耗的第j种能源的总量=（终端消费量-用作原料、材料）+火力发电和供热的“加工转换投入量”（“其他能源”指核能、风能、水能等清洁能源，其产生的CO2可以忽略不计，因此不再考虑）。地区i能源消耗产生的CO2排放量（万吨）为：

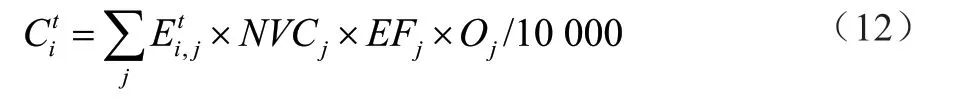
式中：NVCj、EFj、Oj分别为能源j的净热值、CO2排放因子及碳氧化率，17 种能源的上述信息采用Liu 等[36]中的取值，如表1 所示。

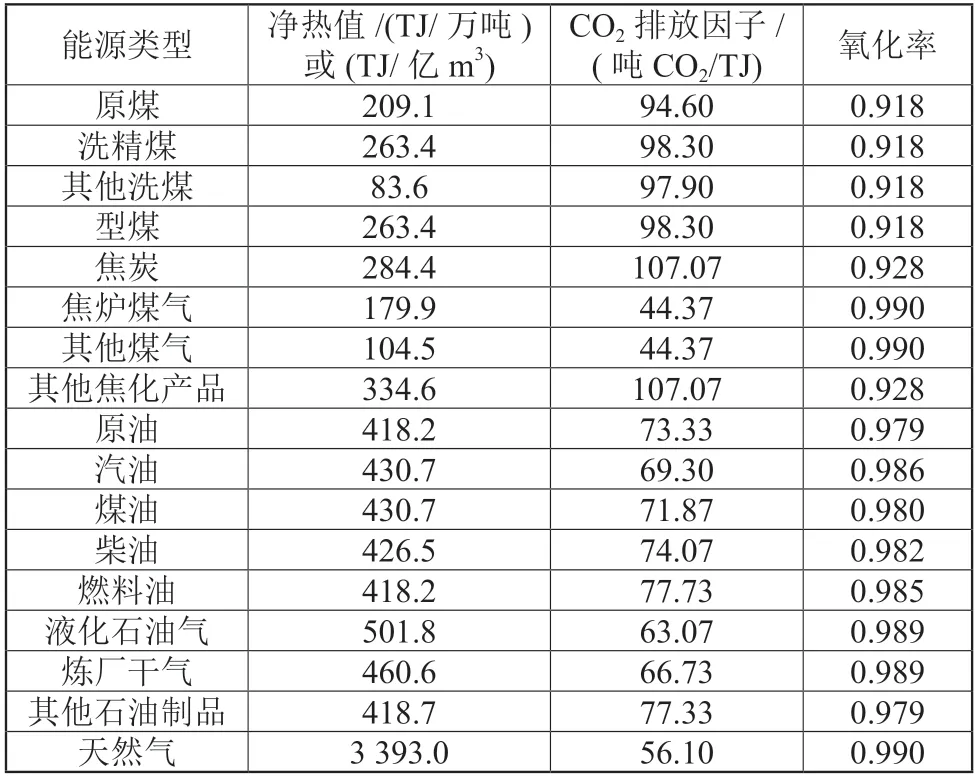
表1 各类能源的CO2排放因子及氧化率

水泥生产产生的CO2排放量为：

式中：为地区i的水泥生产量；EFcement为水泥的CO2排放系数，其取值为0.5272 万吨CO2/万吨水泥[16]。

地区能源平衡表来源于1996—2017 年《中国能源统计年鉴》，其中2010 年及之后的能源平衡表列出了较表1 更加详细的石脑油、润滑油等油品种类以及液化天然气的数据，本文将其分别与相关项“其他石油制品”以及“天然气”进行合并，以保持与2010 年之前口径一致。水泥产量来源于国泰君安数据库。由于港澳台及西藏地区能源平衡表缺失，本文仅考虑30 个地区，其中重庆仅包含1997—2016 年共20 年的数据，其他29 个地区均包含1995—2016 年共22 年的数据。

2.2 CO2排放量的变化趋势

由式（11）测算出各地区在观测期内的CO2排放总量，本文按照是否实施了碳排放权交易政策将所有地区分为两组，其中北京、天津、上海、湖北、广东和重庆6 个试点地区归为实验组（由于深圳属于广东，不再分开考虑），剩余的24 个非试点地区为控制组，试点以及非试点在观测期内各自的年均排放总量及随时间的变化趋势如图1 所示。非试点的CO2排放量从2002 年开始超过试点，随着两组都经历了至2011 年之间的快速增长时期，两组地区的排放差距呈现扩大的趋势；从2012年开始，两组地区排放量增长速度明显下降，并且实验组于2013 年呈现下降的趋势，两组的差异进一步扩大。

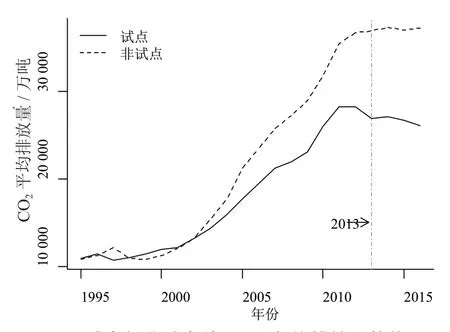
图1 试点与非试点地区CO2年均排放量趋势

3 结果分析及稳健性检验

3.1 结果分析

由于各试点碳交易市场存在异质性，因此分别对实验组的每个地区用其他24 个地区进行加权合成，估计碳排放权交易在不同省份的减排效果。设定每个试点的溢出矩阵A1为一阶邻接权重矩阵，即将具有相同边界的地区看作受政策溢出效应的影响。因此，北京、天津的溢出效应省份均为河北；上海的为江苏和浙江；湖北的为安徽、江西、河南、湖南和山西；广东的为福建、江西、湖南和广西；重庆的为湖南、四川、贵州和陕西。

本文选择试点的交易年——2013 年作为政策的干预时点。表2 为各试点的最优权重估计以及干预前平均的相对估计误差（RMSPE）①相对的绝对值误差计算公式：，图2 分别为每个试点CO2排放总量的观测值及相应的反事实合成试点的估计值及其95%的置信区间。从图2 可以看出，重庆、北京的合成效果较差，上海与合成上海在2010—2012 年呈现出了较明显的差异，其他3 个合成试点在干预前几乎产生了与真实值相同的曲线，由表2 中的估计误差可以得到类似的结果。

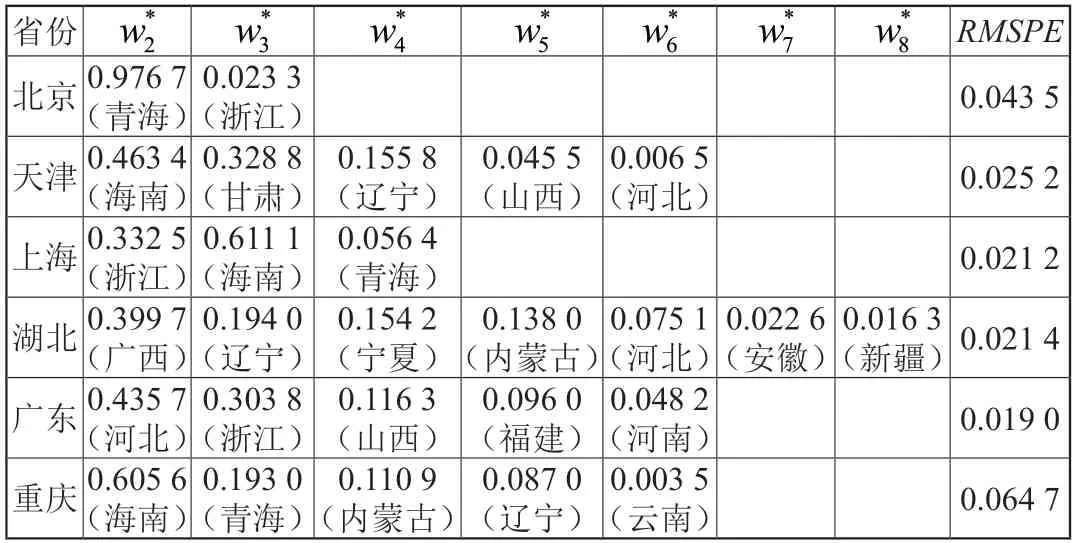
表2 2013年作为政策节点时各试点合成权重及估计误差

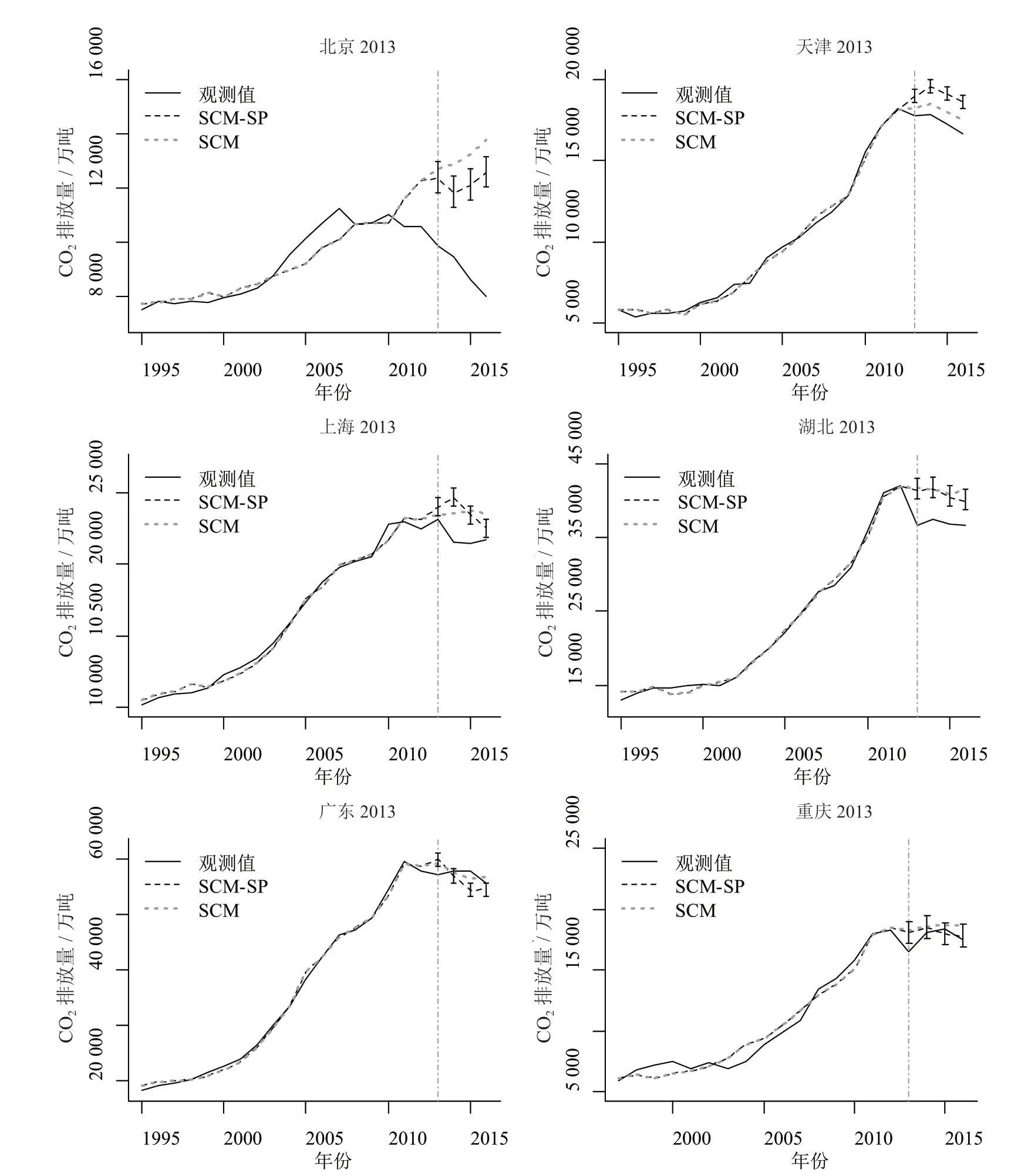
图2 试点地区CO2排放总量的观测值、SCM合成值、SCM-SP合成值及其95%置信区间

北京、天津、上海和湖北4 个试点的碳排放权交易政策均起到了显著的CO2减排效应，真实的排放总量与合成的相比在2013—2016 年间平均每年分别减少3221.88 万吨、1698.25 万吨、1686.00 万吨和3960.25万吨，约为以2012 年排放量作为基年的30.47%、9.33%、7.50%和9.43%，可见在减排总量以及趋势上仍呈现了明显的差异性。广东、重庆的合成值仅在2013 年显著高于真实值，但之后又出现政策效用变得不显著，而且广东甚至出现了负效用的现象。

SCM-SP 与SCM 得出的结果比较接近，得出的政策结论在方向上具备一致性，但在量上有所差异。以5%作为显著性水平，两种方法在天津的全部干预时期以及北京、上海和广东的部分时期存在显著性的差异，其中北京和广东传统的SCM 高估，而天津则低估了政策的干预效用，上海则同时存在低估和高估的时期，湖北、重庆由两种方法得到的结果不存在显著性差异。而具体未考虑溢出效应的后果与溢出结构的设定、合成权重均有关系，要通过稳健性检验来对结论的可靠性进行进一步的测量。

3.2 稳健性检验

为了检验以上碳排放权交易政策干预效用估计的可靠性，本部分分别从安慰剂、溢出矩阵设定和合成权重三个方面进行稳健性检验。

3.2.1 安慰剂检验

传统的安慰剂检验将每个控制单元依次看作实验单元，并为其估计反事实的CO2排放总量从而得到每个控制单元政策干预效应的估计，如果实验单元的干预效应显著高于控制单元则证明估计有效，这也称为“空间上的安慰剂（in-space placebos）”。Abadie 等[34]将安慰剂扩展到时间维度（in-time placebos），检测政策在时点设定上的稳健性。由于SCM-SP 给出了“空间上”的统计推断方法，因此本部分仅需进行“时间安慰剂”检验。将政策时点重新设定为试点颁布时期2011 年，若干预效应的估计值与2013 年相比显著变大，则有理由相信在2013年之前已经产生了效应，合成结果如图3 及表3 所示。

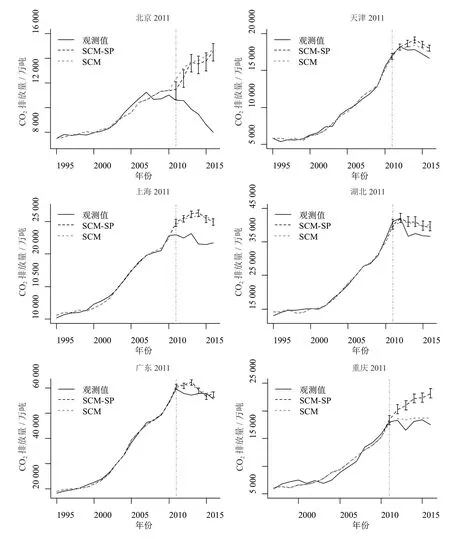
图3 试点地区CO2排放总量的观测值、SCM合成值、SCM-SP合成值及其95%置信区间

为了与2013 年作为政策节点进行对比，各试点纵向标度与图2 保持一致；表3 给出了此时的权重以及干预前预测误差。天津、湖北估计的预测误差升高，且在2011、2012 年未发生显著的政策作用，其中天津的干预效应大小与2013 年作为政策节点相比减小，因而以2013 年作为政策干预节点更可靠。北京、上海和广东的干预效应则较2013 年作为政策节点相比均提高，且在2013 年之前的合成省份与真实省份的CO2排放量也呈现了差异，估计误差降低，说明3 个试点以2011 年作为政策节点更可靠。重庆的预测误差与2013 年相比有较为明显的增加，因此将政策作用节点设定为2013 年较合理。

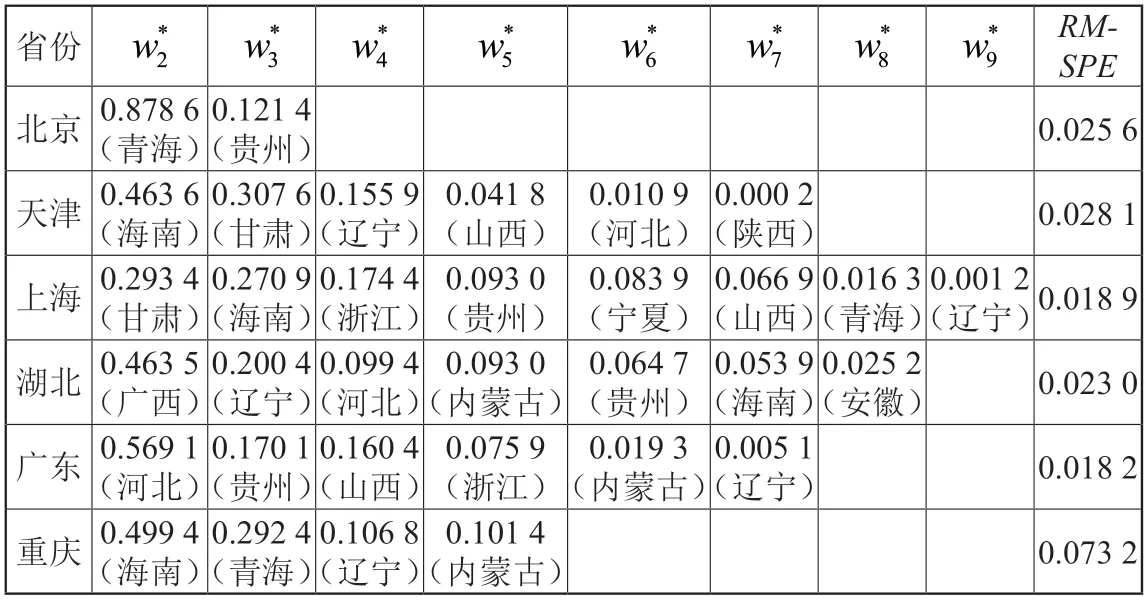
表3 2011年作为政策节点时各试点合成权重及估计误差

比较2011 年与2013 年作为政策节点的合成权重，同样得到天津、湖北的权重变化较小，其他省份权重变化较大。综上，将北京、上海和广东的政策干预年份看作2011 年，将天津、湖北和重庆的政策干预年份看作2013 年是合理的，说明碳排放权交易政策在不同地区起作用所需要的时间具有差异性。

3.2.2 溢出结构矩阵的稳健性检验

以安慰剂检验的结果为基础，得到不同权重下各个试点在干预时期的干预效用如图4 所示。溢出结构矩阵代表了政策溢出效用的空间结构，但在整个估计过程看作已知并且提前设定，然而当其无法描述正确的溢出结构时，有可能导致效用干预的偏误，因此估计效用对其设定的稳健性进行检验是必须的。将溢出结构重新设定为每个试点的二阶邻接矩阵A2，因此，北京、天津的溢出效应地区为河北、山东、内蒙古、辽宁、山西和河南6 个省份；上海的为江苏、浙江、山东、河南、福建、安徽和江西7 个省份；湖北的为安徽、江西、河南、湖南、陕西、江苏、浙江、福建、河北、山西、山东、广西、贵州、四川、内蒙古、甘肃和宁夏17 个省份；广东的为福建、江西、湖南、广西、浙江、安徽、贵州和云南8 个省份；重庆的为湖南、四川、贵州、陕西、江西、广西、云南、甘肃、青海、河南、山西、内蒙古和宁夏13 个省份。

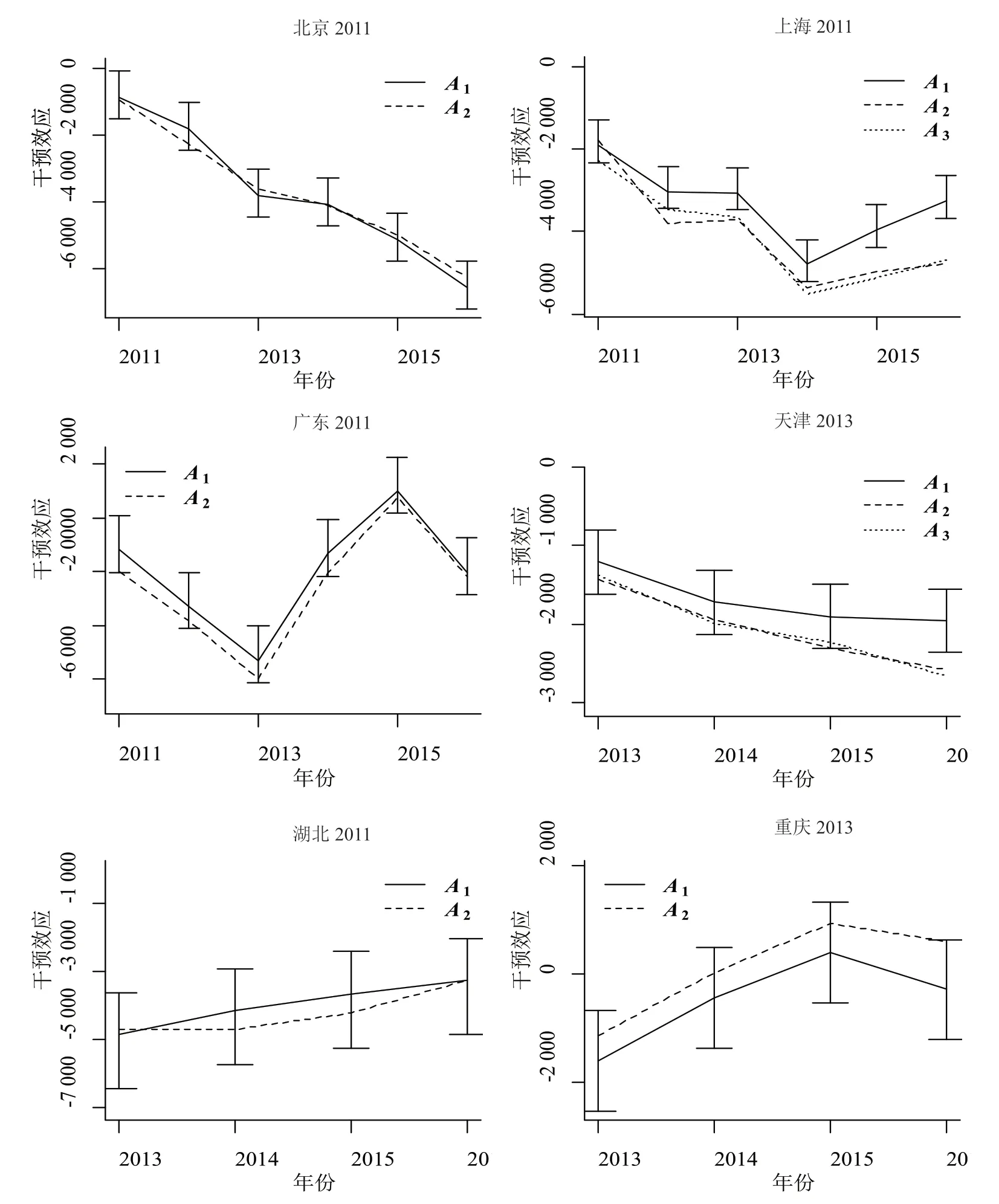
图4 政策干预效应对溢出权重结构的稳健性检验

由图4 可知，在两种溢出结构矩阵A1和A2的情况下均得到了相同的干预效应趋势，除了上海、天津在A2得到的干预效应在部分时期处于A1作为溢出结构5%的置信区间之外，其他地区的干预效应则具备一致性，因此为这两个试点再重新设定范围更广的溢出权重A3，并且得到了与A2近似的结果。由Cao &Dowd[28]可知，在溢出矩阵的设定高估溢出效应的时候，即设定的受溢出效应的个体比实际偏多时，估计量仍能保证较小的偏误程度，但是当溢出矩阵低估溢出效应时，估计量的偏误程度则会比较大。因此，将邻接矩阵设定A2的结果更加稳健。

3.2.3 合成权重检验

由表2 和表3 可知，每个试点均有权重较大的合成省份，那么干预效应是不是由于权重较大省份的趋势所造成的呢？因此有必要对合成权重的稳健性进行检验。以上两部分的检验最优结果为基础，将合成试点权重W*中大于0.1 的控制单元在每次迭代中依次从控制组中去掉，再估计每次迭代的干预效应[SCM-SP(LOO)]，排除干预效应是由于某一个控制单元的趋势所导致的可能性。

图5 展示了各个试点CO2排放总量观测值、合成值（黑色的实线、虚线）以及依次去除每个试点权重较大的控制单元的合成结果（灰色实线）。结果表明在去除控制单元前后，干预效应差异最大的是广东在合成控制单元中去除河北所得的结果，其中相差最多的为2013 年，与不去除相比下降了2.84%，因此干预效应估计结果对于从对照组中去除任意一个省份都是稳健的。

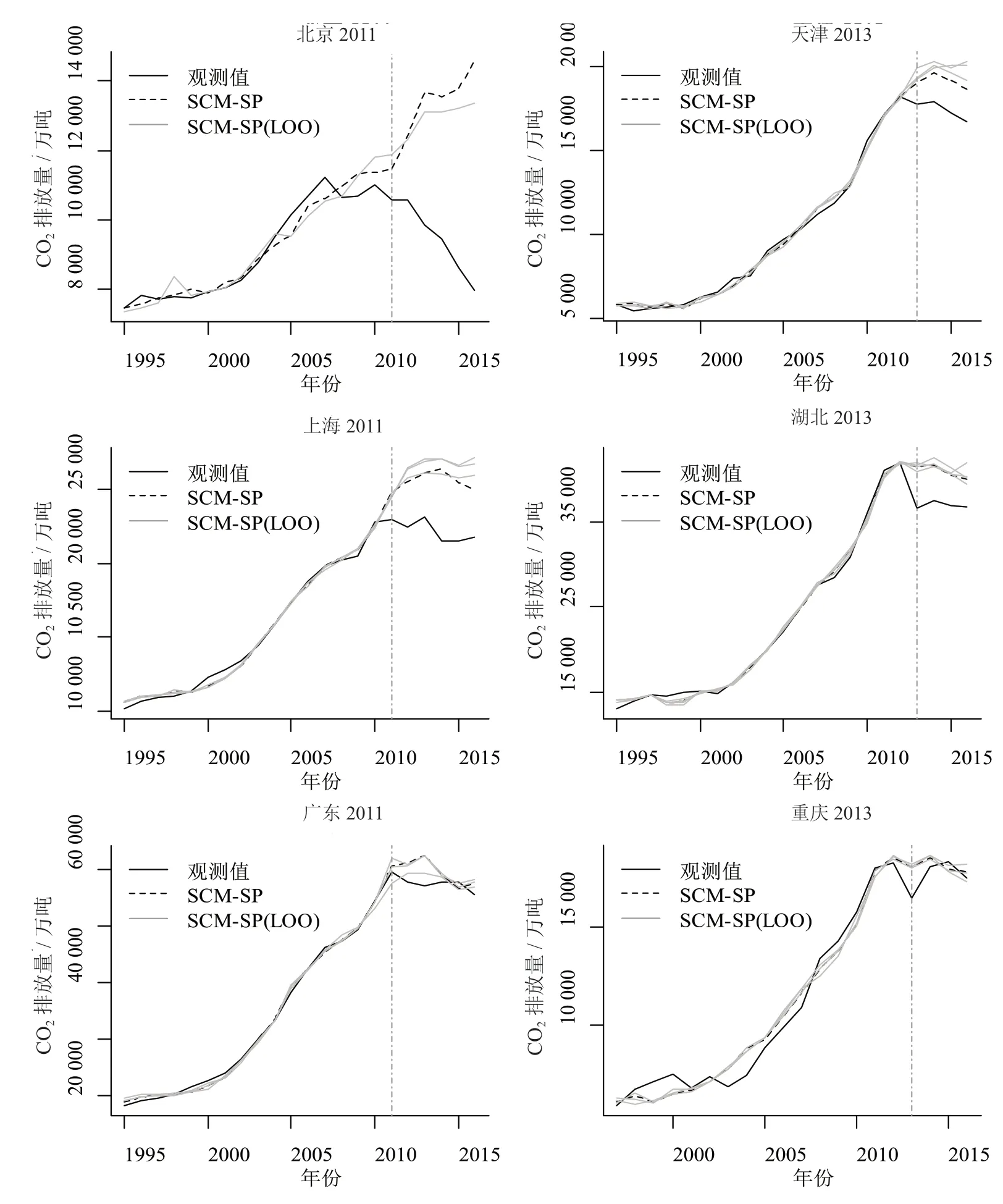
图5 政策干预效应对合成权重的稳健性检验

4 结论

本文在应用地区能源平衡表对各地区CO2排放量进行精确测量的基础上，将包含溢出效应的合成控制模型（SCM-SP）应用于分析碳排放权交易在试点地区的碳减排效应的研究，该方法在存在溢出效应以及近似政策存在的情况下仍能保证干预效应估计的准确性，适用于分析我国碳交易市场对碳减排效用的实际情况。SCM 与SCM-SP得到的政策作用方向具备一致性，但在量上存在差异，通过时间安慰剂检验、溢出矩阵设定检验以及合成权重检验为各试点碳交易的CO2减排效果进行了精确的定量分析。

研究发现，各试点的碳排放权交易在降低CO2排放效应方面存在显著的差异，无论是在作用时间以及作用大小方面，因此将各试点单独分析具有必要性。在效用时间上，北京、上海和广东在试点颁布后，即2011 年已经开始起作用，而天津、湖北和重庆是在2013 年开始交易时起作用；在碳减排程度上，各试点在各自政策的有效实施期间，CO2排放量分别平均每年下降了以政策节点前一年作为基年的33.87%、18.12%、3.71%、11.34%、9.43%和2.68%（试点排序与上述效用时间相同），其中2008年奥运会的举行是北京从2008年就开始下降的原因，其间大量高污染企业向外迁移[37]，因此也导致北京的碳排放权交易减排效用存在一定程度的高估。在政策持续性上，广东、重庆的碳交易市场对碳减排的持续效用较短，其他试点的政策在有效期内均有持续的碳减排效用。

此外，本文还探索了碳排放权交易政策对CO2排放强度（即单位实际GDP 所消耗的CO2）的干预效应，以探索CO2减排的作用机制，由于实证和检验过程与前文类似仅对结论进行阐述。在整个研究期内，所有试点的CO2排放强度均呈现大幅下降的趋势，但是除了湖北之外均不是由于碳交易市场的干预效应所致，这与沈洪涛等[19]得到的碳交易短期内通过降低微观企业的产量实现碳减排的结论一致。湖北作为最活跃的试点，更能够发挥碳交易的市场效用，促进资源更有效的配置，为其他试点以及全国碳交易市场设计提供有效的参考。